分數階黏彈性振子系統響應的代理模型分析

孫寶，張文超，李占龍，秦園，范凱

(1.太原科技大學應用科學學院，太原 030024；2.太原科技大學機械工程學院，太原 030024)

隨著國家經濟的不斷進步，科學技術的不斷發展，工程車輛已經普遍應用于工程應用中，為工程的實施帶來了便利。但是對于工程車輛來說，由于其本身工作環境的特殊性，使得其在特殊工況下工作時會產生劇烈的振動及噪聲，這不僅會對車輛的使用壽命有所損耗，還會對駕駛員的身心健康有所影響。研究表明，黏彈性材料作為阻尼所構建的黏彈性緩沖結構由于其廉價的制作成本和高效的減振緩沖能力，使得其被廣泛地應用于車輛的減振控制中，以達到更好的緩沖減振效果[1]。同時由于分數階建模優于整數階建模的非局部性，使得其僅需較少的本構參數就能更加準確的描述黏彈性材料的遺傳特性，能夠更好地反映黏彈性材料的力學特性。所以，分數階黏彈性建模被廣泛應用于工程車輛的研究中[2-3]。

隨著分數階微分建模的不斷發展，分數階微積分方程的解法也層出不窮。目前已有一些較為經典的解析解算法，如Laplace變換、Fourier變換等[4]。但是由于分數階黏彈性系統計算的復雜性，使得其解析解難以求得，因此對于分數階微分方程數值解的研究已成為學者們研究的熱點，常見的數值算法有：有限差分法[5]、譜方法[6]、正交多項式[7]逼近算法、Adomian分解法[8]和小波分析法[9]等。Ezz-Eldien[10]首次嘗試用譜方法求解FLPMs，結果表明：該方法能夠用較小的移位多項式獲得較高的精度。Mashali-Firouzi等[11]提出了一種用于求解非線性多項分數階初值問題的多步自適應偽譜方法，該方法求解精度高且適合大范圍的計算。Kim等[12]運用移位雅可比頻譜伽遼金法來求解分數階微分方程的初值問題，并驗證了多階線性和非線性分數階微積分方程解的收斂速度，但是求解過程較為繁瑣，在實際的工程問題中，需要耗費較高的成本。

近年來，數學模型與計算機模擬的結合已成為解決物理問題的方法之一[13]。但是由于計算機強大的模擬能力使得其運算成本較高，進而增大了實際工程中的成本預算。代理模型的出現很好地解決了這個問題，用代理模型或者元模型替代昂貴的工程問題，從而降低工程中的運算成本。代理模型是工程優化中常見的一種方法和手段，其思想是通過一定的方式和手段來處理優化過程中復雜的計算問題。代理模型具有較好的仿真模擬能力，被廣泛應用于各種工程問題中，包括優化設計、可靠性分析、基于可靠性分析的設計優化等[14]。

鑒于此，以標準性固體本構的分數階黏彈性振子(fractional viscoelastic oscillators of solid state constitutive, SFVEO)系統作為研究對象，首先給出一種基于分數階導數之間關系的數值差分格式，并分析在單位沖激激勵下系統參數對位移響應的影響。最后，為了解決分數階黏彈性系統優化計算的復雜性問題，用代理模型對系統的位移響應進行代理。研究成果可為分數階黏彈性振子系統響應分析及工程設計提供理論參考。

1 SFVEO模型建立及求解

1.1 SFVEO模型的建立

如圖1所示，SFVEO系統由兩個理想胡可彈性元k1、k2及分數階黏彈性元組成，其中，c為黏彈系數，α、β為分數階階次。分數階黏彈性元與彈簧k1為串聯結構，與彈簧k2為并聯結構。

σ、ε分別為黏彈性材料的應力和應變

黏彈性材料的分數階本構關系可表示為

Pσ=Qε

(1)

式(1)中：P、Q為表達黏彈性材料力學特性的分數階本構算子，其表達式分別為

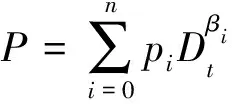
(2)

(3)

Caputo定義下的分數階微分算子，其定義為[15]

(4)

式(4)中：α為分數階階次；f(t)為求導函數；t為自變量；n為常數；Γ為Gamma函數；τ為中間變量。

取n=1,p0=1，p1=c/k1+k2，β0=0，β1=β，m=1，α0=0，α1=α，q0=k1k2/k1+k2，q1=k1c/k1+k2，則該黏彈性系統的本構關系為

σ+p1Dβσ=q0ε+q1Dαε

(5)

當系統在外界激勵的作用下，系統發生形變，為便于描述該系統的力學特性，現給系統外接一個質量為m的物體，如圖2所示，當系統受到的外部激勵所施加的力為f時，系統發生形變所產的阻尼力大小為fd。

圖2 SFVEO模型受力圖

根據經典振動力學方程有

(6)

(7)

由動力學方程得

(8)

式(8)中：l為該分數階黏彈性系統得長度；x為系統振動時外接物產生的位移。

將式(6)～式(8)代入式(5)中，并結合分數階微分算子的性質得

(9)

給定初值，將其轉化為數學模型為

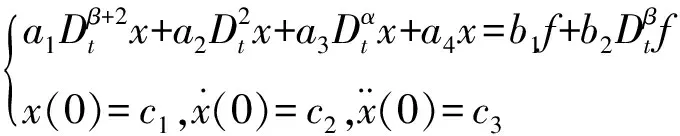
(10)

式(10)中：a1=p1；a2=1；a3=q1ζ/m；a4=q0ζ/m；b1=1/m；b2=p1/m；c1、c2、c3為常數。

1.2 SFVEO模型的求解

(11)

式(11)中：ωj為算術矩陣，無實際意義；j表示矩陣的行列數；h為步長；n=「α?，當初值為0時，分數階Caputo導數定義與分數階G-L導數相互等價。

用分數階G-L算子代替分數階Caputo算子，則方程的解為

(12)

式(12)中：Pn(x)為外界激勵和分數階導數項的非零初值項；(FM)t為外界激勵的零初值項。

2 單位沖激激勵下系統阻尼特性分析

當ξ=0.5，ζ=0.05，ωn1=ωn2=10，β=0.1時，分數階階次α變化對系統響應曲線的影響如圖3所示。

圖3 階次α變化對系統響應曲線的影響

當α取值小于0.5時，如圖3(b)所示，隨著α取值的不斷增大，響應曲線的第一幅值隨之減小，響應曲線的衰減速度不斷加快；當α取值大于0.5時，如圖3(c)所示，隨著α取值的不斷增大，響應曲線的衰減速度越來越快，但與圖3(b)相比，α取值越大，對系統的影響越不明顯。由圖3(a)可知，對于SFVEO模型，當調整模型參數時，會導致系統的響應曲線出現過阻尼的現象。

當ξ=0.5，ζ=0.05，ωn1=ωn2=10時，階次β變化對系統響應曲線的影響如圖4所示。由圖4可知，階次α和β的取值之間存在相互抑制的關系，當α=0.8時，β=0.5時出現過阻尼現象；當α=0.6時，β在0.4處就已經出現過阻尼現象。即α的取值越大時，β的取值范圍就越大。當階次α的取值固定時，隨著β取值的不斷增大，系統的振幅衰減速度逐漸減弱，且對系統位移響應影響較小。

圖4 階次β變化對系統響應曲線的影響

當ζ=0.05，ωn1=ωn2=10，α=0.7，β=0.2，阻尼比ξ=0、0.5、1時，系統響應曲線的變化如圖5所示。

圖5 阻尼比ξ=0、0.5、1時系統響應曲線的變化

隨著阻尼比取值的不斷增大，系統響應曲線的第一幅值呈下降趨勢，衰減速度不斷加快。

當ξ=0.5，ωn1=ωn2=10，α=0.7，β=0.2，幾何參數ζ=0.05、0.5、5時，系統響應曲線的變化如圖6所示。

圖6 幾何參數ζ=0.05、0.5、5時系統響應曲線的變化

單位沖激激勵下，隨著幾何參數的不斷增大，系統響應曲線的幅值較大，衰減速度較快。

當ξ=0.5，ζ=0.05，α=0.7，β=0.2，固有頻率ωn1=10、50、100，ωn2=10、50、100時，系統響應曲線的變化如圖7所示。

圖7 ωn1=10、50、100，ωn2=10、50、100時系統響應曲線的變化

當ωn1處于低頻狀態時，隨著ωn2的不斷增大，系統的衰減速度不斷增大，在低頻段，ωn2對系統響應曲線的幅值及衰減速度的影響較大。隨著ωn1取值的不斷增大，ωn2對系統響應曲線幅值及衰減速度的影響逐漸減小。當ωn1=10，ωn2處于低頻階段時，響應曲線衰減速度較快，當處于中頻或高頻階段時，系統響應曲線的第一幅值和衰減速度較為接近，對系統響應曲線影響較小。當ωn1和ωn2均處于中頻或高頻階段時，系統響應曲線衰減不明顯。

3 代理模型的構建

3.1 代理模型類型及構建流程

目前，常用的代理模型有Kriging模型、響應面模型、徑向基函數模型、正交多項式模型、支持向量回歸模型等。Kriging代理模型和響應面代理模型在處理復雜問題時計算時間短且精度高[16]，因此主要對這兩個模型進行介紹。

3.1.1 Kriging代理模型

Kriging模型是一種基于統計理論的插值模型，由向量x的多項式模型和向量x的局部偏差組合而成。該模型不僅能夠給出未知函數的預測值，還能給出預測值的誤差估計，其模型結構為

(13)

3.1.2 多項式響應面模型

多項式響應面模型是一種基于最小二乘法的多項式回歸模型，擬合結果能夠以顯示函數的形式表示出來，便于后續優化設計，且具有較好的連續性和可導性，使用非常便利。在多項式響應面模型中，若x是一個獨立因子向量，y為響應值，則存在式(14)所示的關系。

y=f(x)+e

(14)

式(14)中：e為均值為0、標準差為0的正態分布隨機誤差。

常用的模型有一次多項式響應面模型、二次多項式響應面模型、三次多項式響應面模型等。由于二次多項式響應面模型中無需較多的參數變量且變量間存在交互性，故被廣泛應用于求解實際工程問題，其模型表達式為

(15)

代理模型的優化過程大致分為試驗設計(design of experiment, DOE)、模型建立及優化分析3部分。其流程圖如圖8所示。

圖8 代理模型構建流程圖

由圖8可知，模型的建立步驟如下。

步驟1選取所研究系統的參數作為設計變量。

步驟2選取合適的試驗設計方法。

步驟3從系統中選取訓練樣本點和預測樣本點。

步驟4選擇代理模型。

步驟5通過訓練樣本的不斷訓練代理模型，生成訓練后的代理模型。

步驟6運用訓練后的代理模型預測出預測樣本點的預測值。

步驟7對預測樣本點的預測值與真實值進行誤差分析。

步驟8設置精度要求，若訓練后的代理模型達到了精度要求，則輸出最終的代理模型；若不符合精度要求，則返回步驟3，擴大樣本點的采點數量，從而繼續訓練代理模型，直至達到精度要求。

3.2 SFVEO系統代理模型的構建

依據代理模型構建步驟，現以SFVEO系統作為研究對象，進行代理模型的構建，構建具體過程如下。

3.2.1 設計變量的選取

設計變量的選取會直接影響優化問題的計算效率及精度，設計變量的數量過多或過少時都會影響代理過程的計算效率及精度。為了能較為準確的模擬出系統的位移響應函數，依據2節中地參數分析進行參數選取，階次β對系統位移響應反應不敏感，故選取系統頻率ωn∈[0,20]、阻尼比ξ∈[0,1]、分數階階次α∈[0,1]和幾何參數ζ∈[0,1]參數作為設計變量。

3.2.2 試驗方法的選取

選取拉丁超立方方法選取樣本點，在每個變量的取值范圍內選取訓練樣本點及測試樣本點。這里選取50個樣本點，且選用Kriging代理模型及二次多項式響應面模型進行代理計算，通過誤差分析，從而確定合適的代理模型形式。Kriging模型擬合效果如圖9所示。

圖9 Kriging模型擬合效果

借助計算機實驗的設計與分析(design and analysis of computer experiments，DACE)工具箱構建Kriging模型，設置初樣本點個數N為50，選取線性相關模型和二次多項式回歸模型，相關函數中的參數θ選取3.152，對SFVEO模型進行代理，當不滿足精度要求時選用加點策略，通過增加樣本點的個數來提高擬合精度。

由圖9可知，隨著樣本點數量的增加，擬合效果更為準確。同時，選用二次響應面模型對SFVEO進行代理，設置初始樣本點個數N為50，選用拉丁超立方設計選取樣本點。設置決定系數R2≥0.9時達到精度要求，兩種代理模型的誤差分析結果如表1所示。

表1 代理模型誤差分析對比

由表1可知，在選取較少樣本點時，二次響應面模型對SFVEO系統響應函數的代理效果更好，則輸出擬合后的SFVEO位移響應函數為

xS=0.009 18-0.000 20ωn1-0.000 14ωn2-

0.001 73ξ-0.001 72α-0.005 93ζ-

0.000 16α2+0.000 04ζ2-0.000 17ωn1ωn2-

0.000 24ωn1ξ-0.000 1ωn1α-0.001 5ωn1ζ-

0.002 42ωn2ξ+0.000 007ωn2α+0.000 01ωn2ζ+

0.000 97ξα+0.001 50ξζ+0.012 30αζ

(16)

綜上，相較于Kriging模型而言，二次響應面代理模型在選取少量的樣本點時就能對分數階黏彈性模型進行代理。

4 結論

以SFVEO系統作為研究對象，分析了其在單位沖激激勵下參數對系統動態響應的敏感程度，并選用Kriging模型和二次響應面模型對系統的響應函數進行代理，得出如下結論。

(1)α的取值對系統阻尼特性具有較大的影響，但是隨著α取值越大，對系統的影響越不明顯；β的取值對系統阻尼特性的影響較弱。

(2)隨著阻尼比和取值的增大，系統響應曲線的第一幅值呈下降趨勢，衰減速度不斷加快；隨著幾何參數ζ取值的增大，響應曲線衰減速度不斷加快。

(3)頻率ωn1和ωn2在低頻階段對系統阻尼特性的影響較大。當頻率ωn1處于高頻階段時，系統出現過阻尼現象。

(4)二次響應面代理模型對分數階黏彈性系統的代理效果優于Kriging模型。

系統的參數發生變化會導致系統出現過阻尼現象，實際的工程中為了避免這種現象所帶來的困擾，在實驗設計中需要對系統的剛度-阻尼參數進行優化。用二次響應面代理模型得到的結果可以用于后續的優化計算中，減少優化過程計算復雜度。