邊界載荷對層級橢圓穿孔板超材料帶隙的影響

張祖堅，郭 輝，王曉瑋，袁 濤，孫 裴

(上海工程技術大學機械與汽車工程學院，上海 201620)

0 引 言

機械超材料是一種人工周期性復合材料，在其帶隙范圍內可有效抑制彈性波的傳播，被廣泛應用于減振降噪[1-2]、超分辨率成像[3]、波濾波導[4]、水聲通信[5]等方面。

經研究發現，彈性波帶隙形成遵循Bragg散射機理[6-7]和局域共振機理[8]。隨著研究的深入，超材料結構由經典的桿、板、體等拓展到多孔結構。如Yao等[9]設計了一種周期性“框架-彈簧-質量”系統，即典型的局域共振單元，該結構可用于制作隔振板。Wang等[10-11]研究了不同孔型的聲子晶體帶隙特性，其中“十”字孔結構的二維聲子晶體具有多個完全帶隙。Krushynska等[12]設計的由單一材料組成的具有準共振Bragg帶隙超材料，其帶隙寬度和位置均能保持穩定。而Tian等[13]在相互正交的矩形穿孔板中加入了4個螺旋孔，使得該結構可同時打開Bragg和局域共振帶隙。

為適應各類復雜場景應用需求，研究人員一直致力于探索超材料帶隙的調控方法，如改變原胞結構幾何參數、對其拓撲優化以及引入層級結構等以調控超材料帶隙位置、寬度等，但至今仍存在諸多挑戰。因此，Sun等[14-15]采用改進的遺傳算法優化了蜂窩結構中的材料分布，可有效拓寬帶隙寬度和調控帶隙中心頻率位置。Sepehri等[16]設計了蛛網和雪花狀的層級結構，可實現對六角形和三角形超材料局域共振帶隙的調控。Miniaci等[17]設計了輪輻層級結構和十字形層級多孔超材料結構，發現層級結構在明顯減小整體結構重量的同時，可額外產生更低頻率的帶隙。Billon等[18]通過在層級矩形板中嵌入穿孔結構，并拓撲形成一種新型超材料，在該結構產生較寬帶隙的同時，帶隙向低頻范圍移動；Xu等[19]設計了包含局域共振單元的層級超材料結構，該結構可將各帶隙范圍的彈性波有效衰減。

然而，盡管上述帶隙調控手段是有效的，但忽略了超材料結構在實際應用時的受載情況，僅通過引入層級的方式設計超材料結構仍存在一定局限性。因此，Bertoldi等[20-22]通過對其制作的超材料結構施加外部載荷誘導出多種模式的屈曲變形，從而改變該結構的帶隙特性，這為彈性波調控提供了新的思路。Shim等[23-24]針對4種周期性多孔平面結構研究了在單軸壓縮載荷作用下彈性波的傳播特點，實現了通過單軸張力調控泊松比和彈性波帶隙的目的。此外，孔型的排列方式也會造成結構屈曲變形及相應的模態變化[25-29]，Li等[30-31]對軟多孔結構采用不同方式填充鋼柱，研究結構在單軸載荷作用時屈曲變形對帶隙特性的影響，得到了低頻可調控的帶隙。Dudek等[32]提出了新的二維和三維微尺度的層級機械超材料，研究發現，改變連接元件的鉸鏈厚度時，該結構能表現出可控的拉脹行為。

可見，施加外部載荷是調控多孔層級超材料帶隙的一種途徑，目前對穿孔結構施加載荷作用的研究主要集中于力學性能方面。而與方形和圓形穿孔板結構相比，橢圓穿孔板更易于打開帶隙，不同層級間孔型的分布方式更加多樣化，且載荷引起的結構變形可調控帶隙分布。本文基于橢圓穿孔板結構[33]建立3個層級橢圓穿孔板模型，通過對不同層級結構的邊界施加載荷，研究不同載荷與帶隙的分布規律，以期得到更多的完全帶隙和方向帶隙。

1 彈性波理論

彈性波在超材料結構中傳播時，受其內部周期性結構作用而形成特殊的色散關系，為表征該特殊色散關系，本文采用商用軟件COMSOL Multiphysics進行了本征頻率計算分析。通過求解平衡方程，可得到頻率f和波矢k的變化曲線，即能帶結構。彈性波在晶格特性的周期介質中傳播時，其波動方程如公式(1)所示：

(1)

(2)

根據Bloch定理可將位移用公式(3)表示：

u(r,t)=uk(r)ei(k·r-ωt)

(3)

式中：k為波矢；uk是與各材料參數具有相同周期的函數。采用有限元法計算，對于任意離散單元可得到公式(4)：

(K-ω2M)u=0

(4)

式中:K為結構全局剛度矩陣;M是結構全局質量矩陣;u是特征向量;ω為結構振動頻率。

2 層級橢圓穿孔板超材料模型

本文設計的橢圓穿孔板結構分為三個不同層級，不同層級的幾何參數通過公式(5)～(7)進行定義。其中，ai表示第i層級原胞尺寸，bi表示第i層級橢圓長半軸長度，ci表示第i層級橢圓短半軸長度，它們均按照下一層級與上一層級的比例來設定。該結構中，填充的圓柱體半徑R=0.2ai，圖1為第一層級橢圓穿孔板結構(左側)和原胞模型(右側)。

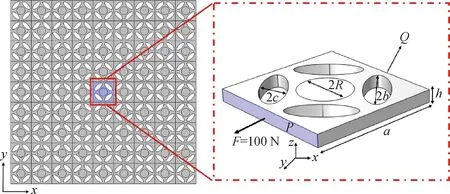
圖1 橢圓穿孔板模型

(5)

(6)

(7)

上述結構中基體為尼龍，材料參數為彈性模量E0=1.8×109Pa、密度ρ0=1 010 kg/m3、泊松比ν0=0.38，中間填充體為銅質圓柱，材料參數為彈性模量E1=1.64×1011Pa、密度ρ1=8 950 kg/m3、泊松比ν1=0.34。第一層級中原胞結構的尺寸為40 mm×40 mm×10 mm，包覆的銅質圓柱塊高h=10 mm，半徑R=8 mm，第一層級結構幾何參數如表1所示。

表1 原胞結構幾何參數

根據文獻[34]，在有限元計算中，掃掠相同布里淵區時可將高度在0.1a～0.5a的三維結構簡化為二維平面結構進行計算。本文將高度為0.25a的三維結構簡化為二維平面結構，以便于研究其面內帶隙特性。根據表1和各材料參數建立了不同層級橢圓穿孔板模型，如圖2所示。

3 邊界載荷對帶隙的影響

基于彈性波理論和有限元法計算出各層級的能帶結構及相應振型，考慮到精確度和計算效率，只研究前20階振型，與之對應的為前20條能帶。為方便觀察帶隙頻率與材料參數、結構參數之間的關系，將能帶結構圖的縱坐標數值通過公式(8)進行歸一化處理。

(8)

式中：Ω為歸一化頻率；f為頻率；a為晶格常數；ct為橫波波速。

根據結構是否受邊界載荷作用，分別用Ⅰ、Ⅱ和Ⅲ表示無邊界載荷作用的第一、第二、第三層級結構，用Ⅰ0、Ⅱ0和Ⅲ0分別表示有邊界載荷作用的第一、第二、第三層級結構，如表2所示。

表2 層級結構的序列

在對比分析能帶結構和振型時，按照表2將相鄰層級分為4組：層級Ⅰ和層級Ⅱ、層級Ⅱ和層級Ⅲ、層級Ⅰ0和層級Ⅱ0、層級Ⅱ0和層級Ⅲ0。將層級結構有無邊界載荷作用分為3組：層級Ⅰ和層級Ⅰ0、層級Ⅱ和層級Ⅱ0、層級Ⅲ和層級Ⅲ0。

3.1 無邊界載荷時帶隙計算和分析

計算得到的層級Ⅰ能帶結構和傳輸損耗分別如圖3(a)、(b)所示，其中灰色陰影部分表示完全帶隙，黑色陰影部分表示XM方向帶隙。從圖3(a)可知，層級Ⅰ在前20條能帶共打開了3個完全帶隙和3個XM方向帶隙，其中第一個完全帶隙范圍為0.60～0.70，分布在第5、6能帶之間；第二個完全帶隙同時也是帶寬最大的帶隙分布于第6、7能帶之間，范圍是0.75～1.0。從圖3(b)可知，傳輸損耗系數在3個完全帶隙范圍內大幅下降，3個方向帶隙范圍也均有不同程度的下降。

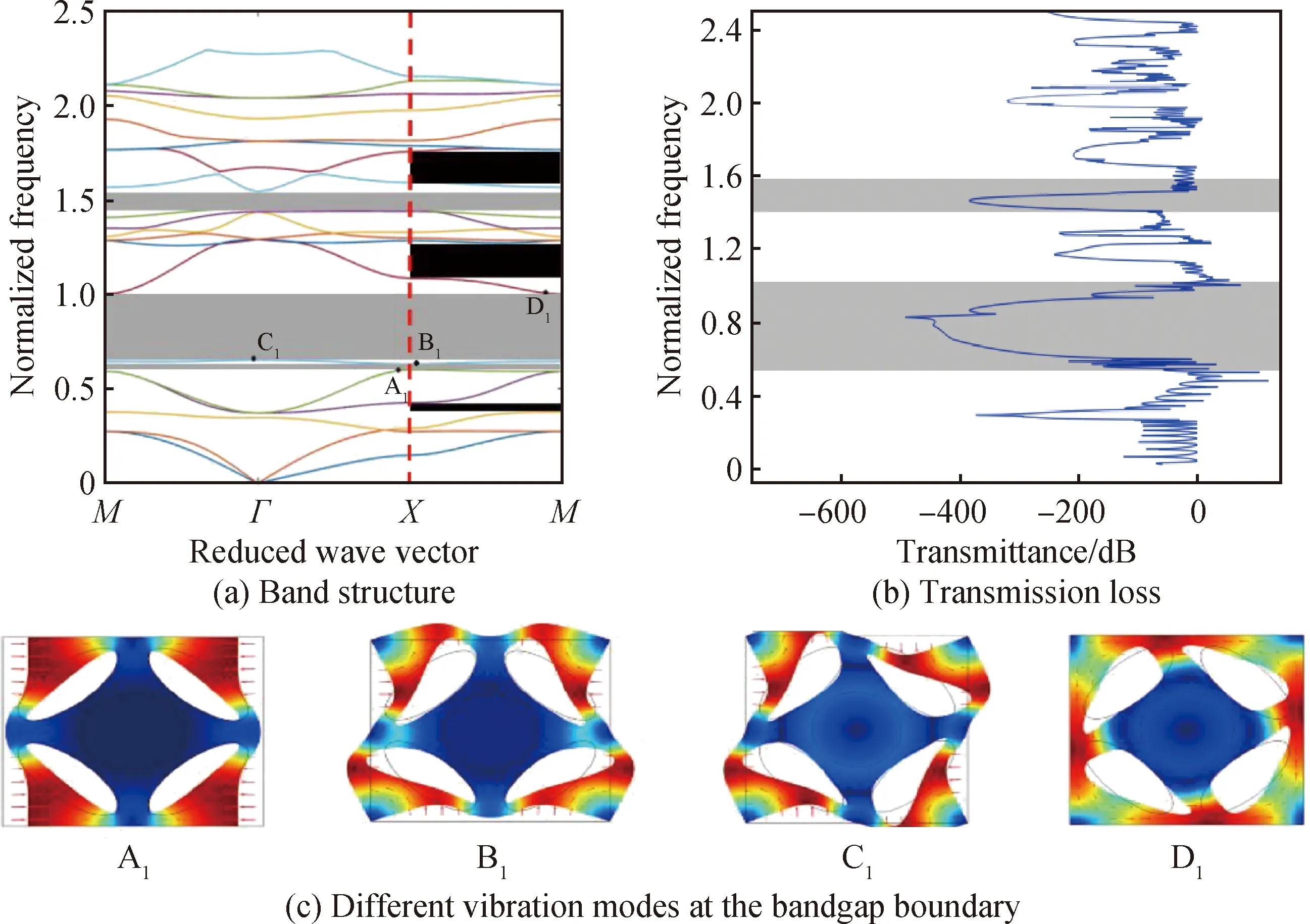
圖3 層級Ⅰ的帶隙特性和振型

圖3(c)對應圖3(a)中第一個完全帶隙和最寬帶隙上、下邊界處的振型。由圖3(c)中的A1知，該結構四個角部分可等效為局域振子，彈性波傳播過程中的能量在該區域被耗散，帶隙開始打開。圖3(c)中的B1顯示，此時該結構四周邊界圍繞四個角振動，而結構中心基本保持靜止，彈性波隨著結構邊界的振動繼續傳播，帶隙關閉。圖3(c)中的C1表明，此時該結構四個角部分圍繞四個角旋轉振動，且結構中心填充的銅質圓柱體開始小幅度振動，該部分也可視為局域振動，起到衰減彈性波的作用并打開帶隙。從圖3(c)中的D1可知，該結構四周邊界圍繞結構中心逆時針旋轉振動，且以邊界中心韌帶處振動最為激烈，彈性波繼續傳播，帶隙關閉。

層級Ⅱ共有2個完全帶隙和4個XM方向帶隙，如圖4(a)所示。第一個完全帶隙分布在第4、5能帶間，范圍為0.25～0.35；第2個完全帶隙分布于第18、19能帶間，范圍為1.05～1.3。從圖4(b)可知，傳輸損耗系數在2個完全帶隙范圍內大幅下降，并在4個方向帶隙范圍有不同程度的下降。

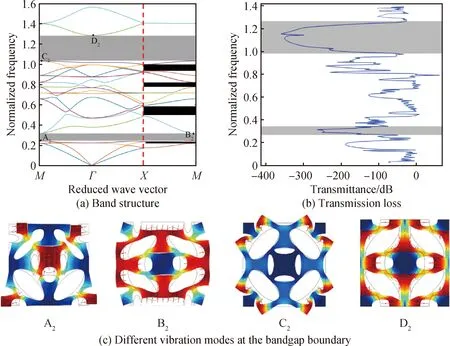
圖4 層級Ⅱ的帶隙特性和振型

從圖4(c)中A2可知，該結構四個角沿著特定方向振動，而結構中心填充的銅質圓柱體沿著y方向振動，該部分振動可等效為局域振動，衰減彈性波的傳播，第1個完全帶隙由此打開。當第1個完全帶隙關閉時，圖4(c)中B2和帶隙打開時A2相反，B2中該結構四個角和中心位置均保持靜止，而結構邊界和韌帶沿著特定方向振動。由圖4(c)中C2可知，最寬帶隙打開時，該結構的四個角、韌帶和中心位置均為靜止狀態，而結構邊界振動部分可等效為多個局域振子，從而對彈性波的傳播進行衰減。從圖4(c)中D2可知，該結構的四周邊界和中間韌帶位置劇烈振動，彈性波在該結構中繼續傳播，帶隙關閉。

層級Ⅲ的能帶結構和傳輸損耗分別如圖5(a)、(b)所示。從圖5(a)可知，層級Ⅲ只有1個完全帶隙和3個XM方向帶隙，完全帶隙分布于第18、19能帶間，范圍是0.95～1.11，在Ω=1附近層級Ⅲ的帶寬比層級Ⅰ和層級Ⅱ都小。從圖5(b)可知，彈性波不僅在完全帶隙范圍內被大幅度衰減，在3個方向帶隙范圍內也有不同程度的衰減。

從圖5(c)的A3可知，該結構的四個角產生局域共振，在歸一化頻率Ω=0.95附近，彈性波因局域共振作用而不能通過該結構，因此帶隙開始形成。從圖5(c)中的B3可知，連接該結構中心的韌帶和連接該結構四個角位置的韌帶劇烈振動。這是因為層級的增加導致韌帶幾何尺寸減小，使得該結構整體等效剛度減小，而添加的銅質圓柱體難以減弱結構對幾何缺陷態的敏感性，導致結構在該頻率下劇烈振動，從而帶隙消失。

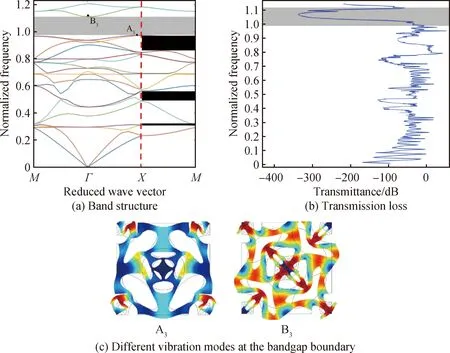
圖5 層級Ⅲ的帶隙特性和振型

通過比較層級Ⅰ、Ⅱ、Ⅲ的能帶結構可知，在層級增加的過程中，完全帶隙數量逐漸減少，且在Ω≤1范圍內的完全帶隙逐漸消失。由此可知，能帶結構會因層級的增加而發生變化。

3.2 有邊界載荷的帶隙計算和分析

載荷引起的結構變形可有效改善帶隙特性，為探索載荷對超材料帶隙的影響，以第一層級結構為例，在材料的完全線彈性范圍內，對不同層級結構施加邊界載荷并計算其能帶結構，此處邊界載荷是指在P邊界面施加的100 N均勻恒定載荷，如圖1(b)所示。在該結構邊界受到單軸載荷作用后，為防止發生位移，把Q面的邊界條件設為固定約束。

層級Ⅰ0的能帶結構和傳輸損耗分別如圖6(a)、(b)所示。從圖6(a)可知，層級Ⅰ0共有9個完全帶隙和6個XM方向帶隙，其中第一個完全帶隙范圍為0.25～0.40，分布于第2、3能帶間，帶寬最大的帶隙為0.61～0.97，分布于第7、8能帶間。從圖6(b)傳輸損耗曲線可知，彈性波在9個完全帶隙和6個方向帶隙范圍內被大幅度衰減。

圖6 層級Ⅰ0的帶隙特性和振型

根據圖6(c)的A01可知，該結構上方兩角部分可等效為局域質量產生局域共振，彈性波因結構的局域振動被衰減，開始形成帶隙。由圖6(c)中B01可知，結構中心的圓柱體向水平方向振動，該結構上方左右兩側振動方向則相反，當彈性波大于結構本征頻率時，結構的局域振動不足以衰減彈性波，帶隙消失。從圖6(c)中的C01可知，它與A01不同的是，該結構上方的邊界沿著外側方向發生局部共振從而形成帶隙。而從圖6(c)中D01可知，因結構的上邊界與連接中心質量塊的韌帶部分有著不同方向的振動，局域共振的作用不足以衰減彈性波傳播，此時帶隙消失。從圖6(a)可知，帶隙開始形成時能帶大多呈平直狀態，且圖6(b)中傳輸損耗系數在帶隙范圍內明顯下降，說明彈性波明顯被局域共振所衰減。

層級Ⅱ0共打開了10個完全帶隙和7個XM方向帶隙，其中第一個完全帶隙范圍為0.13～0.15，分布于第1、2能帶間，帶寬最大的帶隙為1.08～1.37，分布于第18、19能帶間，如圖7(a)所示。傳輸損耗系數在10個完全帶隙和7個方向帶隙范圍內大幅下降，表明彈性波在相關帶隙范圍內可被有效衰減，如圖7(b)所示。

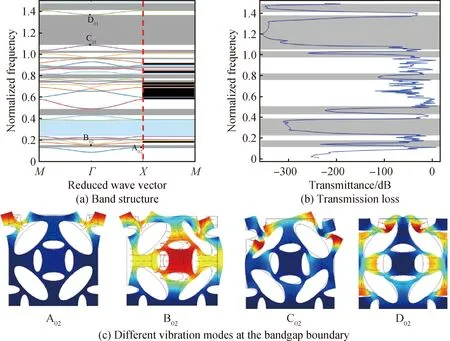
圖7 層級Ⅱ0的帶隙特性和振型

從圖7(c)中的A02可知，該結構上方兩角的局部質量沿著特定方向振動，彈性波在傳播過程中的能量被局域振動衰減，從圖7(a)可知，第一個完全帶隙打開時能帶非常平直，因此說明該結構對彈性波群速度有明顯的衰減作用。圖7(c)中B02的振動模式和B01類似，振動發生在結構中心和韌帶位置，以及結構上方的兩角，當彈性波頻率大于該結構的本征頻率時，因局域共振的作用逐漸減弱，彈性波隨著結構的振動繼續傳播，導致帶隙關閉。對于圖7(c)中C02，由于引入層級導致結構內部邊界數量增加，彈性波在該周期結構中傳播時，部分彈性波在結構內部的邊界發生反射，與入射的行波發生相互作用，從而產生布拉格帶隙。從圖7(c)中D02可知，該結構下邊界因施加固定約束保持靜止，而其余邊界和左右兩側的韌帶振動模式與圖5(c)中D2類似，彈性波因結構的振動向下一個周期單元繼續傳播，因此帶隙消失。

層級Ⅲ0的能帶結構和傳輸損耗曲線如圖8(a)、(b)所示。從圖8(a)可知，層級Ⅲ0共有11個完全帶隙和6個XM方向帶隙，其中第一個完全帶隙為0.18～0.20，分布于第1、2能帶間，帶寬最大的帶隙為1.01～1.16，分布于第18、19能帶間。從圖8(b)中傳輸損耗系數大幅下降可知，彈性波在11個完全帶隙和6個方向帶隙范圍內均被有效衰減。

圖8(c)中A03振動模式和圖7(c)的A02相同，只有作為局部質量的兩角位置發生振動，彈性波因局域振動被衰減。圖8(c)中B03的振型和圖8(c)中B02類似，在結構的中心和上方角位置處產生振動，彈性波隨著結構振動繼續傳播。由圖8(c)中C03和D03振型可知，當彈性波在傳播過程中引起結構振動，因入射波和反射波相互作用，從而打開帶隙；當反射波的頻率、相位和入射波不同時，布拉格散射作用減弱直至消失，帶隙隨之關閉。

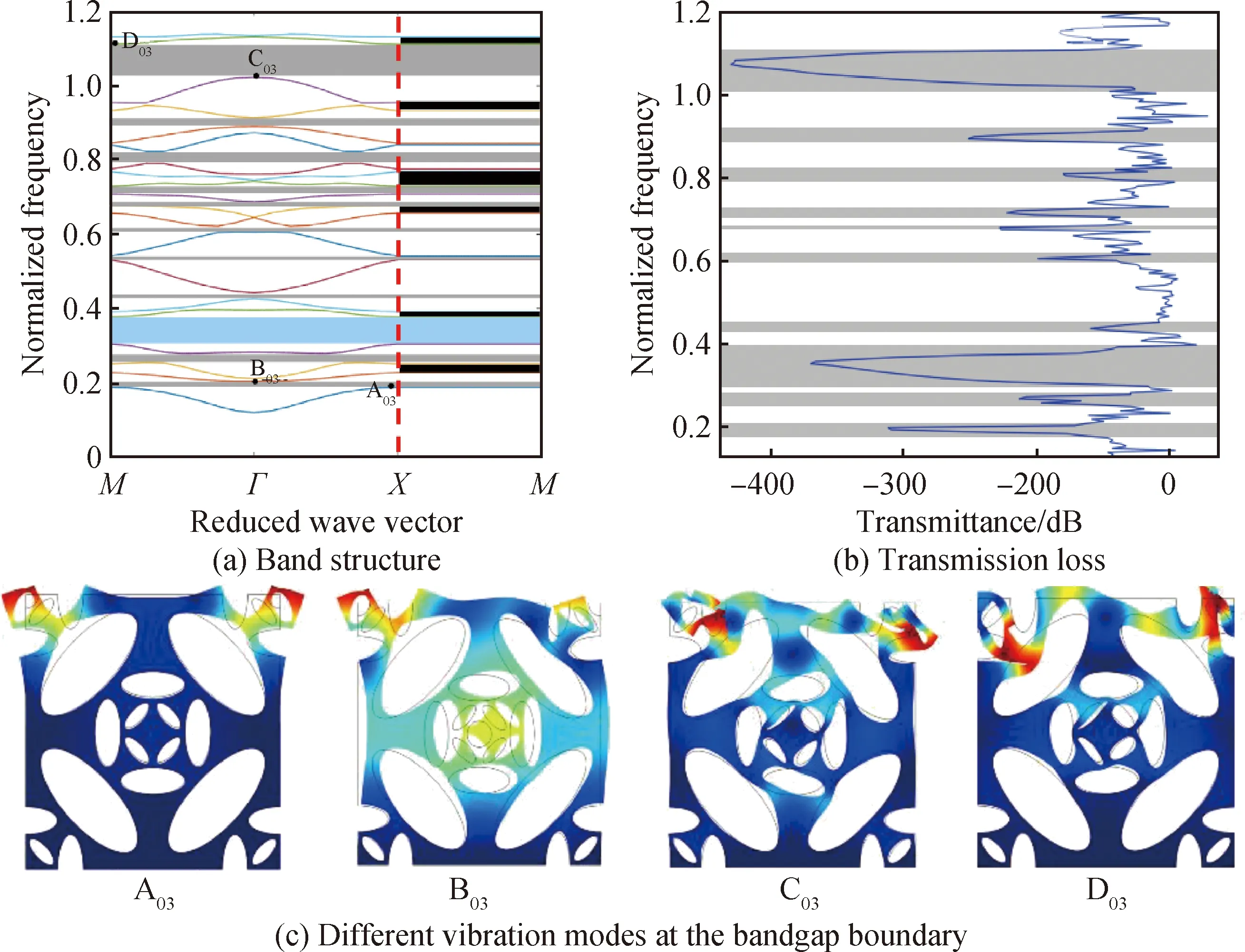
圖8 層級Ⅲ0的帶隙特性和振型

根據上述分析可知，邊界載荷引起的結構變形可改變其本征頻率，并可將簡并態能帶打開形成帶隙。以層級Ⅱ、層級Ⅲ的第5、6條能帶為例，由圖4(a)、圖5(a)可知，無載荷作用時第5、6條能帶在X點發生“簡并”，即在X點處彈性波能量相同但對應兩個不同的本征頻率。在施加載荷作用后，由圖7(a)、圖8(a)可知，第5、6條能帶簡并態消失從而形成帶隙，同時在其他XM方向打開了多個方向帶隙。

另外，由圖2可知層級的增加造成結構邊界面的橫截面積減小，以及結構內韌帶部分幾何尺寸減小，導致結構整體等效剛度減小，因此結構本征頻率下降。若用ωn+1、ωn分別表示第n(n≤19)個帶隙上、下邊界的頻率，ωc=(ωn+1-ωn)/2表示帶隙中心頻率，由圖6(a)、圖7(a)和圖8(a)可知，總體上帶隙中心頻率均下降。而在施加載荷作用后，層級Ⅰ0、層級Ⅱ0和層級Ⅲ0打開的完全帶隙數量明顯增多；在Ω≤1范圍內，層級Ⅱ0、Ⅲ0最寬帶隙如圖7(a)和圖8(a)藍色陰影部分所示，很明顯，隨著層級的增加該范圍內最寬帶隙的帶寬在逐漸減小。從圖6(b)、圖7(b)和圖8(b)的傳輸特性曲線可知，在帶隙范圍內傳輸損耗系數均小于-150 dB，說明對該結構施加載荷作用可有效衰減彈性波的傳播。

圖9表示第一層級結構的帶隙在不同邊界載荷作用下的變化，從圖中可知，在載荷增大的過程中，完全帶隙的數量在逐漸減少。另外，在載荷增大的過程中，帶隙上邊界的頻率幾乎不變，而帶隙下邊界的頻率則不斷增大，因此第一個完全帶隙和最寬帶隙的帶寬隨著載荷的增大而逐漸減小。通過上述結果可知，合理施加邊界載荷，可改善帶隙特性。

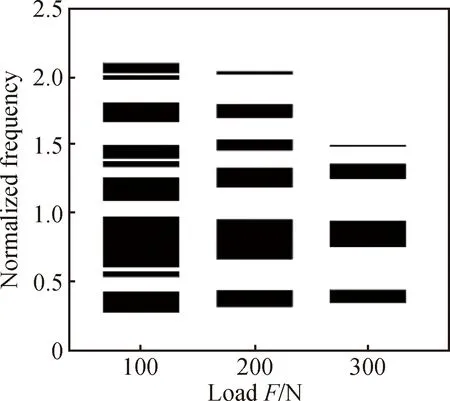
圖9 帶隙寬度隨不同邊界載荷的變化關系

4 結 論

通過研究不同層級橢圓穿孔板超材料在有無邊界載荷情況下的帶隙特性、傳輸損耗及相關振型變化，發現在結構邊界施加載荷后可使能帶結構和振型發生明顯變化，從而得出以下結論：

1)在結構不考慮邊界載荷作用的影響時，通過引入層級設計，增加層級數量可降低帶隙的頻率，實現對低頻彈性波的有效抑制。

2)在考慮邊界施加載荷作用的影響時，層級橢圓穿孔板結構的簡并態能帶被打開且“拉直”成平帶，可打開更多的方向帶隙及增大方向帶隙的帶寬，有利于在更寬頻率范圍內抑制特定方向的彈性波傳播。

3)在超材料結構的多個區域形成局域振子，可增加彈性波傳播過程中的能量耗散。引入層級設計并施加一定邊界載荷是抑制彈性波傳播的有效途徑。

值得說明的是，不同邊界載荷對超材料結構力學性能及帶隙特性的影響程度不同，本文研究僅限于完全線彈性變形階段，因此，多種類型的載荷作用情況下超材料結構的剛度和泊松比的變化情況值得進一步研究討論。此外，還可采用合適的拓撲優化方法來拓寬低頻范圍的帶隙寬度，以便于實際工程應用。