考慮動態曲線特征的退役鋰離子電池分選方法

聶金泉，黃燕琴，高洋洋，李銀銀，王聃軻

(1.湖北文理學院 汽車與交通工程學院， 湖北 襄陽 441053；2.純電動汽車動力系統設計與測試湖北省重點實驗室， 湖北 襄陽 441053；3.襄陽市公共檢驗檢測中心， 湖北 襄陽 441000)

0 引言

鋰離子電池(lithium-ion battery,LIB)具有能量密度高、循環壽命長、無記憶效應等優點，已廣泛應用于電動汽車和儲能等領域[1]。自2021年，我國開始迎來第一批動力電池退役高峰期。退役電池如何處理成為新能源汽車產業迫在眉睫的發展難題。將其規模化應用于儲能系統是解決該問題的有效途徑[2-3]。考慮到電池組的最大可用容量主要由可用容量最小的電池決定[4]，且越來越多的安全事故開始引起人們對于鋰離子電池安全問題的思考[5]。因此，需要通過合理的分選方法延長電池的循環使用壽命，減少安全問題[6-7]。

國內外學者針對退役電池分選技術已經展開了大量研究[8-10]，主要從提高分選效率和分選精度兩大方向入手。Lai等[11]和鄭岳久等[12]提出了采用電壓快速預估容量的方法；Lai等[13]提出了基于融合算法進行容量內阻快速分選的方法。殷娟娟等[14]利用層次聚類分析和最小二乘原理建立了一套關于鋰電池快速評價分選的流程，該方法最多只需要進行一次放電。張瑛[15]基于GA-BP神經網絡算法訓練健康狀態估計模型，該方法在不同工況及不同電池種類的最大誤差均小于2%，平均絕對誤差及均方根誤差小于1.5%。 駱凡等[16]提出了一種基于短時脈沖放電與電化學阻抗譜(EIS)相結合的退役電池快速分選方法，能有效降低能耗，有較大的實用價值。上述方法實現了對退役電池的快速分選，但一致性有待進一步提高。薛金花等[17]提出了基于老化機理分析的分選方法，分選出的電池組成的電池組在電池組容量利用率和溫度一致性方面都具有較好的效果。楊超等[18]通過固定電壓窗口的方法得到放電平臺高度及長度數據，該方法能顯著降低電池模組的不一致性。Liao等[19]通過容量測試、脈沖測試和電化學阻抗譜測試完成了一致性分選。王帥等[20]提出了多參數與動態電壓分選相結合的方法，提高了退役電池模組的一致性。

為了提高退役電池的一致性，運用充電能量與放電能量之差表述一般測試過程中的化學極化和濃差極化等。通過多參數預分選，結合電壓曲線和能量曲線動態分選的方法提高電池能量利用率，延長鋰電池的循環使用壽命。同時，提出通過頻率分布直方圖和頻率分布曲線分析確定K-means算法的K值，以解決K-means算法K值不確定的問題。

1 鋰離子電池性能測試過程

1.1 測試設備

考慮溫度對電池充放電過程中參數的影響，采用新威BTS 7.6.X電池綜合測試系統，KCS-8900B可程式恒溫恒濕試驗箱，裝載試驗所需軟件的上位機和單體鋰離子電池搭建試驗平臺進行電池充放電測試。采用日置HIOKI BT3562內阻測試儀進行電池內阻和電壓的測試。BTS 7.6.X電池綜合測試系統擁有16通道。KCS-8900B可程式恒溫恒濕試驗箱溫度波動度為±0.5 ℃。HIOKI BT3562內阻測試儀內阻測量精度為±0.5%，電壓測量精度為±0.01%。實驗平臺實物見圖1。

圖1 實驗平臺實物

1.2 測試指標

1.2.1容量

文獻[6]的研究表明電池組的容量比單體電池中的最小容量更低。電池組容量由所有單體電池中當前可放電最小電量和可充電最小電量的電池決定。

1.2.2內阻

電池的內阻直接影響電池外在參數差異。在循環充放電過程中，各單體內阻大小可反映單體間的一致性。所有單體內阻分布越集中，其一致性越好；反之，越分散則一致性越差。

1.2.3能量

考慮到充放電過程中，電池內阻和連接件內阻會消耗部分電能，Li+嵌脫的電化學極化和濃差極化也會導致部分能量損失，因此，可采用充電能量與放電能量之差表述電池的這種差異來描述一般測試過程中的化學極化和濃差極化等。

1.2.4電壓

為了防止電池過充過放，最高的單體電池電壓達到充電截止電壓時整個電池組停止充電；放電時，當最低的單體電池電壓達到放電截止電壓時停止放電。

根據電池不一致性的表現形式，確定放電容量、充電電壓、放電電壓、能量差、充電內阻、放電內阻6個參數作為多參數的分選指標。其中，放電容量為電池在標準充放電條件下的充放電容量，用Q表示,單位為Ah；充放電電壓為電池在標準充放電條件下充滿和放完電時的電壓值，分別用U1和U2表示,單位為V；能量差為電池在25 ℃標準充放電條件下充電能量與放電能量之差，用E表示，單位為Wh；充放電內阻為電池在標準充放電條件下充滿和放完電時的內阻值，分別用R1和R2表示,單位為mΩ。

1.3 測試方法及數據

充放電流程參考GB/T31486—2015《電動汽車用動力蓄電池電性能要求及試驗方法》、GB/T31467.2—2015《電動汽車用鋰離子動力蓄電池包和系統第2分：高能量應用測試規程》，具體步驟：① 以2 A恒流放電至3 V；② 擱置1 h；③ 以2 A恒流恒壓充電至4.2 V；④ 擱置1 h；⑤ 重復上述步驟1次，監測并記錄電池的能量和容量等數據。

采用市購同批次的退役18650錳酸鋰電池，使用時間為4 a。選取100節電池進行實驗，電池參數如表1所示，電壓、內阻、容量、能量等電池測試數據如表2所示。

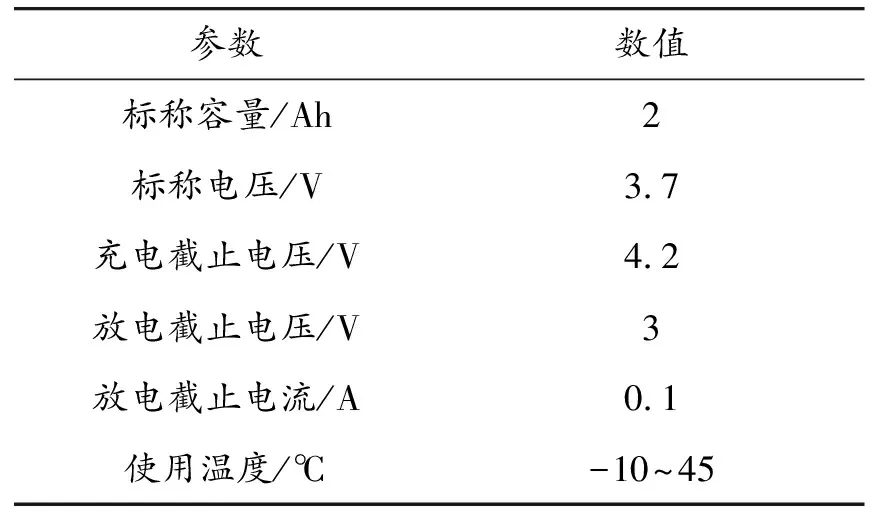
表1 電池參數

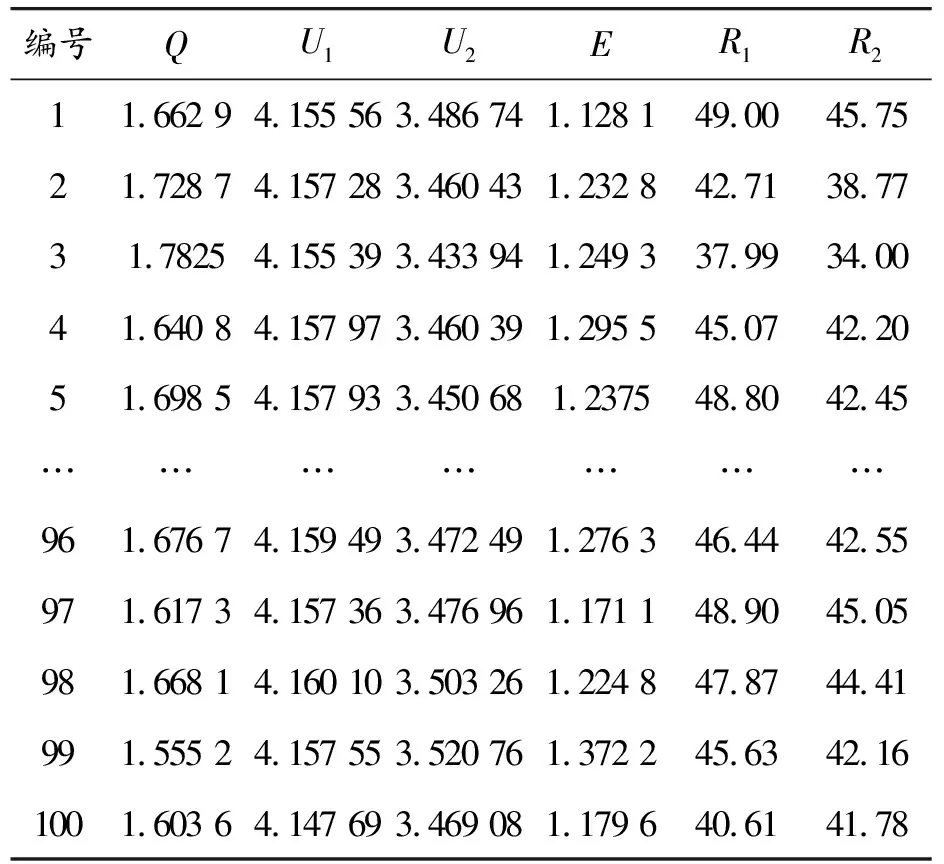
表2 電池測試數據

2 電池分選

2.1 多參數分選

2.1.1分選變量的優化

考慮到各分選變量之間存在相關性，為了減少分選變量，簡化計算，對退役電池的分選變量進行因子分析，式(1)為因子分析模型。

(1)

式中：f1，f2，…，fl(l≤m)為X各分量的公共因子，fi的均值為0，方差為1，相互獨立；εi為xi的特定因子，只對xi起作用。εi均值為0，且各εi相互獨立。f與ε獨立，X均值為0，協方差陣∑=(σij)m×m，矩陣A=(aij)稱為因子載荷矩陣。A中的元素aji稱為xi的方差在fj上的載荷。

對于電池的多分選變量,可以利用KMO檢驗和Bartlett球度檢驗判斷是否適合做因子分析[21]。KMO檢驗通過分選變量之間的相關系數來判斷是否適合做因子分析，KMO值越大，則各分選變量間的相關系數越大，越適合做因子分析。Bartlett球度檢驗通過判斷相關矩陣來檢驗分選變量是否適合做因子分析。Bartlett球度檢驗的原假設為相關矩陣是單位陣，只有拒絕該假設，因子分析才有意義，而要拒絕該假設就需要Bartlett球度統計量相應的概率值Sig小于給定的顯著性水平。

1) 相關系數矩陣求解

記有p個原始電池樣本，x1、x2、…xm為原始分選變量，z1、z2、…zl為新分選變量(主成分)，此時m>l，由于分選參數量綱不同，故對原始數據進行標準化計算(均值為0，方差為1)，然后根據式(2)(3)計算原分選變量間的相關系數矩陣。

(2)

(3)

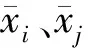
2) 因子載荷矩陣求解

設λ1、λ2、…、λm為相關系數矩陣的特征值，η1、η2、…、ηm為相應的標準正交化特征向量，以特征值大于1為依據確定公因子數。求出公因子對應的標準正交化特征向量，則樣本相關系數矩陣主成分分析的因子載荷矩陣為：

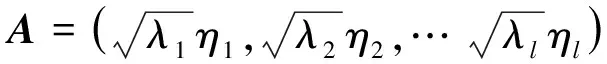
(4)

ηj為在跡的意義下fj對X的方差貢獻：

(5)

gj為A的第j列各元素的平方和：

(6)

對因子載荷矩陣做正交旋轉，使得到的矩陣C1=CD方差最大，其中D為正交矩陣。

3) 計算因子變量得分

采用回歸法求各個原始數據在不同公因子上的詳細數據值，即因子變量得分。以100節電池6個分選變量的數據作為輸入，得到相關矩陣元素,如表3所示，6個變量有較大的相關性。

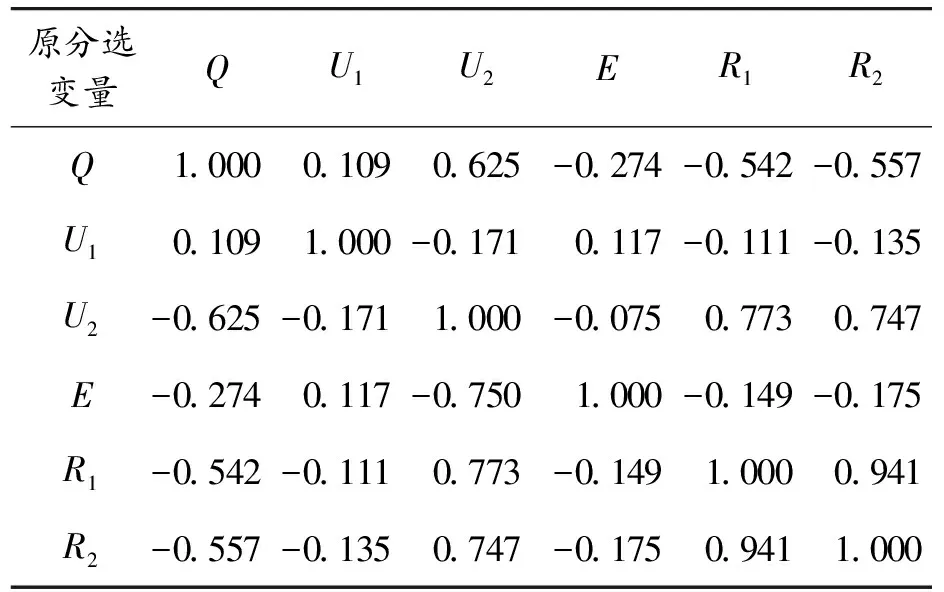
表3 分選變量的相關矩陣元素

根據KMO度量標準，檢驗值大于0.7時，適合做因子分析[21]。如表4所示，其檢測值KMO=0.711>0.700，表明樣本數據適合進行因子分析。此外，Bartlett球度統計量相應的概率值Sig=0.000<0.050，小于給定的顯著性水平，拒絕原假設，可以進行因子分析[22]。通過KMO和Bartlett檢驗，表明各分選變量滿足因子分析條件。

表4 Bartlett和KMO檢驗結果

采用主成份分析法進行因子分析，表5為主成份貢獻率，其中F1、F2的特征值大于1，故選取F1、F2這2個公因子作為代表原分選變量的新變量。

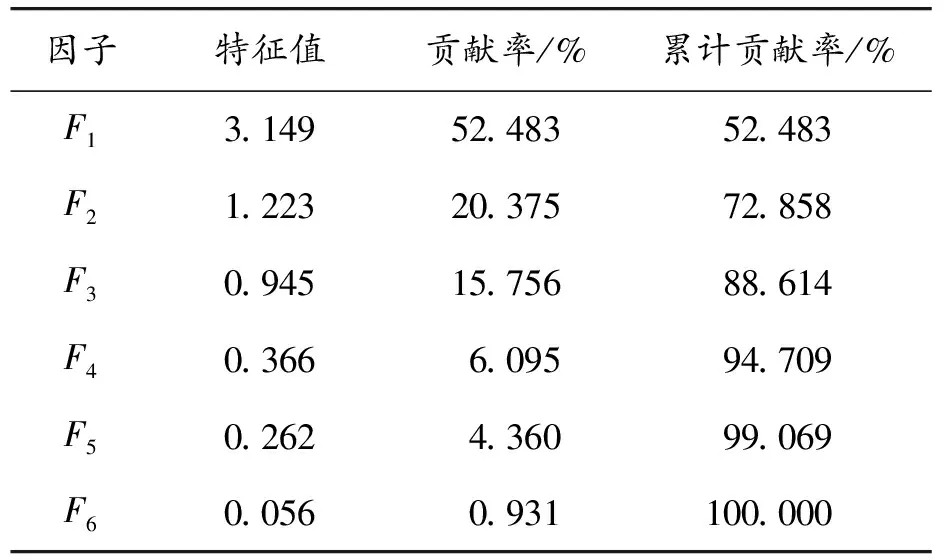
表5 主成分貢獻率

表6中每列數據表示公因子被原始變量表示的系數。

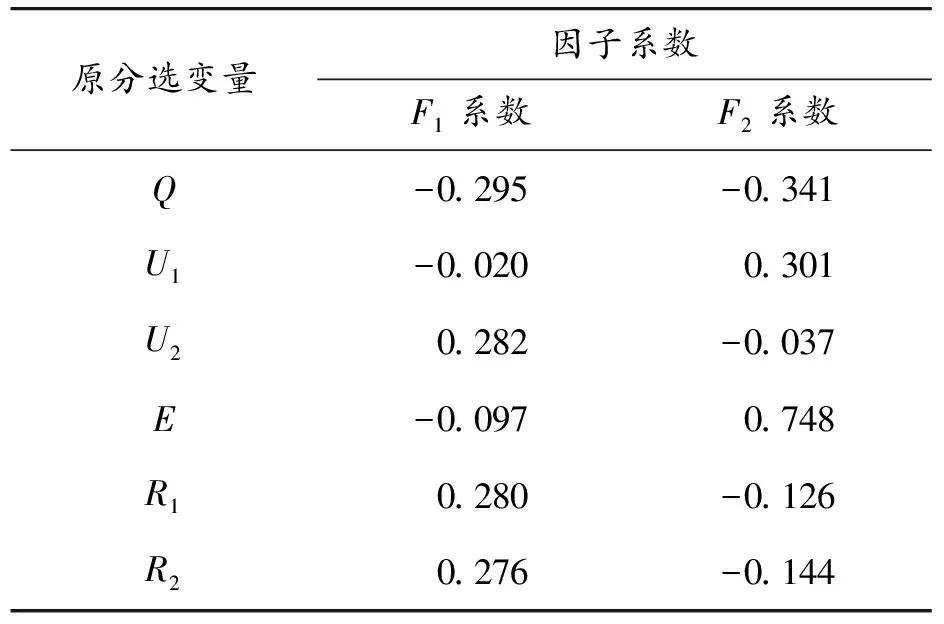
表6 成分得分系數矩陣

因子分析后6個參數轉換成2個參數就可表達原來分選變量的大部分信息，所以選取這2個公因子作為新的分選變量。

F1=-0.295Q-0.020U1+0.282U2-

0.097E+0.280R1+0.276R2

F2=-0.341Q+0.301U1-0.037U2+

0.748E-0.126R1-0.144R2

2.1.2多參數分選結果

運用組間連接聚類方法，以平方歐式距離為度量標準對電池進行分類。

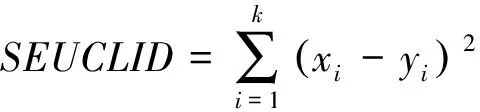
(7)

式中：xi和yi分別代表2個退役電池樣本的某個變量，i和k代表變量個數。

分選結果如表7所示，采用式(8)(9)計算分選后各類電池電壓的離散情況。

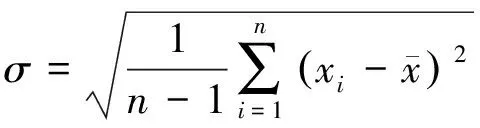
(8)

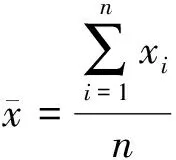
(9)

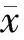
分選前100節退役鋰離子電池的電壓標準差為0.043 1，分選后第Ⅰ類電池的電壓標準差為0.203 7，第Ⅱ類電池的電壓標準差為0.011 1。可以看出，第Ⅰ類電池的電壓一致性較差，表明電池組性能衰減是由極少數電池性能衰減引起的。

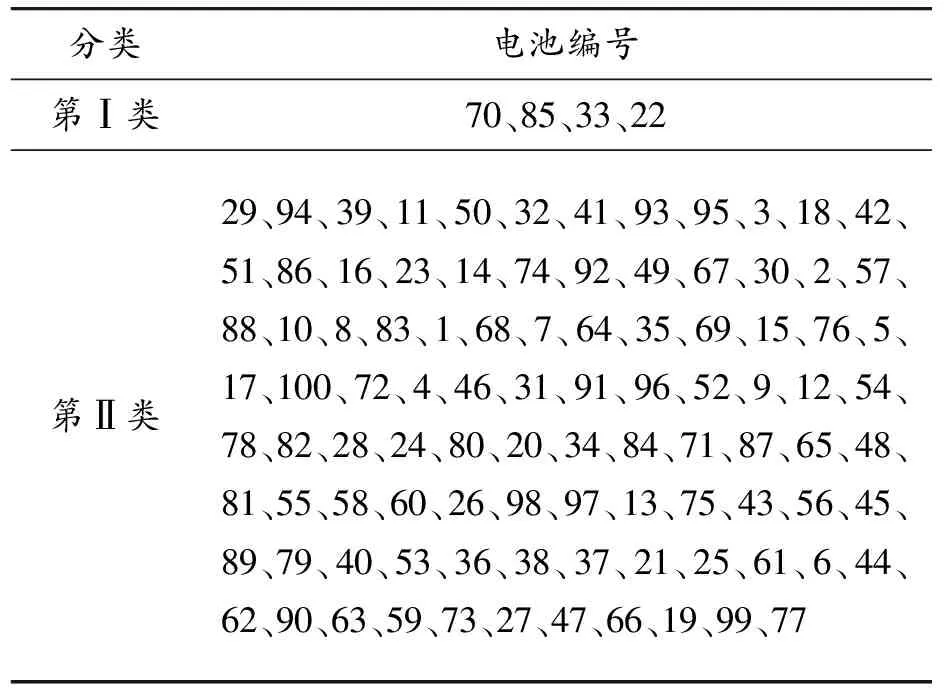
表7 多參數分選結果

2.2 動態分選

多參數分選只能體現電池的靜態一致性，無法反映充放電過程中電池動態特性。動態特性分選法考慮了電池在充放電過程中的參數動態變化，結合多參數分選能夠獲得更高的一致性。多參數分選結果顯示第Ⅰ類電池一致性相對較差，因此在第Ⅱ類(96節)電池的基礎上再進行動態分選。

現有的動態分選方法普遍使用電壓曲線進行分選，但該方法不能反映電流、容量等性能參數。任意一節電池充放電曲線如圖2。恒壓充電時電壓曲線不能表示電池能量和容量的變化趨勢；擱置時的能量曲線不能表示電池電壓變化情況。電池組合時需同時考慮電壓和容量的一致性以避免能量浪費，故同時使用電壓曲線和能量曲線對第Ⅱ類96節電池進行動態分選，其數據如圖3、4所示。

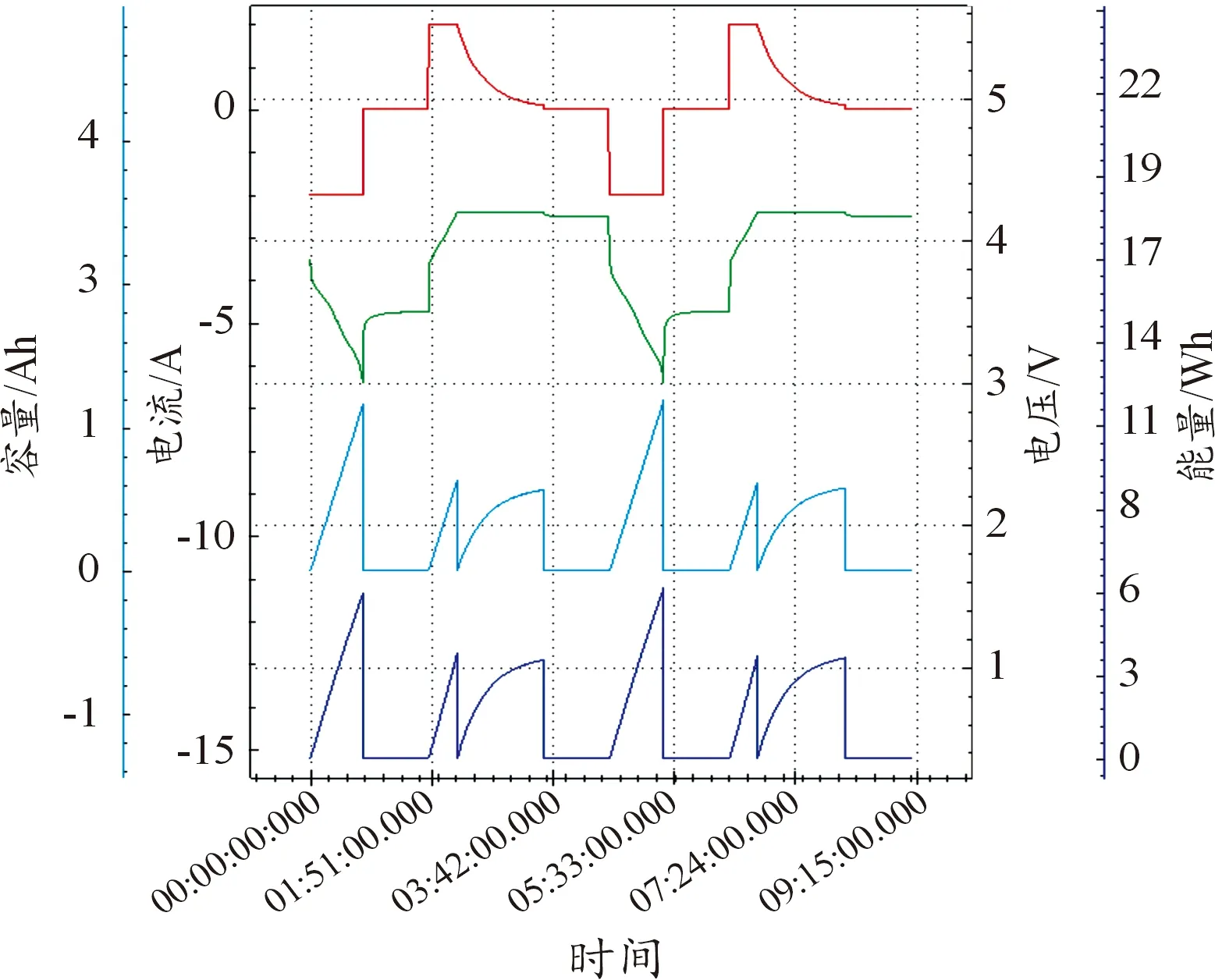
圖2 電池充放電曲線

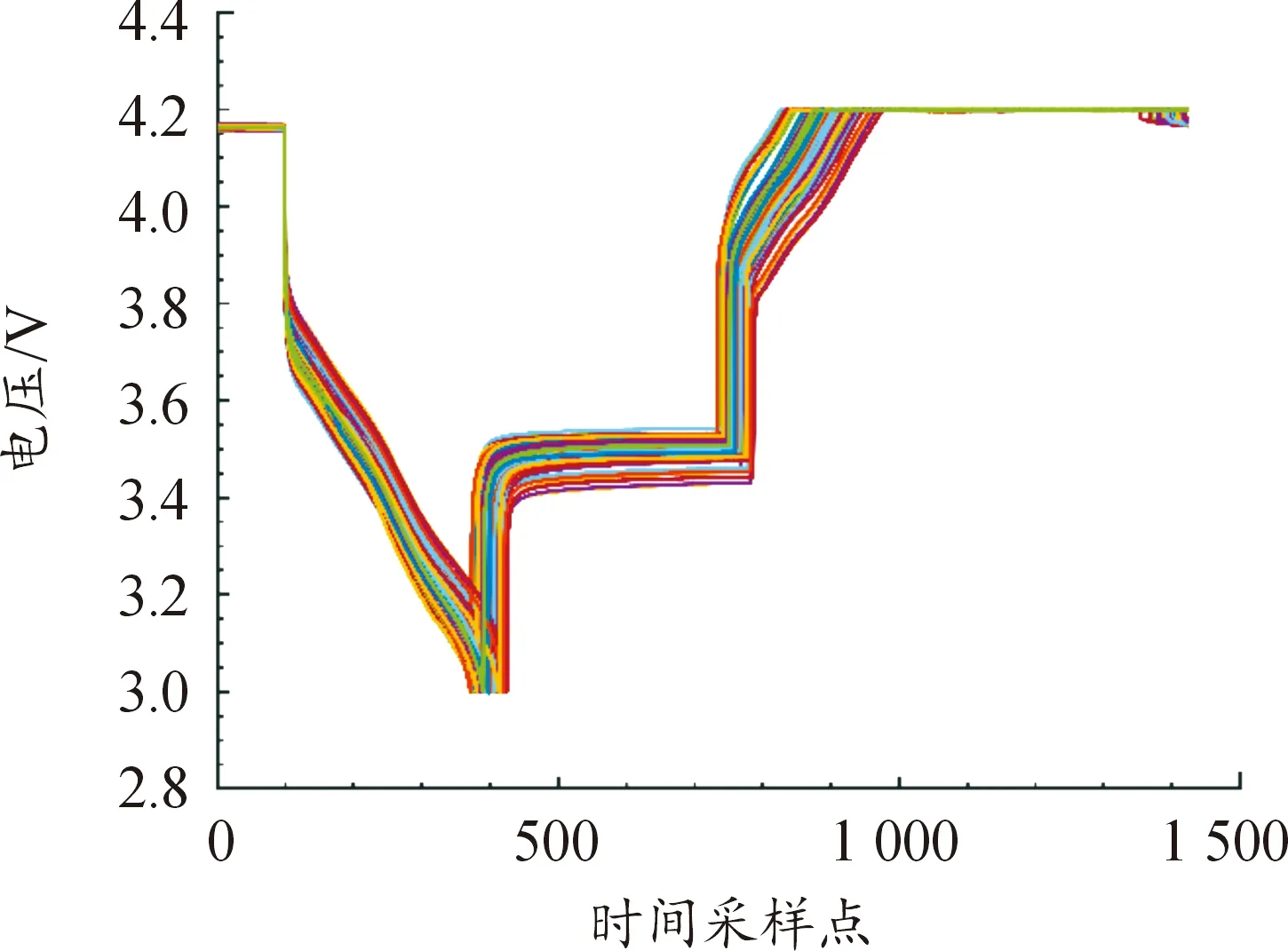
圖3 電壓曲線

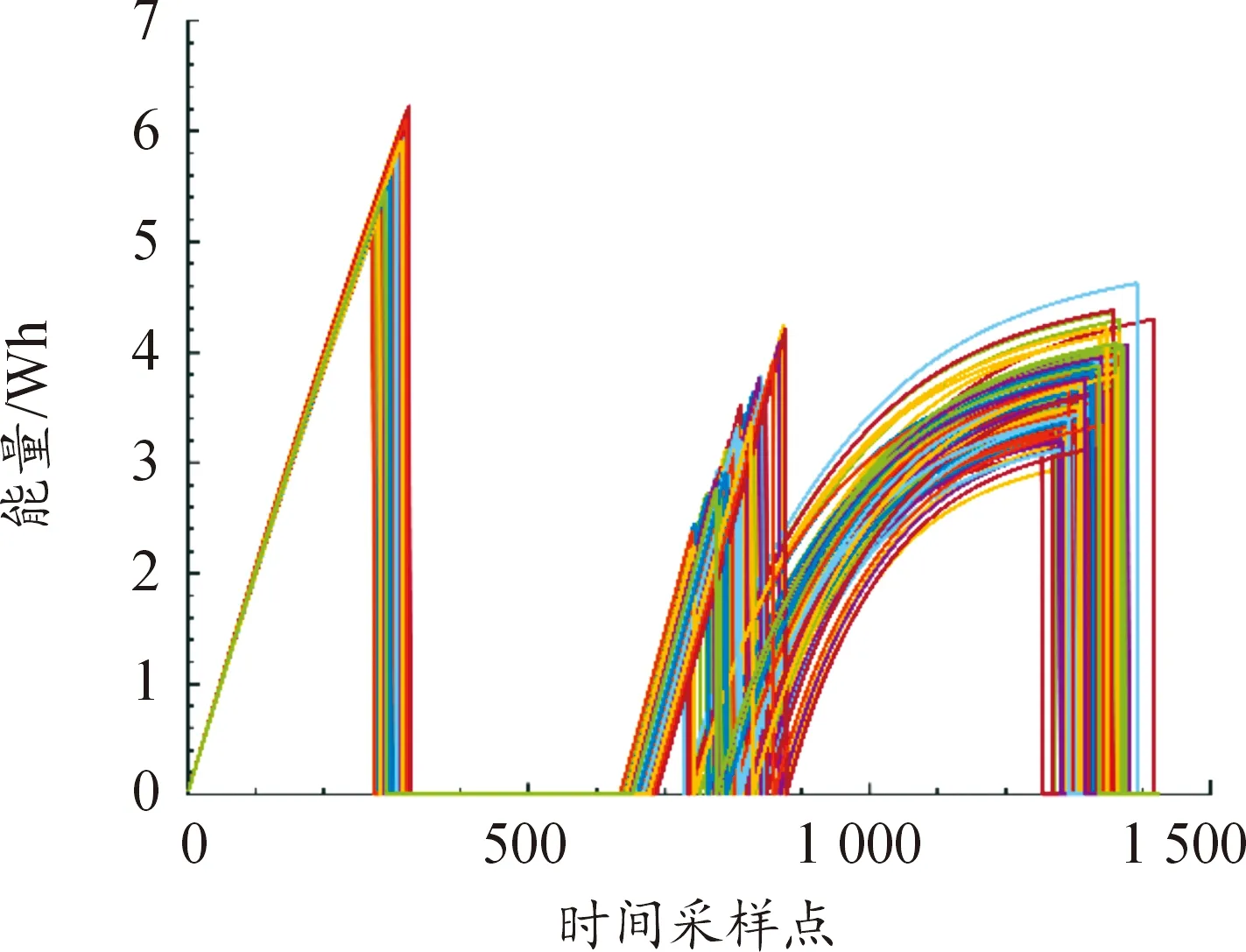
圖4 能量曲線

算法設計：

步驟1采集96個電池電壓和能量曲線上的數據并根據式(10)(11)分別歸一化至[0,1]區間：

(10)

(11)

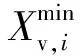
步驟2針對K-means算法存在K值不確定的問題，根據式(12)計算步驟1所得電壓曲線和能量的距離均值，得到頻率分布直方圖和頻率分布曲線，并根據直方圖和分布曲線分析確定K值：

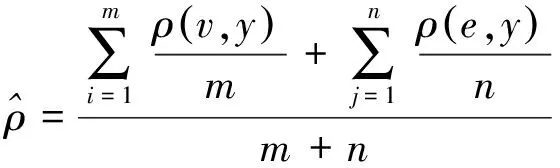
(12)

式中：m代表電壓曲線上點的個數；n代表能量曲線上點的個數；ρ(v,y)代表電壓曲線上點的縱坐標值；ρ(e,y)代表能量曲線上點的縱坐標值。

步驟3由步驟2確定K-means算法的K值，隨機選取K個聚類中心曲線，并設置最大迭代次數；

步驟4根據式(13)計算剩余曲線到聚類中心曲線的平均距離，并將它們歸類到距離3條聚類中心曲線平均距離最近的一類中；

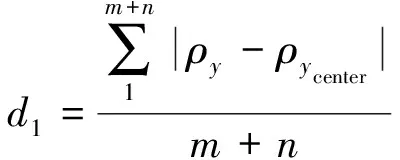
(13)

式中：ρy代表電壓和能量曲線上點的縱坐標值；ρycenter代表聚類中心曲線上點的縱坐標值。

步驟5迭代步驟3—4并根據式(14)計算平均歐式偏差至所有曲線的平均歐式偏差最小，算法結束。

(14)

式中：p代表所有退役鋰離子電池個數。

步驟6輸出頻率分布直方圖和頻率分布曲線、平均歐式偏差和聚類結果。

頻率分布直方圖與頻率分布曲線如圖5所示，數據近似圍繞3個峰值緊密聚集，故可以設置3個聚類中心進行處理。經分析可知，第Ⅱ類96個電池可分為3類。

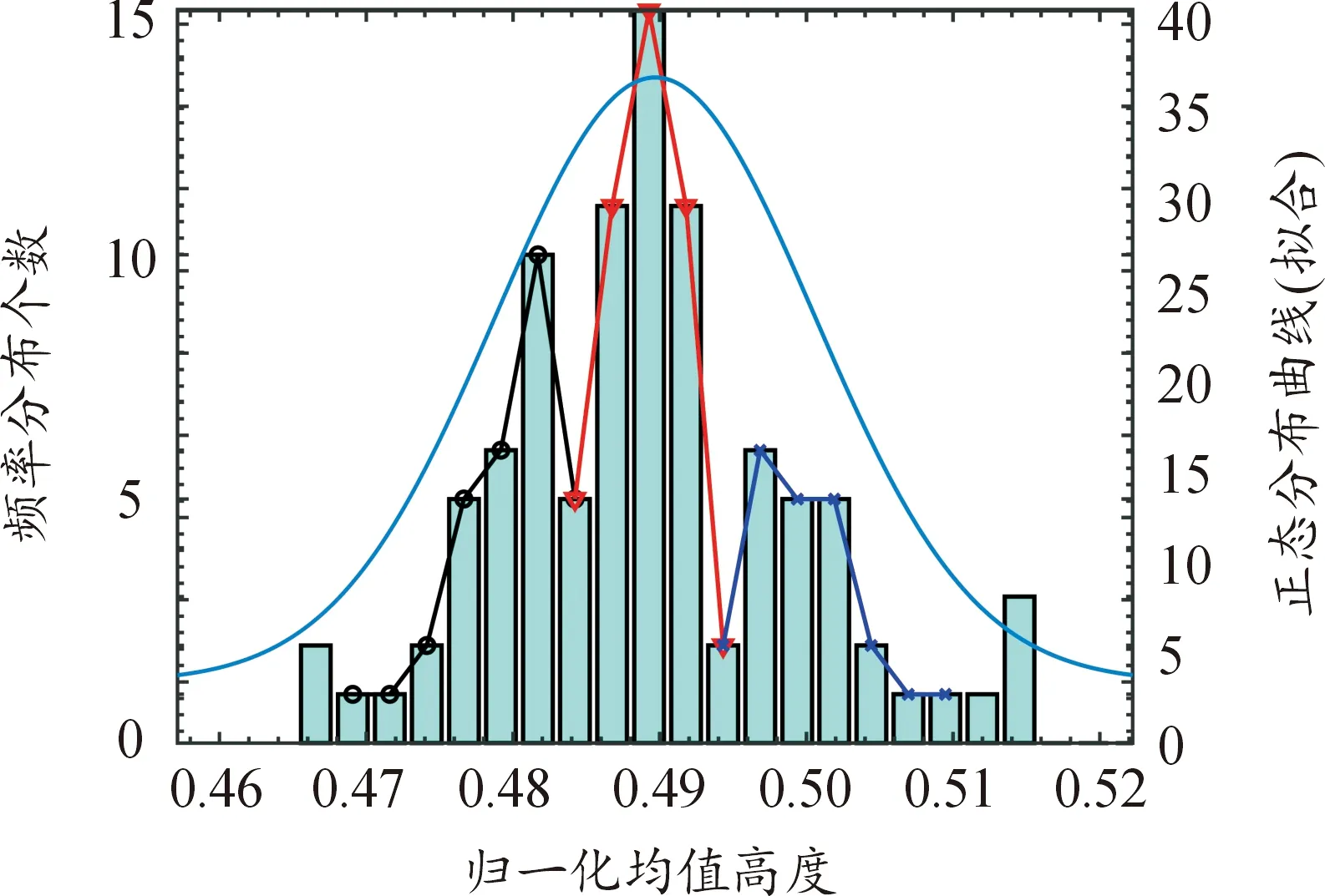
圖5 頻率分布直方圖與頻率分布曲線

圖6顯示了迭代100次后使得平均歐式偏差值最小時的3條聚類中心曲線。

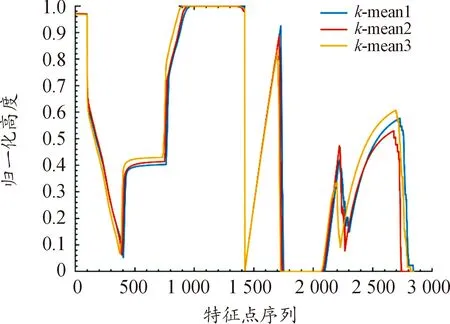
圖6 聚類中心曲線

平均歐式偏差可以反映迭代過程中所有曲線平均歐式偏差的變化。如圖7所示，經過4次迭代后，平均歐式偏差趨于定值0.068 8，表明迭代后聚類趨于平穩，證明了算法聚類結果的優越性和穩定性。

圖7 平均歐式偏差曲線

最終獲得電池的分選結果如表8所示。

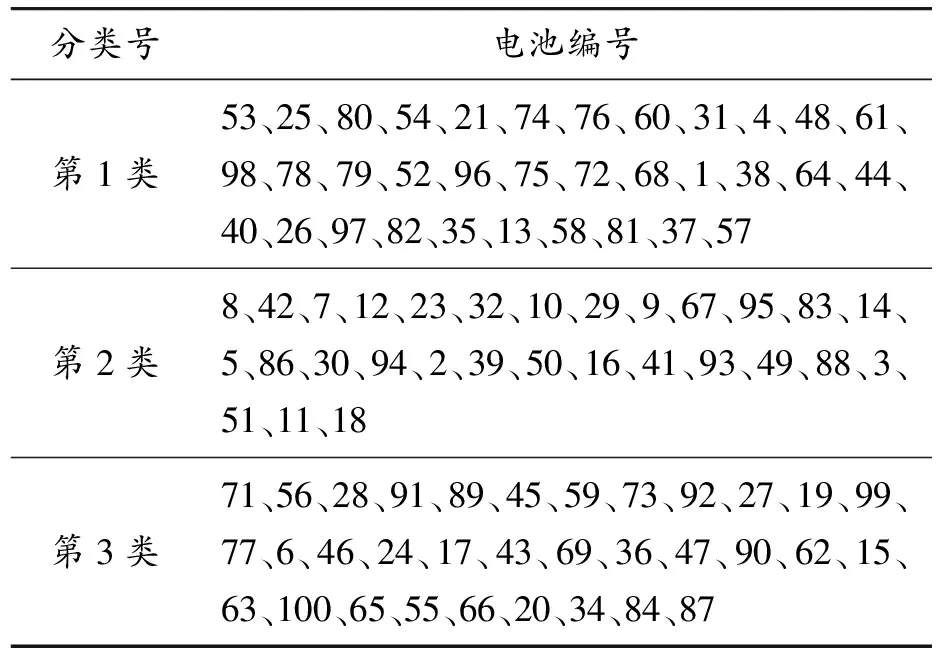
表8 電池最終分選結果

為了評價動態分選的效果，采用式(8)(9)計算各類電池充電電壓、放電電壓、容量的離散情況。

分選結果如表9所示。同時采用電壓和能量曲線分選后(第1、2、3類)的電池充電電壓一致性分別提高了約94%、82%、60%，放電電壓一致性分別提高了約23%、41%、10%，容量一致性分別提高了約67%、54%、54%。

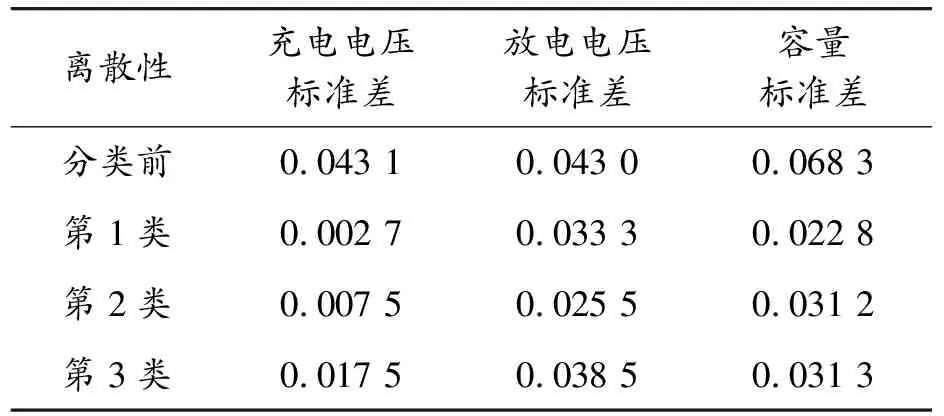
表9 分選結果

如圖8所示，為了使分選結果更加直觀，使用雷達圖對分選結果進行分析。雷達圖中離原點越近代表一致性越好。

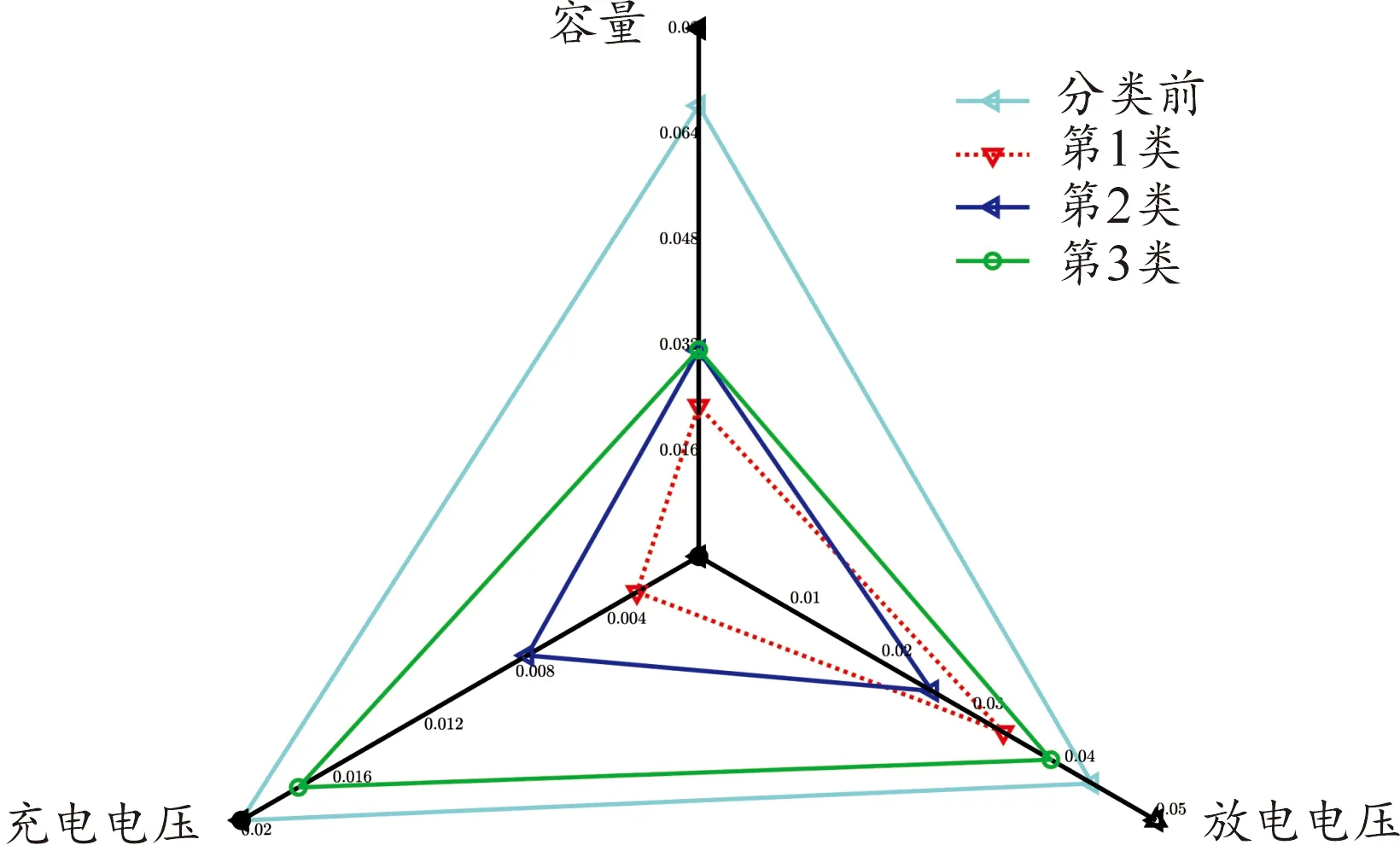
圖8 分選結果

3 結論

1) 第Ⅰ類電池的一致性較差，表明電池組性能衰減是由極少數電池性能衰減引起的。

2) 同時考慮電壓和能量曲線分選后的退役鋰離子電池充電電壓一致性最大提高約94%，放電電壓一致性最大提高約41%，容量一致性最大提高約67%。表明該分選策略得到的分選結果更好，對電池組性能提升有很大幫助。

3) 提出的通過頻率分布直方圖和頻率分布曲線分析確定K-means算法K值的方法具有參考價值。

4) 分選前電池容量和電壓存在較大的差異，從不同類別看，電壓一致性和容量一致性并不是正相關，且不同應用場景對于各參數要求并不相同，表明同時考慮電壓和能量曲線分選的必要性。接下來將對不同應用場景下電壓和能量曲線的權重展開研究。