CKDO 一方程模型計算高超聲速橫流轉捩

王 浩，徐晶磊

(1.北京航空航天大學 能源與動力工程學院，北京 100191；2.上海交通大學 航空航天學院，上海 200240；3.北京航空航天大學杭州創新研究院（余杭）航空學院，杭州 310023)

0 引言

高超聲速轉捩對高超聲速飛行器的飛行狀態有顯著影響，主要體現在氣動熱/力與動力方面。一方面，轉捩后湍流的壁面摩擦力和傳熱速率遠高于層流，大約是3～5 倍[1]，使得高超聲速飛行器熱防護系統的設計非常具有挑戰性；轉捩后的氣動載荷分布也會發生顯著變化，影響氣動配平、帶來飛行安全問題。另一方面，湍流邊界層的抗分離能力更強，可以有效地克服超燃沖壓發動機入口處的邊界層分離，并且湍流邊界層的摻混能力也更強，可以增強發動機中燃料與空氣的摻混，使燃料可以充分燃燒。如果能夠準確預測到轉捩的位置和區域，就更有把握通過優化外形、改變壁面條件等多種手段來延遲或促進轉捩的發生，以滿足種種工程需求。在真實飛行器的三維邊界層中，受壓力梯度和后掠角的共同作用，邊界層內近壁區往往會出現與邊界層外勢流平面內流線方向垂直的流動分量，稱為橫流流動[2]。當橫流速度出現拐點時，將會產生流動失穩并容易發展為三維邊界層轉捩。因此，高超聲橫流轉捩的研究有著迫切的實際需求，發展相應的預測或計算方法具有重要的工程意義。

高超聲速橫流轉捩是集來流湍流-激波相互作用、可壓縮湍流、橫流、轉捩等復雜流動因素于一身的、長期困擾科研人員的難題。轉捩本身的難點在于，其起始位置對擾動的演化十分敏感，只有精確計算出擾動的演化過程才能得到準確的起始位置。而演化過程涉及到上述4 個問題的前3 個，即使這3 個問題得到準確建模，建模公式的同時使用也可能產生耦合誤差。目前在工程應用層面，基于雷諾平均N-S方程（RANS）的湍流/轉捩模型是預測轉捩較為實際和有效的選擇。2000 年Suzen 和Huang[3]構造出間歇因子輸運方程，它與湍流輸運方程合并成為轉捩模型。2006 年Menter 等[4-5]構造出γ-Reθ-SST 四方程轉捩模型，只采用當地流動變量，從而與現代CFD 程序兼容。隨后該模型集成在ANSYS 商業軟件，達到工業級成熟度，成為轉捩模型的標桿。該模型沒有考慮轉捩機理，而是基于經驗關系式構造轉捩判據，而經驗關系式是通過低速湍流邊界層、壓氣機等標定的。2009 年王亮和符松[6]提出k-ω-γ轉捩模型，對超聲速平板邊界層和超/高超聲速圓錐邊界層的預測結果與試驗結果定量符合。直到2016 年，周玲在高超聲速轉捩模型中引入了橫流模態時間尺度和橫流轉捩準則，對原模型預測的HIFiRE-5 橫流轉捩圖像有所改善，是高超聲速橫流轉捩的先驅建模工作。2016 年張毅鋒等[7]對γ-Reθ-SST 轉捩模型的低速經驗關系式進行間歇因子的馬赫數修正和湍流普朗特數修正，顯著改進了原模型的性能，對多個高超聲速尖錐的計算結果與試驗符合較好。2017 年張毅鋒等[8]進一步引入以橫流雷諾數為基礎的轉捩準則，對HIFiRE-5 橫流轉捩標模，在不同雷諾數下都取得了與噪聲風洞實驗非常吻合的計算結果。2021 年向星皓等[9]使用eN方法對高超聲速橫流轉捩數據進行拓展，結合橫流強度與表面粗糙度構造當地化的高超聲速橫流轉捩判據，構造的新模型對多狀態下的高超聲速尖錐進行橫流轉捩預測，取得了與實驗結果符合較好的預測效果。

從上述間歇因子轉捩模型的進化路線來看，為了捕捉高超聲速橫流轉捩，在保證常規轉捩的預測精度的同時，還需引入高超聲速（或可壓縮）效應和橫流判據等，建模難度和工作量很大。基于RANS 的“轉捩模型”還有一條古老的路線，那就是直接用湍流方程（k、ω等）計算轉捩。2019 年徐晶磊等將KDO 模型[10-11]推廣至轉捩的計算[12-13]，具體做法是，以輸運變量r=μt/μ重新標定模型參數，使模型整體達到流動結構自適應。而模型捕捉轉捩的機制是，通過流動結構的自適應和湍流輸運特性的保存，自發演化出轉捩。這樣，不用引入特定的轉捩機理，卻有可能捕捉到特定類型的轉捩，具有潛在的多機理普適性。目前，該模型已成功預測了T3A 與T3B 平板邊界層旁路轉捩、T3A-平板邊界層自然轉捩、Aero-A 翼型分離泡轉捩、DLR-F5 橫流轉捩、6 ∶ 1 橢球橫流轉捩、超聲速平板邊界層轉捩以及超聲速尖錐轉捩。本文將該模型推廣至高超聲速橫流轉捩的預測，采用經典標模HIFiRE-5，評估其捕捉高超聲速橫流轉捩的潛力與不足，為高超聲速橫流轉捩模型的發展提供參考。

1 CKDO 轉捩模型

1.1 CKDO 湍流模型

精確的可壓縮湍動能控制方程[14]為：

對于可壓縮湍流，可壓縮效應的建模是十分必要的。對于可壓縮修正的KDO 模型，即CKDO 模型，方程右端各項依次分別模化為：

為了維持計算的穩定性，ε2的建模被分為兩層建模，分別黏性子層和外層:

若Rek＜10，

若Rek＞10，

模型中的許多經驗數值，只是為了精準刻畫從DNS 數據得到的r～Rb與Rek～Aε分布曲線而采用的多層結構標定方法，導致的多層系數[12]。本質上，模型的經驗參數只有2 個，即雷諾應力本構關系的Bradshaw 參數Rb及ε方程毀滅項系數Aε，這兩個經驗參數經平板邊界層的Reθ=4 060 剖面標定后，就再未改變。

1.2 CKDO 轉捩模型

注意到，雷諾應力本構關系中的Bradshaw 系數，在公式（9）被標定為關于Rek的函數，Rek包含壁面距離，而無論流動形態如何，壁面距離是固定不變的，不反映流動結構，這就是為什么原始 KDO 在T3B 平板算例中展現轉捩行為，但轉捩過早。KDO 以及CKDO 轉捩模型引入湍流黏性與層流黏性之比r，它傳達湍流的強度，是一個輸運變量。再次使用平板邊界層的Reθ=4 060 截面把Rb標定為：

CKDO 和KDO 模型的經驗參數標定于充分發展平板湍流邊界層的Reθ=4 060 剖面，但又能用于充分轉捩區域甚至橫流區域，這一點是令人疑惑的。解釋如下：首先，理論上允許這樣的CFD 計算系統存在，正如N-S 方程一樣，并不考慮任何的轉捩機理，卻能捕捉轉捩，CKDO-tran 計算轉捩的機制與N-S 方程是一致的。其次，可以注意到，CKDO 和KDO 捕捉轉捩的關鍵在黏性比r=μt/μ＜ 1 的涵蓋層流區域和層流-湍流轉捩區域（“pre-transition”區域）。只要r＜1 時，模型采用的相似性規律是普適的，那么模型就能普適預測轉捩。實際情況是，當r＜ 1 時，公式（14）在Reθ=150～900 的“pre-transition”區域仍然普適成立[12]。為什么普適?r＜ 1 的區域常常對應于y+＜20 的非常近壁區，即黏性子層和部分過渡層，而該區域的流動屬于壁面主導的流動，該區域的流體微團只感受到壁面的影響而基本無視外界的影響，形成一個普適的“局部平板邊界層”。將采用公式（14）的CKDO 模型記作CKDO-tran，將采用公式（14）的KDO 模型記作KDO-tran。

2 超聲速轉捩算例評估

為了展示對于超聲速轉捩流動，考慮可壓縮效應的CKDO-tran 模型相對于KDO-tran 模型的優勢，本節使用超聲速平板邊界層的DNS 數據作為基準驗證算例。德州大學的Jiang 等[15]進行了來流馬赫4.5 的平板直接數值模擬（U∞=705.093 m/s，T∞=61.111 K），壁溫恒定等于層流流態下的絕熱溫度。文獻用oblique-mode 擾動激發湍流，這意味著來流的湍流度未知，因此不同的研究者采用不同的來流湍流度，來使他們的模型獲得最佳表現。對于KDO-tran 和CKDO-tran，來流湍流度分別取1%和0.73%，計算結果見圖1。CKDO-tran 預測的湍流區摩阻大小與DNS 結果更接近，且捕捉到了轉捩后的摩阻波動；而KDO-tran 預測的摩阻偏低且過于平滑，原因在于未考慮可壓縮效應。低估超聲速流動的摩阻，這一現象在文獻[16]也有體現，就是因為各轉捩模型搭載的湍流方程忽略了可壓縮效應的緣故。然而KDOtran 計算的轉捩過渡段好于CKDO-tran，這與KDOtran 的一貫表現不一致（KDO-tran 的轉捩過渡段總是很短），推測是KDO-tran 的湍流黏性過小，對過渡段造成了緩沖，歪打正著。

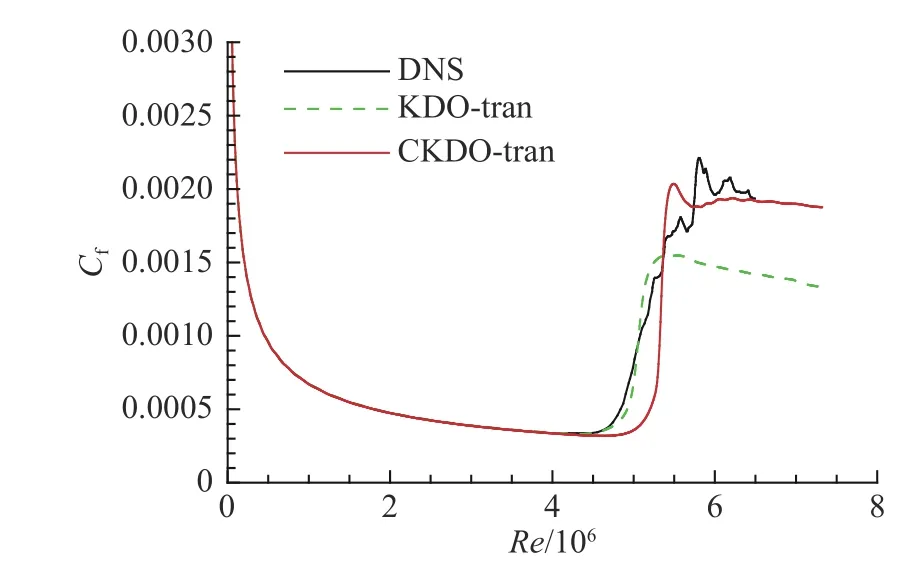
圖1 平板表面摩阻分布Fig.1 Skin friction distribution on the flat plate

3 高超聲速橫流轉捩算例評估

HIFiRE（Hypersonic International Flight Research Experimentation）是由美國空軍研究實驗室和澳大利亞防衛科研組織聯合舉辦的高超聲速飛行器測試項目，其目的是發展和驗證下一代高超聲速系統的關鍵技術。其中HIFiRE-5 外形設計為長短軸之比為2 ∶ 1 的橢圓錐，使得三維效應和橫向流動更加明顯，被專門用于研究高超聲速三維邊界層轉捩。本文計算采用Juliano 等[17-20]風洞試驗中的HIFiRE-5 縮比模型，總長為328 mm，橫截面長軸半徑為82 mm，短軸半錐角為7°，短軸所在截面頭部半徑為0.95 mm，模型三維示意圖如圖2 所示。HIFiRE-5 模型的計算網格采用從短軸中心線平面劃分的二分之一模型，計算采用三重網格并行計算技術，共分8 個網格塊，每個網格塊的各邊網格點數均控制為4n+1，經過網格無關性驗證后，最終模型計算網格流向共181 個網格點，法向共113 個網格點，周向共129 個網格點，總網格量約為252 萬。法向第一層網格高度約為5×10-4mm，并在激波位置附近加密。HIFiRE-5 結構網格三維示意圖如圖3 所示。

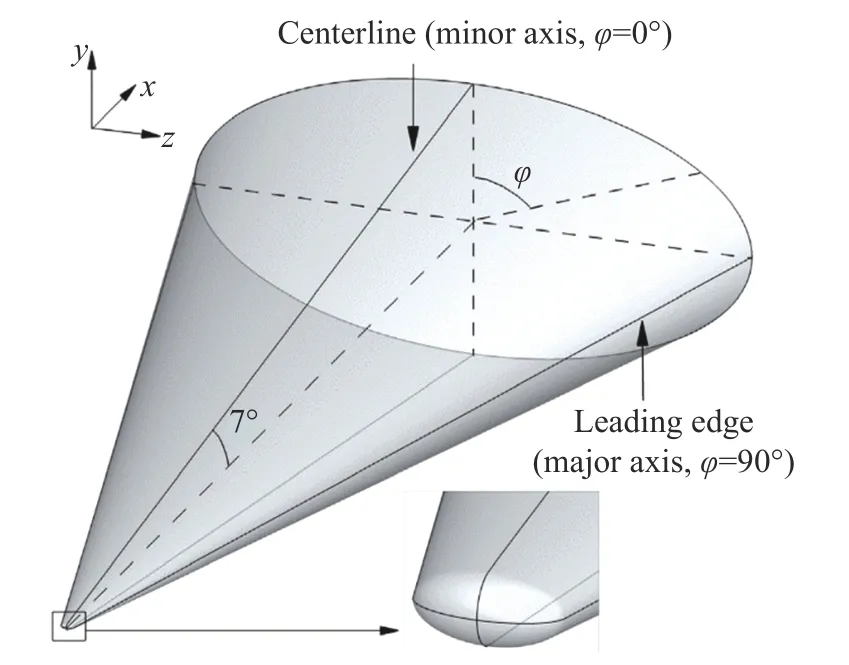
圖2 HIFiRE-5 模型三維示意圖Fig.2 3D model of HIFiRE-5

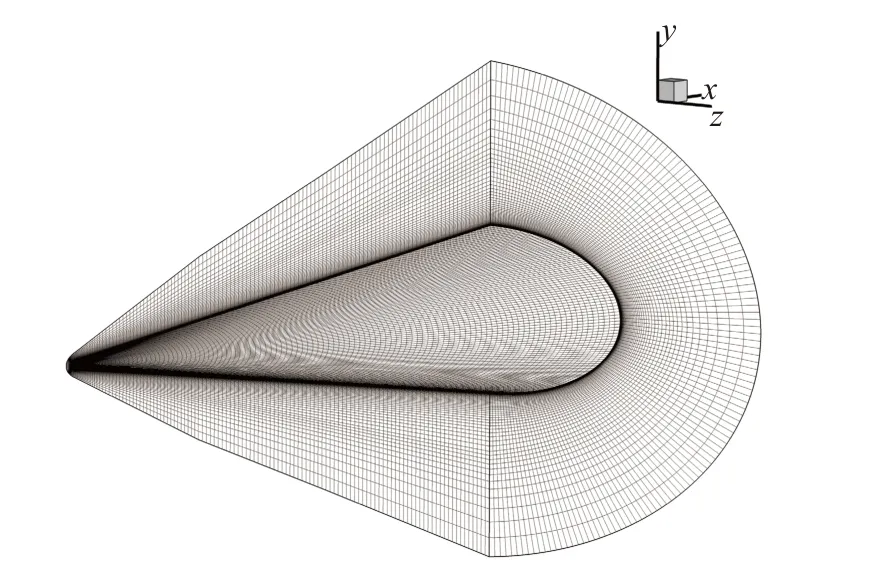
圖3 HIFiRE-5 結構網格示意圖Fig.3 Structured mesh of HIFiRE-5

本節主要模擬HIFiRE-5 模型在不同雷諾數、湍流度和迎角的工況下的轉捩結果，并與Juliano[17-20]等的風洞實驗結果進行對比分析。實驗來流馬赫數Ma=5.8，來流總溫T0=410 K，等溫壁面溫度Twall=300 K。變化的單位雷諾數Re、迎角條件α、以及來流湍流度Tu，其工況在表1 中給出。

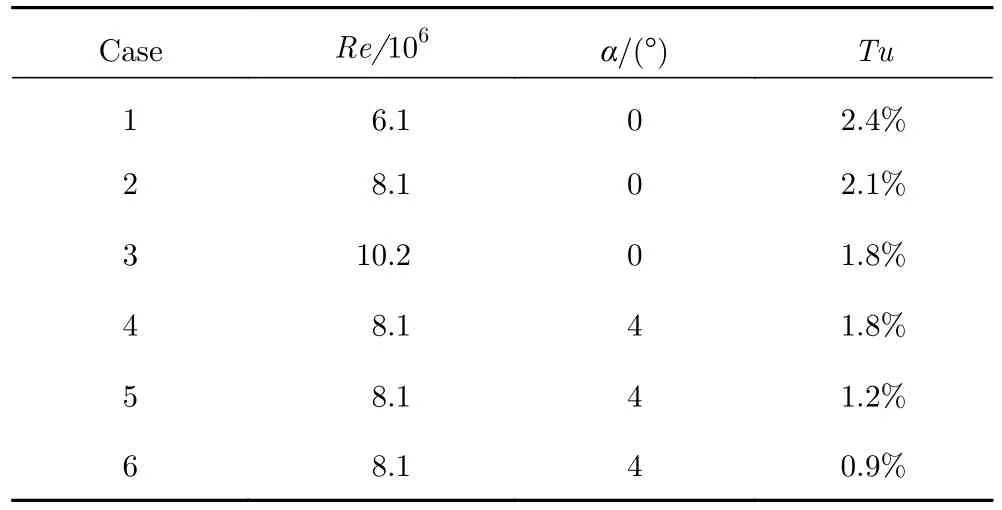
表1 HIFiRE-5 模型實驗工況Table 1 Experimental setup of HIFiRE-5

邊界層發生轉捩，最顯著的特征以及影響是壁面摩擦阻力和熱流系數的急劇上升，這也是目前判斷邊界層轉捩與否的常見方法之一。Juliano 等使用溫敏漆（temperature-sensitive paint，TSP）技術進行測量分析，溫敏漆顯示的強度與溫度變化成正比，所以可以用來判斷壁面熱流系數的相對大小，如果觀察到熱流急劇升高，即為發生邊界層轉捩現象。圖4（a）顯示了HIFiRE-5 模型在單位雷諾為10.2 × 106/m 工況的壁面溫度變化ΔT分布，對應計算算例Case3。Case3正是各文獻研究較多的工況，本文亦圍繞這一工況開展多種效應研究。

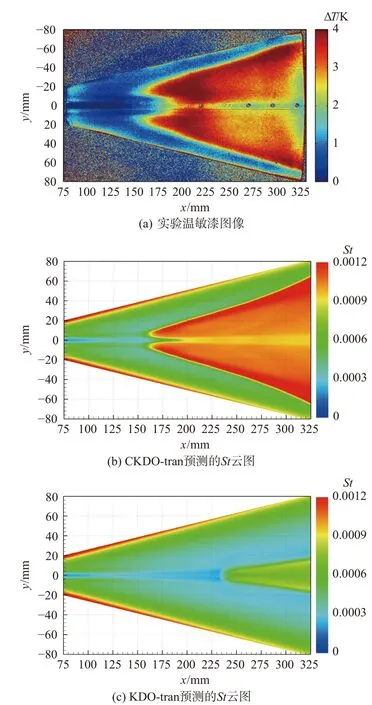
圖4 Case3 轉捩圖像Fig.4 Transition pattern of Case3

3.1 可壓縮效應

高超聲速狀態下，湍流的可壓縮效應十分顯著，需要對湍流模型進行可壓縮修正。本節主要評估可壓和不可壓兩個版本的KDO 轉捩模型，即CKDO-tran和KDO-tran 的預測能力。圖4（b）和圖4（c）顯示分別的是CKDO-tran 和KDO-tran 預測的Stanton（St）分布，可通過St計算出實際熱流。可見，CKDO-tran 預測的雙肺葉轉捩圖像與實驗符合較好，而在此湍流度下KDO-tran 也預測出雙肺葉轉捩圖像，但轉捩位置顯著推遲了，造成轉捩形狀、大小與實驗差距很大。此外，對KDO-tran 還進行了變來流湍流度計算，無論怎么調整來流湍流度，都無法取得與實驗符合的轉捩圖像。CKDO-tran 和KDO-tran 的計算結果表明，對于用湍流模型直接計算轉捩的方法，可壓縮效應的引入對高超聲速橫流轉捩的預測至關重要。

3.2 多雷諾數工況評估

Juliano 的風洞實驗在保證多數來流參數的條件下，進行了多個變雷諾數工況研究。文獻多是對Case3 的雷諾數工況進行研究，本文將轉捩模型拓展至更多雷諾數的研究，一方面通過更多工況驗證模型的適用性、另一方面為他人的對照研究提供參考。圖5、圖6 給出Case1、Case2 工況下，實驗溫敏漆顯示的轉捩圖像和CKDO-tran 計算的St云圖。聯合Case1、Case2、Case3 的實驗轉捩圖像來看，隨著雷諾數的增加，轉捩形成的高溫雙肺葉區域面積增加，并且形狀變得更加瘦長。CKDO-tran 的計算結果符合這種趨勢，且預測的轉捩圖像與實驗總體符合較好。

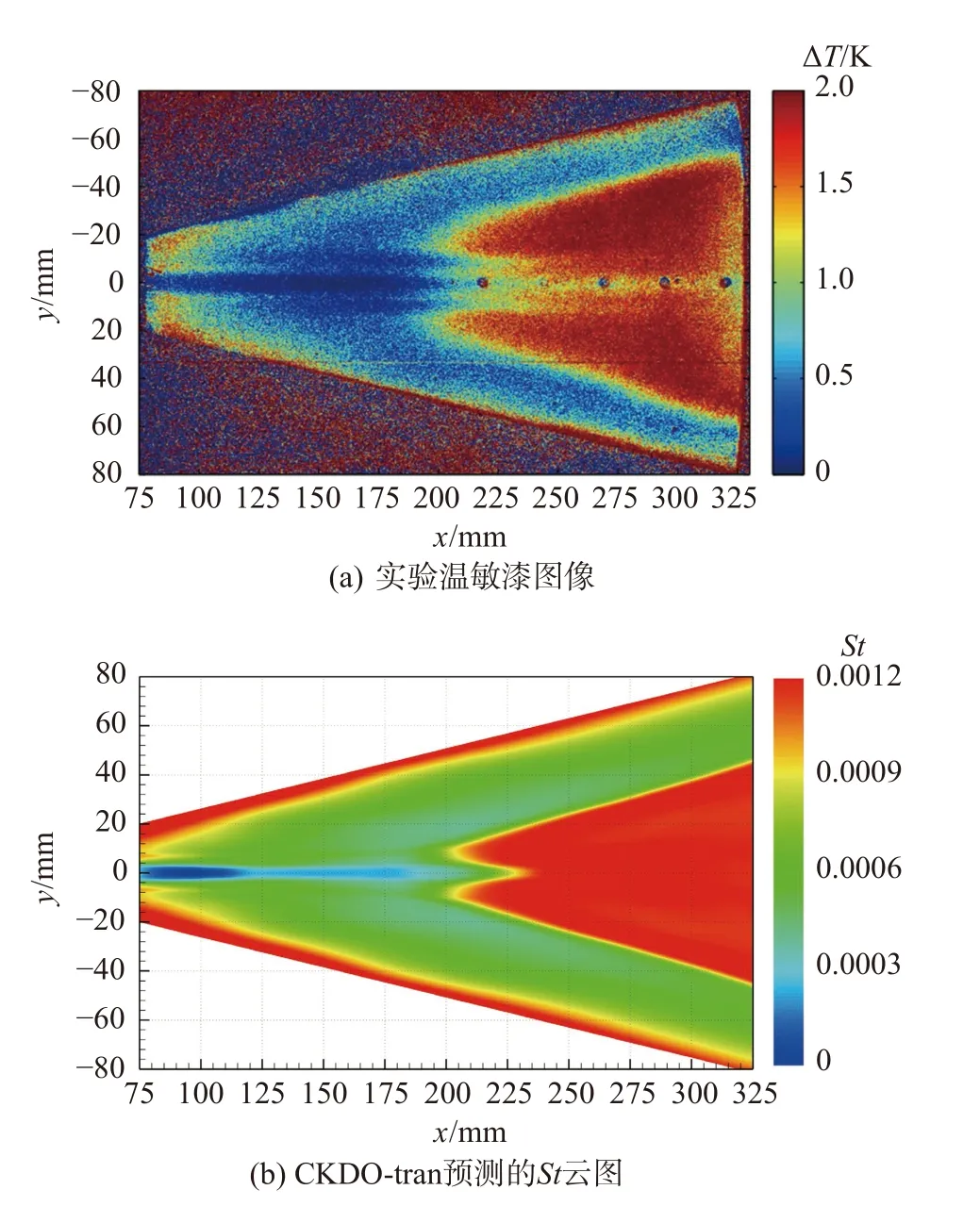
圖5 Case1 轉捩圖像Fig.5 Transition pattern of Case1

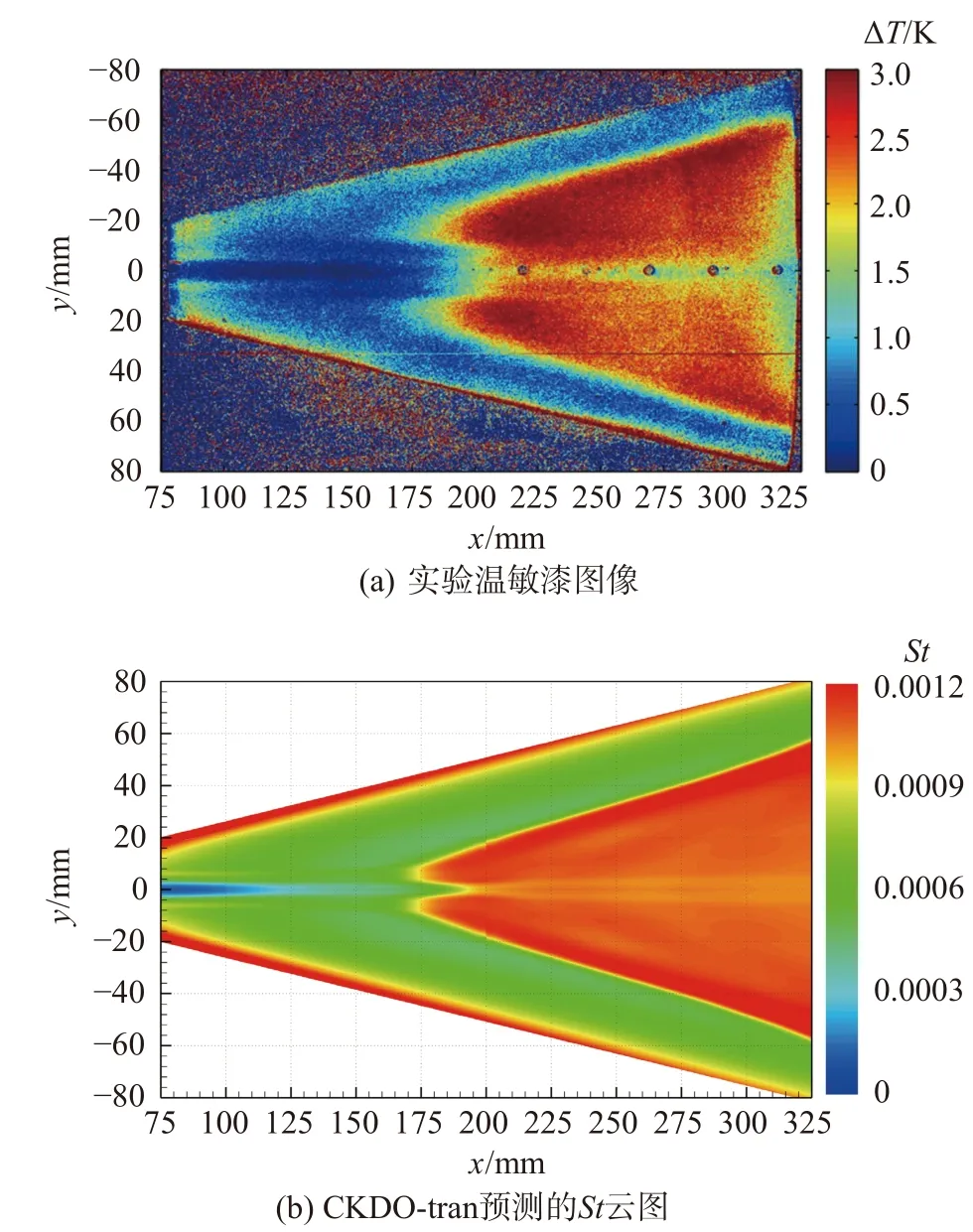
圖6 Case2 轉捩圖像Fig.6 Transition pattern of Case2

3.3 迎角效應

盡管實驗給出了帶迎角的HIFiRE-5 高超聲速轉捩工況，文獻中卻缺乏相應的轉捩模型研究，可見帶迎角的高超聲速轉捩具有一定挑戰性。本節在此進行Case4 計算評估，用以展示迎角效應、評估模型。

圖7 給出Case4 工況下，實驗溫敏漆顯示的轉捩圖像和CKDO-tran 計算的St云圖。轉捩圖像來自于HIFiRE-5 模型的迎風面，此時轉捩圖像從原來的雙肺葉形狀變成頂部帶尖角的鐘形。CKDO-tran 預測的轉捩圖像與實驗差距較大，主要是因為轉捩位置整體提前。然而，CKDO-tran 捕捉到的中軸線上的藍色細長泡、藍色細長泡上下方的細長泡（低溫區域）、以及隨后的鐘形及尖角，都與實驗圖像一一對應，表明CKDO-tran 預測的轉捩圖像與實驗具有相似性。向星皓等[9]對高超聲速尖錐橫流轉捩的計算，同樣發現了隨著迎角增大，計算的轉捩位置靠前、轉捩圖像相似但有所變形的現象。可見，真實情況的迎角效應是轉捩圖像變化；而湍流/轉捩模型的迎角效應，是隨著迎角增加，預測精度下降。

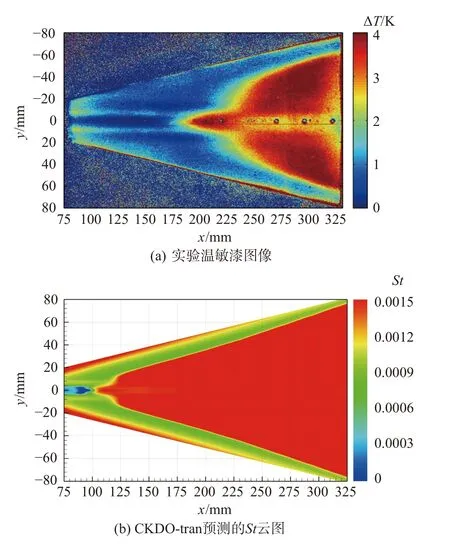
圖7 Case4 轉捩圖像Fig.7 Transition pattern of Case4

鑒于CKDO-tran 計算轉捩的機制是流動結構自適應自發捕捉，并已考慮可壓縮效應，變迎角導致的迎風面壓縮性變化不應導致如此大的計算誤差。鑒于各向同性湍流-正激波這種最簡單的湍流過激波問題，各種標準湍流模型的計算誤差都很大[21]，本文推測，誤差應來自來流湍流與頭部脫體激波的相互作用。兩者間的作用在迎角0°時導致的誤差尚可接受，一旦有迎角，湍流-激波作用的各向異性造成的波后湍流度不均勻性就會增強，反映在迎風面上的轉捩面的劇烈變化。因此，為了精準預測高超聲速橫流轉捩，需加強湍動能或間歇因子過激波過程的建模。通過改進來流湍流過激波的建模，也能提高轉捩模型對迎角0°工況的計算精度。

3.4 湍流度的影響

圖8 給出了湍流度對轉捩的影響。在前文，分析了湍流-激波作用的影響，認為湍流-激波作用建模的誤差，導致飛行器頭部感受到的來流湍流度失真,失真的湍流度造成失真的轉捩圖像。這一觀點成立的前提是，來流湍流度是影響轉捩的主要因素之一。事實上，轉捩圖像對湍流度的變化十分敏感，本節在此展示。仍然采用帶迎角的Case4 算例，僅變化其中的湍流度，形成工況Case5 和Case6，計算的轉捩圖像分別見圖8（a）和圖8（b）。可見，隨著湍流度的降低，CKDO-tran 計算的轉捩位置逐漸后移；轉捩圖像逐漸偏離實驗結果，與實驗圖像的相似性最終消失。

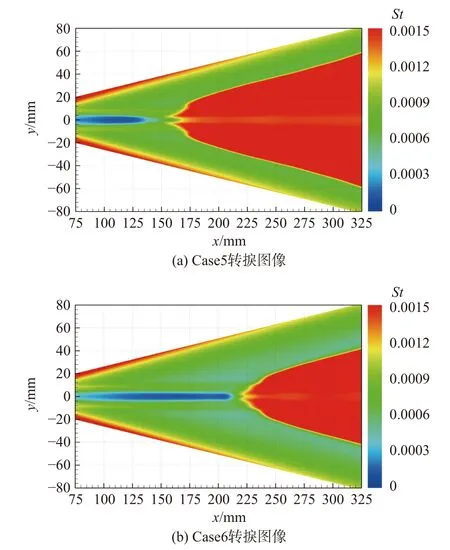
圖8 湍流度對轉捩的影響Fig.8 Effect of turbulence intensity on transition

4 結論

本文采用HIFiRE-5 經典標模，評估了CKDO-tran模型預測高超聲速橫流轉捩的性能，并研究了可壓縮因素、雷諾數因素和迎角因素對轉捩的影響。結論如下:

1）CKDO-tran 的高超聲速橫流轉捩預測精度顯著高于KDO-tran 模型，表明可壓縮效應的捕捉，對基于流動結構自適應的轉捩模型至關重要；

2）采用CKDO-tran 計算了迎角0°、多雷諾數的HIFiRE-5 標模，豐富了雷諾數工況，為他人研究提供了參考。計算得出的橫流轉捩與實驗符合較好，表明該模型對0°迎角的橫流轉捩具有較好的適用性；

3）4°迎角下，CKDO-tran 計算的橫流轉捩圖樣結構與實驗相似，但轉捩線過于提前，表明CKDO-tran對非0°迎角的高超聲速橫流轉捩的預測具有一定潛力，但仍需進一步完善該模型。

4）基于間歇因子γ的轉捩模型，用湍流模型提供全湍流解，用γ指示層流區域和轉捩區域。然而，γ方程里顯含k與μt，這正是來流k與μt影響轉捩位置的原理。基于γ的轉捩模型是有可能在k方程過激波計算失誤的情況下，通過調整γ方程的其他參數而獲得準確的預測結果的。因此，間歇因子轉捩模型的轉捩位置同時取決于湍流方程和γ方程。

本文完全通過湍流方程的演化捕捉轉捩，排除了γ方程的因素，所得的結論完全針對于湍流方程，可為各模型的湍流方程的改進提供可靠的信息，如需加強來流湍流過激波的研究等。