基于進化能力的多策略粒子群優化算法
王曉艷,曹德欣
中國礦業大學 數學學院,江蘇 徐州 221116
粒子群優化(particle swarm optimization,PSO)[1]算法是受鳥群捕食行為啟發提出的一種群體智能算法。該算法簡單、收斂快、魯棒性高、易于實現,已經在特征選擇[2]、移動機器人定位[3]、工程設計[4]等多個問題上被廣泛應用。然而,在算法后期,粒子常常被困于局部最優,從而過早收斂,因此研究人員從改進參數、增加種群多樣性、與其他智能算法結合等方向對粒子群算法進行改進。Shi和Eberhart提出線性遞減慣性權重[5],算法性能得到提升,之后又針對動態系統提出一種隨機調整慣性權重[6]的方法。文獻[7]設計了一種自適應慣性權重,并對群體最優引入混沌策略,從而避免粒子陷入局部極值。文獻[8]利用其他粒子的個體歷史最優來更新粒子的速度,以提高種群的多樣性。文獻[9]結合RMSProp算法中對學習率每個維度自適應調整的策略,設計自適應的慣性權重。文獻[10]對粒子的進化趨勢進行干預,減少隨機性,同時用個體最優指導群體最優在單個維度的學習,提高收斂精度。文獻[11]將遺傳算法、蟻群算法和粒子群算法相結合,提升算法的探索和開發能力。同時,有學者利用混合多種不同進化策略或學習機制的方式,取長補短,克服算法缺陷。文獻[12]中讓粒子根據歷史經驗和環境感知自適應選擇不同的進化策略。文獻[13]引入三洞系統捕獲策略提升種群多樣性,多維隨機干擾策略和早熟擾動策略提升算法精度。文獻[14]在簡化粒子群算法的基礎上融入基于相似度及聚集度分析的萊維飛行,幫助粒子逃離局部最優。這些措施對算法性能有一定程度的提升。
在粒子群算法中,整個種群都采用同一個進化策略,迭代后期就易出現多樣性不足,從而降低算法全局尋優能力。將種群分為多個子群,分別采取不同的學習機制,是一種較好的增加種群多樣性方式。文獻[15]將種群分為三個協同優化的子群,各個子群分別側重搜索不同的區域,實現算法性能提升。文獻[16]將粒子群分為多個子種群,并分別采取不同的DPPSO變體進化,子種群間以一定的遷移規則實現信息交流,提升算法穩定性。文獻[17]根據粒子適應值以及適應值均值和標準差將粒子所在區域分為拒絕域、親近域、合理域,并分別選取不同的慣性權重和學習因子。文獻[18]根據粒子適應值,在迭代過程中將粒子動態分為三個階層,并分別采取局部、標準、全局學習模型,增加種群多樣性。但是目前大多的分群策略都是依據粒子適應值的優劣進行的,對粒子的進化能力關注較少,導致算法較易陷入局部最優。
基于此,本文基于粒子的進化能力將粒子群分為不同子群,并融合多策略的思想,提出基于進化能力的多策略粒子群優化算法(EAMSPSO)。首先,在線性遞減慣性權重中引入隨機性,設計一種帶有隨機波動的慣性權重,使粒子在算法后期仍然具有跳出當前區域的能力,利于全局搜索。其次,將粒子按照進化能力分為進步粒子、暫時停退粒子、長久停退粒子,并依據不同子群的特性分別執行不同的進化策略,增加種群多樣性。
半無限規劃問題(semi-infinite programming,SIP)是數學規劃中的一類典型非光滑優化問題,是數學規劃中的一個重要研究分支,在最優控制、信息技術、交通問題等領域中有著廣泛的應用。但半無限規劃自身的特點和復雜性,給數值求解帶來困難。有學者利用精確罰
函數法[19]、濾波器信賴域方法[20]、區間算法[21]進行求解,取得了較好的結果。本文將EAMSPSO算法應用于半無限規劃問題的求解。
1 粒子群優化算法(PSO)
PSO算法由一個隨機種群開始,群體中的粒子均有自身的速度參數和位置參數,粒子通過追蹤自己在飛行過程中搜索到的最佳位置即個體最優,以及全部粒子經過的最優位置即群體最優,更新速度和位置,不斷迭代以達到最優。
設一個種群含有N個粒子,每個粒子是D維空間中的個體。對粒子i,用Xi=[Xi1,Xi2,…,XiD]表示粒子位置,用Vi=[Vi1,Vi2,…,ViD]表示飛行速度,個體最優位置用pbest表示,群體最優位置用gbest表示。速度和位置更新方程是:
其中,t為當前迭代次數,w為慣性權重,c1、c2為學習因子,r1、r2為(0,1)間均勻分布的隨機數。
2 基于進化能力的多策略粒子群優化算法(EAMSPSO)
2.1 慣性權重
文獻[5]中說明,在算法中慣性權值能夠協調局部、全局搜尋能力。慣性權重較大,對于初始種群的依賴較小,粒子發現新領域的能力較強,利于全局搜索;反之,若慣性權重較小,算法則更趨向局部搜尋。對于線性遞減的慣性權重,每代所有粒子的慣性權重都一樣,粒子的慣性權重在算法后期都較小,如果初步搜尋到的領域中包含全局最優解,粒子可以較迅速地聚攏至全局最優,相反如果前期搜索到的區域不存在全局最優解,那么在迭代后期粒子失去了跳出當前區域的能力,就會陷入局部極值。針對這一問題,在線性遞減策略中引入隨機性,同時考慮不同粒子的位置的優劣,給予位置較優的粒子較小的慣性權重,位置較差的粒子較大的慣性權重,設計一種帶隨機波動的慣性權重,如下:
其中,t為當前迭代次數,T為總迭代次數,wmax、wmin為線性遞減慣性權重的最大、最小值。r[1,E]是[1,E]上的隨機整數,其中E是一個整數,E的大小決定波動的程度。ranki是粒子i的歷史最優在整個種群中的位次,個體最優位置越好,排序越靠前,位次越小。
改進后的慣性權重總體呈減小趨勢,但是存在一定的隨機波動。前期較大的慣性權重能夠使得粒子在初期進行廣泛的搜尋,同時后期也有一定的概率獲得比較大的慣性權重,從而使粒子具有跳出局部極值的能力。
2.2 改進粒子進化方式
定義1粒子i在第t(t≥2)代的適應值變化定義為:
當ΔF(Xit)<0時,說明粒子按照當前方向移動,適應值下降,即粒子處于進步狀態,當前的速度仍然具有可參考性。反之,說明粒子按照當前方向移動,適應值沒有變好反而變差了,當前速度方向的可參考性降低。
定義2粒子i在第t(t>d,d>1)代的粒子活性定義為:
當dF(Xit)<0時,說明粒子位置對比d代前更好,反映出粒子仍然存在活性,否則說明粒子位置有可能連續d代無優化,粒子已經失去活性。
PSO算法中所有粒子都按照式(1)、(2)更新速度、位置,沒有考慮到不同表現的粒子的差異性,導致進化后期,容易出現多樣性丟失,從而早熟收斂。考慮到這一問題,本文在每次迭代中,根據適應值的變化將粒子分為進步粒子和停止或者退步的粒子簡稱停退粒子。針對停退粒子進一步根據粒子活性分為暫時停退粒子和長久停退粒子,并根據不同類型粒子的特點采取不同的進化策略。
2.2.1 進步粒子
進步粒子即適應值下降的粒子,說明粒子當前在沿著正確的方向移動。因此,粒子應該參考過去的經驗繼續前進。進步粒子采用原算法中粒子的進化方式,通過參考上一代中的速度,并追隨個體歷史最優和全局最優進行更新,保留原算法的優點。
2.2.2 暫時停退粒子
暫時停退粒子即d代內粒子的位置沒有變好,說明粒子當前的速度方向可能需要調整。針對暫時停退的粒子,減小對歷史速度的參考,或者對其進行反向參考。更新方式按照式(6)、(2)。
其中,ε是為了減小或者反向對歷史速度的參考而引入的調節因子。
2.2.3 長久停退粒子
長久停退粒子即超過d代(含d代)粒子的適應值沒有變好。對于這些粒子分為兩種情況進行討論,一類是個體最優對應的適應值較優的粒子,這類粒子可能已經陷入局部最優,如果仍然按照原始進化策略更新會導致粒子停滯在局部最優。同時,這類粒子的適應值較優說明它們占據的位置較好,靠近最優解的概率相對較大,因此這類粒子以一定的概率在個體最優位置周圍進一步搜索,或者沿著全局最優的方向搜索。具體更新方式按照式(7)、(8):
其中,β、α、γ是服從(0,1)正態分布的隨機數,pa表示在個體最優周圍搜索的概率,1-pa為沿全局最優方向搜尋的概率。
另一類是個體最優對應的適應值相對較差的粒子,這類粒子本身占據的位置相對較差,而且適應值沒有下降,說明這類粒子的位置和速度均需要重新調整,讓這類粒子直接由個體歷史最優出發,向群體最優方向進行搜索。具體的更新方式如式(9)、(8)。
其中,r是(0,1)之間均勻分布的隨機數。
2.3 EAMSPSO算法
根據2.1和2.2節的介紹,提出基于進化能力的多策略粒子群優化算法(EAMSPSO),算法的具體執行流程在圖1中展示。
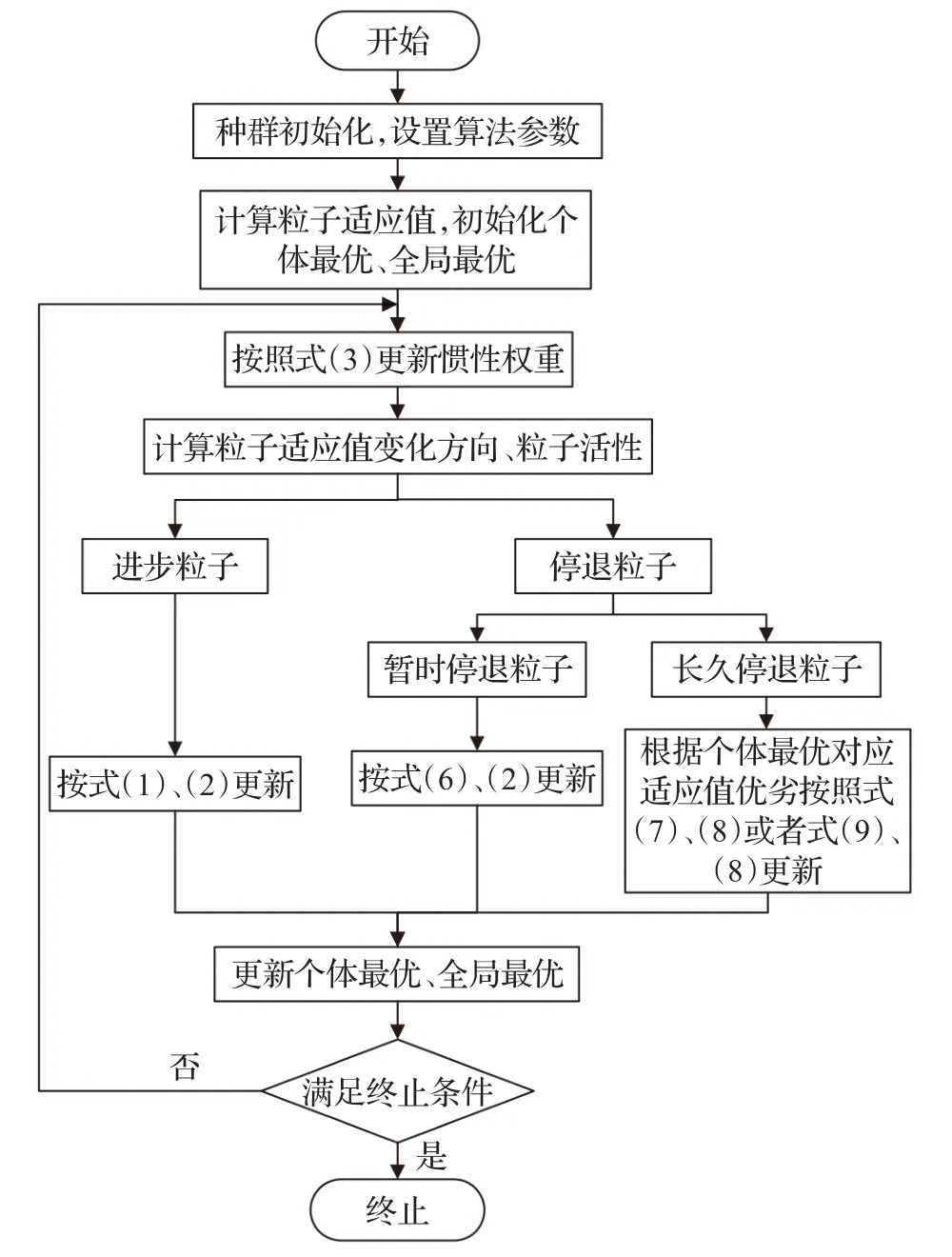
圖1 算法執行流程Fig.1 Algorithm execution flow
算法EAMSPSO
輸入:種群規模N、總迭代次數T
輸出:gbest
1.隨機初始化N個粒子;
2.計算粒子適應值;
3.初始化gbest;
4.Whilet 5.Fori=1 toNdo 6.按照式(3)更新慣性權重; 7.若t>2按式(4)計算ΔF(Xit-1)否則為-∞; 8.若t>d+1按式(5)計算dF(Xit-1)否則為-∞; 9.IfΔF(Xit-1)≥0 10.IfdF(Xit-1)≥0 11.根據個體最優對應適應值的優劣按照式(7)、(8)或式(9)、(8)更新; 12.Else 13.按照式(6)、(2)更新速度、位置; 14.End if 15.Else 16.按照式(1)、(2)更新速度、位置; 17.End if 18.更新pbest、gbest; 19.End for 20.End while 21.Returngbest 在PSO算法里,設共N個粒子,粒子維數為D,共迭代T次。算法時間復雜度主要體現在種群初始化以及粒子速度、位置、適應值更新上。假設計算粒子適應度值的時間為f(D),則種群初始化的復雜度是O(ND+Nf(D)),進行粒子更新的復雜度為O(TND+TNf(D)),算法總時間復雜度為O(TN(D+f(D)) )[14]。 在EAMSPSO算法中,種群初始化的復雜度仍然為O(ND+Nf(D))。每次迭代,首先要計算粒子的適應值變化方向和粒子活性,該過程的時間復雜度為O(N)。其次,粒子被分為進步粒子、暫時停退粒子、長久停退粒子三類分別更新,設每次迭代進步粒子的個數為n1,暫時停退粒子的個數為n2,長久停退粒子的個數為n3,那么n1+n2+n3=N。在每次迭代中,進步粒子、暫時停退粒子、長久停退粒子更新的時間復雜度分別為O(n1D+n1f(D))、O(n2D+n2f(D))、O(n3D+n3f(D)),所以種群更新一次的時間復雜度是O(n1D+n1f(D))+O(n2D+n2f(D))+O(n3D+n3f(D))=O(ND+Nf(D))。此外,對于長久停退粒子需要根據個體最優的適應值優劣分別采取不同的更新策略,因此在每次迭代時,需要將粒子根據個體最優位置的適應值進行排序,排序過程的時間復雜度為O(N2)。綜上可知,每次迭代中包含粒子適應值變化方向和粒子活性計算、粒子更新、排序三個步驟,時間復雜度分別是O(N)、O(ND+Nf(D))、O(N2),當粒子的維度比較小的時候,粒子維度與種群規模接近,當粒子的維度適中或較大時,種群規模接近或者小于粒子維度,所以算法總體復雜度近似為O(TN(D+f(D)))。 本文通過10個基準函數測試EAMSPSO算法性能。 (1)Sphere函數 (2)Schwefel 2.22函數 (3)Rotated Hyper-Ellipsoid函數 (4)Sum of Different Powers函數 (5)Zakharov函數 (6)Griewank函數 (7)Rastrigin函數 (8)Ackley函數 (9)Quartic函數 (10)Shubert函數 其中,函數f1~f9的理論最優均為0,f10理論最優為?186.730 9。f1~f5、f9是單峰函數,f6~f8、f10是多峰函數。 實驗在MATLAB軟件環境下進行,算法的粒子規模設為40,算法最大迭代次數設為2 000。EAMSPSO算法中c1=c2=2,粒子活性的評估間隔d取為3。ε取為(0,0.5)之間的隨機數,使得暫時停退粒子可以減小對歷史速度的參考,在進化后期還存在一定的可能對歷史速度進行反向參考。個體最優適應值較優粒子的比例取為1/3。為了平衡算法的探索和開發能力,使長久停退的個體最優適應值較優的粒子以相同的概率在個體最優周圍搜索和沿全局最優方向搜尋,因此pa取為50%。 本文采用帶隨機波動的慣性權重,以使粒子可以跳出局部最優,從而提高算法性能。針對慣性權重中的參數wmax、wmin、E,本文設置以下幾組參數,并在函數f2和f9上進行實驗對比。不同的參數組合均獨立運行30次,實驗結果在表1中展示。從表1中的數據可以看出,wmax為0.8,wmin為0.3,E的值取為5時,其實驗效果最好。所以本文wmax取0.8,wmin取0.3,E取為5。 表1 慣性權重的參數對比Table 1 Parameter comparison of inertia weights 為了測試算法的性能,通過3.1節中的10個基準測試函數測試EAMSPSO算法性能,并與線性遞減慣性權重粒子群優化算法(LPSO)[5]、綜合學習粒子群優化算法(CLPSO)[8]、具備自糾正和逐維學習能力的粒子群算法(SCDLPSO)[10]、粒子群優化與灰狼優化的混合算法(HPSOGWO)[22]進行對比實驗。LPSO、SCDLPSO算法中c1=c2=2,w:0.9~0.4,CLPSO算法中c=1.494 45,w:0.9~0.4,HPSOGWO算法中c1=c2=c3=0.5,w=0.5+rand()/2。5種算法分別在10個測試函數上獨立運行30次。 3.3.1 算法在低維函數上的實驗 將基準測試函數f1~f9的維度設置為30維,5種不同算法對10個函數的優化結果,包括各個算法獨立運行30次得到的平均值、最大值和標準差,在表2中展示。其中,加粗的結果為對比實驗中最好的結果。5種算法在10個測試函數下的適應度值變化趨勢對比在圖2中展示。 3.3.2 算法在高維函數上的實驗 利用單峰函數f1、f2和多峰函數f6、f8測試EAMSPSO算法對于高維問題的優化性能,將這4個函數維度設置為100維。各個算法對函數優化30次的平均值在表3中展示。 表3 五種算法對高維測試函數的實驗結果對比Table 3 Comparison of experimental results of five algorithms on high-dimensional test functions 當測試函數維度較低時,由表2中的結果可以看出,在單峰函數上,對于函數f1、f3、f4、f5,本文算法EAMSPSO均可收斂到理論最優,其他算法在迭代次數內均未達到理論最優。對于函數f2和f9,本文算法及對比算法均未能收斂到理論最優,但是從表2和圖2中可看出,相比其他對比算法,EAMSPSO算法找到的解相對更優。多峰函數具有多個局部極值,求解困難度較高,對于函數f6、f7,本文算法EAMSPSO與算法HPSOGWO可以找到最優值,其他算法在迭代次數內未達到理論最優,而且從圖2中可以看出算法EAMSPSO的收斂速度快于算法HPSOGWO。對于函數f8,所有算法均未收斂到理論最優,但從表2中的求解結果和圖2中的收斂曲線可以看出,算法EAMSPSO的求解精度和收斂速度均優于其他算法。多峰函數f10理論最優非零,本文算法EAMSPSO和算法LPSO、CLPSO、SCDLPSO均可以找到最優解,從求解的標準差來看本文算法的穩定性更好。 圖2 低維函數不同算法的適應值變化趨勢對比圖Fig.2 Comparison chart of fitness value change trend of different algorithms for low-dimensional functions 表2 五種算法對低維測試函數的實驗結果對比Table 2 Comparison of experimental results of five algorithms on low-dimensional test functions 當測試函數設置為100維時,對于函數f1、f6算法EAMSPSO仍然可以找到最優解,對于函數f2、f8五種算法均未到達理論最優,但是相比對比算法,EAMSPSO算法求解的精度更高。可見本文提出的EAMSPSO算法不僅對低維問題的優化效果較好,對于高維問題的求解同樣具有優勢。 數值結果表明,本文提出的EAMSPSO算法可以有效地跳出局部極值,且算法的穩定性較高。對無論是低維還是高維函數,單峰還是多峰函數,EAMSPSO算法求解精度和收斂速度上都具備優勢。 本文所研究的半無限規劃問題具體表達形式如下: 其中,X(0)={x=(x1,x2,…,xn)T∈Rn},f:Rn→R,?i:Rn×Rpi→R。 利用罰函數問題(11)可以轉化為無約束優化問題(12): F(x,β)=f(x)+βq(x),q(x)=max{0,h(x)},β為罰因子,當罰因子足夠大時問題(12)的解就是問題(10)的解。 本文采用EAMSPSO算法求解半無限規劃問題(10),即求解問題(12)。當給定罰因子后,F(x)是關于x的函數,算法中粒子位置即x,粒子適應值即F(x)函數值。該問題的難點在于適應值的計算,F(x)計算中包含一個求解最大值的子問題即對h(x)的計算: 計算過程中需要對m個求最大值的問題進行求解。當x給定時,?i(x,t)即為關于t的函數。每個求最大值問題都可以轉化無約束優化問題(13)的形式。 針對無約束優化問題(13),同樣可以采用EAMSPSO算法進行求解。 將EAMSPSO算法應用于半無限規劃問題1~5的求解,并與3.3節中的對比算法進行對比,各個算法參數與3.3節保持一致。求解半無限規劃問題時,算法粒子規模設為40,最大迭代次數設為500,每個算法獨立運行5次求平均值。同時每個適應值的計算包含的求最值問題,采用同樣的算法進行計算,種群規模設為40,最大迭代次數設為100。數值結果在表4~8中展示。 表4 問題1的計算結果Table 4 Calculation result of question 1 表5 問題2的計算結果Table 5 Calculation result of question 2 表6 問題3的計算結果Table 6 Calculation result of question 3 表7 問題4的計算結果Table 7 Calculation result of question 4 表8 問題5的計算結果Table 8 Calculation result of question 5 問題1[23]: Subject to?(x,t)=x12+2x2t2+ex1+x2-et≤0,t∈[0,1] 最優解為(0.719 961,?1.450 487)。 問題2[23]: 最優解為(-ln 1.1,ln 1.1)。 問題3[24]: 最優解為(0,0,0)。 問題4[25]: 最優解為(?1,0,0)。 問題5[25]: 最優解為(3,0,0,0,0,0)。 問題1、2、3中,t是一維變量,問題4、5中t是二維變量。從實驗結果可以看出,對于問題1、問題2和問題4,算法EAMSPSO可以找到最優解,其他對比算法均未找到最優解,而且從函數值來看,對比算法求得的函數值小于算法EAMSPSO,說明對比算法在求適應值中包含的最大值問題時存在未達到最優的情況。問題3的目標函數不可微,本文算法EAMSPSO及對比算法在迭代次數內均未達到理論最優,但從求解結果可以看出,本文算法的求解精度更高。對于問題5,五種算法均未找到理論最優,CLPSO算法的求解結果最優,其次是本文算法EAMSPSO。可見,EAMSPSO算法適用于半無限規劃問題的求解,且具有一定的優勢。 本文提出了基于進化能力的多策略粒子群優化算法(EAMSPSO)。該算法設計了帶隨機波動的慣性權重,可以使粒子在進化后期也具有跳出當前區域的能力。將粒子群按照適應值變化方向和粒子活性分為進步粒子、暫時停退粒子、長久停退粒子,并分別采取不同的進化策略,提高全局尋優能力。實驗結果表明,EAMSPSO算法在求解精度和收斂速度上都具備優勢。同時,將EAMSPSO算法應用于半無限規劃問題的求解,進一步驗證了改進算法的有效性。2.4 算法的時間復雜度分析
3 性能測試
3.1 測試函數
3.2 參數設置
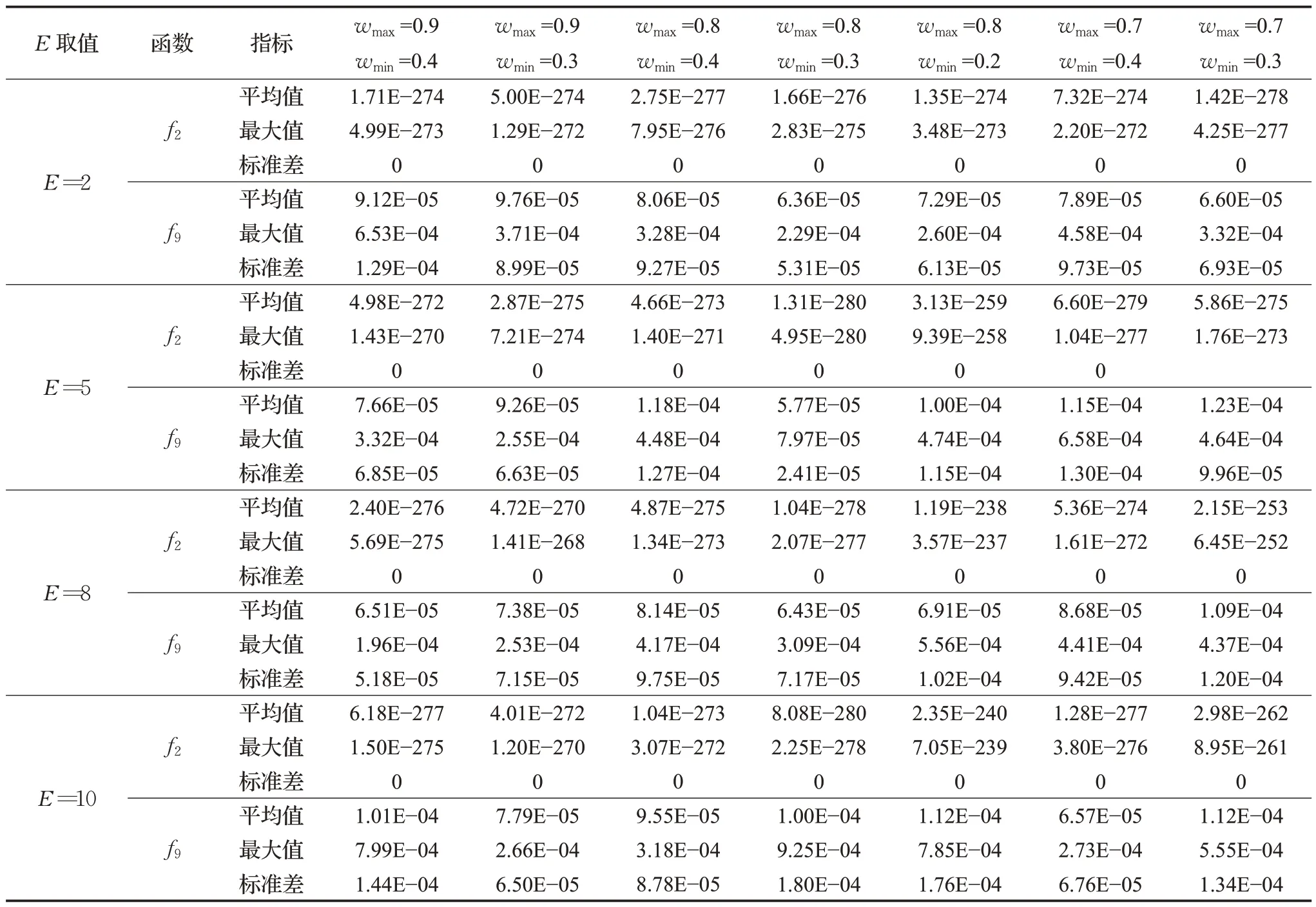
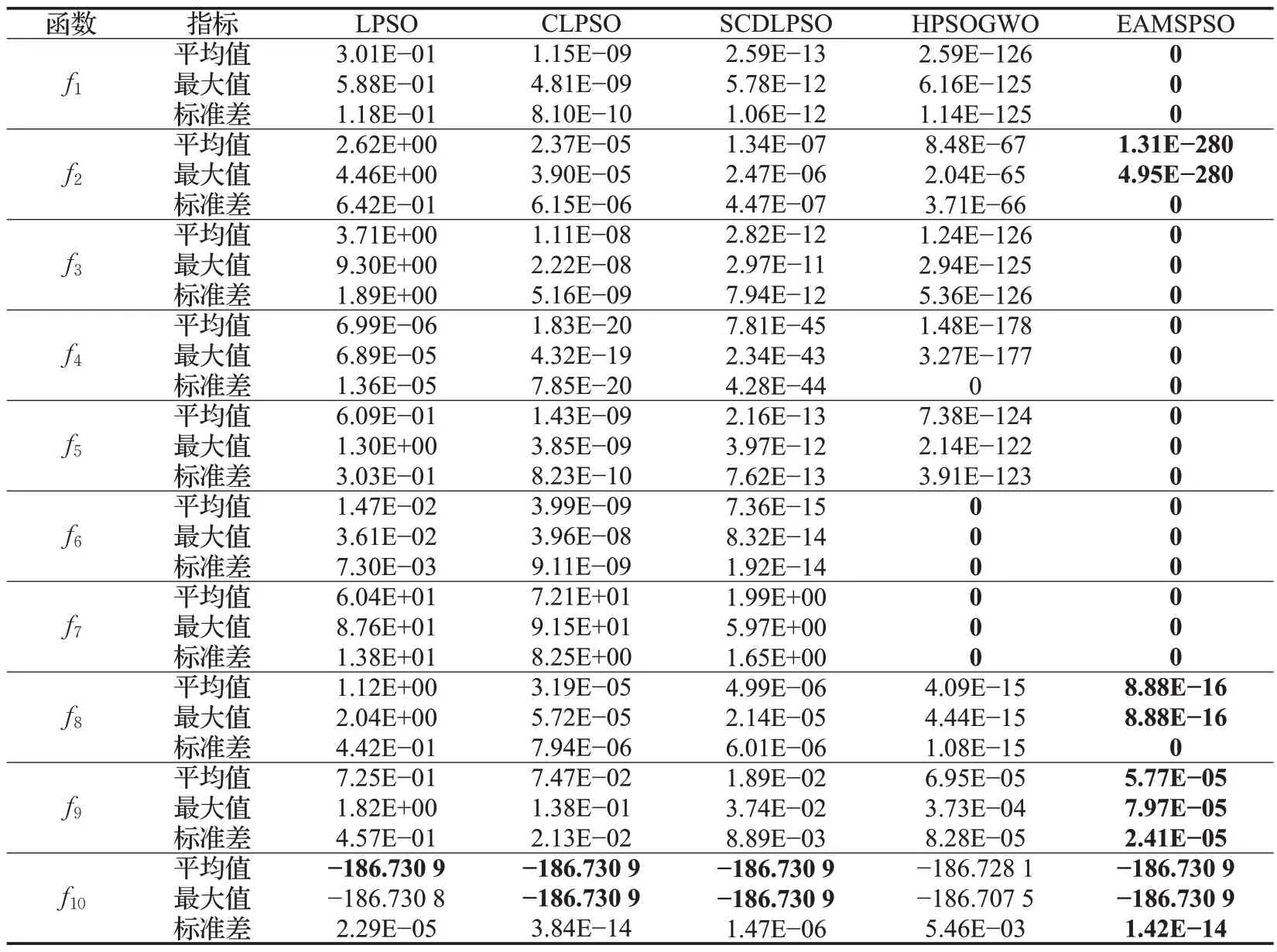
3.3 數值實驗
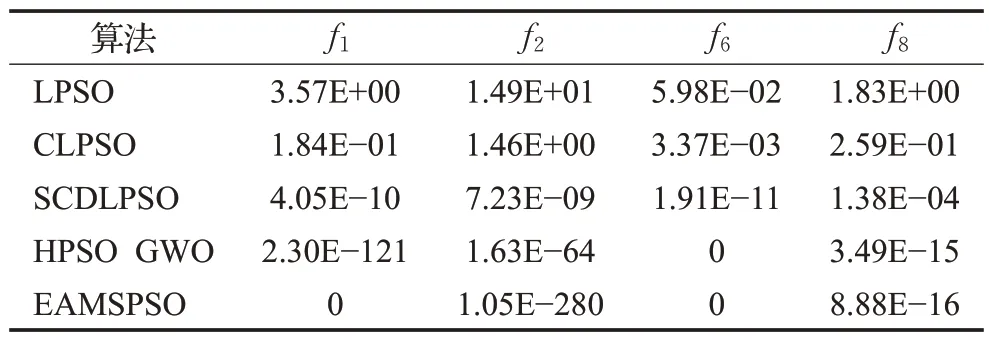
3.4 結果分析
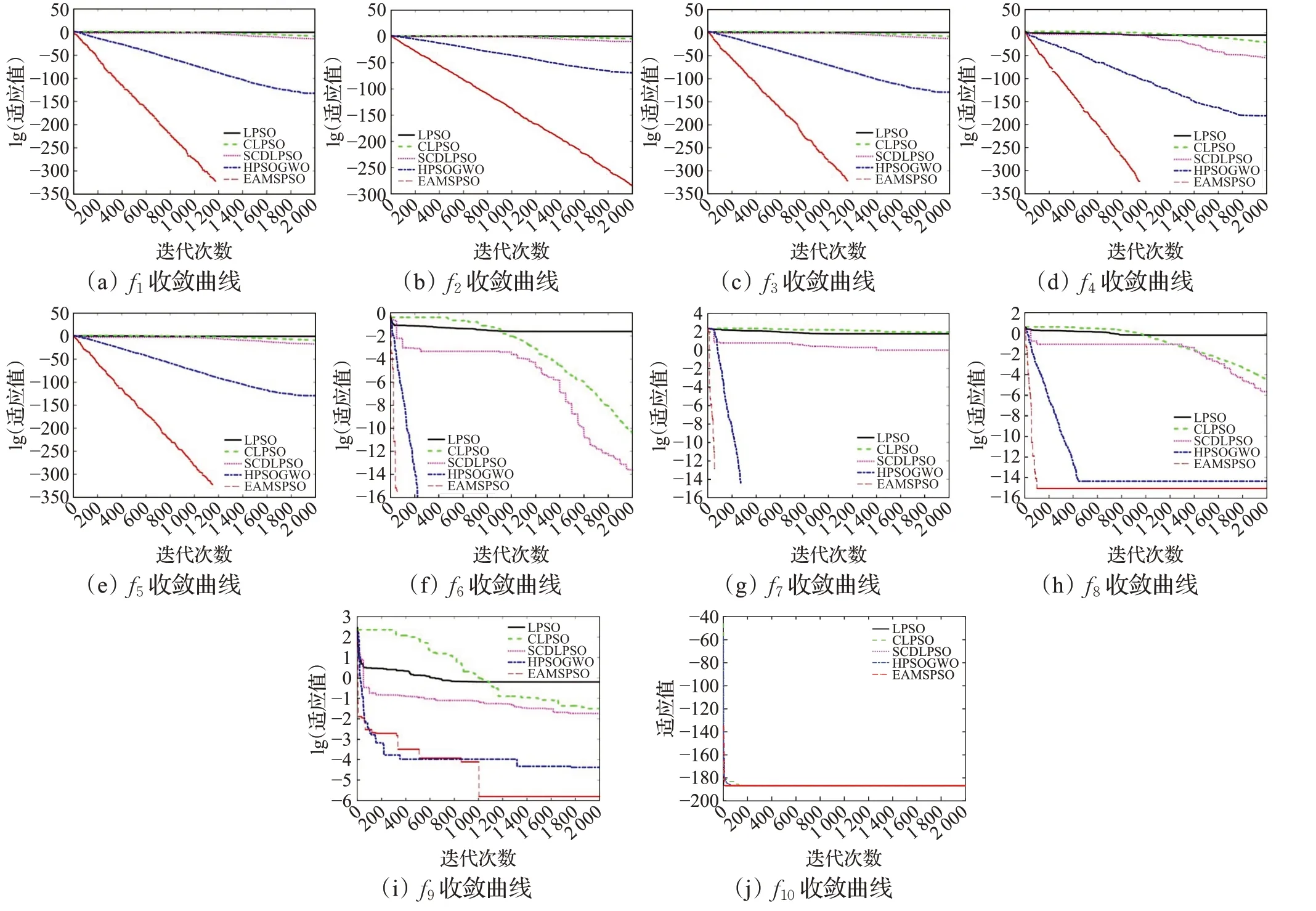
4 EAMSPSO算法求解半無限規劃問題
4.1 問題描述及算法
4.2 數值實驗
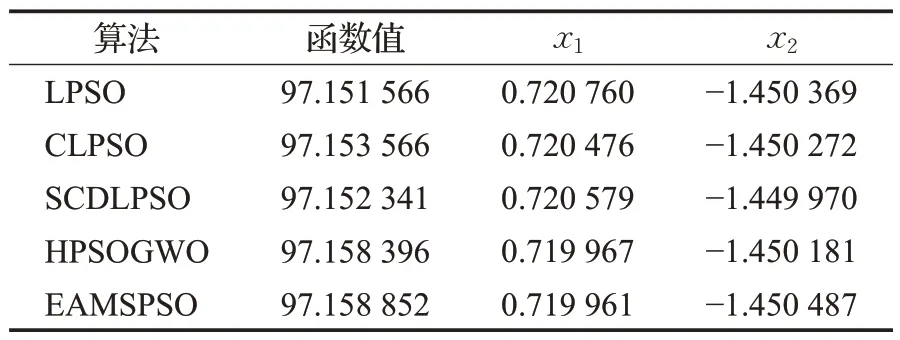
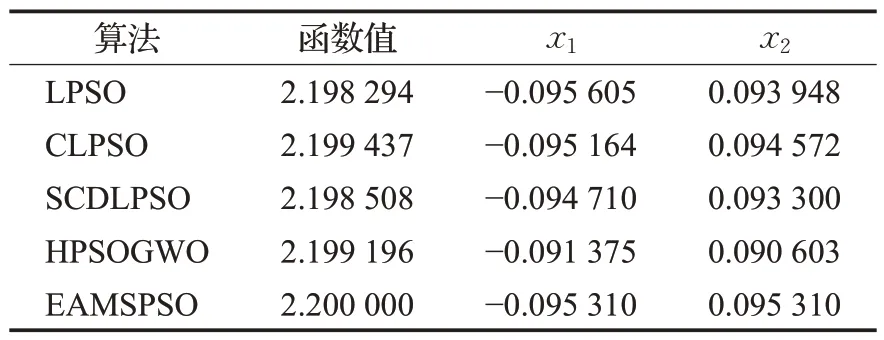
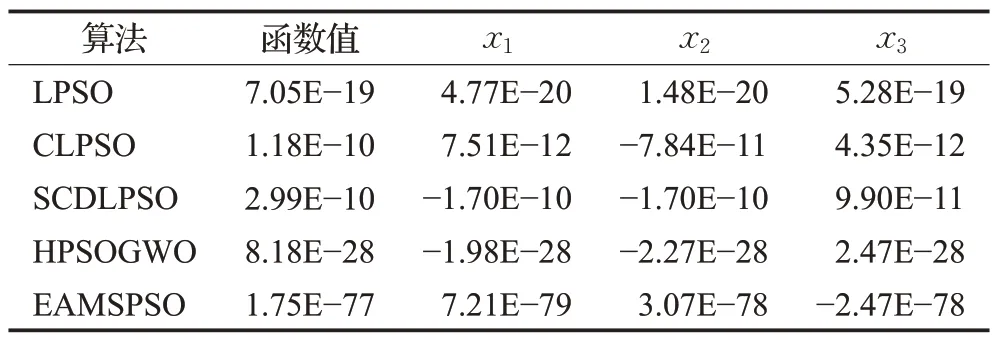
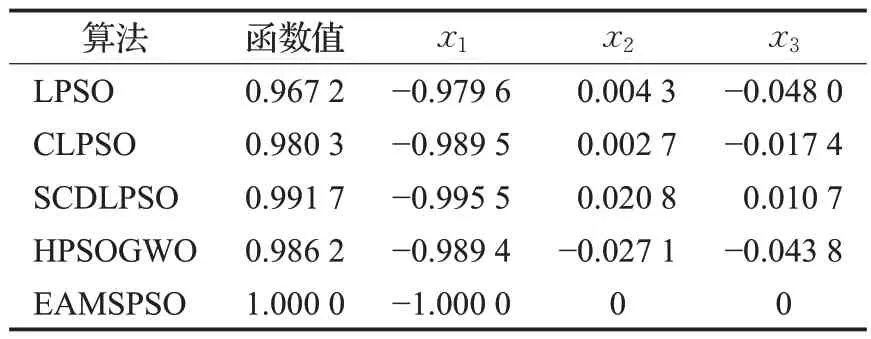
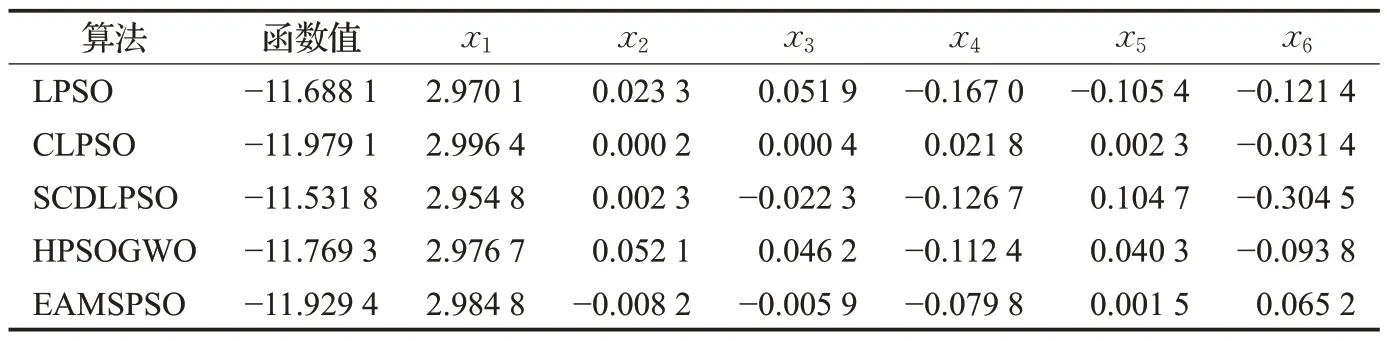
4.3 結果分析
5 結束語

