基于PDE靈敏度濾波器的算法研究*

孟換利，張岐良，王 杰

（1.中山大學 系統科學與工程學院，廣州 510006；2.天津航天長征火箭制造有限公司，天津 300462）

引言

為應對越來越高的力學性能要求和越來越嚴酷的服役環境，在結構設計中應用拓撲優化技術已成為一種必然選擇.在結構的概念設計階段通過結構拓撲優化確定材料的最優布局形式，可以幫助設計者發現結構最佳的應力傳導路徑，從而以最少的材料實現最優的結構性能.Deaton 和Grandhi[1]調查了2000年至2012年連續體結構拓撲優化的研究現狀與應用.Zhu 等[2]綜述了面向增材制造的拓撲優化技術的典型應用場景、研究熱點和挑戰.衛志軍等[3]對雙隔板進行了拓撲優化，可以有效地抑制流體晃蕩.

然而，連續體結構的拓撲優化結果往往存在棋盤格現象、數值不穩定等問題，Sigmund[4]以及Bruns、Tortorelli[5]使用的靈敏度濾波器和密度濾波器可以有效地解決上述問題.研究者們在此基礎上發展了多種過濾方法，如灰度單元等效轉換方法[6]、動態參數調整方法[7]和灰度單元分層雙重懲罰方法[8]等.上述方法在一定程度上可以有效地抑制灰度單元、消除棋盤格現象，防止邊界灰度擴散，但沒有關注過濾效率.與通過獲取鄰域的單元信息來修正中心單元的靈敏度濾波器不同，PDE 濾波器的實質是將靈敏度過濾值表示成Neumann 邊界條件下的Helmholtz 方程的解，其求解只需考慮有限元離散的網格信息，避免了占用大量內存，極大地提高了過濾效率.然而隨著網格的不斷細分，該濾波器的代數方程維數越來越高，采用以Gauss 消元法為基礎的直接法求解，會導致耗時過長和內存需求量增加等問題，從而影響該濾波器的效率.此外，隨著計算機性能的提高和算法技術的發展，精細的數值模擬成為可能，使得待求解的線性方程組的維數越來越高，研發高效的線性求解器加速算法[9-11]已變得至關重要.

多重網格是一種高效的求解算法，近期在偏微分方程參數反演問題方面有許多應用[12-13]，并廣泛地應用到圖像處理[14]、流體模擬[15]和結構拓撲優化[16-17]等領域.為提高大規模結構拓撲優化靈敏度過濾的效率，本文基于體積約束下柔度值最小的固體各向同性懲罰微結構(SIMP)插值模型，針對大規模PDE 靈敏度濾波器的求解問題，對其進行有限元分析得到代數方程，再采用共軛梯度算法、多重網格算法以及多重網格預處理共軛梯度算法進行求解，得到了過濾域的節點靈敏度值，通過節點到單元的映射得到了單元靈敏度過濾值.

1 優化模型

在變密度法中，SIMP 模型是目前工程領域應用最廣泛的材料插值模型，為了使模型更具有代表性，基于SIMP 插值模型，建立在體積約束下柔度值最小的連續體結構拓撲優化模型：

其中，目標函數C為結構的總體柔度，F為力向量，U為位移，K為結構的總剛度矩陣，xi和ui是第i個單元的相對密度和節點位移，ki和k0是單元剛度矩陣，V是優化后的結構體積，V?為結構體積約束，V0為整個設計域的初始體積，f為優化體積比，vi為第i個單元的體積，xmin和xmax為單元相對密度的最小和最大極限值，N為結構離散單元總數.

SIMP 法又稱冪律法，其材料插值模型以密度為設計變量，單元材料彈性模量和密度之間的關系為

其中E0和Emin是固體和空洞部分的材料彈性模量，Ei為第i個單元插值后的彈性模量.

2 拓撲優化算法

2.1 總體框架

連續體結構拓撲優化實現流程如圖1所示.首先，初始化優化參數：定義問題的設計區域、約束和載荷.其次，建立有限元模型：劃分有限元網格，將結構離散化，建立式(1)所示的連續體結構拓撲優化數學模型.另外，有限元分析：計算剛度矩陣、節點位移、目標柔度值和靈敏度.之后，PDE 靈敏度過濾：解決數值不穩定問題和消除棋盤格現象.然后，采用二分法和OC 準則更新Lagrange 乘子和設計變量，判斷是否滿足體積約束條件：滿足則輸出設計變量；若不滿足，則回到上一步再次更新Lagrange 乘子和設計變量.最后，檢查是否滿足收斂準則：若滿足，則輸出拓撲優化結果；若不滿足，則再次進行有限元分析，進行下一輪迭代.

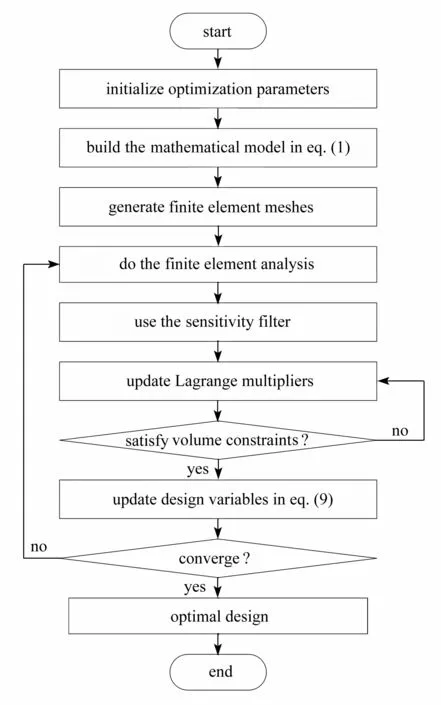
圖1 基于SIMP 插值模型連續體結構拓撲優化實現流程圖Fig.1 The flow chart of continuum structure topology optimization based on the SIMP interpolation model

為解決傳統PDE 靈敏度濾波器過濾慢的問題，本文采用共軛梯度算法求解該濾波器的對稱正定代數方程，為進一步解決網格數量增加導致系數矩陣維數增加和趨近最優解時，該算法收斂速度減緩的問題，結合多重網格可以均勻衰減誤差，加快算法收斂速度的優點，使用多重網格算法和預處理共軛梯度算法求解該方程，提升過濾效率.此外，在預處理共軛梯度算法中，采用多重網格預處理降低系數矩陣的條件數.

2.2 PDE 靈敏度濾波器

本文采用PDE 靈敏度濾波器[18-19]，其核心思想是將過濾域的節點靈敏度值隱式表示為具有Neumann 邊界條件的Helmholtz 方程的隱式解，然后通過節點到單元的映射得到單元靈敏度過濾結果：

2.3 PDE 靈敏度濾波器的求解

PDE 靈敏度濾波器的實質是以Neumann 邊界為條件的Helmholtz 偏微分方程，其求解步驟如下：

第1 步 有限元離散得到Helmholtz 方程(3)的代數方程：

其中KF是標量問題的標準有限元剛度矩陣，TF是將單元相對密度映射到具有節點值的向量的矩陣.針對代數方程(5)的系數矩陣是對稱正定稀疏病態的特點，本文擬采用共軛梯度算法、多重網格算法和多重網格預處理共軛梯度算法求解該代數方程，從而得到過濾區域內的節點靈敏度值.

第2 步 通過對過濾域的節點靈敏度值映射得到單元靈敏度過濾值：

2.3.1 多重網格算法

在固定網格中采用常規的迭代方法求解線性方程組，初始時收斂速度很快，趨近最優解時，收斂速度慢，計算時間長.采用Fourier 級數表示誤差，得到兩種不同的誤差：波長較短、波形頻率高的高頻分量誤差和波長較長、波形頻率低的低頻分量誤差.由于波形頻率的高低是相對的，把細網格中的低頻波形放到粗網格中就有可能變成高頻波形.因此采用多重網格來消除誤差分量，使各種頻率的誤差得到比較均勻的衰減，從而加快迭代收斂速度.假設有L重網格，k=1 為最細的網格層，在k層上的多重網格迭代解，多重網格V 循環具體過程如下（偽代碼見算法1）：

步驟1 前光滑.采用常規的迭代方法消除誤差高頻分量，具體步驟為：在細網格上，采取2 ～ 3 次的阻尼Jacobi 迭代方法得到線性方程組的近似解.迭代公式的通式為

其中Sk為光滑子，Sk=ωDk，ω 為阻尼因子，Dk為Ak的主對角元素矩陣.

步驟2 粗網格校正.計算在粗網格上誤差的近似解，具體步驟為：首先計算細網格上的殘差然后使用限制算子把細網格上的殘差限制到粗網格上，得到粗網格上的殘差最后根據網格的層數求解線性方程組得到粗網格上誤差的近似解，若是最粗的網格層，則利用直接法求解否則利用多重網格V 循環求解其中粗網格算子Ak+1取Galerkin 算子.

步驟3 插值.計算細網格上的解，具體步驟為：先使用插值算子把粗網格上的近似誤差插值到細網格上然后使用公式得到在細網格的解.本文采用的插值算子為

步驟4 后光滑.為保證整個迭代對稱，在細網格上，采取具有相同參數的阻尼Jacobi 迭代法求解線性方程組.

算法1

2.3.2 多重網格預處理共軛梯度算法

考慮到代數方程的系數矩陣是大型、稀疏、對稱正定的，有時甚至為病態的，則重點研究了多重網格預處理共軛梯度算法（偽代碼見算法2），采用多重網格作為預處理方法降低系數矩陣的條件數.

算法2

2.4 設計變量的更新

優化準則法（OC 準則）具有收斂速度快、易于實現等特點.本文采取OC 準則求解優化模型(1)，基本思路為，先引入Lagrange 乘子把約束問題(1)轉化為無約束問題，再根據極值點存在的條件即K-T 條件以及不動點迭代得到設計變量的迭代公式為

2.5 收斂準則

包括外循環和內循環，外循環包括有限元分析和更新單元靈敏度，迭代收斂條件如下：

內循環包括更新設計變量、Lagrange 乘子和過濾域的節點值.采用二分法和OC 準則更新Lagrange 乘子和設計變量，以滿足模型(1)中的體積約束和設計變量的邊界約束，迭代收斂條件如下：

其中η為收斂控制因子，l2和l1為較大和較小的Lagrange 乘子.采用共軛梯度算法、多重網格算法以及多重網格預處理共軛梯度算法求解代數方程，構造迭代收斂準則為

其中τ為收斂控制因子，rk和r0為第k次和初始時代數方程的殘量.

3 數值算例

為了驗證本文拓撲優化方法的可行性、可靠性和高效性，針對長960 mm、高320 mm 的懸臂梁和長960 mm、高480 mm Michell 結構的棋盤格現象、數值不穩定、靈敏度過濾慢等問題開展了數值實驗，如圖2 和3所示（算例優化參數為體積約束比為0.5、彈性模量為1 GPa、Poisson 比為0.3、懲罰因子為3、移動極限為0.2、外載荷F為1 kN）.拓撲優化程序基于文獻[16,20]的MATLAB 代碼進行編寫，在PDE 濾波器的求解中引入了共軛梯度（CG）算法、多重網格（MG）算法以及多重網格預處理共軛梯度（MGCG）算法，并比較了三種算法對結構拓撲優化效率的影響，相關數值結果如下.

圖2 懸臂梁Fig.2 The cantilever beam

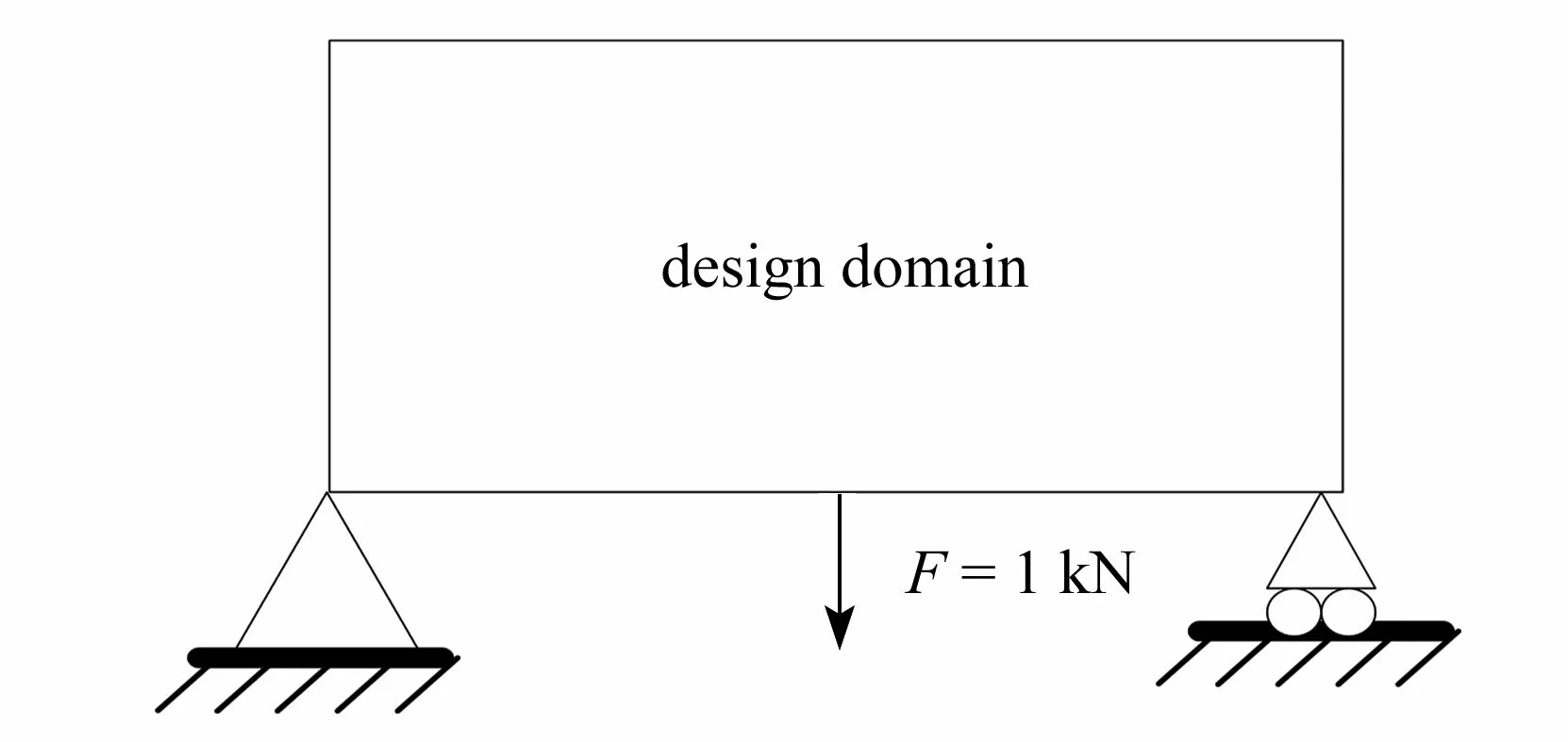
圖3 Michell 結構Fig.3 The Michell structure

3.1 精度的影響

依次取4 種不同的誤差精度P(P=1E–2,1E–3,1E–4,1E–5)，采用CG 算法、網格層數為5 的MG 算法和MGCG 算法求解經有限元分析Helmholtz 方程得到的代數方程，并對整個結構分別劃分為480×160和480×240個單元的懸臂梁和Michell 結構進行半徑為6 的PDE 靈敏度過濾拓撲優化實驗.其中，不同精度下懸臂梁和Michell 結構的優化結構、目標柔度值C、整體迭代次數I以及整體優化時間T的分布如圖4、圖5、表1、圖6、圖7所示.

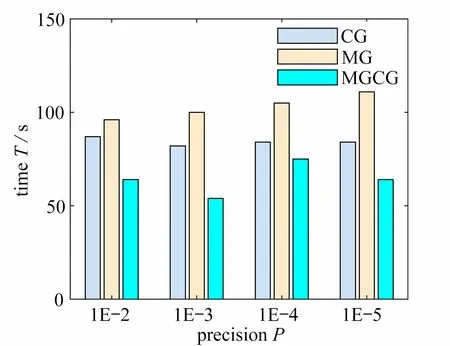
圖6 懸臂梁結構優化時間分布圖Fig.6 The optimized time distribution of the cantilever beam

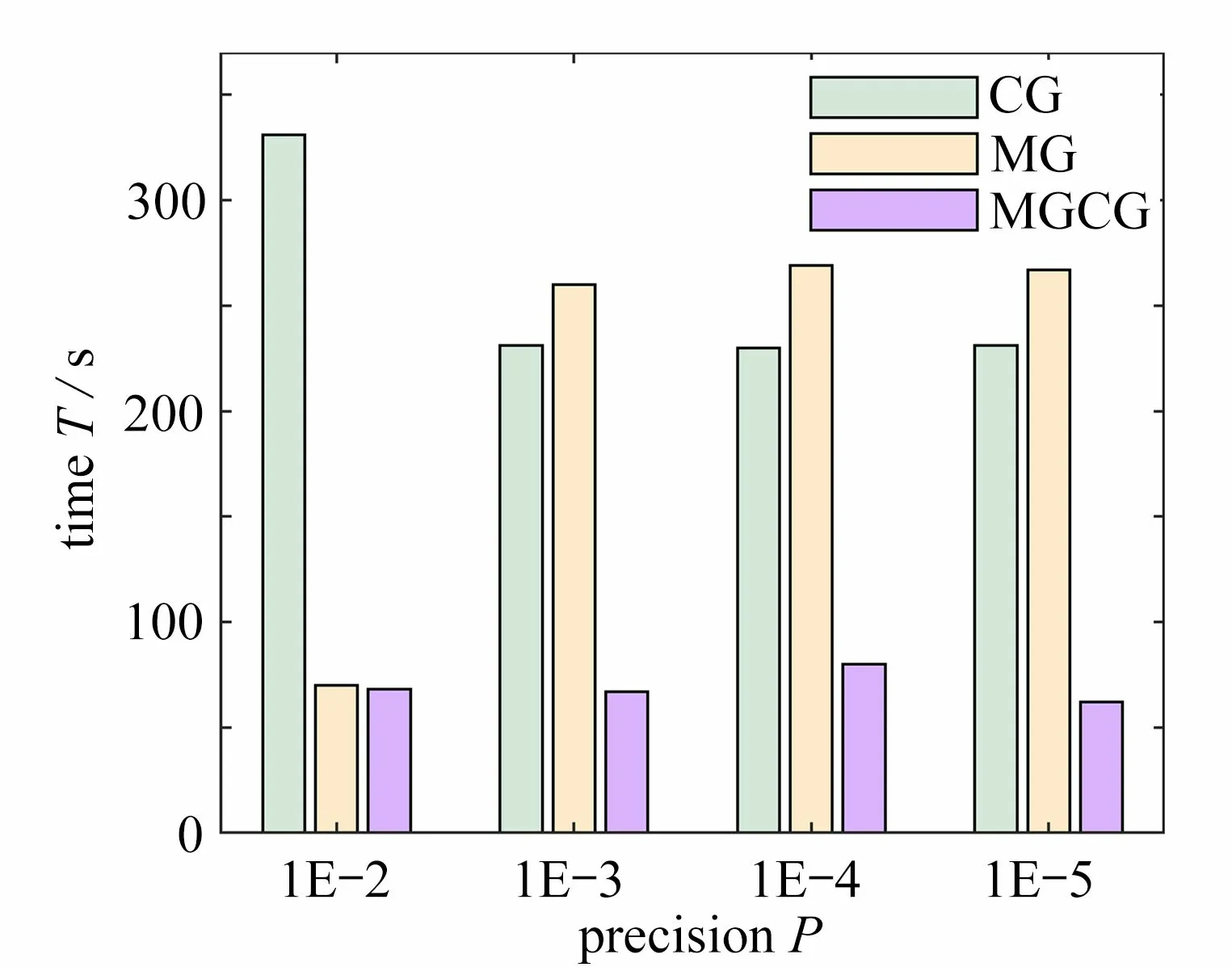
圖7 Michell 結構優化時間分布圖Fig.7 The optimized time distribution of the Michell structure

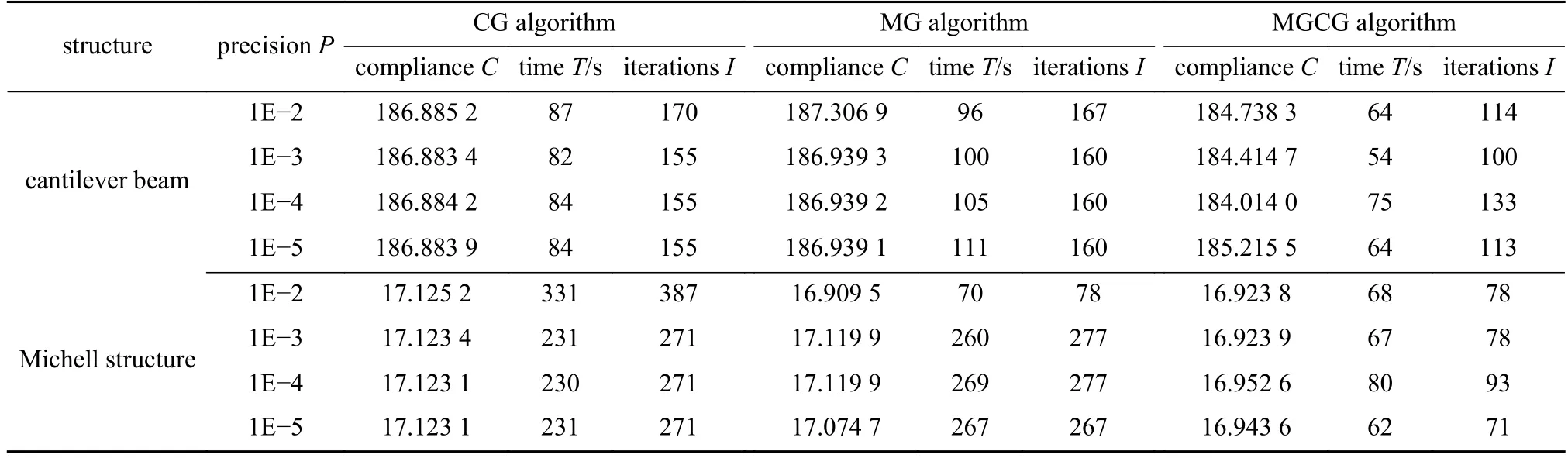
表1 兩種結構的拓撲優化迭代次數和柔度值Table 1 Total numbers of iterations and compliance for topology optimization of 2 structures

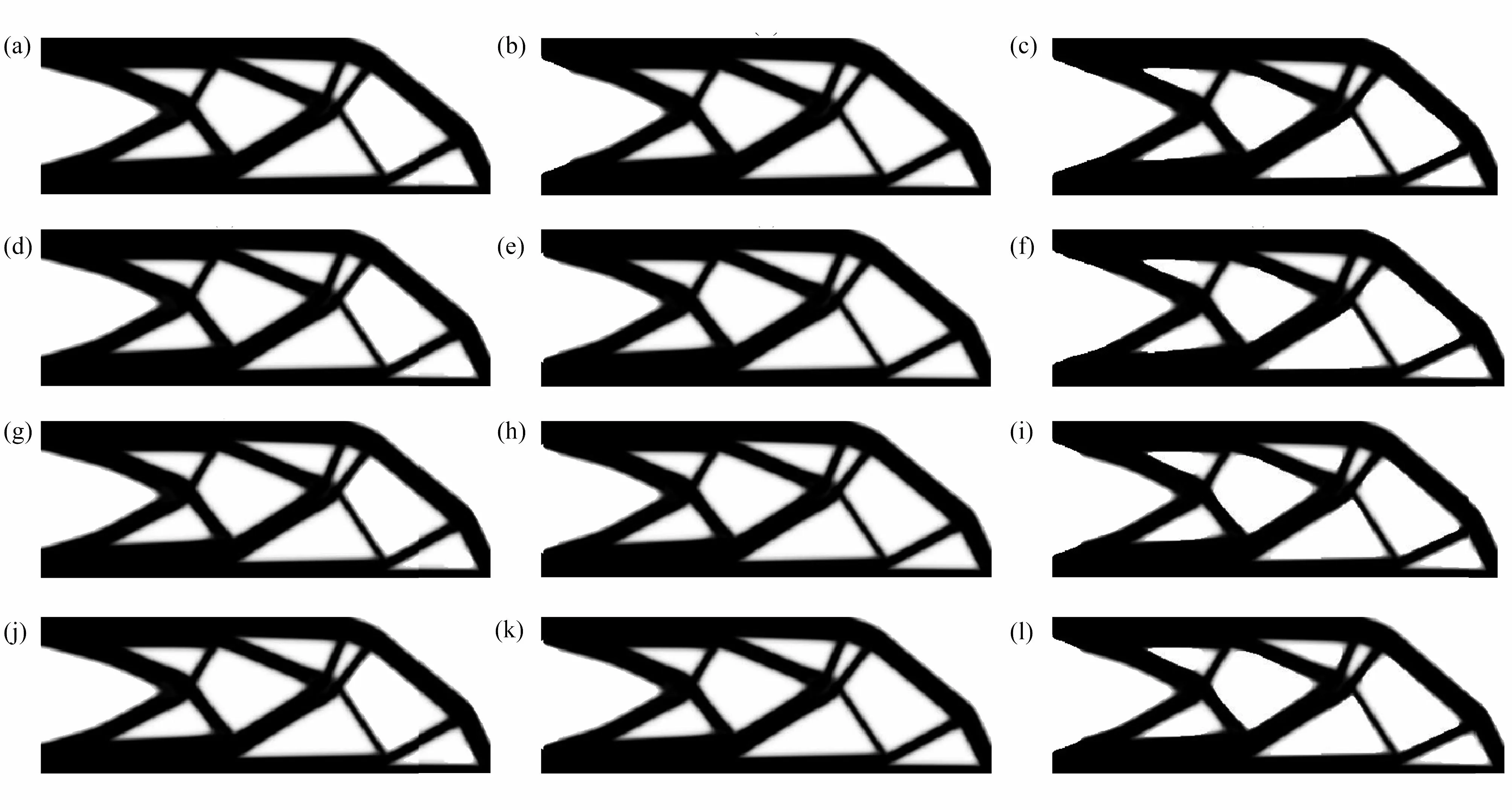
圖4 不同精度下CG、MG 和MGCG 算法的懸臂梁的優化結構：(a)P=1E?2 (CG)；(b)P=1E?2 (MG)；(c)P=1E?2 (MGCG)；(d)P=1E?3 (CG)；(e)P=1E?3(MG)；(f)P=1E?3 (MGCG)；(g)P=1E?4 (CG)；(h)P=1E?4 (MG)；(i)P=1E?4 (MGCG)；(j)P=1E?5 (CG)；(k)P=1E?5 (MG)；(l)P=1E?5 (MGCG)Fig.4 The optimized cantilever beams by CG,MG and MGCG algorithms with different degrees of precision:(a)P=1E?2 (CG);(b)P=1E?2 (MG);(c)P=1E?2 (MGCG);(d)P=1E?3 (CG);(e)P=1E?3 (MG);(f)P=1E?3 (MGCG);(g)P=1E?4 (CG);(h)P=1E?4 (MG);(i)P=1E?4 (MGCG);(j)P=1E?5 (CG);(k)P=1E?5 (MG);(l)P=1E?5 (MGCG)

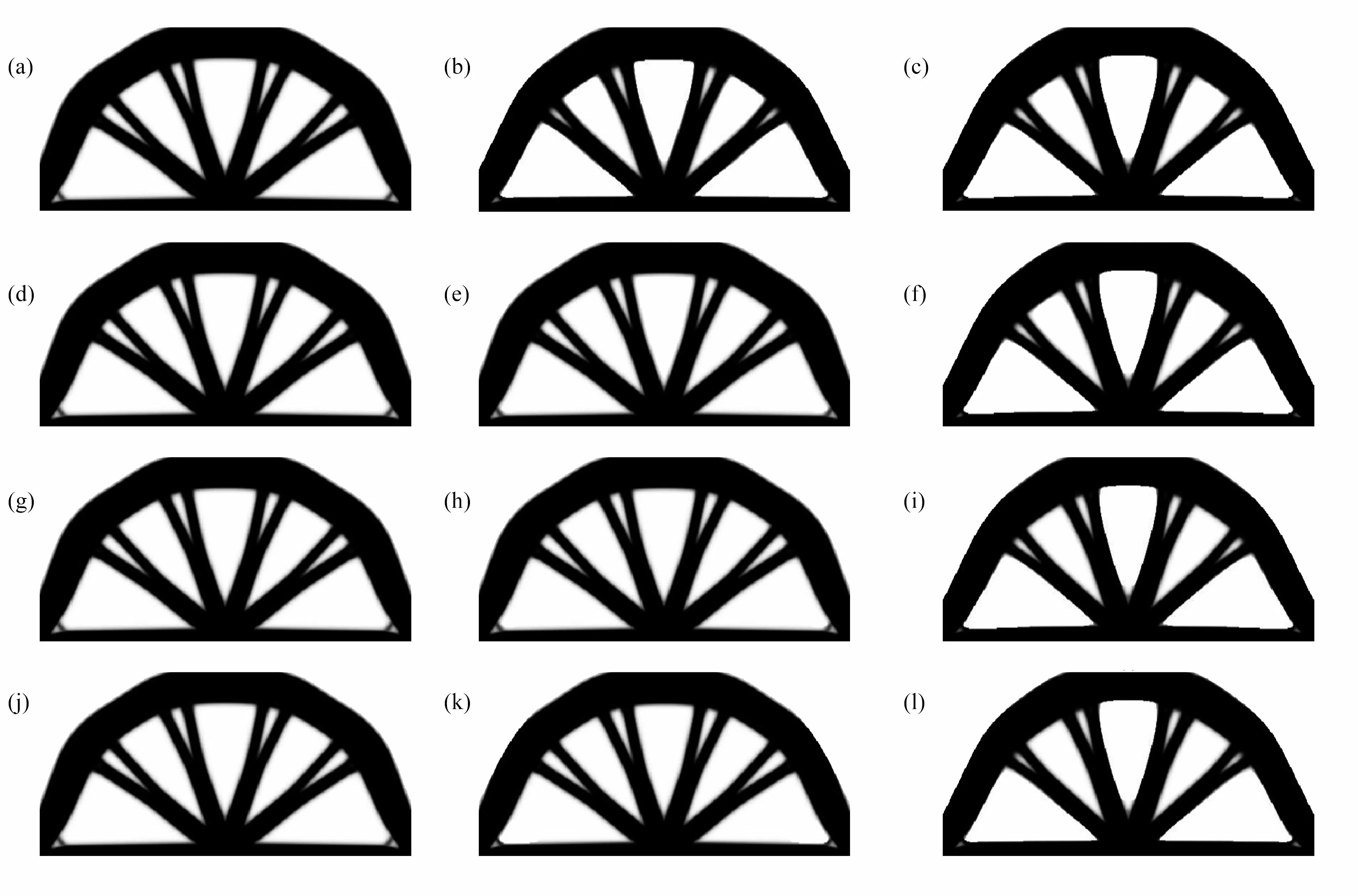
圖5 不同精度下CG、MG 和MGCG 算法的Michell 結構的優化結構：(a)P=1E?2 (CG)；(b)P=1E?2 (MG)；(c)P=1E?2 (MGCG)；(d)P=1E?3 (CG)；(e)P=1E?3(MG)；(f)P=1E?3 (MGCG)；(g)P=1E?4 (CG)；(h)P=1E?4 (MG)；(i)P=1E?4 (MGCG)；(j)P=1E?5 (CG)；(k)P=1E?5 (MG)；(l)P=1E?5 (MGCG)Fig.5 The optimized Michell structures by CG,MG and MGCG algorithms with different degrees of precision:(a)P=1E?2 (CG);(b)P=1E?2 (MG);(c)P=1E?2 (MGCG);(d)P=1E?3 (CG);(e)P=1E?3 (MG);(f)P=1E?3 (MGCG);(g)P=1E?4 (CG);(h)P=1E?4 (MG);(i)P=1E?4 (MGCG);(j)P=1E?5 (CG);(k)P=1E?5 (MG);(l)P=1E?5 (MGCG)

從圖4、圖5 和表1 可以看出，在過濾半徑為6 的PDE 靈敏度濾波器中使用不同精度的CG 算法、MG 算法和MGCG 算法得到的懸臂梁和Michell 結構的優化結構圖基本相同，并且目標函數值非常接近，至多相差1%，說明PDE 濾波器求解算法的精度對拓撲優化的結果影響不大.此外，在PDE 濾波器中使用MGCG 算法進行結構拓撲優化的迭代次數整體低于其他兩種算法.

從圖6 和圖7 可以看出，同一精度下，在PDE 濾波器中使用MGCG 算法進行結構拓撲優化的時間整體低于CG 算法和MGCG 算法，且隨著精度的增加，在PDE 濾波器中使用CG 算法進行結構拓撲優化的時間逐漸降低并趨于穩定，在PDE 濾波器中使用MG 算法進行結構拓撲優化的時間逐漸增加并趨于穩定.此外，在PDE 濾波器中采用MGCG 算法對懸臂梁和Michell 結構拓撲優化的時間分別比CG 算法少了11% ～ 34%和65% ～ 80%，比MG 算法少了29% ～ 46%，3%和77%.因此，從結構的整體優化效率看，MGCG 算法高于CG 算法和MG 算法.

3.2 過濾半徑的影響

依次取4 種不同的過濾半徑R(R=3，6，9，12),采用CG 算法、網格層數為5 的MG 算法以及MGCG 算法求解有限元分析Helmholtz 方程得到的代數方程，并對整個結構分別劃分為480×160和480×240個單元的懸臂梁和Michell 結構進行控制精度為1E–4 的PDE 靈敏度過濾的拓撲優化實驗.其中，不同過濾半徑下懸臂梁和Michell 結構的優化結構、目標柔度值C、整體迭代次數I以及整體優化時間T的分布分別如圖8、圖9、表2、圖10、圖11所示.

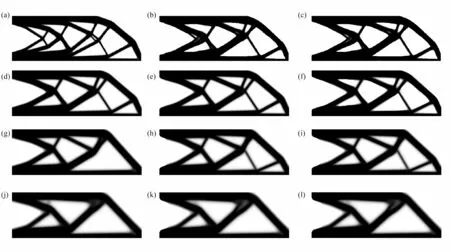
圖8 不同過濾半徑下CG、MG 和MGCG 算法的懸臂梁的優化結構：(a)R=3 (CG)；(b)R=3 (MG)；(c)R=3 (MGCG)；(d)R=6 (CG)；(e)R=6 (MG)；(f)R=6 (MGCG)；(g)R=9 (CG)；(h)R=9 (MG)；(i)R=9 (MGCG)；(j)R=12 (CG)；(k)R=12 (MG)；(l)R=12 (MGCG)Fig.8 The optimized cantilever beams by CG,MG and MGCG algorithms with different filter radius:(a)R=3 (CG);(b)R=3 (MG);(c)R=3 (MGCG);(d)R=6 (CG);(e)R=6 (MG);(f)R=6 (MGCG);(g)R=9 (CG);(h)R=9 (MG);(i)R=9 (MGCG);(j)R=12 (CG);(k)R=12 (MG);(l)R=12 (MGCG)

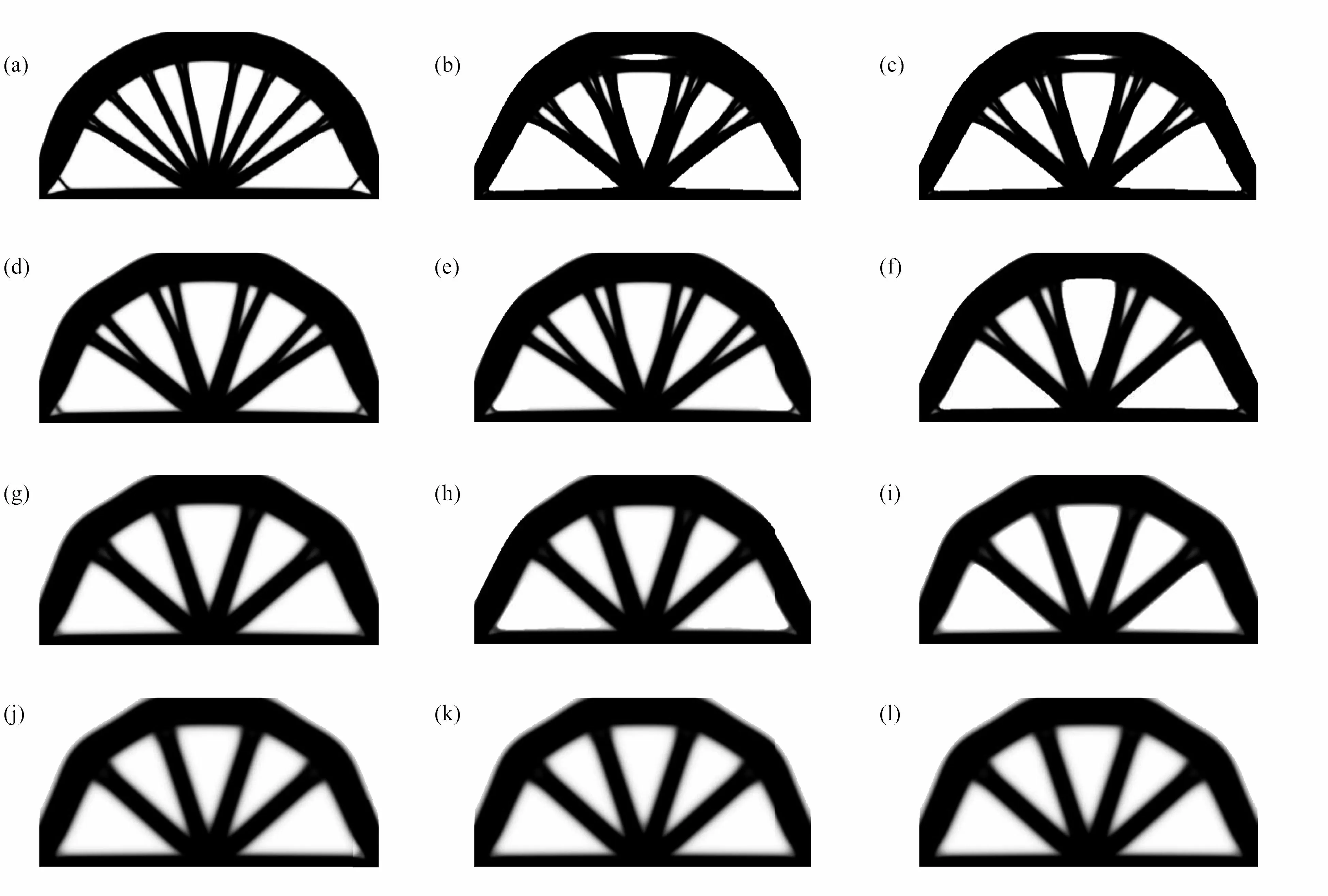
圖9 不同過濾半徑下CG、MG 和MGCG 算法的Michell 結構的優化結構：(a)R=3 (CG)；(b)R=3 (MG)；(c)R=3 (MGCG)；(d)R=6 (CG)；(e)R=6 (MG)；(f)R=6 (MGCG)；(g)R=9 (CG)；(h)R=9 (MG)；(i)R=9 (MGCG)；(j)R=12 (CG)；(k)R=12 (MG)；(l)R=12 (MGCG)Fig.9 The optimized Michell structures by CG,MG and MGCG algorithms with different filter radius:(a)R=3 (CG);(b)R=3 (MG);(c)R=3 (MGCG);(d)R=6 (CG);(e)R=6 (MG);(f)R=6 (MGCG);(g)R=9 (CG);(h)R=9 (MG);(i)R=9 (MGCG);(j)R=12 (CG);(k)R=12 (MG);(l)R=12 (MGCG)

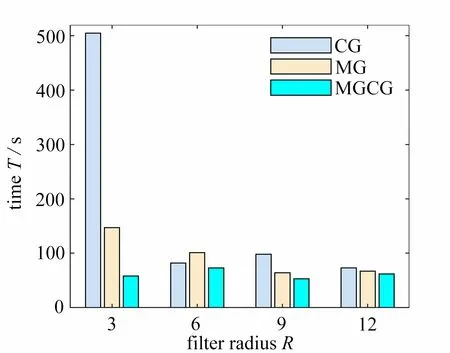
圖10 懸臂梁結構優化時間分布圖(不同過濾半徑)Fig.10 The optimized time distribution of the cantilever beam(different filter radius)

圖11 Michell 結構優化時間分布圖(不同過濾半徑)Fig.11 The optimized time distribution of the Michell structure(different filter radius)

從圖8、圖9 和表2 可以看出，在PDE 靈敏度濾波器中使用精度為1E–4 的CG 算法、MG 算法和MGCG 算法得到的懸臂梁和Michell 結構的優化結構圖、目標函數值的特征隨著過濾半徑的變化呈現類似的變化規律.隨著過濾半徑的增大，拓撲優化結構的清晰度越來越低，細支結構越來越少，說明該兩種算法對結構承力路徑的識別精度與過濾半徑間體現出負相關性，且柔度值越來越大.且從表2 可以看出，隨著過濾半徑的改變，在PDE 濾波器中使用MG 算法和MGCG 算法進行結構拓撲優化的迭代次數整體低于CG 算法.

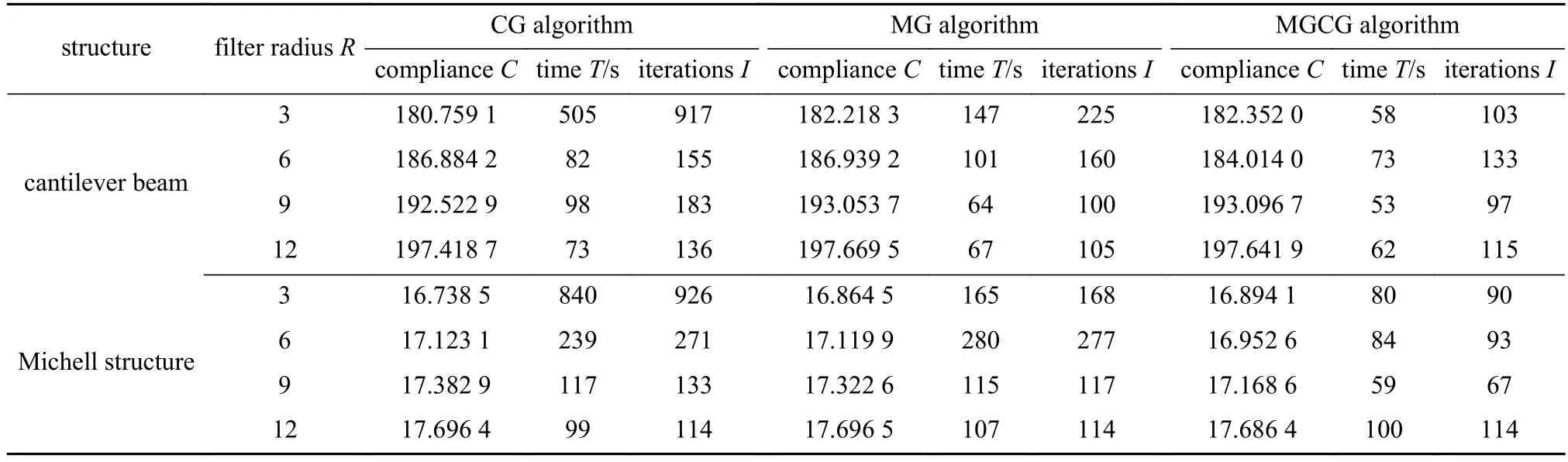
表2 兩種結構的拓撲優化迭代次數和柔度值(不同過濾半徑)Table 2 Total numbers of iterations and compliance for topology optimization of 2 structures (different filter radius)

從圖10 和圖11 可以看出，同一過濾半徑下，在PDE 濾波器中使用MG 算法和MGCG 算法進行結構拓撲優化的時間整體低于CG 算法，且隨著過濾半徑增大，MGCG 算法的優勢逐漸降低.此外，在PDE 濾波器中采用MGCG 算法對懸臂梁和Michell 結構拓撲優化的時間分別比CG 算法少了11%～89%和50%～91%，比MG 算法少了7%～61%，7%和70%.因此，從結構的整體優化效率看，MGCG 算法高于CG 算法和MG 算法.

3.3 網格數量的影響

分別對網格劃分為960×320，過濾半徑為12，層數為6；網格劃分為480×160，過濾半徑為6，層數為5；網格劃分為240×80，過濾半徑為3，層數為4 的懸臂梁和網格劃分為960×480，過濾半徑為12，層數為6；網格劃分為480×240，過濾半徑為6，層數為5；網格劃分為240×120，過濾半徑為3，層數為4 的Michell 結構進行控制精度為1E–4 的PDE 靈敏度過濾的拓撲優化實驗.其中，不同網格數量下懸臂梁和Michell 結構的優化結構、目標柔度值C、整體迭代次數I以及整體優化時間T的分布分別如圖12、圖13、表3、圖14、圖15所示.

從圖12、圖13 和表3 可以看出，在PDE 靈敏度濾波器中使用精度為1E–4 的CG 算法、MG 算法和MGCG 算法得到不同網格數量的懸臂梁和Michell 結構的優化結構基本相同，并且隨著網格數量增加，柔度值越來越大.可見PDE 濾波器求解算法對不同網格數量的優化結構影響不大，且可有效地消除網格依賴性和棋盤格現象.此外，在PDE 濾波器中使用MGCG 算法進行結構拓撲優化的迭代次數整體低于其他兩種算法.

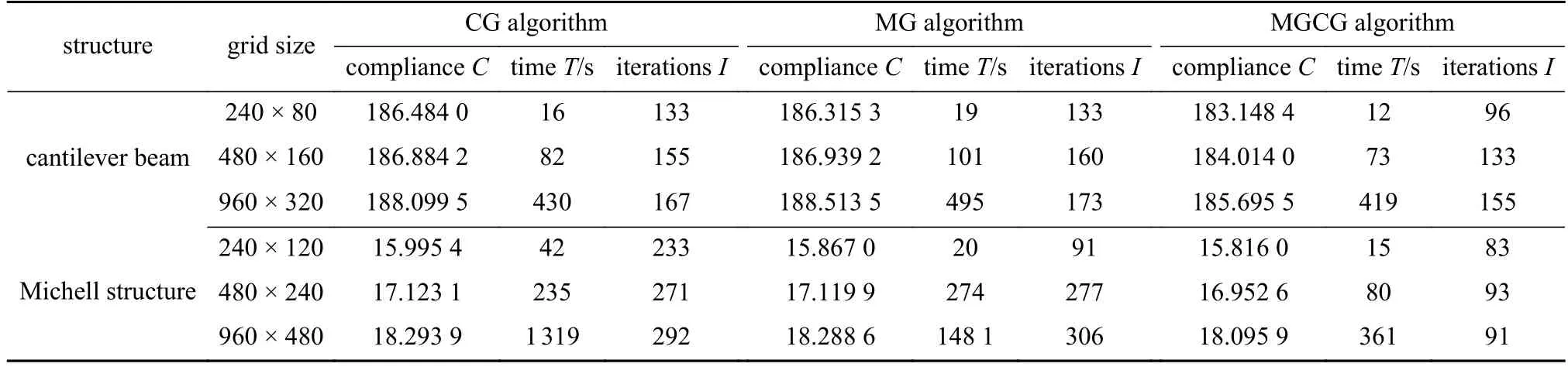
表3 兩種結構的拓撲優化迭代次數和柔度值(不同網格數量)Table 3 Total numbers of iterations and compliance for topology optimization of 2 structures (different grids)

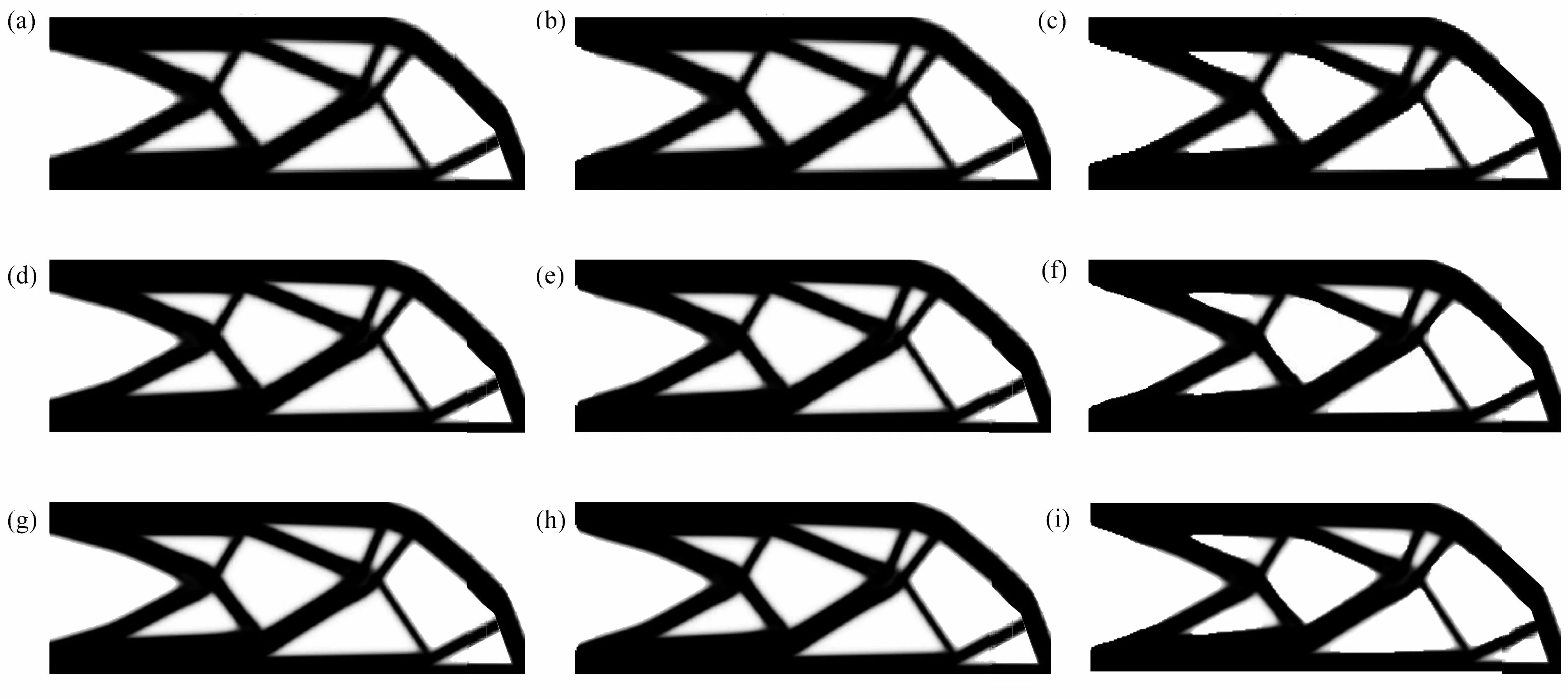
圖12 不同網格數量下CG、MG 和MGCG 算法的懸臂梁的優化結構：(a)網格為240 × 80 (CG)；(b)網格為240 × 80 (MG)；(c)網格為240 × 80 (MGCG)；(d)網格為480 × 160 (CG)；(e)網格為480 × 160 (MG)；(f)網格為480 × 160 (MGCG)；(g)網格為960 × 320 (CG)；(h)網格為960 × 320 (MG)；(i)網格為960 × 320 (MGCG)Fig.12 The optimized cantilever beams by CG,MG and MGCG algorithms with different grids:(a)grid 240 × 80 (CG);(b)grid 240 × 80 (MG);(c)grid 240 × 80 (MGCG);(d)grid 480 × 160 (CG);(e)grid 480 × 160 (MG);(f)grid 480 × 160 (MGCG);(g)grid 960 × 320 (CG);(h)grid 960 × 320 (MG);(i)grid 960 × 320 (MGCG)

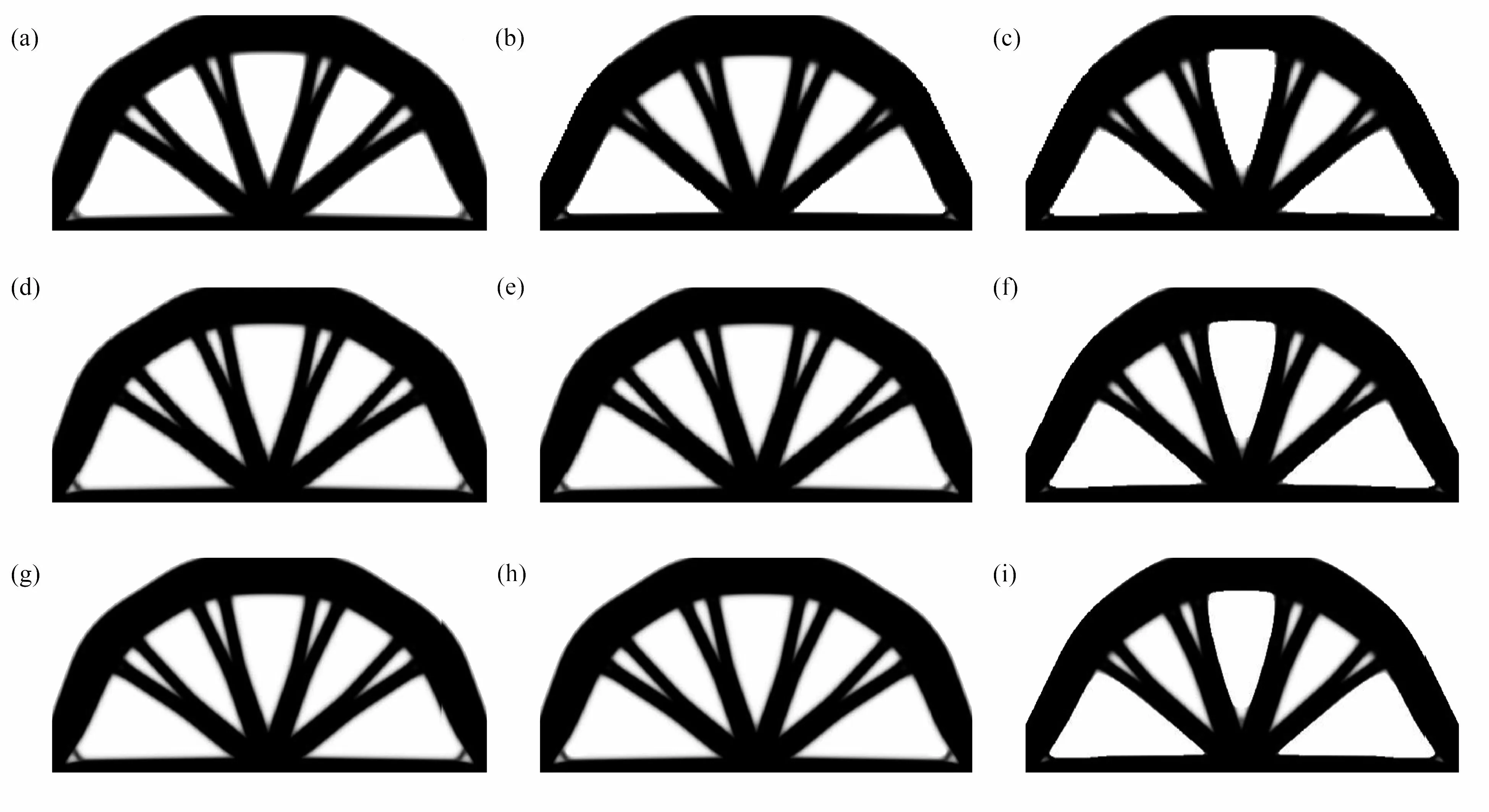
圖13 不同網格數量下CG、MG 和MGCG 算法的Michell 結構的優化結構：(a)網格為240 × 120 (CG)；(b)網格為240 × 120 (MG)；(c)網格為240 × 120 (MGCG)；(d)網格為480 × 240 (CG)；(e)網格為480 × 240 (MG)；(f)網格為480 × 240 (MGCG)；(g)網格為960 × 480 (CG)；(h)網格為960 × 480 (MG)；(i)網格為960 × 480 (MGCG)Fig.13 The optimized Michell structures by CG,MG and MGCG algorithms with different grids:(a)grid 240 × 120 (CG);(b)grid 240 × 120 (MG);(c)grid 240 × 120 (MGCG);(d)grid 480 × 240 (CG);(e)grid 480 × 240 (MG);(f)grid 480 × 240 (MGCG);(g)grid 960 × 480 (CG);(h)grid 960 × 480 (MG);(i)grid 960 × 480 (MGCG)

從圖14 和圖15 可以看出，同一網格數量下，在PDE 濾波器中使用MGCG 算法進行結構拓撲優化的時間整體低于CG 算法和MGCG 算法.特別地，在PDE 濾波器中采用MGCG 算法對懸臂梁和Michell 結構拓撲優化的時間分別比CG 算法少了3% ～ 25%和64% ～ 73%，比MG 算法少了15% ～ 37%，25%和76%.因此，從結構的整體優化效率看，MGCG 算法高于CG 算法和MG 算法.

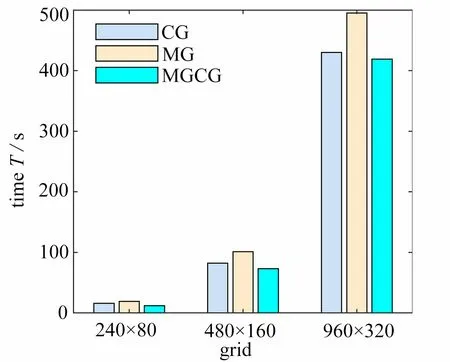
圖14 懸臂梁結構優化時間分布圖(不同網格數量)Fig.14 The optimized time distribution of the cantilever beam(different grids)

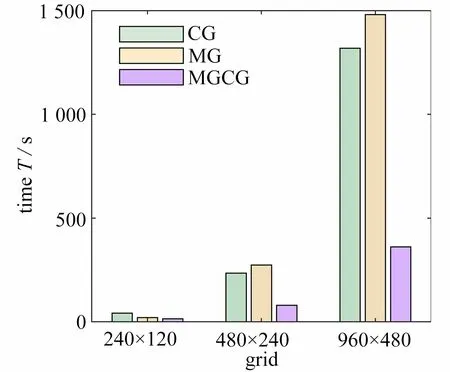
圖15 Michell 結構優化時間分布圖(不同網格數量)Fig.15 The optimized time distribution of the Michell structure(different grids)

4 結論

本文在PDE 靈敏度濾波器中引入了CG 算法、MG 算法和MGCG 算法，對懸臂梁和Michell 結構進行拓撲優化，并比較了算法精度、過濾半徑和網格數量對優化結果和優化效率的影響.實驗結果表明：

1）不同精度的三種算法得到的優化結構、目標函數值基本相同.隨著精度的提升，MG 算法的結構優化時間不斷增加，CG 算法總體趨于穩定，MGCG 算法有微小的波動，且MGCG 算法結構優化時間整體少于其他兩種算法.

2）隨著過濾半徑的增大，CG 算法和MG 算法的結構優化時間大幅減少，整體呈下降趨勢，MGCG 算法有微小的波動，但優化時間整體少于其他兩種算法，且過濾半徑越小，優勢越明顯.

3）不同網格數量的三種算法得到的優化結構、目標函數值基本相同.隨著網格數量的增加，三種算法的結構優化時間和迭代次數整體呈上升趨勢，且隨著網格數量的增加，MGCG 算法的優勢越明顯.

因此，從結構的整體優化效率看，MGCG 算法優于CG 算法和MG 算法.