基于Transformer模型的電力負荷預測

王園浩 朱月堯 查易藝

（1.南京理工大學自動化學院，江蘇南京 210094；2.國網江蘇省電力有限公司淮安供電分公司，江蘇淮安 223022；3.國網江蘇省電力有限公司信息通信分公司，江蘇南京 210024）

0 引言

電力系統的主要任務是為用戶提供標準且穩定的電能，以滿足生活中各類負荷的用電需求，由于目前難以實現電能的大量存儲，故為使電力系統穩定運行，需要實時動態地平衡發電量與負荷變化[1]。為保證電網經濟且穩定運行，應按需發電并合理分配負荷，其關鍵點在于如何對電力系統負荷進行精準預測。

電力系統負荷預測是電力系統規劃的重要組成部分，也是電力系統經濟運行的基礎[2]。細化到民用領域，居民用電量本質上是一系列的時序數據，故可用時序預測問題予以建模，它能從已知的歷史用電需求出發來預測未來的用電需求。傳統的電力系統負荷預測常采用基于時間序列的方法，例如文獻[3]從負荷影響因素的復雜性和隨機性考慮，以電力系統負荷為因變量，經濟、人口、季節為自變量構建回歸方程，利用多元線性回歸模型進行預測；文獻[4]利用灰色模型（Grey Model，GM）擬合電力負荷的增長趨勢，再利用馬爾可夫鏈（Markov Chain，MC）修正預測結果；文獻[5]利用粒子群算法（Particle Swarm Optimization，PSO）對灰色模型的參數進行適當優化，并使用傅里葉變換對預測誤差進行修正，但灰色預測法需要負荷序列連續平滑且符合指數變化規律，該方法雖聯合了尋優算法，但仍未擺脫灰色模型的框架。

電力系統負荷最大的特點在于非線性，以上方法雖然計算速度快，但是無法解決序列非線性的問題，故精度欠佳，難以在電力系統規劃與電網調度中發揮重要作用。為解決電力負荷序列非線性強從而導致難以準確預測的問題，一批機器學習算法開始涌現：支持向量機（Support Vector Machine，SVM）對高維度的非線性問題有較好的處理能力，文獻[6]使用SVM對某區域一天內的短期電力負荷進行預測，一定程度上解決了歷史數據有限且系統非線性的問題；文獻[7-8]等采用了隨機森林（Random Forest，RF）算法，但該方法在噪聲較大的數據上會出現較為明顯的過擬合問題。近年來火熱的人工智能算法在傳統機器學習算法的基礎上更進一步提高了對非線性數據的擬合能力，理論上神經網絡模型可以擬合任意非線性函數，其中基于反向傳播（Back Propagation，BP）[9-10]的神經網絡模型被最早應用于電力系統負荷預測領域，并在短期預測領域取得了較為成熟的結果。

但電力實際調度時，不僅要進行短期預測，往往還需要進行中長期預測，處理長時序數據，這要求算法必須具備記憶能力，以從海量數據中提取有效的時間特征，保證算法預測精度，傳統BP算法無法滿足要求，被以長短時記憶網絡（Long Short-Term Memory，LSTM）為首的循環神經網絡（Recurrent Neural Network，RNN）算法取代，其緩解了傳統RNN 存在的梯度爆炸及梯度消失問題，且具備記憶能力。文獻[11-12]采用LSTM 算法及其變體取得了優于傳統時間序列方法與人工智能算法的預測精度；文獻[13]利用LSTM 模型對中國股市中的一些銀行股股價進行預測，其預測結果在200個時間步內較好地捕捉了股價的漲跌趨勢。LSTM 并非完美，受其原理所限，LSTM 網絡無法進行并行計算，在工程實踐中極大地浪費了計算資源，并且該網絡模型記憶能力有限，對于數據中的長期依賴特征無法很好地提取，在處理中長期預測任務時，其性能表現仍有進一步的提升空間。Transformer克服了傳統LSTM 存在的一些問題，可以在時序中建立較好的長時依賴性。文獻[14]利用Transformer模型對網購平臺多種商品的價格與銷量進行預測，很好地體現了Transformer在處理長時序信息時的能力；文獻[15]將Transformer模型應用于行人軌跡預測，并取得了比LSTM 更好的預測結果。

在本文中，受Transformer模型優勢的啟發，將Transformer模型從機器翻譯領域引入電力系統負荷預測領域，構建基于Transformer的用電負荷預測模型，并對某區域內20戶用戶一年內的用電負荷以小時為粒度構建數據集，以訓練模型并驗證預測精度。實驗結果表明，Transformer模型取得了優秀的預測精度，較好地預測了用電負荷可能出現的波動，且無時滯效應。

1 Transformer電力負荷預測模型

Transformer是一種以編碼器-解碼器為結構的神經網絡，核心是自注意力機制，在2017年由Vaswani等人[16]首次提出，并在需要處理海量長文本信息的機器翻譯領域取得了極大的成功。該領域常以整本小說作為訓練數據，要準確翻譯必須建立相當跨度的長期依賴關系以理解文本中包含的大量上下文信息。Transformer很好地解決了這個問題，同時該網絡模型可以進行并行計算，且具備強于LSTM 的長期記憶能力。此外，在序列輸入模型進行訓練的過程中，不同時間步數據之間的距離均為O（1），從而徹底克服了RNN 模型梯度爆炸和梯度消失的問題，大大提升了模型訓練成功的概率及計算效率。

Transformer整體結構如圖1所示，從組織結構的角度來看，該模型主要可以分為三個部分：嵌入部分、編碼器-解碼器部分與邏輯回歸部分。

圖1 Transformer模型網絡結構示意圖

1.1 嵌入部分

電力負荷數據一大特點是序列性，RNN 網絡通過對輸入序列進行迭代操作的方式將序列中每個時間步的位置信息賦予網絡模型，這也直接導致了RNN網絡無法并行計算，必須串行迭代，而Transformer神經網絡打破了該桎梏，但也面臨一個問題，即如何將每個時間步的位置信息準確提供給模型，讓模型明白輸入序列的順序關系。為解決該問題，Transformer神經網絡首先對輸入序列中的每個數據進行詞嵌入（Word Embedding，WE）操作，詞嵌入將原本一維的數據升維成二維矩陣，將輸入序列中的每個數值均映射為512維的特征行向量。之后Transformer神經網絡通過正余弦函數對輸入序列進行編碼并生成固定的絕對位置表示，即位置編碼（Positional Encoding，PE），再將其與之前完成詞嵌入的序列對位相加。其位置編碼公式如下：

式中：pos為某時間步數據所在輸入序列中的位置索引；dmodel為輸入序列詞嵌入的維度；i為向量的某一維度。

1.2 編碼器-解碼器部分

1.2.1 自注意力機制

編碼器-解碼器的核心是自注意力機制。自注意力機制將輸入序列映射為問題-鍵-值（query-key-value）并計算一個問題與所有鍵的點積以得到權重，從而學習到每個數據與序列中所有其他數據之間的相對重要性。其計算過程如下：

式中：Q代表問題；K代表鍵；V代表值，并以詞嵌入維度dmodel作為縮放因子，可以使梯度在訓練過程中更加穩定。

Transformer神經網絡通過自注意力機制，使得模型更關注輸入序列數據之間的內在聯系，降低了模型發生反常預測的概率，從而為電力負荷預測任務提供了偶然性過濾能力，使網絡模型更加穩定與魯棒。

1.2.2 多頭自注意力

在工程實際中，Transformer神經網絡在自注意力機制的基礎上升級為多頭注意力機制，該機制將單個注意力拆分成8個，即將式（2）中的一組Q、K、V拆分成8組等大小的Qi、Ki、Vi，i=1，2，…，8，并在這些組內分別進行注意力操作，最后將每個小組的輸出重新拼接為原始大小，作為多頭注意力層的輸出。多頭注意力層可以形成多個子空間，讓模型去關注不同子空間內的信息，最后將各個方面的信息綜合起來，有助于網絡捕捉到更豐富的特征信息，提升模型預測精度。

1.2.3 編碼器整體結構

Transformer神經網絡編碼器的結構由圖1左側部分組成，設輸入序列為用戶耗電量X，則編碼器計算過程可表示為如下四步：

（1）對輸入序列進行詞嵌入與位置編碼：

（2）自注意力機制先計算問題矩陣Q、鍵矩陣K、值矩陣V：

式中：WQ、WK、WV為隨著電力負荷預測模型訓練而不停學習更新的權值矩陣，經過嵌入后的輸入序列與之點乘、進行線性變換而得到矩陣Q、K、V。

之后按公式（2）計算自注意力得分：

（3）殘差連接與層歸一化：

（4）以ReLU 為激活函數的全連接線性映射，得到編碼器向隱藏層的輸入：

1.2.4 帶遮擋的自注意力

解碼器的整體計算流程與編碼器大致相同。傳統序列到序列模型中的解碼器常使用RNN 模型，該網絡模型由時間驅動，在訓練中，模型只能看到當前t時刻的輸入，無論如何也看不到未來時刻的值。而基于自注意力機制的解碼器在訓練時，整個序列都暴露在解碼器中，會導致真值提前泄露，故需要對輸入解碼器的序列進行遮擋（Mask）操作，具體操作如圖2所示。

圖2（a）為自注意力矩陣，考慮到負無窮經過Softmax函數映射后為0，故選用下三角全零、上三角負無窮的矩陣作為遮擋矩陣，如圖2（b）所示。將自注意力矩陣與遮擋矩陣逐元素相加即可得到帶遮擋的自注意力得分。

圖2 輸入遮擋

1.3 邏輯回歸部分

邏輯回歸部分如圖1中右側灰色部分所示，由一個線性變換與Softmax映射組成，其作用是將解碼器的輸出回歸到輸出向量空間中并重新映射為下一時刻用電負荷的預測概率。

2 基于Transformer的電力負荷預測

2.1 用電負荷數據預處理

在用電負荷預測問題中，每戶用戶的用電量都存在一些潛在特征，這些特征的量綱與數值量級上均存在差異，如果直接將用戶原始的用電數據提供給預測模型進行訓練，將容易導致模型難以收斂而達不到理想的訓練效果。為此，本研究引入標準化（Normalization）以克服以上問題，它將不同的特征規整到統一尺度上，使其具有可比性。其計算方法如下：

式中：X為用戶原始用電負荷樣本；X′為標準化后的用電負荷樣本；μ為全部樣本的樣本均值；σ為全部樣本的標準差。

經過標準化后，所有樣本的均值為0，標準差為1，且可以提升模型在訓練時梯度下降的速度。

2.2 用電負荷預測流程

用電負荷預測的重點是對用戶歷史耗電數據的長時依賴特征進行學習并擬合其背后的非線性曲線，Transformer神經網絡具有可以擬合強非線性曲線的優秀性質，故本文采用Transformer神經網絡對用戶用電負荷進行預測，其過程如下：

步驟1，收集某區域20戶用戶以每小時為粒度的歷史用電數據。

步驟2，標準化數據。

步驟3，對標準化后的用戶歷史用電數據建立時序數據集，并將其劃分為訓練集、驗證集和測試集。

步驟4，構建Transformer神經網絡預測模型，設置參數與超參數后使用訓練集訓練模型，使用驗證集驗證模型訓練效果。

步驟5，取測試集中一定幀數的歷史用電數據樣本輸入Transformer神經網絡預測模型，由模型預測后續一定時長的用戶用電負荷。

3 實驗結果及結論分析

3.1 實驗設定

為充分且有效地訓練模型，本文使用某地區20戶居民2012年1月1日00：00至2012年12月31日24：00以每小時為粒度的用電負荷構建數據集，共計8 784 h、175 680個數據點。進一步地，將其中85% 的數據作為訓練集，由于數據量較為充足，所以采用其中的5% 作為驗證集便能很好地檢驗模型訓練效果，而最后的10% 則作為測試集用于測試模型訓練完成后的最終預測精度。在驗證模型預測精度時，選用均方誤差（Mean Square Error，MSE）與平均絕對誤差（Mean Absolute Error，MAE）度量，設一共預測mh的用電負荷，yi為實際用電負荷值，為模型預測用電負荷值，則MSE與MAE的計算方式如下：

在結構選擇時，Transformer的電力負荷預測模型共使用6層編碼器、3層解碼器；輸入數據的詞嵌入維度為512維；在多頭注意力層中使用8個頭，以將特征投影到8個不同的特征空間中。在訓練模型時，初始學習率為0.001，且每輪訓練之后先將學習率乘以0.8再開始新一輪訓練，這樣做既可以讓模型快速收斂，又可以盡量去逼近損失函數的全局最優值。本文損失函數采用的是最小均方誤差（MSE），將損失從解碼器的輸出傳播回整個模型。

3.2 實驗結果

為充分探究Transformer預測模型對用電負荷進行預測的潛力，使用該模型對20戶用戶用電負荷進行24、48、168、512 h四種不同時長的預測，每種時長預測10次，其以MSE與MAE度量的預測精度展示如圖3所示。

由圖3可見，Transformer模型對用電負荷進行預測時精度相當高且表現穩定，在時序預測領域MSE與MAE低于1則視為可用，本文所研究模型精度高于可用精度閾值的5～7倍。此外，該模型的預測誤差雖然隨預測時長的增加而上升，但趨勢非常緩慢：預測24 h最小MSE與MAE分別為0.121 82與0.236 51，預測512 h最大MSE與MAE分別為0.176 31與0.292 46，以24 h預測結果為基準可知，預測時長增加至21.33倍時，MSE預測誤差僅增長44.73%，MAE預測誤差僅增長23.66% 。由此可見，Transformer模型可以充分捕捉用戶用電負荷中的長期依賴特征并由此進行精準的預測，在預測時長倍增的同時能夠有效控制住誤差的增長，具備非常強的長期預報能力，方便電網工作人員進行長期規劃，提前為可能出現的用電高峰或低谷做準備，以保證電網的經濟運行。

圖4為進行標準化后的預測結果，選用標準化后的結果進行展示可以消除量綱對預測結果的影響，更直觀地展示模型的預測精度。由圖4可知，雖然預測負荷的精度在波動的峰值處可能有所欠缺，但Transformer模型無論預測時間長短，均可較好地預測用電負荷波動的趨勢，且沒有明顯的時滯效應。

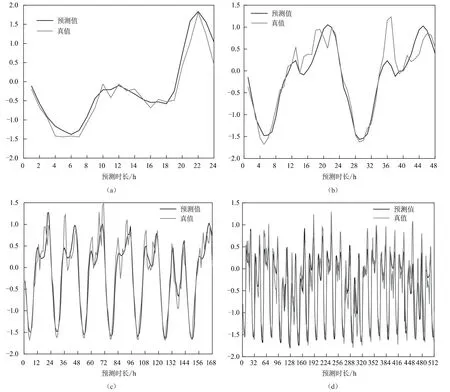
圖4 不同長度歸一化后預測結果

4 結語

數字化技術在電網企業生產經營等多個專業領域得到了推廣運用，運用人工智能方法，對電力系統負荷進行準確的預測，全面挖掘數據價值，對于電網穩定且經濟運行具有重要意義。鑒于傳統神經網絡預測方法受限于RNN 結構的劣勢，無法進行長期精準預測，本文提出了基于Transformer模型的用電負荷預測方法，并通過仿真實驗證明了該方法在預測長期用電負荷時精度高，可以較好地預測用電負荷可能出現的波動且無時滯效應。后續工作可以考慮加入先驗的專家知識，如季節、氣候等因素，以進一步提高模型的預測精度，優化模型在波動峰值處的表現。