爆炸波在復合鋼板襯砌結構中的傳播規律研究★

趙 越，劉 曉,李慶洲，趙明凱，宋 城

(1.蘭陵縣公共住房經營有限公司，山東 蘭陵 277700；2.民航機場智能建造與工業化工程技術研究中心，天津 300456；3.民航機場建設工程有限公司，天津 300456；4.山東科技大學土木工程與建筑學院，山東 青島 266590)

隨著我國的城市化進程不斷加快，交通擁堵問題日益顯著，地鐵作為一種便捷的交通方式，憑借其節約地面空間、噪聲小、污染小的優點在全國范圍內得到了大力推廣。地鐵隧道的發展加快了出行速度，有效地滿足了城市交通需求，但也極易成為恐怖分子實行爆炸襲擊活動的重點目標，存在一定的安全隱患。其中，復合鋼板可以作為一種襯砌防護結構，能夠吸收爆炸沖擊波帶來的能量，并且具有較高的抗剪強度，在地鐵區間隧道的抗爆防護方面具有很高的適用性。因此，研究爆炸沖擊波在復合鋼板襯砌結構中的傳播規律，在減少恐怖爆炸活動造成的財產損失和人員傷亡等方面有著重要的研究價值[1-3]。

要對地鐵隧道實行合理有效的防護措施，了解爆炸沖擊波[4]在隧道中的傳播規律是保證地鐵隧道安全運行的關鍵。與地上空間相比，地鐵隧道區間是一個相對的“封閉系統”，炸藥在地鐵隧道區間中爆炸產生的空氣沖擊波會在封閉空間內部不斷地傳播和反射，其傳播規律相比于傳統空氣沖擊波而言更加復雜[5-6]。目前，有關爆炸荷載在地鐵隧道中的沖擊反應研究主要可以分為試驗方法和數值方法。張玉磊等[7]使用不同藥量的TNT開展了靜爆實驗，研究了不同裝藥量級TNT產生的爆炸沖擊波在空氣中的傳播規律。爆炸試驗非常昂貴，試驗的可控性差，并且具有一定的風險性。因此，為彌補試驗方法的不足，數值模擬方法得到了快速發展。

SMITH等[8]分別采用模型試驗和數值模擬的方法研究了地下封閉空間內部產生的爆炸沖擊波對襯砌結構的影響規律。孔德森等[9]基于實際的工程地質條件，采用流固耦合算法研究了爆炸沖擊波對地鐵區間隧道的沖擊反應。李世強等[10]采用有限元軟件AUTODYN研究了爆炸沖擊波在某地鐵車站內的傳播規律和衰減規律，并得出了沖擊波的殺傷范圍。曲樹盛等[11]采用Euler方法研究了爆炸沖擊波在隧道區間的傳播過程，得出了避免人員傷亡的安全距離，并分析了結構高度和出口距爆炸源的距離對沖擊波傳播的影響。GIANNOPOULOS等[12]采用激光掃描方法獲取地鐵車站及車廂的幾何數據，使用EURO-PLEXUS程序的風險分析模塊研究了不同裝藥量的TNT在地鐵隧道區間爆炸后帶來的損害。以上研究主要集中在爆炸沖擊波在未設防護的地鐵區間隧道的傳播規律及殺傷范圍。然而，目前有關爆炸沖擊波在已設有復合材料防護的地鐵區間隧道內的傳播規律研究還不多見，研究成果也不夠全面。

鑒于上述研究成果，基于流體動力學和爆炸學中的知識，本文提出了一種使用復合鋼板作為襯砌結構的地鐵防爆方法，建立了空氣-炸藥-復合鋼板襯砌結構-周圍土體的爆炸沖擊模型。在地鐵隧道區間使用復合鋼板作為防護結構的條件下，研究了不同TNT炸藥當量下爆炸沖擊波的反射疊加效應和衰減規律，為地鐵的抗爆防護設計提供參考依據。

1 數值模型的建立

1.1 復合鋼板襯砌防護結構

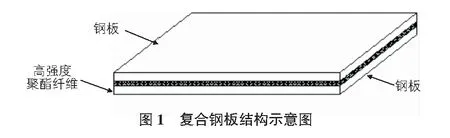
復合鋼板兼備金屬材料和高分子材料的特性，被視為代替金屬板的理想環保材料，具有防振和防噪聲的優良性能。基于復合鋼板的以上優良特性，將其應用于地鐵隧道的防護領域[13]。復合鋼板襯砌結構是由高強度聚酯纖維和兩層鋼板組成，其厚度比例為2∶1∶2，其中高強度聚酯纖維在兩層鋼板之間，采用焊接法制成。將其作為隧道的抗爆結構，具有良好的延展性和硬度，滿足防護材料所需要的性能指標。復合鋼板的結構特征見圖1。

由于爆炸沖擊波在地鐵隧道區間的傳播過程中呈現出非線性特征，使用雙線性彈塑性本構模型[14]來描述復合鋼板襯砌結構，使用Cowper-Symonds模型來描述復合鋼板材料的應變率。因此，防護結構的動態屈服強度可以表達為：

(1)

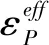
表1 復合鋼板襯砌結構的參數值

1.2 防護結構模型的建立

本文以南京市某地鐵隧道工程為依托，使用動力學分析軟件LS-DYNA建立復合鋼板襯砌防護結構的數值模型。其數值模型結構簡圖如圖2所示。

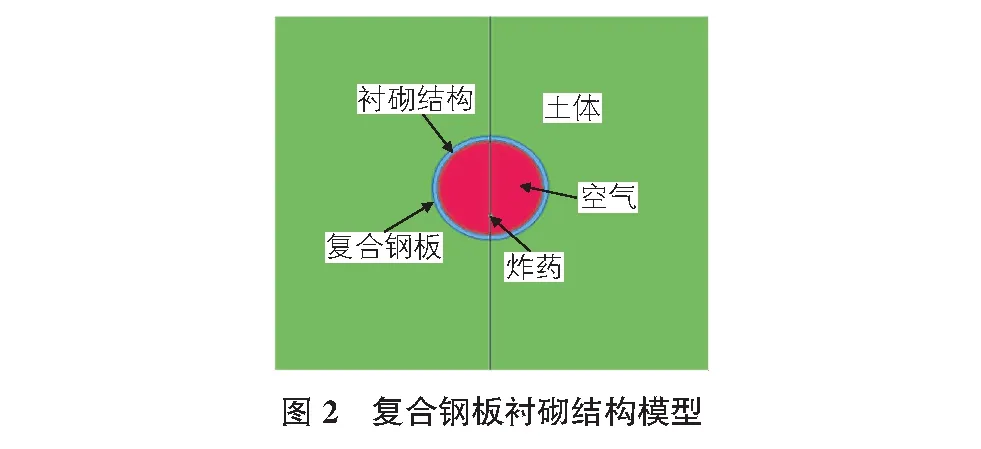
研究對象為圓筒形盾構隧道，埋深為15 m，外徑為6.0 m，內徑為5.4 m，復合鋼板厚度為0.1 m，襯砌厚度為0.3 m。由于防護結構模型具有對稱性，因此在建模計算過程中使用1/2模型。同時為減少邊界效應，建立尺度為36×36×15的立方體結構作為整體的爆炸沖擊模型，分別研究在10 kg TNT與30 kg TNT炸藥當量下，爆炸源距離防護結構底部1.1 m處時產生的沖擊效應。

1.3 炸藥燃燒模型與參數

由于爆炸是瞬間發生的，因此可以忽略爆炸產生的沖擊波在炸藥和介質交界處之間的傳播時間，只研究爆炸沖擊波的外部傳播規律[15]。炸藥的爆炸參數列于表2。

表2 爆炸參數

TNT炸藥產生的爆炸沖擊效應可以使用JWL狀態方程進行描述。爆炸產生的壓力可以由單位體積的初始內能和相對體積來表達：

(2)

其中，P為壓力；V為相對體積；E0為單位體積的初始內能；A，B，R1，R2，ω均為材料系數。基于LS-DYNA程序提供的“*EOS-JWL”關鍵字描述狀態方程，將使用的具體參數值列于表3。

表3 JWL狀態方程參數

整體結構中土體部分使用MAT-SOIL-AND-FOAM模型來描述。屈服函數f可以表達為：

f=J2-(a0+a1p+a2p2)

(3)

土體的變形特征使用Drucker-Prager屈服準則來描述。因此，土體的內摩擦角φ和土的黏聚力c可以表示為：

(4)

(5)

2 數值模型的計算結果分析

2.1 隧道結構受到爆炸沖擊的應力分布

由于爆炸產生的沖擊波是在半封閉的地鐵區間隧道內進行傳播，防護結構的動力響應變得更加復雜。因此，只研究模型內部空氣的相關力學特性。同時，爆炸產生的沖擊波作用時間短、頻率高，從零荷載到最大值荷載只需要幾毫秒。此外，防護結構在沖擊波作用下產生的應力應變行為與沖擊波的作用速率呈正相關。因此，為了更有針對性地研究爆炸荷載峰值的破壞作用并節約計算時間，數值模型的爆炸時間取50 ms。10 kg TNT炸藥作用下與30 kg TNT炸藥作用下襯砌防護結構各時間點的應力變化特征如圖3所示。

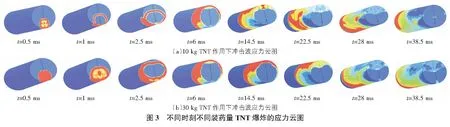
由圖3可以看出，炸藥爆炸產生的沖擊波會以球形波陣的形式向外傳播，30 kg TNT作用下產生的沖擊波能量更大，影響范圍更廣。爆炸點距離隧道底部僅有1.1 m，因此，爆炸沖擊波會率先作用于襯砌底部。隨著沖擊壓力增大，爆炸作用下的反射波繼續向更遠的范圍內傳播，隨著距離的增加，爆炸產生的沖擊波壓強逐漸降低。同時，沖擊波會在地鐵區間隧道內部產生多次反射，這種反射疊加作用使隧道的爆源截面上出現多次應力峰值，并減緩了沖擊波強度的衰弱作用，沖擊傳播規律更為復雜。此外，爆炸發生初期，隧道底部的沖擊波傳播速度較快，頂部沖擊波在經歷反射疊加作用后，速度也會有一定程度的加快。

2.2 不同爆炸當量下的壓力時程曲線

為研究地鐵區間隧道在爆炸沖擊波作用下的受力特性，實驗時分別在爆炸截面上環形布置28個測點，各測點的截面布置如圖4所示。

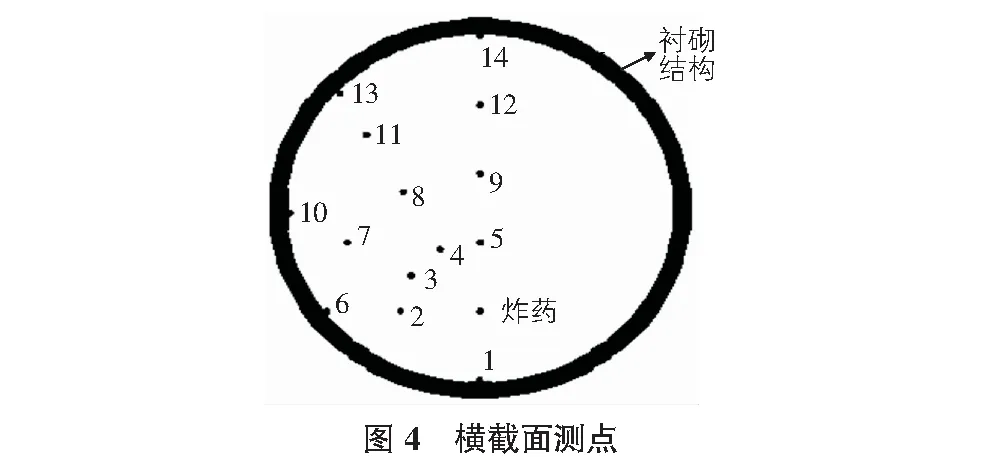
由圖4可以看出，1號～5號測點與爆源炸藥中心的距離為1.1 m；6號～9號測點與爆源炸藥中心的距離為2.2 m；10號～12號測點與爆源炸藥中心的距離為3.3 m；13號測點與爆源炸藥中心的距離為4 m；14號測點與爆源炸藥中心的距離為4.3 m；15號～28號測點距離爆源的直線距離為6 m，其位置與1號～14號測點相對應。

2.2.1 10 kg TNT爆炸當量下的壓力時程曲線

研究裝藥量為10 kg TNT產生的爆炸沖擊波在安裝有復合鋼板地鐵區間隧道的影響特征，并通過壓力時程曲線研究沖擊波的傳播規律。10 kg TNT藥量作用下1號,6號,10號,14號測點的壓力時程曲線如圖5所示。

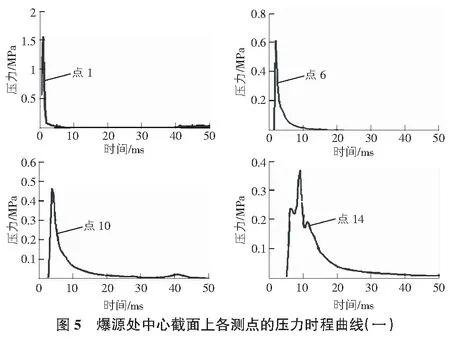
由圖5可以看出，爆炸沖擊波在隧道區間的傳播過程中會產生反射疊加作用，在1號測點處產生最大壓力，數值為1.56 MPa，隨后迅速衰減。6號～9號測點中，在6號測點處產生最大壓力，數值為0.62 MPa；10號～12號測點中，在10號測點處產生最大壓力，數值為0.46 MPa。由此可知，爆炸發生時襯砌結構外側受到較大的壓力作用。由1號和14號測點的壓力時程曲線可以看出：1號測點只出現一次應力峰值，14號測點處歷經多次應力峰值。由于爆炸是瞬時發生的，沖擊波的反射疊加時間非常短暫，因此在1號測點處只出現一個應力峰值，并且1號點的應力值要遠大于其他同距離的4個測點。因爆炸沖擊波在密閉空間內的反射疊加作用，14號測點處會出現多次應力峰值，這與實際情況是一致的。

下面研究距爆源6 m處截面上的15號～28號測點的壓力時程曲線，10 kg TNT爆炸當量作用下爆源截面處15號,20號,24號,28號測點的壓力時程曲線見圖6。

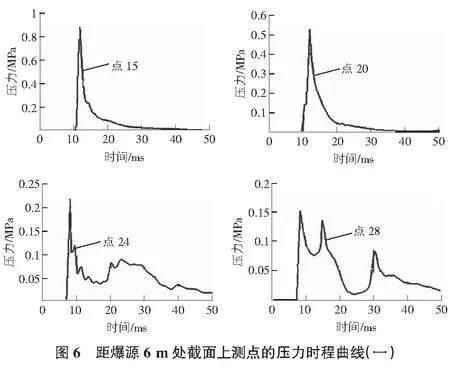
由圖6可以看出，在靠近爆源中心的測點只出現一次峰值，并且持續時間較短；在距離爆源中心超過一定距離后的測點則出現多個峰值。這是因為爆炸沖擊波在傳播過程中會出現多次的反射疊加作用，初始的傳播方向開始發散，導致測點處出現多次峰值。經過多次的反射疊加作用，反射沖擊波的傳播時間隨著反射次數的疊加而逐漸增長，同一直線上各測點的峰值也會隨著沖擊波傳播距離的增加而呈現出逐漸減小的趨勢。

2.2.2 30 kg TNT爆炸當量下的壓力時程曲線

選取測點1號～28號研究30 kg TNT炸藥當量下爆炸產生的沖擊效應，爆源截面處1號,6號,10號,14號測點的壓力時程曲線如圖7所示。

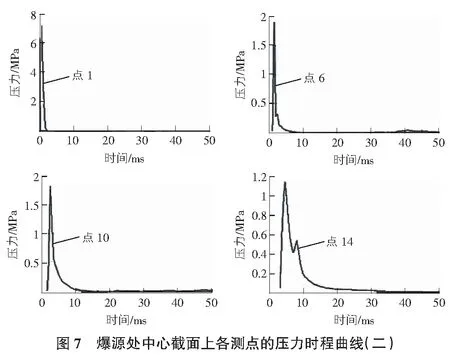
由圖7可以看出，爆炸沖擊波發生反射疊加作用與10 kg TNT爆炸當量作用下的特征相似。爆炸沖擊波的最大應力發生在1號測點，數值為7.28 MPa，隨后迅速衰減；在6號～9號測點中，最大應力發生在6號測點，數值為1.9 MPa；10號～12號測點中，最大應力發生在10號測點，數值為1.7 MPa。由此可知，襯砌結構外側受到的爆炸沖擊作用更強。由圖7中各測點的壓力時程曲線可以看出，部分測點出現多次峰值，相鄰測點的應力變化特征出現較大區別。

通過對比分析30 kg TNT與10 kg TNT炸藥作用下不同測點的壓力時程曲線可知：與爆源中心距離3 m的范圍內出現最大應力，最大應力峰值與炸藥量之間并不是簡單的倍數關系。部分測點在爆炸沖擊作用下出現多次應力峰值，并且二次反射波峰值要高于初次爆炸時的沖擊波峰值。也就是說，這些測點位置處會受到更嚴重的二次破壞。圖8為距離爆源6 m處截面上測點壓力時程曲線。

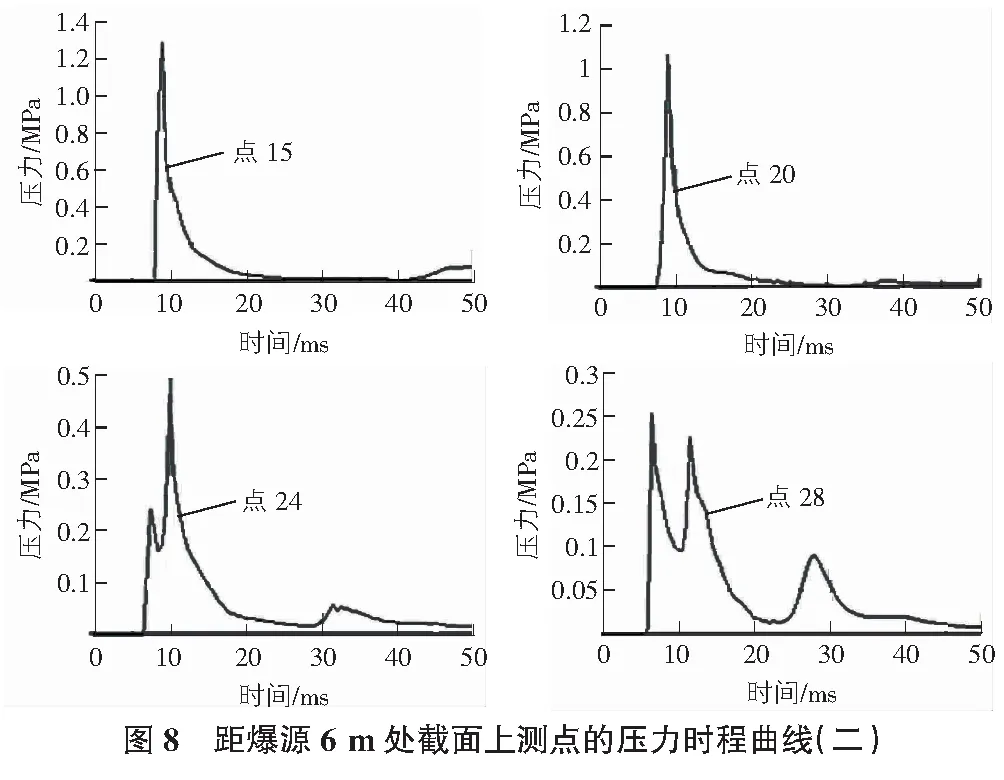
由圖8可以看出，30 kg TNT產生的沖擊波在3 m～6 m距離范圍內出現多次反射疊加，壓力峰值持續出現，之后趨于穩定狀態；當距離超過6 m后，壓力值出現多個峰值，并且持續時間較長；同一距離的30 kg TNT與10 kg TNT各測點峰值增幅之間接近倍數關系。

由兩種不同爆炸當量下的壓力時程曲線可以看出：在距離爆源中心2.2 m的范圍內，最大應力峰值出現在爆源中心線的底部位置，并且明顯高于同距離測點的應力值；在距離爆源中心2.2 m～6 m的范圍內，30 kg TNT與10 kg TNT爆炸當量下的壓力時程曲線具有相似的變化特征，應力值隨著時間的變化逐漸趨于平穩并且呈現出逐漸減弱的趨勢；在距離爆源中心超過6 m的范圍后，在第一峰值處并不一定會出現最大超壓，不同測點處的應力特征也變得更為復雜。

2.3 爆炸產生的超壓沖擊

超壓準則是指當爆炸沖擊波產生的超壓達到或超過一定值后便會對結構造成一定的傷害甚至破壞。目前主要通過爆炸-沖量準則、沖量準則和超壓準則等方法來衡量發生的破壞作用。由于超壓準則較為直觀，因此，隧道結構在受到爆炸沖擊時產生的動力響應可以用超壓準則來分析。選用亨里奇公式計算超壓峰值，將理論值與數值模擬結果進行對比分析，10 kg TNT與30 kg TNT炸藥作用下的超壓沖擊結果分別列于表4，表5。

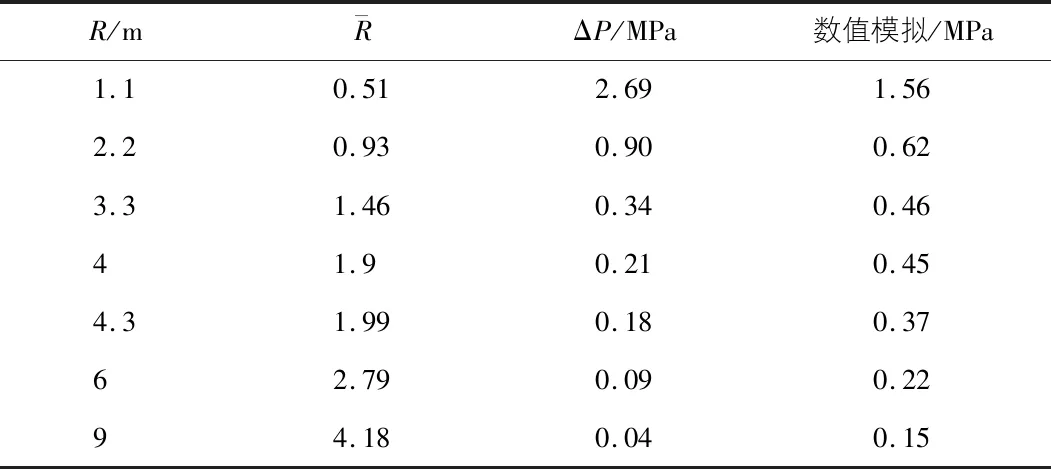
表4 10 kg TNT爆炸作用下超壓峰值

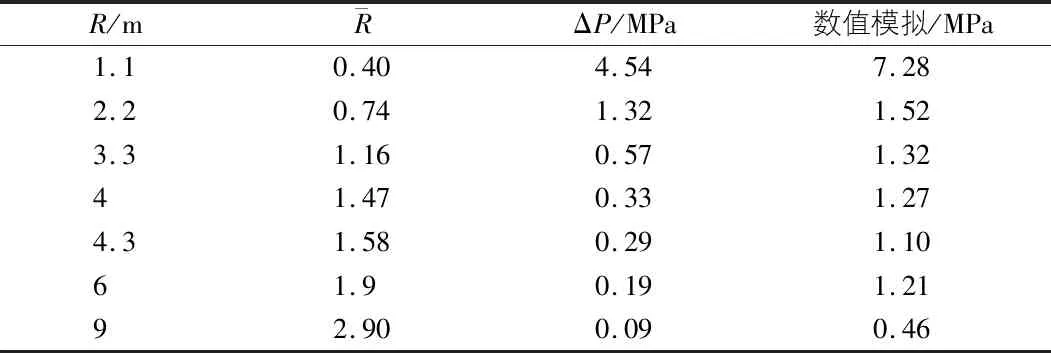
表5 30 kg TNT爆炸作用下超壓峰值

由表4，表5給出的壓力差值可以看出：數值模擬結果與理論計算結果并不是完全吻合的。在10 kg TNT炸藥當量下產生的壓力峰值的模擬值在距離爆源中心較近的范圍內要小于理論值。隨著距離的增加，模擬值與理論值的差值逐漸減小，并且當距離增大到一定程度后模擬值逐漸大于理論值；在30 kg TNT炸藥當量下產生的壓力峰值在距離爆源中心較近的范圍內要大于理論值。兩種計算方式得出的壓力差值隨著距離的增大而逐漸減小。在10 kg TNT和30 kg TNT炸藥當量下，應力峰值在距離爆源中心2.2 m之外的范圍內逐漸趨于穩定狀態并且呈現出明顯的減弱趨勢，這符合爆炸波在隧道區間內傳播的基本特征。

3 結論

1)爆炸沖擊波在地鐵區間隧道的傳播過程中會出現復雜的反射疊加作用，由于爆炸沖擊波的作用，襯砌結構底部出現最大壓力，襯砌結構外側相對于襯砌內部受到較大的壓力作用。部分測點受到沖擊波的反射疊加作用而出現多次應力峰值。2)爆源中心截面處的復合鋼板襯砌結構受到最大的破壞作用。30 kg TNT炸藥當量下爆炸沖擊波的影響范圍更大，使襯砌結構發生顯著的塑性形變，應力峰值隨著距離增加而呈現出逐漸減小的趨勢。3)相同測點的應力峰值隨著傳播距離的減小得到一定程度的增大；10 kg TNT和30 kg TNT炸藥當量下產生的應力峰值分別從1.4 MPa和6.5 MPa增加至1.55 MPa和7.28 MPa；不同測點的應力值隨著時間的推進開始減小并逐漸趨于平穩，這符合爆炸沖擊波傳播的基本規律。