繳志清　郝旭嵐

摘? 要：以2022年全國各地區中考試卷中“圖形與坐標”部分試題為載體，依照課程標準的具體要求，結合試題的特點，從七個不同的角度對“圖形與坐標”專題內容進行分析，并給出解題方法和備考建議. 把握好這類問題的一般性研究策略，有助于提升學生的數學思維品質，同時有助于教師更好地理解中考改革方向.

關鍵詞：圖形與坐標；試題特點分析；優秀試題賞析；備考建議

隨著《義務教育數學課程標準（2022年版）》（以下簡稱《標準》）和《深化新時代教育評價改革總體方案》的頒布，中考改革正在穩步推進.“圖形與坐標”是“圖形與幾何”領域的重要內容，平面直角坐標系是“圖形與坐標”內容的重要組成部分，它是數軸的拓展，是溝通代數與幾何的橋梁. 數形結合、分類討論等思想直指該部分中考數學試題命制思路的本質，指導教師在教學中要不斷優化教學過程，提煉出一般性的思維策略，從而進一步提升學生的數學思維品質.

一、試題特點分析

1. 凸顯核心素養的考查

2022年中考數學試題的命制以《標準》為指導思想，貫徹德智體美勞全面發展的教育方針，落實立德樹人根本任務. 2022年全國各地區中考“圖形與坐標”試題設計靈活多樣，更加注重指向數學核心素養的考查，以達到減少教學中讓學生“機械刷題”的目的. 在落實“雙減”政策、引導教學、減少死記硬背方面做出了新的探索.

2. 展現立德樹人的要求

2022年全國各地區中考“圖形與坐標”試題結合數學學科特點，展現了立德樹人的要求. 例如，湖北宜昌卷第10題以學生的教室平面圖為背景，建立適當的平面直角坐標系，求與小麗相鄰且能比較方便地討論交流的同學座位的坐標，這既要求學生養成平時善于觀察的學習習慣，又讓學生體會到了討論交流是促進學習發展的一種很好的手段.

3. 體現數學與實際生活的融合

2022年全國各地區中考“圖形與坐標”試題還展現了數學在實際生活中的應用. 例如，山東煙臺卷第12題和湖北鄂州卷第14題都是以象棋棋盤為背景，建立適當的平面直角坐標系，求某棋子的坐標. 這兩道試題把平面直角坐標系與象棋文化相結合，考查了學生應用數學知識解決實際生活問題的能力.

4. 落實課程標準的要求和數學本質的考查

初中階段，“圖形與幾何”領域包括“圖形的性質”“圖形的變化”和“圖形與坐標”三個主題，分別從演繹證明、運動變化、量化分析三個方面研究圖形的基本性質和相互關系. 這三個方面的知識又是相輔相成、相互影響的. 因此，試題的呈現形式要綜合這三個方面的知識.《標準》中，“圖形與坐標”的具體內容包括兩個方面：一是圖形的位置與坐標；二是圖形的運動與坐標.

2022年全國各地區中考“圖形與坐標”試題的考查符合《標準》要求，關注數學本質，立足學生數學核心素養的發展. 例如，天津卷第10題將一個等腰三角形與平面直角坐標系相結合，考查了三角形各個頂點的位置；山東泰安卷第14題將平行四邊形與平面直角坐標系相結合，考查平行四邊形的性質、點和線段的平移規律. 這些試題都重點考查了學生的理性思維能力及分析和解決問題的能力. 對于“圖形與坐標”部分的試題，必須利用好平面直角坐標系這個溝通代數與幾何的橋梁，學會用坐標表示圖形上點的位置、用坐標表達圖形的變化、用坐標表達簡單圖形的性質，即用代數方法研究圖形，體會數形結合的數學思想，提高分析和解決問題的能力.

二、優秀試題分析

2022年全國各地區中考數學試卷中，“圖形與坐標”內容主要考查的知識點包括以下幾個方面：（1）用坐標表示圖形的位置；（2）用坐標表示圖形的性質；（3）用坐標表示圖形的變化；（4）用坐標表示動點的變化規律；（5）用坐標表示動點的函數圖象；（6）平面直角坐標系中圖形性質與函數圖象的綜合問題；（7）平面直角坐標系中的作圖問題；等等. 該部分試題的考查形式靈活，涉及選擇題、填空題、解答題，其中蘊含了數形結合、分類討論、轉化、建模等數學思想，以及推理能力、幾何直觀、空間觀念、模型觀念等素養.

1. 用坐標表示圖形的位置

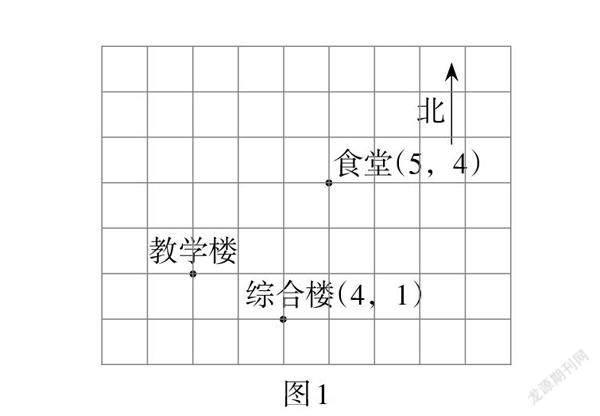
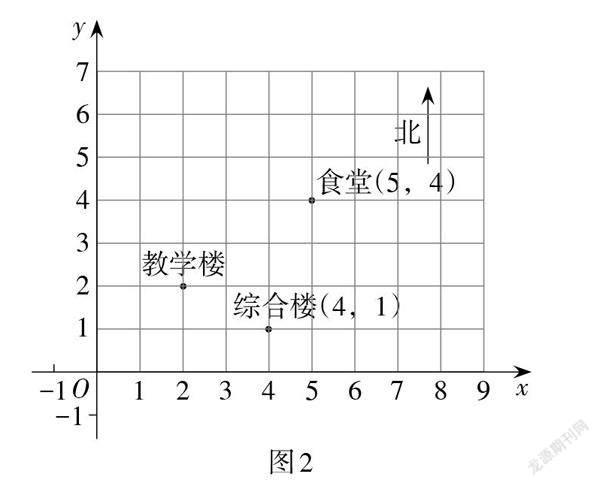
例1 （廣西·柳州卷）如圖1，這是一個利用平面直角坐標系畫出的某學校的示意圖，如果這個坐標系分別以正東、正北方向為x軸、y軸的正方向，并且綜合樓和食堂的坐標分別是（4，1）和（5，4），則教學樓的坐標是（? ）.

（A）（1，1） （B）（1，2）

（C）（2，1） （D）（2，2）

目標解析：此題主要考查在實際問題中建立適當的平面直角坐標系描述物體的位置. 這類試題直接考查點的位置與坐標，以及基礎知識和基本技能，屬于簡單題.

解法分析：如圖2，根據綜合樓和食堂的坐標分別是（4，1）和（5，4），建立適當的平面直角坐標系，可得教學樓的坐標是（2，2）. 故此題答案選D．

試題分析：這類試題一般源于教材，在教材課后習題的基礎上進行改編. 平面上的點與坐標之間是一一對應關系，根據兩個點的坐標可以建立適當的平面直角坐標系，然后再用坐標描述點的位置. 根據題意建立適當的平面直角坐標系是解決此類試題的關鍵．

類題賞析：類似的試題還有山東煙臺卷第12題、浙江金華卷第7題、湖北宜昌卷第10題、甘肅蘭州卷第14題等，這些試題體現了實際生活與數學相聯系的特點，體現了數學既源于生活，又應用于生活.

2. 用坐標表示圖形的性質

例2 （天津卷）如圖3，△OAB的頂點O（0，0），頂點A，B分別在第一、四象限，且AB⊥Ox，若AB = 6，OA = OB = 5，則點A的坐標是（? ）.

（A）（5，4） （B）（3，4）

（C）（5，3） （D）（4，3）

目標解析：此題考查的是圖形的性質與坐標，以及學生的推理能力和運算能力，旨在發展學生的幾何直觀素養.

解法分析：如圖4，設AB與x軸交于點C.

因為OA = OB，OC⊥ AB，AB = 6，

所以AC =[12]AB = 3.

由勾股定理，得OC =[OA2-AC2=52-32]= 4.

所以點A的坐標為（4，3）.

故此題選擇D．

試題分析：此題是求點的坐標. 解題思路是先根據題意求出線段OC的長，再根據點的位置確定這個點的坐標. 解題過程中用到了等腰三角形“三線合一”的性質和勾股定理. 這類試題的考查難度一般較小，但是涉及的圖形性質較多，需要在熟練掌握圖形性質的基礎上求線段的長度，從而得出點的坐標.

類題賞析：類似地，青海卷第5題、吉林卷第12題、貴州銅仁卷第2題、貴州黔西南州卷第10題也考查了圖形的性質與坐標的知識. 其中，吉林卷第12題還考查了圓的垂徑定理.

3. 用坐標表示圖形的變化

（1）坐標與圖形的對稱.

例3 （浙江·麗水卷）三個能夠重合的正六邊形的位置如圖5. 已知點B的坐標是（[-3]，3），則點A的坐標是? ? ? ?．

目標解析：此題主要是用坐標描述幾何圖形的對稱性，考查學生的幾何直觀素養.

解法分析：根據正六邊形的性質，可得點A和點B關于原點對稱. 因為點B的坐標是（[-3]，3），所以點A的坐標是（[3]，-3）. 故此題的答案為（[3]，-3）．

試題分析：此題中，利用正六邊形的對稱性能夠知道點A和點B關于原點對稱. 解決這類試題既要能準確判斷圖形的對稱性，還要熟練掌握關于x軸、y軸、原點對稱的點的坐標特點.

類題賞析：類似地，浙江臺州卷第6題也考查了坐標與圖形的對稱的知識.

（2）坐標與圖形的平移.

例4 （山東·臨沂卷）如圖6，在平面直角坐標系中，△ABC的頂點A，B的坐標分別是A（0，2），B（2，-1）. 平移△ABC得到△A′B′C′，若點A的對應點A′的坐標為（-1，0），則點B的對應點B′的坐標是

目標解析：此題考查的是用坐標描述圖形的平移. 這類試題利用平面直角坐標系將幾何與代數完美地結合在了一起，充分體現了數形結合思想.

解法分析：由題意可知，將點A從（0，2）平移至（-1，0），可以看作是將△ABC先向下平移2個單位長度，再向左平移1個單位長度（或者先向左平移1個單位長度，再向下平移2個單位長度）. 再由點B的坐標為B（2，-1），可得平移后的對應點為B′（1，-3）. 故此題的答案為（1，-3）．

試題分析：此題由點A的平移可以判斷出點B的平移規律，從而利用平移前后點的坐標特點來解決問題. 解決這類試題最重要的是掌握平移的性質和平移前后對應點坐標的變化規律.

類題賞析：類似地，山東泰安卷第14題、遼寧大連卷第13題、廣西百色卷第10題、山東威海卷第6題等也考查了坐標與圖形平移的知識點. 其中，山東泰安卷第14題需要利用平行四邊形兩組對邊分別平行的性質，可以看作將線段DC平移到線段AB，從而利用平移的性質解決問題.

（3）坐標與圖形的旋轉.

例5 （黑龍江·綏化卷）如圖7，線段OA在平面直角坐標系內，點A坐標為A（2，5），線段OA繞原點O逆時針旋轉90°，得到線段OA′，則點A′的坐標為（? ）.

目標解析：此題考查的是用坐標描述圖形的旋轉. 學生在解決此類問題時，要靈活應用相關知識點，體會各個知識點之間的聯系，以及數學思維的深刻性，彰顯數學的本質.

解法分析：如圖8，過點A作AB⊥Ox于點B，過點A′作A′C⊥Ox于點C.

因為點A的坐標為A（2，5），

所以OB = 2，AB = 5.

由題意，得∠AOA′ = 90°，OA = OA′．

所以∠AOB + ∠A′OC = 90°．

因為∠A′OC + ∠A′ = 90°，

所以∠A′ = ∠AOB．

在△A′OC和△OAB中，

因為[∠A′= ∠AOB，∠A′CO=∠OBA=90°，OA′=AO，]

所以△A′OC ≌ △OAB（AAS）．

所以A′C = OB = 2，OC = AB = 5.

所以點A′的坐標為（-5，2）．

故此題選擇A．

試題分析：此題是在過點A作AB⊥Ox于點B，過點A′作A′C⊥Ox于點C后，利用“一線三等角”和三角形全等，求出A′C和OC的長度，從而得出點A′的坐標. 這類試題往往具有以下特點：（1）旋轉角度為特殊角或者旋轉到某個特殊位置；（2）問題設置一般是求圖形旋轉前后點的坐標；（3）有時會在網格的背景下進行旋轉. 解決這類試題常作的輔助線是過某點向x軸或y軸作垂線，利用圖形的性質求解相應的線段長度，這是解題的關鍵. 這里要注意抓住旋轉的兩大特點：（1）對應點到旋轉中心的距離相等；（2）兩組對應點分別與旋轉中心的連線所夾的角相等. 解決此類問題時還經常會用到三角形全等的性質和勾股定理等知識.

類題賞析：類似地，江蘇蘇州卷第8題、黑龍江牡丹江卷第19題、四川內江卷第9題、湖南湘潭卷第17題也考查了坐標與圖形旋轉的知識點. 其中，江蘇蘇州卷第8題要分別過點C作x軸、y軸的垂線段，然后利用等邊三角形的性質和勾股定理，把相關線段的長度用含m的代數式進行表示，再利用線段之間的關系建立方程模型，求出m的值．

（4）坐標與圖形的位似.

例6 （貴州·黔西南州卷）如圖9，在平面直角坐標系中，△OAB與△OCD位似，位似中心是坐標原點O. 若點A（4，0），點C（2，0），則△OAB與△OCD周長的比值是? ? ? ?．

目標解析：此題考查的是用坐標描述圖形的位似，以及學生的識圖能力，旨在發展學生的幾何直觀素養.

解法分析：因為△OAB與△OCD位似，位似中心是坐標原點O，而點A（4，0），點C（2，0），

所以相似比為4∶2 = 2∶1.

所以△OAB與△OCD周長的比值為2．

故此題的答案為2．

試題分析：此題考查平面直角坐標系中的圖形位似的問題. 如果位似變化是以原點為位似中心，相似比為k，那么位似圖形對應點的坐標之比等于k或-k．熟練掌握位似變化前后點的坐標的變化規律，是解決此類問題的關鍵.

類題賞析：類似地，四川巴中卷第6題也考查了位似圖形與平面直角坐標系相結合的問題.

（5）坐標與銳角三角函數.

例7 （湖北·荊州卷）如圖10，在平面直角坐標系中，點A，B分別在x軸負半軸和y軸正半軸上，點C在OB上，OC∶BC = 1∶2，連接AC，過點O作OP∥AB交AC的延長線于點P．若P（1，1），則tan∠OAP的值是（? ? ）.

（A） [33] （B） [22]

（C） [13] （D） 3

目標解析：此題屬于圖形的變化與坐標的內容，這里主要考查的是坐標與銳角三角函數的結合.

解法分析：如圖11，過點P作PQ⊥Ox于點Q，

因為OP∥AB，

所以∠CAB = ∠CPO，∠ABC = ∠COP.

所以△OCP ∽ △BCA.

所以CP∶AC = OC∶BC = 1∶2 .

因為∠AOC = ∠AQP = 90°，

所以CO∥PQ.

所以OQ∶AO = CP∶AC = 1∶2 .

因為P（1，1），所以PQ = OQ = 1.

所以AO = 2.

所以tan∠OAP =[PQAQ=12+1=13].

故此題答案選C.

試題分析：解決這類試題的關鍵是根據題目的已知條件發現圖形中的相似或全等模型，利用常用的輔助線作法“向坐標軸作垂線”構建直角三角形，利用圖形的性質求解相關線段的長度，然后利用銳角三角函數的定義解決問題.

類題賞析：四川瀘州卷第11題也考查了平面直角坐標系與銳角三角函數相結合的問題.

4. 用坐標表示動點的變化規律

例8 （河南卷）如圖12，在平面直角坐標系中，邊長為2的正六邊形ABCDEF的中心與原點O重合，AB∥Ox，交y軸于點P. 將△OAP繞點O順時針旋轉，每次旋轉90°，則第2 022次旋轉結束時，點A的坐標為（? ）.

（A）（[3]，-1） （B）（-1，[-3]）

（C）（[-3]，-1） （D）（1，[3]）

目標解析：此題主要考查點的運動與坐標的變化規律，以及學生的觀察能力、推理能力、歸納概括能力等，屬于綜合類試題.

解法分析：如圖13，由正六邊形的性質可得A（1，[3]）. 再由每次旋轉90°，可知每旋轉4次為一個循環. 由2 022 ÷ 4 = 505…2，可知點A2 022與點A2重合，故求出點A2的坐標可得答案. 因為點A2與點A關于原點O對稱，所以A2（-1，[-3]）. 因此第2 022次旋轉結束時，點A的坐標為（-1，[-3]）. 故此題答案選B.

試題分析：此題以正六邊形為背景，由正六邊形的性質可以得出坐標的變化規律．解決這類試題的關鍵是正確識別圖形，利用圖形的性質等知識找到動點的變化規律，難度較大.

類題賞析：類似地，黑龍江齊齊哈爾卷第17題、貴州畢節卷第20題、湖北荊門卷第15題、貴州黔西南州卷第20題、山東菏澤卷第14題也都考查了坐標與動點的變化規律. 其中，黑龍江齊齊哈爾卷第17題先利用函數解析式可得點A，B的坐標，從而得出∠BAO = 30°，進而根據三角函數的定義，得出點的坐標的變化規律，最終得到答案.

5. 用坐標表示動點的函數圖象

例9 （山東·濰坊卷）如圖14，在[?]ABCD中，∠A = 60°，AB = 2，AD = 1，點E，F在?ABCD的邊上，從點A同時出發，分別沿A→B→C和A→D→C的方向以每秒1個單位長度的速度運動，到達點C時停止，線段EF掃過區域的面積記為y，運動時間記為x，能大致反映y與x之間函數關系的圖象是（? ）.

目標解析：此題主要考查的是動點的函數圖象問題. 這類試題考查學生的畫圖、識圖能力，以及分析問題和解決問題的能力，屬于綜合類試題，難度較大.

解法分析：過點F作FH⊥AB于點H. 如圖15，當0 ≤ x ≤ 1時，在Rt△FAH中，AF = x，∠A = 60°，則FH = AF·sin A =[32]x. 所以線段EF掃過區域的面積y =[12]x·[32]x =[34]x2，圖象是開口向上的拋物線的一部分.

如圖16，當1 < x ≤ 2時，過點D作DP⊥AB于點P，則DP = AD·sin A =[32]. 所以線段EF掃過區域的面積y =[12]（x - 1 + x） ×[32]=[32x]-[34]，圖象是y隨x的增大而增大的線段.

如圖17，當2 < x ≤ 3時，過點E作EG⊥CD于點G，則CE = CF = 3 - x. 所以EG =[32]（3 - x）. 所以線段EF掃過區域的面積y = 2 ×[32-12]（3 - x） ×[32]（3 - x） =[3-34]（3 - x）2，圖象是開口向下的拋物線的一部分.

試題分析：此題以平行四邊形為背景，考查了動點問題中的函數圖象、平行四邊形的性質、三角形的性質、一次函數和二次函數的圖象及性質，具有較強的綜合性. 解決此類問題的關鍵是根據圖形的特點和動點的運動情況進行分類討論，通過分析各個時間段的圖形特點，分別寫出各個時間段的函數表達式. 在考場上，對于此類選擇題，有時候并不需要寫出最終的函數表達式，可以通過排除法判斷各個時間段的函數圖象特點，從而得出答案.

類題賞析：遼寧鞍山卷第8題、山東菏澤卷第8題、內蒙古鄂爾多斯卷第10題都考查了動點的函數圖象問題.

6. 平面直角坐標系中圖形性質與函數圖象的綜合問題

例10 （四川·瀘州卷）如圖18，在平面直角坐標系xOy中，矩形OABC的頂點B的坐標為（10，4），四邊形ABEF是菱形，且tan∠ABE =[43]. 若直線l把矩形OABC和菱形ABEF組成的圖形的面積分成相等的兩部分，則直線l的解析式為（? ）.

（A）y = 3x （B）y =[-34x+152]

（C）y = -2x + 11 （D）y = -2x + 12

目標解析：此題考查的是坐標與圖形的性質和函數圖象相結合的綜合問題. 這類試題考查了學生的推理能力及建立函數模型的能力，是對數學核心素養的深度考查.

解法分析：如圖19，連接OB，AC，交于點M，連接AE，BF，交于點N，則直線MN為符合條件的直線l.

因為四邊形OABC是矩形，所以OM = BM．

因為點B的坐標為B（10，4），

所以M（5，2），AB = 10，BC = 4．

因為四邊形ABEF為菱形，所以BE = AB = 10．

過點E作EG⊥AB于點G，

在Rt△BEG中，因為tan∠ABE =[43]，所以[EGBG=43].

設EG = 4k，則BG = 3k.

所以BE =[EG2+BG2]= 5k.

因為5k = 10，所以k = 2.

所以EG = 8，BG = 6. 所以AG = 4．

所以E（4，12）．

因為點B的坐標為B（10，4），且AB∥Ox，

所以A（0，4）．

因為點N為AE的中點，所以N（2，8）．

設直線l的解析式為y = ax + b（a ≠ 0），

所以[5a+b=2，2a+b=8.] 解得[a=-2，b=12.]

所以直線l的解析式為y = -2x + 12.

故此題選擇D．

試題分析：此題要平分一個矩形和一個菱形所組合圖形的面積，利用兩個圖形的中心對稱性質，分別求出矩形OABC和菱形ABEF的中心的坐標，利用待定系數法，求經過兩個圖形中心的直線解析式即可得到答案. 解決此類問題的關鍵是充分利用圖形的性質和函數圖象性質求解出特殊點的坐標，難度較大.

類題賞析：類似地，黑龍江齊齊哈爾卷第15題、浙江紹興卷第15題、浙江寧波卷第16題、四川樂山卷第16題等，都考查了平面直角坐標系中的綜合問題.

7. 平面直角坐標系中的作圖問題

例11 （廣西·河池卷）如圖20，在平面直角坐標系中，△ABC的三個頂點的坐標分別為A（4，1），B（2，3），C（1，2）．

（1）畫出與△ABC關于y軸對稱的△A1B1C1；

（2）以原點O為位似中心，在第三象限內畫一個△A2B2C2，使它與△ABC的相似比為2∶1，并寫出點B2的坐標．

目標解析：此題考查了在平面直角坐標系和網格中的作圖問題. 此題既考查了作軸對稱圖形和位似圖形. 除此之外，還可以考查作中心對稱圖形、旋轉后的圖形等. 這類試題主要考查學生的動手操作能力，要想畫出準確的圖形，必須熟練掌握圖形的性質.

解法分析：（1）如圖21，△A1B1C1為所求；

（2）如圖21，△A2B2C2為所求，點B2的坐標為（-4，-6）.

試題分析：此類試題還可以與圓的知識結合，如弧長公式、扇形的面積等. 解決這類問題的關鍵是掌握圖形變化前后的坐標變化規律，先確定關鍵點，再確定圖形.

類題賞析：陜西卷第19題、黑龍江龍東地區卷第22題也考查了在平面直角坐標系和網格中的作圖問題.

三、復習備考建議

1. 注重基礎，回歸數學本質

“圖形與坐標”這部分內容的本質是用坐標表達圖形的性質和圖形的對稱、旋轉、平移變化的規律. 在中考復習備考時，教師要引導學生回歸數學本質，注重基礎知識. 學生要熟練掌握三角形、平行四邊形、矩形、菱形、正方形等基本圖形的性質；充分理解平面直角坐標系中各象限點的坐標特點，以及將圖形進行對稱、平移、旋轉變化時坐標的變化規律；要熟練掌握建立平面直角坐標系、描點、畫圖等基本操作. 復習這些基礎知識時，要以教材為主，充分發揮教材的導向作用；要重視坐標與圖形的性質和變化等知識之間的聯系，從“大單元”的角度深度學習，注重知識的整體性. 教師要引導學生用好平面直角坐標系這個聯系代數和幾何的橋梁，能用代數方法表達圖形的性質和變化.

例如，內蒙古赤峰卷第18題考查了拋物線與[x]軸的交點、二次函數圖象上點的坐標特征、等腰直角三角形的判定與性質、軸對稱的性質等知識. 解決此類問題的關鍵是熟練掌握二次函數圖象上點的坐標特征、軸對稱性質等數學本質內容．解決此題不僅要利用數形結合思想直觀感知試題中的一些關系，而且要注意利用二次函數進行計算和說理時，需要在求函數解析式的基礎上進行邏輯推理，從而探究出所求點的坐標. 這也落實了《標準》中的新增內容——了解代數推理.

2. 注重方法，提高思維品質

眾所周知，數學是思維的科學，數學是思維的體操. 數學教學的核心任務之一是要培養學生的思維能力，使學生在掌握數學基礎知識的過程中，學會感知、觀察、歸納、類比、想象、抽象、概括、推理、證明和反思的邏輯思考的基本方法.

對于“圖形與坐標”這部分內容，在復習備考時，要注意解題方法的提煉. 在解題時，要注意對條件展開合理的聯想，形成條件關系網. 例如，看到求點的坐標的題目，對條件展開聯想：能否作坐標軸的垂線？能否構造三角形全等或相似？能否利用勾股定理建立方程？對于給出的一個問題需要嘗試從不同的角度去思考，從而得出不同的解決問題的方法.

數學學習是一個不斷優化的過程，只有通過不同方法的比較，才能優化解題的思路. 在平時做題時，學生要注意總結如何思考、如何轉化、如何作輔助線等問題，使數學學習超越具體的知識和技能，由反思解決具體題目的過程和方法，過渡到提煉出一般性的思維策略，在訓練過程中把邏輯思維能力推向多方向、多層次，舉一反三，觸類旁通，從題海中解脫出來，從而減輕學習負擔，進一步提升數學思維的品質.

3. 注重理解，提升運算能力

《標準》指出：運算能力，主要是指根據法則和運算律進行正確運算的能力. 能夠明晰運算的對象和意義，理解算法與算理之間的關系；能夠理解運算的問題，選擇合理簡潔的運算策略解決問題；能夠通過運算促進數學運算能力的發展，運算能力有助于形成規范化思考問題的品質，養成一絲不茍、嚴謹求實的科學態度.

“圖形與坐標”這部分的試題往往需要結合勾股定理、銳角三角函數、三角形全等或相似、圓的相關性質、弧長和扇形面積公式等知識，求解相關線段的長度或圖形的面積. 在這個過程中會應用到解方程、二次根式的化簡、銳角三角函數的計算等代數推理. 因此，提升運算能力對這部分試題的解答會有很大的幫助. 在復習備考過程中，要認真總結運算錯誤的原因，如公式記憶不準、缺乏簡便運算的技巧、算理不清等. 例如，對弧長及扇形面積公式記憶不準確，導致計算錯誤. 對此，在學習時要重視公式的形成過程，在徹底了解公式的來龍去脈后，對公式的記憶會更加準確，即便生疏了，自己也能推導出來. 又如，用勾股定理計算PA7 =[242-122]，可以運用平方差公式進行簡便計算，即[242-122=24+12×24-12=][36×12=123]. 這樣的運算過程顯然計算量更小，不易出錯. 所以在學習平方差公式或者勾股定理的課程時，要注意掌握類似的計算方法，提高運算的準確性，從而提升運算能力.

四、典型模擬題

以上總結了2022年全國各地區中考試卷針對“圖形與坐標”這一模塊的考查方向，下面向大家展示四道模擬試題，有不妥之處，還望各位同仁批評指正.

1. 點[M-tan60°，cos45°]關于[x]軸對稱的點的坐標是（? ? ）.

（A）[32， 12] （B）[-33，-12]

（C）[-3， 22] （D）[-3，-22]

答案：D.

【評析】此題將點的坐標與三角函數相結合，考查了學生對相關基礎知識的掌握情況.

2. 在平面直角坐標系中，直線y = 2x + 3與x軸的交點坐標是（? ? ）.

（A）（0，3） （B）（3，0）

（C）[0，-32] （D）[-32，0]

答案：D.

【評析】此題考查了一次函數與坐標軸的交點坐標，是對學生基礎知識和基本技能的考查.

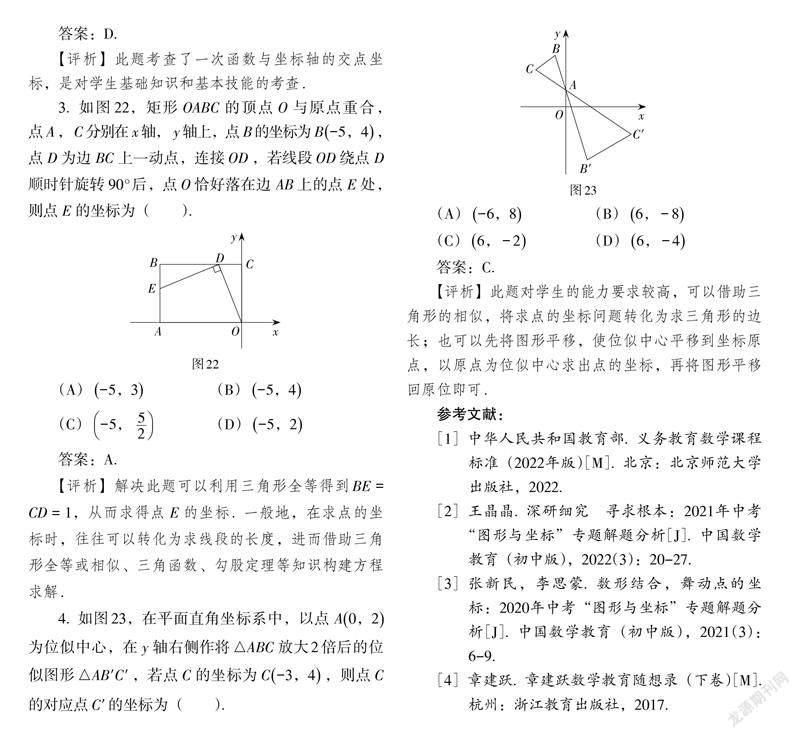
3. 如圖22，矩形[OABC]的頂點[O]與原點重合，點[A]，[C]分別在[x]軸，[y]軸上，點[B]的坐標為[B-5，4]，點[D]為邊[BC]上一動點，連接[OD]，若線段[OD]繞點[D]順時針旋轉[90°]后，點[O]恰好落在邊[AB]上的點[E]處，則點[E]的坐標為（? ? ）.

（A）[-5，3] （B）[-5，4]

（C）[-5， 52] （D）[-5，2]

答案：A.

【評析】解決此題可以利用三角形全等得到BE = CD = 1，從而求得點[E]的坐標. 一般地，在求點的坐標時，往往可以轉化為求線段的長度，進而借助三角形全等或相似、三角函數、勾股定理等知識構建方程求解.

4. 如圖23，在平面直角坐標系中，以點[A0，2]為位似中心，在[y]軸右側作將[△ABC]放大2倍后的位似圖形[△AB′C′]，若點[C]的坐標為[C-3，4]，則點[C]的對應點[C′]的坐標為（? ? ）.

（A）[-6，8] （B）[6，-8]

（C）[6，-2] （D）[6，-4]

答案：C.

【評析】此題對學生的能力要求較高，可以借助三角形的相似，將求點的坐標問題轉化為求三角形的邊長；也可以先將圖形平移，使位似中心平移到坐標原點，以原點為位似中心求出點的坐標，再將圖形平移回原位即可.

參考文獻：

［1］中華人民共和國教育部. 義務教育數學課程標準（2022年版）［M］. 北京：北京師范大學出版社，2022.

［2］王晶晶. 深研細究? 尋求根本：2021年中考“圖形與坐標”專題解題分析［J］. 中國數學教育（初中版），2022（3）：20-27.

［3］張新民，李思蒙. 數形結合，舞動點的坐標：2020年中考“圖形與坐標”專題解題分析［J］. 中國數學教育（初中版），2021（3）：6-9.

［4］章建躍. 章建躍數學教育隨想錄（下卷）［M］. 杭州：浙江教育出版社，2017.

作者簡介：繳志清（1961— ），男，正高級教師，主要從事課程、教學與考試評價研究；

郝旭嵐（1971— ），女，高級教師，主要從事中學數學教學研究.