陳耀忠　孫陳威

摘? 要：“圖形的變化”是初中數學“圖形與幾何”領域的重要內容，是在研究幾何圖形的本質屬性之后對圖形變化規律的進一步探索和研究. 文章通過對2022年全國各地區中考數學試卷中“圖形的變化”典型試題，從學業要求、解法分析、試題分析和類題評析四個維度進行闡述、解析、評價，充分展示了探尋基本圖形和圖形在運動變化中不變量的一般過程. 分析發現，在“圖形的變化”問題解決中，只有重視教材、回歸教材、夯實基礎、提升能力，才能以不變應萬變.

關鍵詞：圖形的變化；典型試題；解法分析

《義務教育數學課程標準（2022年版）》（以下簡稱《標準》）對“圖形的變化”內容明確了學業要求，對引導學生會用數學的眼光觀察現實世界、會用數學的思維思考現實世界、會用數學的語言表達現實世界具有重要意義.

如何達到《標準》明確的學業要求？如何求解“圖形的變化”試題？本文立足解題評價視角，從考點概述、典題分析、備考建議三個方面對選取的“圖形的變化”典型試題進行剖析總結，以期對中考復習備考提供參考.

一、考點概述

1. 學業要求

“圖形的變化”內容隸屬于初中階段“圖形與幾何”領域，其內容主要包括圖形的軸對稱、旋轉、平移、相似、投影、銳角三角函數.《標準》對本部分內容的學習要求如圖1所示.

2. 考查特點

從2022年全國各地區中考數學試卷對“圖形的變化”專題內容的考查情況來看，該部分內容考查的題型涉及填空題、選擇題、解答題、操作題等，且各地區中考對“圖形的變化”內容的考查都很重視. 研究發現，2022年全國各地區中考“圖形的變化”試題考查具有以下特點：（1）立足教材，關注對基本概念的理解和運用；（2）盡可能設置生活化的實際背景，考查學生運用數學知識解決實際問題的能力，以及在解決實際問題的過程中學生所表現出來的數學思維方式；（3）重視對幾何直觀、空間觀念、邏輯推理等素養的落實情況進行考查.

二、優秀試題分析

2022年全國各地區中考對“圖形的變化”試題的命制整體上呈起點低、坡度緩、立意高的特點，符合《標準》要求，既立足對圖形的軸對稱、旋轉、平移、相似、投影等基礎內容的考查，又關注學生的未來發展，考查學生對同一知識點的不同認知水平，多角度、多維度考查學生的空間觀念、幾何直觀、推理能力等素養. 下面從學業要求、解法分析、試題分析和類題評析四個維度對2022年中考“圖形的變化”試題進行解題分析.

1. 依標扣本，考查基礎，強化空間觀念

課程標準是中考數學試題命制的依據，教材是中考數學試題命制的藍本. 立足“三會”、依標扣本是2022年中考“圖形的變化”試題命制方面的典型特征.

例1 （甘肅·蘭州卷）下列分別是2022年北京冬奧會、1998年長野冬奧會、1992年阿爾貝維爾冬奧會、1984年薩拉熱窩冬奧會會徽上的圖案，其中是軸對稱圖形的是（? ? ）.

學業要求：理解幾何圖形的對稱性，感悟現實世界中的對稱美.

解法分析：此題選取四屆冬奧會會徽上的圖案為素材，要求判斷其是否為軸對稱圖形，解題的關鍵是辨別哪個圖形沿某一條直線對折后，直線兩旁的部分能夠完全重合. 此題答案選D.

試題分析：此題既考查學生對基本概念的把握情況、對軸對稱圖形的認識，又考查學生在具體情境中應用軸對稱圖形概念的能力.

類題賞析：2022年全國各地區中考試卷中此類試題的命制大致選擇圖案設計、文字數字、剪紙藝術、幾何圖形四類. 其中，山東泰安卷第3題、江蘇連云港卷第2題、四川內江卷第4題、貴州畢節卷第2題、黑龍江齊齊哈爾卷第2題、黑龍江大慶卷第4題等以圖案設計類為考查對象；天津卷第4題、湖北武漢卷第3題、四川樂山卷第2題以漢字為考查對象；四川眉山卷第3題以英文字母為考查對象；湖北宜昌卷第2題以數字為考查對象；山東臨沂卷第2題、湖南永州卷第3題以剪紙藝術為考查對象；廣西桂林卷第4題、黑龍江哈爾濱卷第3題、四川遂寧卷第2題以幾何圖形為考查對象.

例2 （浙江·溫州卷）某物體如圖2所示，它的主視圖是（? ? ）.

學業要求：經歷從不同角度觀察立體圖形的過程，發展學生的幾何直觀和空間觀念.

解法分析：解決此題需要掌握主視圖就是從正面看物體所得到的圖形. 此題答案選D.

試題分析：此題考查給定幾何體甄別三視圖，重在考查簡單組合體的主視圖.

類題賞析：2022年中考湖南邵陽卷第4題、湖北武漢卷第5題、浙江臺州卷第2題、天津卷第5題、浙江嘉興卷第2題、湖南衡陽卷第2題、浙江湖州卷第3題、江西卷第5題、安徽卷第3題均為此類試題或此種考法，而湖北孝感卷第2題、江蘇揚州卷第5題考查給定三視圖甄別幾何體. 還有一些地區的中考試卷中雖然也是給定幾何體，但是問法更加靈活，提出了“主視圖與俯視圖的形狀不一樣的幾何體是什么”“幾何體的三視圖中完全相同的是什么”等問題. 此類問題的難度略高于上述問題，需要學生牢固掌握幾何體的三種視圖.

例3 （新疆卷）圖3是某幾何體的展開圖，該幾何體是（? ? ）.

（A）長方體 （B）正方體

（C）圓錐 （D）圓柱

學業要求：知道簡單立體圖形的側面展開圖，發展學生的幾何直觀和空間觀念.

解法分析：解決此題的關鍵是“熟練掌握圓錐的側面展開圖是扇形、底面是圓形”. 此題答案選C.

試題分析：此題考查依據給定簡單幾何體的側面展開圖甄別幾何體，題面簡潔、圖形明了.

類題賞析：2022年中考四川廣元卷第2題、江蘇宿遷卷第4題、湖南岳陽卷第2題、四川自貢卷第3題均為此類考法. 綜觀2022年全國各地區中考試卷中“圖形的變化”試題，基本都是結合圓柱、圓錐、長方體等常見幾何體的側面展開圖進行命題，考查學生的幾何直觀素養和空間想象能力.

例4 （安徽卷）如圖4，在由邊長為1個單位長度的小正方形組成的網格中，△ABC的頂點均為格點（網格線的交點）.

（1）將△ABC向上平移6個單位，再向右平移2個單位，得到[△A1B1C1]，試畫出[△A1B1C1]﹔

（2）以邊AC的中點O為旋轉中心，將△ABC按逆時針方向旋轉180°，得到[△A2B2C2]，試畫出[△A2B2C2].

學業要求：理解平移、旋轉運動，知道平移、旋轉的基本特征.

解法分析：解決此題需要根據平移的方式確定出點A1，B1，C1的位置，再順次連接，即可得到[△A1B1C1]. 再根據旋轉可確定出點A2，B2，C2的位置，再順次連接，即可得到[△A2B2C2]. 所作[△A1B1C1]和[△A2B2C2]如圖5所示.

試題分析：此題考查運用作圖法分析圖形平移和旋轉變化后的性質特點，引導學生經歷平移和旋轉的作圖過程，構建平移、旋轉知識經驗，鞏固作圖技能.

類題賞析：2022年中考浙江溫州卷第18題同樣以作圖形式考查學生對圖形的變化規律的掌握情況；浙江杭州卷第8題則是通過在格點中刻畫旋轉后點的坐標來考查相關知識；湖北武漢卷第21題對學生要求較高，需要學生具備較強的分析問題的能力.

例5 （浙江·臺州卷）如圖6，△ABC的邊BC長為4 cm．將△ABC平移2 cm得到[△ABC，] 且[BB]⊥BC，則陰影部分的面積為? ? ? ? .

學業要求：知道平移的有關性質.

解法分析：陰影部分的面積等于四邊形BB′C′C的面積，此題答案為8 cm2．

試題分析：此題考查平移前后所得圖形的面積，比較簡明.

類題賞析：“圖形的變化”相關的度量考查在2022年中考試卷中涉及較少. 浙江嘉興卷第6題以中國古代婦女的發飾“方勝”為背景考查了平移中的距離計算，湖北十堰卷第15題則考查了扇形對稱變化后相關圖形的面積計算.

2. 聯系實際，考查應用，強化幾何直觀

“圖形的變化”相關試題往往和實際問題相結合，通過設置具體的問題情境，彰顯數形結合思想. 2022年全國各地區中考數學試卷中，很多試題都是借助現實情境考查學生對圖形的變化知識的掌握情況，只有少數地區使用數學情境考查該部分知識.

例6 （浙江·臺州卷）如圖7是戰機在空中展示的軸對稱隊形. 以飛機B，C所在直線為x軸、隊形的對稱軸為y軸，建立平面直角坐標系. 若飛機E的坐標為[40，a，] 則飛機D的坐標為（? ? ）.

（A）[40，-a] （B）[-40，a]

（C）[-40，-a] （D）[a，-40]

學業要求：理解幾何圖形的對稱性，感悟現實世界中的對稱美，知道可以用數學語言表達對稱.

解法分析：解決此題需要了解關于y軸對稱的點的坐標特點：縱坐標不變，橫坐標改變符號. 此題答案選B.

試題分析：此題借助問題情境給定對稱關系，考查用坐標語言表達對稱關系，設計新穎.

類題賞析：2022年中考新疆卷第3題考查的是關于x軸對稱的點的性質：橫坐標不變，縱坐標改變符號.

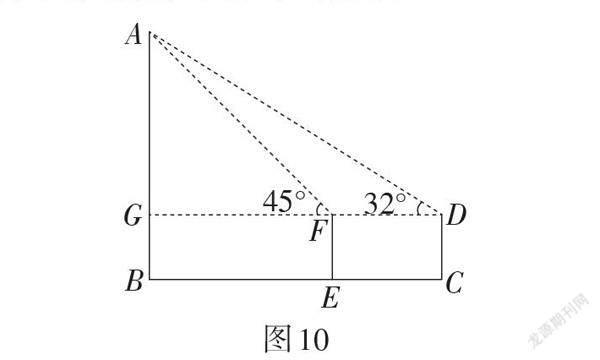
例7 （湖北·荊州卷）荊州城徽“金鳳騰飛”（如圖8）立于古城東門外. 如圖9，某校學生測量其高AB（含底座），先在點C處用測角儀測得其頂端A的仰角為32°，再由點C向城徽走6.6 m到點E處，測得頂端A的仰角為45°. 已知B，E，C三點在同一直線上，測角儀離地面的高度CD = EF = 1.5 m，求城徽的高AB.（參考數據：sin32°≈ 0.530，cos32°≈ 0.848，tan32°≈ 0.625.）

學業要求：能用銳角三角函數知識解決簡單的實際問題.

解法分析：如圖10，延長DF交AB于點G，則∠AGF = 90°，DF = CE = 6.6 m，CD = EF = BG = 1.5 m. 設FG = x m，先在Rt△AGF中利用銳角三角函數的定義表示出AG的長，再在Rt△AGD中，利用銳角三角函數的定義列出關于x的方程，進行計算即可解答.

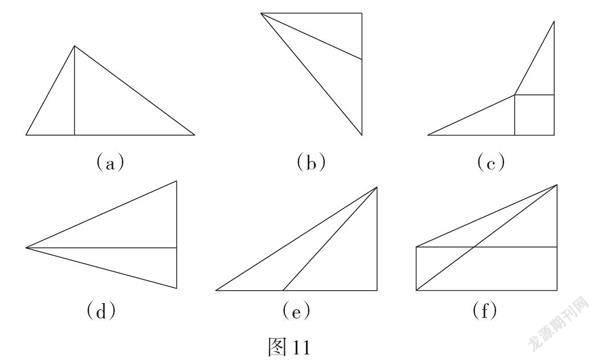
試題分析：此題立足人教版《義務教育教科書·數學》九年級下冊第81頁活動2中的基本圖形（其他版本的教材中也有體現），考查學生解直角三角形和解決實際問題的能力. 此題以測量無法直接測量的高度為背景，要求學生把實際問題轉化為數學問題，再運用所學的數學知識加以解決. 常見的借助銳角三角函數知識測量物體高度的基本圖形具有的重要特征為有一個公共元素，如圖11所示.

類題賞析：2022年中考天津卷第22題、湖南邵陽卷第25題、新疆卷第21題、四川遂寧卷第22題、河南卷第19題、四川眉山卷第22題、四川廣元卷第21題等同樣考查借助銳角三角函數知識測量物體高度解決問題；安徽卷第20題、重慶A卷第22題等考查利用上述基本圖形求航行距離.

3. 按圖索驥，探變求本，強化核心素養

例8 （四川·遂寧卷）如圖12，正方形ABCD與正方形BEFG有公共頂點B，連接EC，GA，交于點O，GA與BC交于點P，連接OD，OB，則下列結論一定正確的是（? ? ）.

① EC ⊥ AG ② △OBP ∽ △CAP

③ OB平分∠CBG ④ ∠AOD = 45°

（A）①③ （B）①②③

（C）②③ （D）①②④

學業要求：理解圖形的旋轉運動，知道圖形旋轉的基本特征，了解圖形相似的意義，會判斷簡單的相似三角形.

解法分析：由[BA=BC，BG=BE，∠ABG=90°+∠CBG=][∠CBE，] 易得[△ABG≌△CBE.] 所以[∠BAP=][∠OCP.] 所以[∠POC=∠PBA=90°，] 即①正確. 同時可得[A，B，C，][O]四點共圓，所以得[△OBP∽△CAP，] 即②正確. 且[∠AOD=∠ACD=45°，] 即④正確. 關于③，有[∠AOB=][∠ACB=∠BOE=45°，] 即[OB]平分[∠AOE.] 具體解題思維導圖如圖13所示. 此題答案選D.

試題分析：此題取材于經典的雙正方形旋轉構圖，通過旋轉構圖，設計一系列問題，考查學生對基本圖形旋轉的識別能力. 教材通過大量習題，呈現了兩個全等三角形或相似三角形通過旋轉產生的基本圖，旨在讓學生認識旋轉的性質，并運用這些性質分析、解決一些簡單的幾何問題.

常見的典型基本圖形的旋轉如圖14所示. 其中，相等的角常隱含在平行線、對頂角或某些角的和與差中.

類題賞析：2022年全國各地區中考數學試卷在選擇題和填空題中對旋轉變換的考查較多，天津卷第11題、湖南常德卷第7題、內蒙古包頭卷第11題、四川南充卷第16題、江蘇無錫卷第5題、浙江麗水卷第15題均以三角形旋轉為基本對象，考查探究過程中所產生的圖形的位置關系和數量關系等. 解決此類試題需要抽絲剝繭地挖出旋轉的基本圖形，然后結合等腰三角形、直角三角形、全等、相似等知識求解.

例9 （重慶B卷）在△ABC中，∠BAC = 90°，[AB=][AC=22，] D為BC的中點，E，F分別為AC，AD上任意一點，連接EF，將線段EF繞點E順時針旋轉90°得到線段EG，連接FG，AG.

（1）如圖15（a），點E與點C重合，且GF的延長線過點B，若點P為FG的中點，連接PD，求PD的長；

（2）如圖15（b），EF的延長線交AB于點M，點N在AC上，∠AGN = ∠AEG且GN = MF，求證：AM + [AF=2AE；]

（3）如圖15（c），F為線段AD上一動點，E為AC的中點，連接BE，H為直線BC上一動點，連接EH，將△BEH沿EH翻折至△ABC所在平面內，得到△B′EH，連接B′G，直接寫出線段B′G的長度的最小值.

學業要求：理解圖形旋轉的基本特征和性質.

解法分析：第（1）小題中，因為線段EF（即CF）順時針旋轉90°至EG，產生了等腰直角三角形EFG（即△CFG），點P為FG的中點，由等腰三角形“三線合一”性質，知EP ⊥ FG，所以△BPC是直角三角形，而D為其斜邊的中點. 由利用斜邊上的中線等于斜邊的一半，可得PD = 2.

第（2）小題中，如圖16，過點E作EH⊥AE交AD的延長線于點H，由已知可得△AEH為等腰三角形. 則容易證明△EFH ≌ △EGA. 所以∠EHF = ∠GAE = 45°. 所以∠GAE = ∠MAF. 由已知可知，∠AEG = ∠AMF = 90° - ∠AEM. 因為∠AGN = ∠AEG，所以∠AMF? = ∠AGN . 再結合GN = MF，可以證明△AMF ≌ △AGN. 所以AM = AG = FH. 所以[AM+AF=FH+AF=AH=2AE.] 結論得證.

第（3）小題，由于變化過程中點E的位置是確定的，所以線段BE的長為定值[10.] 所以點B′在以點E為圓心、[10]為半徑的圓上運動. 因為B′G + GE ≥ B′E，所以當EG最大，且B′，G，E三點共線時，B′G最小. 經驗證，當點F與點A或D重合時，EG取最大值，且這樣的點存在，進而可知線段B′G的最小值為[10-2.]

試題分析：此題先通過線段的旋轉變化產生兩個相似的等腰直角三角形，并以旋轉運動為出發點，設計一系列問題，層層遞進，著重考查學生在圖形變化的過程中捕捉不變規律的能力，并要求學生利用不變量進行邏輯推理，進而解決問題. 解決好此類問題的關鍵是要具備按圖索驥、通時達變的能力.

關于兩個等腰直角三角形的旋轉變化，建議掌握以下內容.

△ABC和△ADE是以點A為公共頂點的一組相似的等腰直角三角形.

（1）如圖17，則有：

① △ABD ≌ △ACE，且△ACE ∽ △ANM；

② 當點P，M，N分別是CD，DE，BC的中點時，△PMN也是等腰直角三角形.

（2）如圖18，點D在邊BC上，則有：

① △ABD ≌ △ACE；

② BC ⊥ CE.

（3）如圖19，記O，M，N分別是BE，AE，AB的中點，則有：

① 四邊形AMON是平行四邊形；

② △OCD是等腰直角三角形.

類題賞析：兩個相似圖形依據一定條件限制進行旋轉，產生的圖形性質頗多，以此為背景命題是近幾年中考的熱點. 2022年中考，四川成都卷第26題以兩個相似矩形旋轉為背景進行命題，江蘇連云港卷第27題以兩個直角三角板為背景進行圖形構造，都體現了這種命題思路.

例10 （安徽卷）已知四邊形ABCD中，BC = CD. 連接BD，過點C作BD的垂線交AB于點E，連接DE.

（1）如圖20（a），若[DE∥BC]，求證：四邊形BCDE是菱形.

（2）如圖20（b），連接AC，設BD，AC相交于點F，DE垂直平分線段AC.

① 求∠CED的大小；

② 若AF = AE，求證：BE = CF.

學業要求：理解軸對稱圖形的運動，知道軸對稱的基本特征，理解幾何圖形的對稱性.

解法分析：第（1）小題，根據題意，可知CE垂直平分BD，從而ED = EB. 進而可得∠EDB = ∠EBD. 再根據平行線的性質和角平分線的定義，可證明結論.

第（2）小題第①問，先根據垂直平分線的性質，得∠AED = ∠CED = ∠BEC. 再根據平角定義即可以得到∠CED = 60°；第②問中，利用“AAS”證明△ABF ≌ △ACE，得AC = AB. 所以AB - AE = AC - AF，即BE = CF.

試題分析：此題問題設計層次分明. 第（1）小題要求直接證明菱形，條件簡明. 第（2）小題設有兩個問，第①問主要借助垂直平分線和等腰三角形的性質進行角的傳遞，進而發現一個平角被三等分；第②問的設計對學生分析問題的能力提出了更高層次的要求，結論中隱含的特殊角、等腰三角形、四點共圓等為求解該題提供了豐富的想象空間. 此題由對稱基本圖形入手（試題涉及的部分基本圖形如圖21和圖22所示），衍生出一系列問題，題面簡潔，內涵深刻.

軸對稱是基本的圖形變換，是學習空間與圖形知識的必要基礎，常見的軸對稱圖形如圖23所示.

類題賞析：2022年中考湖南常德卷第26題以“風箏”形對稱圖形為背景進行相關知識的考查，很好地展示了探尋圖形的變化中不變的規律的過程. 四川成都卷第23題、四川德陽卷第16題、浙江臺州卷第16題、山東濱州卷第18題、浙江舟山卷第16題、江蘇揚州卷第17題、山東泰安卷第18題等則是通過選擇題或填空題考查對稱變換.

三、復習備考建議

通過對2022年全國部分地區中考數學試卷中的“圖形的變化”試題進行解題分析，提出以下備考建議.

1. 重視教材，回歸教材

課程標準是教材編寫的依據，也是中考命題的依據，教材是表達課程標準理念的有效載體. 通過分析發現，2022年中考“圖形的變化”試題考查問題的素材大多取材于教材. 因此，復習備考中，不能舍本逐末，要回歸教材、吃透教材，領會教材的編寫意圖. 要深度研究教材素材，創造性地分析、運用教材. 要對教材中的例題、習題，以及公式、定理進行深入拓展. 要跳出“題海”，多維度深挖教材，捕捉教材中的經典圖形，總結、提煉出軸對稱、旋轉等相關基本圖形，同時對衍生問題進行有效整合，以達到以不變應萬變的效果.

2. 關注基礎，強化理解

分析發現，要想解決好“圖形的變化”相關試題，需要厘清平移、軸對稱和旋轉三大變換的要素、性質，以及它們之間的聯系與區別；理解相似三角形的判定與性質、直角三角形的邊角關系；需要經歷從不同角度觀察立體圖形的過程，準確把握長方體、圓錐、球等簡單幾何體的側面展開圖. 在“圖形的變化”學習中，要重視基礎知識，要以信息技術演示或者實物操作的形式感悟圖形的軸對稱、旋轉、平移變化的基本特征，要理解感知變化是需要參照物的，要借助參照物闡釋圖形變化的基本特征，進而了解三類變化的基本性質.

3. 關注作圖，強化識圖

識圖能力是指學生在識圖過程中所表現出來的綜合素質. 會識別圖形指能在復雜交錯的圖形中尋找基本圖形，能將圖形進行分解、重組，從而發現有用的信息. 識圖能力直接關系到學生能否從問題中識別出基本圖形并加以運用，進而解決問題. 復習備考中，要通過作圖、用圖、識圖、構圖，掌握基本的作圖技巧，提升識圖能力和構圖水平，同時要加強圖形語言的表達能力. 問題解決中，要從觀察圖形特征入手，通過探尋、構造基本圖形，尋找解決問題的突破口.

“圖形的變化”專題備考中，要將圖形的變化和圖形的性質相結合，學會用數學的眼光觀察生活，用數學的語言描述生活，用數學的理性對待生活，最終形成學數學、用數學的意識和習慣.

4. 關注思維，強化推理

復習備考中，要重視學習的過程，主動經歷操作、觀察、猜想、歸納、驗證、證明、應用等學習環節，在發現問題、分析問題、解決問題的過程中感悟、體驗知識的再發現和再創造，實現“知其然，更知其所以然”，進而鍛造思維的嚴謹性，養成言必有據，分析細致、縝密的習慣. 在學習圖形的變化內容時，若要解決旋轉問題，則要學會從“新圖形自身的性質有哪些變化？”“對應元素之間有何數量和位置關系？”“新圖形又生成了哪些新條件或新規律？”“題干的條件和新發現的結論都得到有效使用了嗎？”四個方面分析問題. 總之，要通過經歷知識的形成過程發展思維的深度和廣度，進而提高思維的靈活性、發散性和創造性.

四、典型模擬題

1. 如圖24，在Rt△ABC中，[∠ACB=90°，BC=][2AC，] 點[D，E]分別是邊[BA，BC]的中點，連接[DE．] 將△BDE繞點B順時針旋轉[α 0°<α<90°，] 得到△BFG，點D的對應點是點F，連接AF，CG．

（1）求證：[∠BFA=∠BGC；]

（2）若[∠BFA=90°，] 求[sin∠CBF]的值．

答案：（1）略.

（2）[sin∠CBF=215+510．]

【評析】此題以兩個相似的特殊直角三角形旋轉所得的圖形作為考查對象. 第（1）小題要求證明這個圖形的一般性質；第（2）小題在第（1）小題的基礎上研究特殊情形. 解題過程中多次運用圖形變化的性質，需要進行適當的計算.

2. 如圖25，矩形[ABCD]中，[AB=12，AD=25，] 點[E]是邊[BC]上一點，[CE=16，] 點[M]是邊[AD]上一動點，點[N]是邊[BC]上一動點，射線[AN]與射線[ME]相交于點[F]，且滿足[∠AFM=∠EAD，] 將[△ABE]沿[AB]翻折得到[△ABG].

（1）連接[DE]，求[∠AED]的度數；

（2）當[△AFM]是以[FM]為腰的等腰三角形時，求[EN]的值；

（3）當[AN]平分[∠EAD]時，求證：[GF]平分[∠AGE.]

答案：（1）[∠AED=90°]；

（2）[0]或3；

（3）略.

【評析】此題考查對稱變換的相關知識，以矩形為基本圖形，通過變化考查相關角度的關系，以及全等與相似的應用. 第（3）小題多次運用相關條件得到相等的角或線段，最終利用全等得到欲證結論，對學生的識圖能力和邏輯推理能力要求較高.

參考文獻：

［1］中華人民共和國教育部. 義務教育數學課程標準（2022年版）［M］. 北京：北京師范大學出版社，2022.

［2］劉金英，顧洪敏. 靜觀其變? 順勢而為：2019年中考“圖形的變化”專題命題分析［J］. 中國數學教育（初中版），2020（1 / 2）：89-96.

［3］鐘文麗，萬妍青. 以“作圖”促理解? 探“變化”提素養：2020年中考“圖形的變化”專題解題分析［J］. 中國數學教育（初中版），2021（1 / 2）：84-90.

［4］趙軍才，薛紅霞. 圖亦可料? 變守其本：2021年中考“圖形的變化”專題命題分析［J］. 中國數學教育（初中版），2022（1 / 2）：84-90.

［5］陳耀忠. 基于核心素養的試題研究：以雙等腰直角三角形旋轉圖形為例［J］. 中國數學教育（初中版），2017（7 / 8）：21-25.

基金項目：蚌埠市教育科學規劃課題——安徽省中考數學試卷與課標一致性研究（2021073）.

作者簡介：陳耀忠（1970— ），男，正高級教師，主要從事中學數學教學、競賽和中高考命題研究；

孫陳威（1987— ），男，一級教師，主要從事中考數學試題與課標一致性研究.