四旋翼無人機參數預測和抗擾動自適應軌跡跟蹤控制

司 勇， 王兆魁， 李東方， 吳 奇

(1.清華大學 航天航空學院，北京 100084； 2.福州大學 電氣工程與自動化學院，福建 福州 350108；3.上海交通大學 電子信息與電氣工程學院，上海 200230)

四旋翼無人機是一種通過遙控或機載程序實現飛行任務的無人駕駛設備。這種無人機憑借機動靈活、成本低和結構簡單等優點在電力巡檢、農業植保和環境監測等領域被廣泛使用[1]。因此，四旋翼無人機的研究受到廣大研究學者們的青睞[2-3]。

當前，四旋翼無人機的研究高度發展，研究學者們取得了頗豐的成果[4]。比較有代表性的有Draganflyer Innovation公司研發的Draganflyer系列四旋翼無人機飛行器，這種無人機在軍事偵察、地質災害測繪等領域發揮著重要作用[5-6]，操作人員可遠程遙控飛行器的運動方向和速度來完成指定任務。洛桑聯邦理工學院研發了兩代小型四旋翼無人機 OS4和OS4Ⅱ，設計了完全自主的無人機控制系統，賦予了無人機在室內的懸停功能，提高了無人機的自主避障能力[7-10]。Kumar等研究了四旋翼無人機的編隊協同控制，這使得無人機群編隊在特定場景中能夠完成搜索和救援任務[11-13]。

由于四旋翼無人機在飛行過程中會受到紊流風場的影響，這給無人機的軌跡跟蹤運動帶來了極大的挑戰[14]。Chen等[15]使用PID神經網絡控制算法設計了四旋翼無人機的軌跡跟蹤控制器，這種控制器沒有考慮風場擾動對無人機路徑跟蹤的影響。一旦風力擾動過大，無人機就會偏離約定軌跡。為了提高四旋翼無人機在紊流風場擾動下的軌跡跟蹤穩定性，Moreno-Valenzuela等[16]提出了一種基于分布式 PID 神經網絡的無人機路徑跟蹤控制方法，該方法采用雙閉環控制方案，在一定程度上提高了無人機的軌跡跟蹤穩定性等。為了提高無人機路徑跟蹤的收斂速度，Mian等[17]將反步法應用在四旋翼無人機上并取得良好的效果[17]。此外，Chen等[18]將反步控制與滑模控制相結合，設計了一種具有魯棒性的四旋翼無人機位置和偏航角控制的反步滑模控制器。該控制器使用了虛擬控制輸入，設計了系統故障的估計值，保證了飛行器的軌跡跟蹤性能。為了提高四旋翼無人機的軌跡跟蹤精度，Allahverdy等[19]將迭代學習控制應用于無人機的路徑跟蹤控制中，提出了基于迭代學習控制的反步積分滑模控制方法，該方法有效提高了系統的控制精度和誤差的魯棒性。

針對四旋翼無人機模型的非線性特點，Raffo等[20-21]設計了無人機跟蹤位置誤差的積分預測控制器，這種控制器能夠使無人機在受到持續外界干擾時仍然可以跟蹤參考路徑。但是，由于積分作用緩慢，無人機在高速風場擾動情況下的跟蹤效果并不理想。為了解決這個問題，Yao等[22]提出了基于擴展狀態觀測器的四旋翼無人機積分滑模控制器，該控制器利用擴展狀態觀測器對風場的擾動變量進行估計，并用估計值來補償自適應積分滑模面，有效提高了無人機的跟蹤效率。類似地，Shao等[23]設計了基于擴展狀態觀測器的四旋翼無人機積分反步滑模的控制器，提高了無人機的抗擾動能力，保證了無人機系統在參數不確定情況下的軌跡跟蹤精度。為了提高四旋翼無人機在軌跡跟蹤過程中的自適應能力，Modid等[24]將自適應方法應用到滑模控制中，研究了無人機系統在參數不確定情況下的整定問題，證明了無人機系統的未知參數在任何時刻都可以實現收斂與穩定。

盡管研究學者們在四旋翼無人機的軌跡跟蹤控制研究中取得了許多重要成果，但是還存在一些亟需解決的問題。例如，四旋翼無人機的姿態和位置的高耦合性會導致無人機自主化水平低的問題；無人機在飛行控制中受氣流、風阻和執行器故障等外界環境的擾動會導致軌跡偏離的現象；控制系統的自適應能力研究不完善會導致無人機飛行效率低、抖振嚴重和穩定性不足的問題[25-26]。

為了提高四旋翼無人機的軌跡跟蹤精度，抵消飛行過程中的干擾波動，增加控制系統的自適應性和穩定性，筆者提出一種基于滑模控制的四旋翼無人機參數預測和抗擾動的自適應軌跡跟蹤控制器。所提出的控制器通過對四旋翼無人機系統的不確定狀態參數進行預測，提前對無人機給予自適應補償，有效提高了無人機的軌跡跟蹤效率和跟蹤精度，確保了自適應軌跡跟蹤控制器的穩定性；通過預測四旋翼無人機所受的外界擾動，提前對系統的控制輸入進行干擾補償，降低了氣流、風阻和執行器故障等外界環境對無人機軌跡跟蹤控制的消極影響，提高了無人機的抗擾動能力，消除了無人機在飛行過程中的抖振現象，從而提高了系統對環境的自適應適應力。通過實驗，比較了四旋翼無人機在不同控制器作用下的軌跡跟蹤性能曲線，驗證了所提出的控制器能夠消除四旋翼無人機的姿態角誤差的超調現象，減小位置誤差的波動峰值和頻率，有效提高了無人機飛行速度的穩定時間和跟蹤誤差的收斂穩定性。

1 模型

四旋翼無人機是一種典型的欠驅動六自由度系統。這種無人機由4個獨立的電機和4個螺旋槳組成。通過調節四旋翼無人機的4個電機的轉速，螺旋槳產生的升力會隨之改變，以此實現無人機的飛行姿態轉換。由于四旋翼無人機使用反對稱結構的設計理念，因此無人機相鄰的2個螺旋槳始終保持反方向旋轉[27]。

四旋翼無人機的建模使用2套獨立的空間坐標系，分別為慣性坐標系OXYZ和無人機坐標系Bxyz。無人機在OXYZ坐標系下的位置為[x,y,z]T，翻滾角為φ，俯仰角為θ，偏航角為ψ，如圖1所示。四旋翼無人機系統的4個控制輸入為ui(i=1,…，4)。其中，u1控制無人機的垂直起降運動，u2控制無人機的翻滾運動，u3控制無人機的俯仰運動，u4控制無人機的偏航運動。系統包括6個輸出，分別是沿3個坐標軸的平移運動(垂直運動、前后運動、側向運動)以及圍繞3個坐標軸的旋轉運動(翻滾運動、俯仰運動、偏航運動)。Ωi為第i(i=1,…,4)個電機的轉速。參考文獻[18]，得到四旋翼無人機的非線性力學模型，如式1所示。

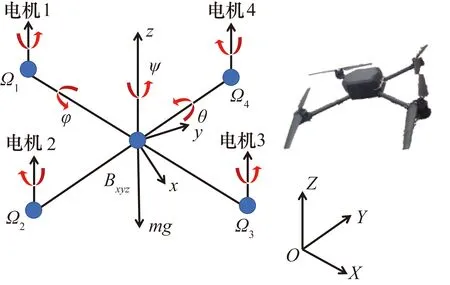
圖1 四旋翼無人機模型

(1)

式中：kφ、kθ和kψ分別為四旋翼無人機在3個轉動方向上的氣動阻力系數；kx、ky和kz分別為無人機在3個坐標方向上的空氣阻力系數；Ir=Ω1-Ω2+Ω3-Ω4為螺旋槳角速度的綜合殘差；Ix、Iy和Iz分別為四旋翼無人機圍繞機體坐標系的轉動慣量；l為無人機旋翼中心至機體坐標系原點的距離。

為簡化四旋翼無人機的模型參數，設

設計無人機在x、y、z方向上的虛擬控制輸入為

(2)

由于欠驅動的四旋翼無人機存在非線性項和耦合項，因此四旋翼無人機系統在本質上是一個不穩定系統。無人機在軌跡跟蹤的過程中不僅受到建模不確定性影響，而且受到外界風擾和故障等影響。因此，研究四旋翼無人機在受到外部干擾以及故障影響下的軌跡跟蹤方法具有重要意義。

為了抵消四旋翼無人機在軌跡跟蹤過程中受到的干擾和故障，需要將外界干擾和偏差故障統一成系統的擾動項，并在控制器中引入擾動補償項，通過自適應估計方法來確保控制器的穩定性[28]。設置fi(i=1,2,3)為四旋翼無人機在轉動角度上所受的故障項。σi(i=1,2,3)為無人機在轉動角度上所受的擾動項。四旋翼無人機的轉動角度故障項和擾動項之和為biΔi=fi+σi(i=1,2,3)。設置hi(i=1,2,3)為四旋翼無人機在運動位置方向上所受的故障項，δi(i=1,2,3)為無人機在運動位置方向上所受的擾動項，則無人機的運動位置故障項和擾動項之和為Δi=hi+δi(i=4,5,6)。因此，考慮擾動以及執行器偏差故障的無人機控制模型為

(3)

式中：vφ為滾轉角速度；vθ為俯仰角速度；vψ為偏航角速度；vx為切向運動速度；vy為法向運動速度；vz為垂向運動速度。

2 目標

四旋翼無人機在軌跡跟蹤的過程中，需要完成兩項控制目標，分別是姿態角目標和飛行位置目標[29]。四旋翼無人機的姿態角目標和飛行位置目標之間存在相互作用和相互聯系。其中，姿態角目標的實現可以使無人機的翻滾角、俯仰角和偏航角誤差收斂且穩定；飛行位置目標的實現可以使無人機的切向、法向和垂向位置誤差收斂且穩定[30-31]。由于四旋翼無人機的姿態和位置之間具有高度的耦合性，因此，姿態角的穩定性會影響無人機的飛行位置軌跡，飛行位置的收斂速度會反作用姿態角的轉動角度。只有同時完成自適應軌跡跟蹤控制器的兩項目標才能使無人機快速和準確地跟蹤期望軌跡。

2.1 姿態角目標

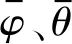
(4)

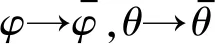
2.2 飛行位置目標

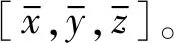
(5)

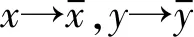
3 控制器設計

為了實現制定的控制目標，需要利用滑模控制方法和自適應控制方法對四旋翼無人機的姿態角子系統和位置子系統分別設計[32]。

3.1 姿態角子系統

(6)

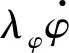
對四旋翼無人機的翻滾角誤差，俯仰角誤差和偏航角誤差進行為微分:

(7)

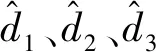
根據自適應控制方法設計系統的控制輸入u2，u3和u4:

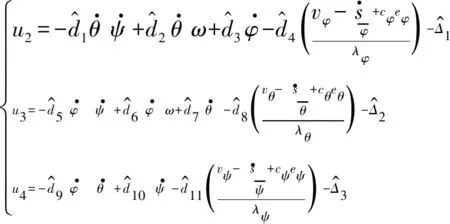
(8)

式中:cφ>0，cθ>0和cψ>0為正常數增益。

設計Lyapunov候選函數L1、L2和L3：

(9)

式中：γi>0(i=1,…,11)為正常數增益；β1，β2和β3為正常數增益。

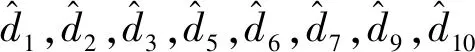
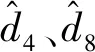
(10)

對L1、L2和L3進行微分可以得到：

(11)

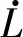
考慮具有外部擾動的四旋翼無人機的姿態子系統所設計的控制輸入(式(8))能夠保證無人機姿態子系統在擾動發生的情況下保持穩定，故四旋翼無人機系統的姿態角度誤差eφ、eθ和eψ可以收斂且穩定。

3.2 位置子系統

(12)

設置虛擬控制項為

(13)

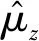
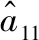
(14)

式中：η1>0，η2>0和η3>0為正常數增益。

設置系統的控制輸入u1為

(15)

式中：cz>0為正常數增益。

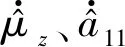
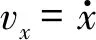
(16)

設置虛擬控制項為

(17)

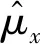
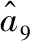
(18)

式中：η4>0，η5>0，η6>0，η7>0，η8>0和η9>0為正常數增益。

設置系統的位置控制輸入ux和uy為

(19)

式中：cx>0和cy>0為正常數增益。

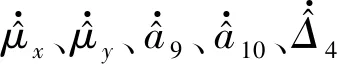
設四旋翼無人機的位置誤差的Lyapunov函數為

(20)

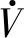
(21)

(22)

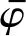
4 仿真

下面通過仿真實驗來驗證所提出的控制器可以使四旋翼無人機快速并準確的跟蹤期望路徑。在仿真實驗中，系統的初始參數如表1所示。

四旋翼無人機跟蹤的期望軌跡如式(23)所示，無人機的姿態子系統的擾動變量如式(24)所示，位置子系統的擾動變量如式(25)所示。通過分析無人機在本文所提出控制器(簡稱PC)、文獻[18]提出的反步滑模控制器(Backstepping Sliding Mode Controller,BSMC)、標準反步控制器(Standard Backstepping Controller,SBC)和文獻[24]提出的自適應滑模控制器

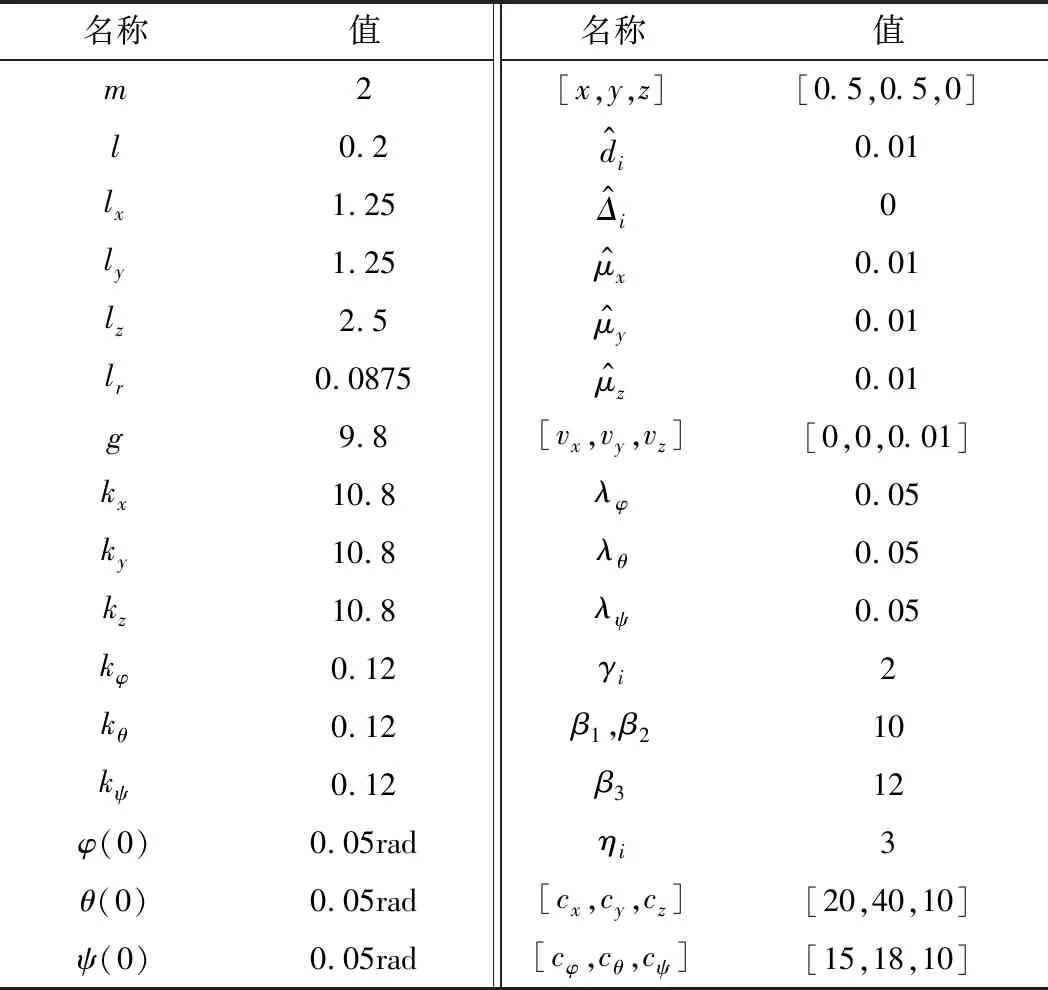
表1 參數設置

(Adaptive Sliding Mode Controller,ASMC)下的跟蹤性能曲線，驗證所提出的控制器的有效性和優越性。

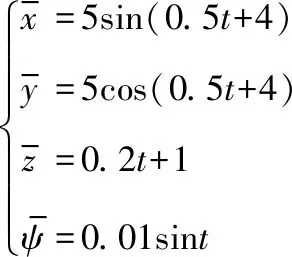
(23)

Δ1=Δ2=Δ3=cos(0.5t+0.1)

(24)

Δ4=Δ5=Δ6=sin(t+0.1)

(25)

四旋翼無人機在4種不同控制器作用下的飛行軌跡如圖2所示。無人機在SBC下的運動軌跡與參考軌跡在起始階段偏離最大。無人機在BSMC、ASMC和PC下的飛行軌跡都可以快速跟蹤到理想路徑。但是，相比之下，PC的作用可以使四旋翼無人機最快、最穩定地跟蹤參考軌跡。

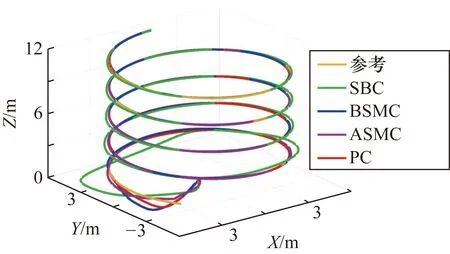
圖2 無人機飛行軌跡

四旋翼無人機在4種控制器作用下的飛行軌跡如圖3所示。將無人機的飛行軌跡與參考路徑作差，得到無人機的飛行位置誤差如圖4所示。無人機在BSMC、ASMC和PC作用下的切向和法向飛行軌跡可以跟蹤到期望路徑。在PC作用下的切向和法向位置誤差可以迅速收斂。在BSMC、ASMC和PC作用下，無人機的切向位置誤差的收斂時間分別是4 s、4 s和1 s，法向位置誤差的收斂時間分別是4 s、6 s和1 s。在ASMC和PC作用下的垂向位置誤差可以無超調的快速收斂到穩定狀態。綜上所述，通過對比四旋翼無人機在不同控制器作用下的飛行位置特性，體現出了PC的優越性和有效性。

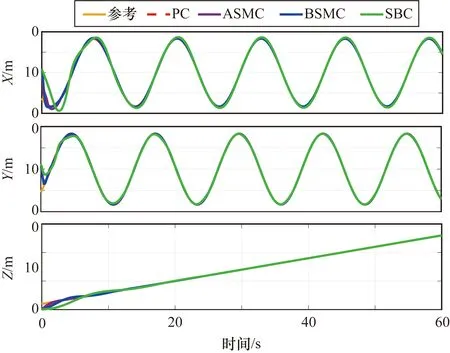
圖3 無人機飛行軌跡分量

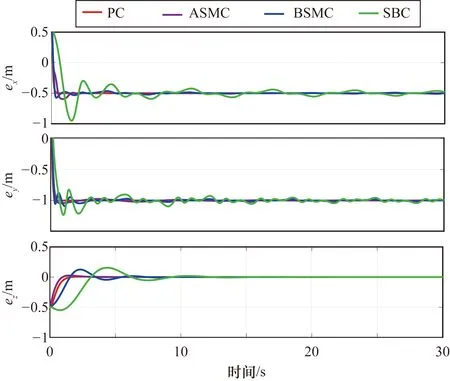
圖4 無人機飛行位置誤差

四旋翼無人機的飛行速度誤差如圖5所示。可以看出，無人機在PC作用下的切向和法向速度誤差可以在1s內快速收斂，并且收斂后的誤差曲線具有極高的穩定性和平滑性。此外，四旋翼無人機在BSMC、SBC、ASMC和PC作用下的垂向速度誤差在穩定前分別經過的超調次數為2次、2次、1次和1次，誤差的收斂時間分別是14 s、14 s、4 s和2 s。因此，四旋翼無人機在PC的控制下的飛行速度誤差不僅收斂快、穩定性好，而且收斂后的誤差曲線平滑。

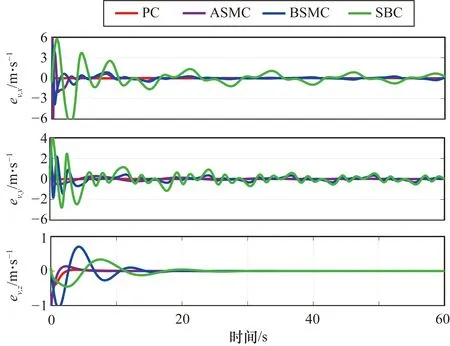
圖5 無人機飛行速度誤差分量

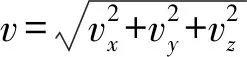
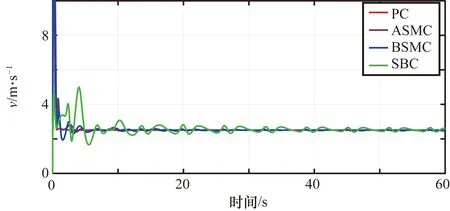
圖6 無人機飛行速度

將無人機的飛行姿態角與參考姿態角作差，得到無人機的飛行姿態角誤差，如圖7所示。相比之下，四旋翼無人機在PC下的翻滾角和俯仰角誤差在初始階段雖然出現一定的抖動現象，但是抖動幅值小、穩定性好。此外，雖然四旋翼無人機在不同控制器作用下的偏航角誤差都實現了穩定，但是，無人機在PC下的偏航角誤差曲線在穩定前的擺動幅值小，收斂速度快，收斂后的誤差曲線穩定性好。綜上所述，四旋翼無人機的飛行姿態角特性曲線可以很好地體現出PC的優越性。

四旋翼無人機的飛行姿態角速度誤差如圖8所示。可以看出，無人機在BSMC和SBC作用下的翻滾角和俯仰角速度誤差存在抖動幅度大、抖動頻繁、收斂速度慢的不足。相比之下，無人機在ASMC和PC作用下的翻滾角和俯仰角速度誤差曲線具有抖動頻率小、抖動幅值小、收斂速度快和誤差穩定性好的優點。在PC作用下，無人機的誤差曲線整體波動小、抖動頻率低、收斂速度快且平滑、姿態轉動平滑，這大幅提高了無人機的軌跡跟蹤穩定性。

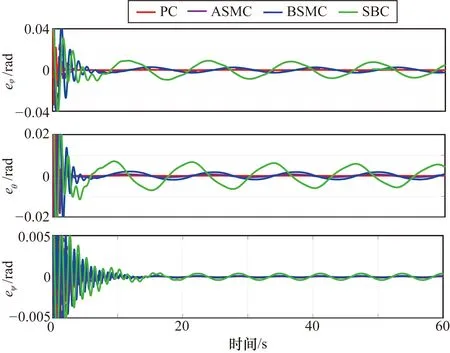
圖7 無人機飛行姿態角誤差

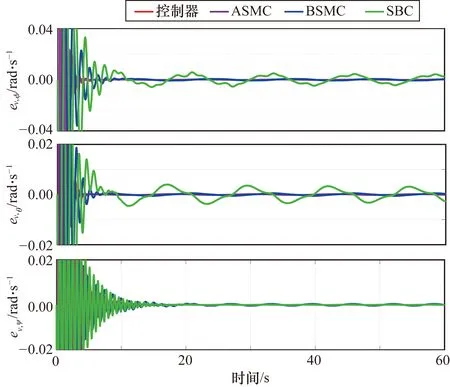
圖8 無人機飛行姿態角速度誤差

無人機的系統控制輸入曲線如圖9所示。無人機在起飛時，垂直起降輸入變化大，這使無人機可以快速跟蹤參考軌跡。在PC的作用下，無人機快速跟蹤到期望路徑后，飛行位置誤差和姿態角誤差實現了收斂，無人機實現了穩定的軌跡跟蹤運動，無人機的垂直起降輸入也實現了穩定。受無人機初始作用的影響，無人機的偏航輸入在8 s內振動劇烈，因為無人機在初始軌跡跟蹤的過程中不僅要改變高度，而且要改變偏航位置。相比之下，無人機的翻滾輸入和俯仰輸入僅在3 s內發生大幅變化。當無人機跟蹤到參考軌跡后，無人機的翻滾、俯仰和偏航輸入呈現出規律的正弦波形式。

四旋翼無人機系統的參數變量預測值和虛擬控制函數的參數變量預測值變化曲線如圖10和圖11所示。在PC控制下，預測值曲線可以快速穩定，并且穩定后的曲線整齊無毛刺。

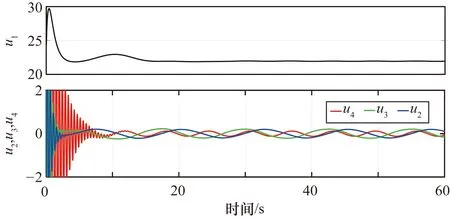
圖9 控制輸入

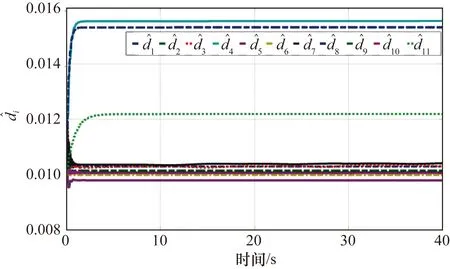
圖10 系統的參數變量預測值

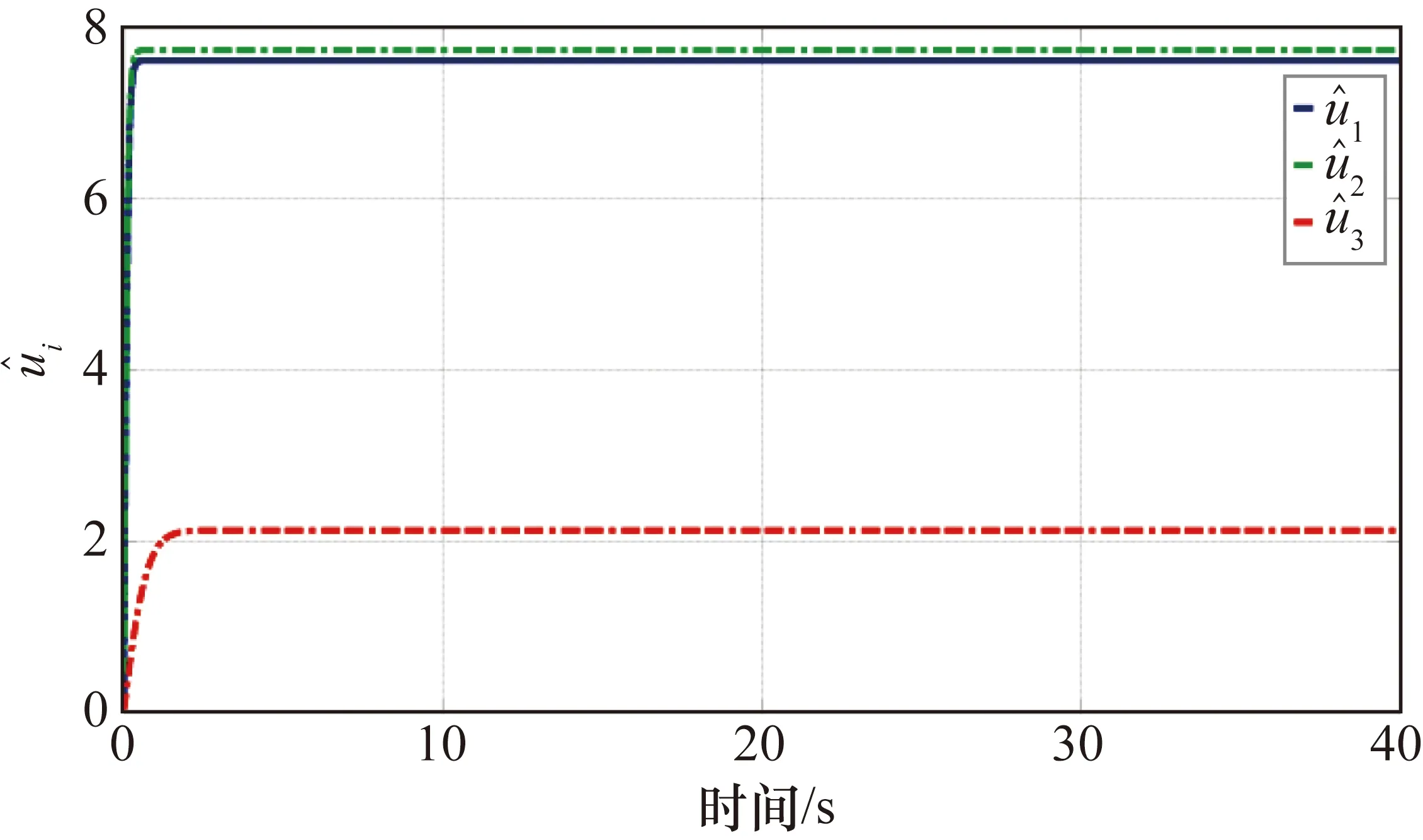
圖11 虛擬控制函數的參數變量預測值

四旋翼無人機系統的姿態和位置擾動變量預測值變化曲線如圖12和圖13所示。由于初始擾動變量為正弦曲線，因此，在PC的作用下，無人機的擾動變量預測值為穩定的正弦波動形式。

綜上所述，PC不僅有效提高了四旋翼無人機的軌跡跟蹤效率，加快了跟蹤性能誤差的收斂速度，而且減小了跟蹤誤差的波動峰值，提高了系統的穩定性。通過仿真實驗，所提出的基于滑模控制的四旋翼無人機參數預測和抗干擾的自適應軌跡跟蹤控制器的有效性和優越性被驗證。

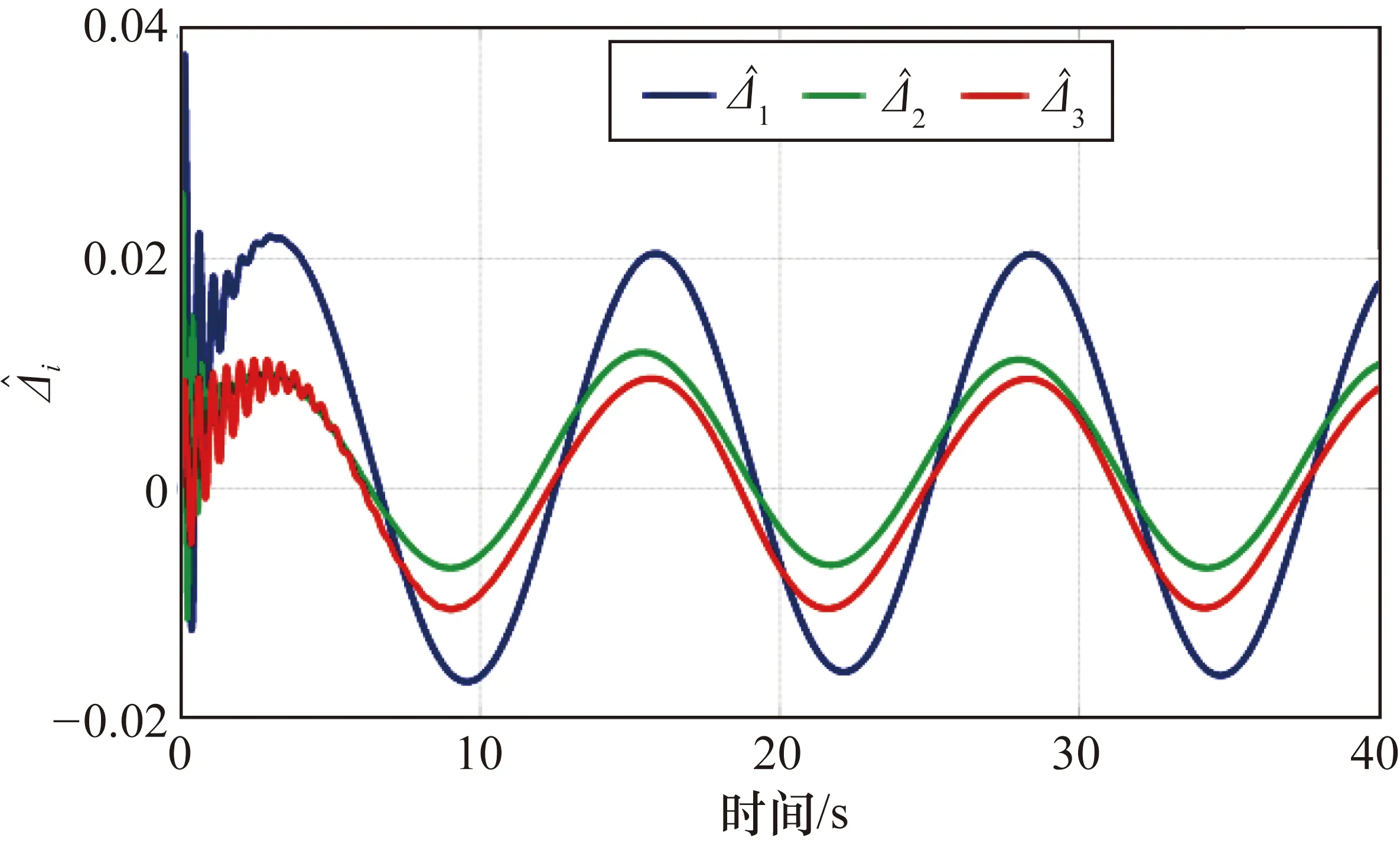
圖12 姿態擾動變量預測值

5 結束語

本文提出了一種基于滑模控制的四旋翼無人機參數預測和抗干擾的自適應軌跡跟蹤控制器。定義了四旋翼無人機具有外部擾動的非線性力學模型，探討了無人機軌跡跟蹤的姿態角目標和飛行位置目標，通過預測系統的不確定狀態參數和無人機所受的外界擾動，設計系統的姿態控制輸入和位置控制輸入，實現了無人機的自適應軌跡跟蹤控制。