基于振動可視化的電力變壓器ODS測量方法研究

彭 鵬， 邵宇鷹， 馬 魯， 孫 寧， 韓 靜

(國網上海市電力公司，上海 200122)

電力變壓器的振動狀態反映了其工作運行的狀態。通過對變壓器的振動進行測量與分析，可以判斷其運行是否正常，以及是否存在故障。依靠傳感器來獲取振動信號是目前主要的針對電力變壓器的振動狀態檢測方法[1-4]。但此種接觸式測量方法會對振動的檢測產生諸多影響，例如負載效應、測量過程復雜、誤差較大等[5]。而視覺測量作為一種非接觸測量技術，能夠有效避免上述問題的發生并且可得到可靠的結果。

自20世紀80年代以來，視覺測量技術一直都是非常熱門的研究領域，并經歷了從實驗室走向實際應用的發展階段。作為一種先進的測量技術，視覺檢測技術己經在工業產品檢測、結構狀態監測、人體運動分析和極端環境下的測量中得到了廣泛的應用[6]。Wahbeh等[7]實現了對基礎設施系統(如大跨度橋梁)在多個位置上的測量研究與試驗，得到了位移歷史和其復雜的三維變形。Yang等[8]結合了多尺度金字塔分解表示方法和無監督學習盲源分離(Blind Source Separation,BBS)技術，以相對高效和自主的方式實現了對結構架的高分辨率模式形狀等信息的視頻測量提取。Huang等[9]提出了基于計算機視覺的典型氣動彈性高層建筑模型風洞試驗振動測量方法，開發了模板角算法用于目標跟蹤。Son等[10]提出了圓柱結構振動位移的視覺遠程測量方法，并給出了測量振動位移數據誤差的估計方法。徐秀秀等[11]針對柔性結構振動測量研究的需要,設計了一種基于機器視覺的非接觸式柔性臂振動測量系統。閆志敏等[12]采用機器視覺技術，對水潤滑橡膠艉軸承的振動進行了測量分析。還有許多學者針對柔性結構進行了機器視覺測量的研究[13-15]。雖然國內外學者利用該技術滿足了多種情況下的測量需求，但在電力行業的應用甚少。

本文針對電力變壓器的振動測量需求，提出了一種基于振動可視化技術的工作振型(Operational Deflection Shape，ODS)測量方法，并通過實驗對比與應用研究驗證了方法的可行性。其主要實現途徑是基于稠密光流法進行運動捕捉，得到振動的位移量，從而形成變壓器運行時的ODS。本方法的提出為視覺測量技術在工程中的應用推廣提供了參考，且ODS分析有助于可視化部分振動故障并改進設備狀態分析方法。

1 理論介紹

1.1 電力變壓器振動原理

電力變壓器的振動主要由變壓器本體結構(鐵芯、繞組等的統稱)的振動、有載調壓分接開關切換時的瞬態振動和冷卻裝置工作時的振動幾部分構成。在小于100 Hz的頻率范圍內，主要是由冷卻系統引起的基本振動；在進行有載調壓分接開關的切換操作時，會產生瞬態振動，其頻率成分的構成均為kHz量級，屬于高頻振動；而繞組和鐵芯等構成的本體結構的振動屬于變壓器穩態運行時的振動，以100 Hz為基頻，伴有其他高次諧波分量。本文主要研究電力變壓器本體結構的振動。

變壓器繞組的振動主要是由設備運行中電流流經繞組在其周圍產生的漏磁場所產生。在繞組電流和漏磁場的共同作用下，繞組內部將產生電動力，并隨著負載電流的增大而增大。繞組中電動力Fw與負載電流I的平方成正比，即Fw∝I2。因此油箱表面可以檢測到的振動信號幅值與負載電流的平方成正比，頻率為電流頻率的2倍，即100 Hz。

電力變壓器鐵芯的振動主要由2個部分構成:① 硅鋼片的磁致伸縮引起的鐵芯振動;② 硅鋼片接縫處和疊片之間因漏磁而產生的電磁吸引力引起的振動。近年來，鐵芯疊積和綁扎方式的改進使電力變壓器的額定工作磁密足夠小，因此硅鋼片磁致伸縮引起的鐵芯振動遠大于硅鋼片間的電磁吸引力所引起的振動，或負載電流產生的漏磁引起的線圈振動。在鐵芯壓緊力足夠大時可認為鐵芯的振動主要取決于硅鋼片的磁致伸縮。鐵芯所受電磁力Fc與變壓器電源電壓U的平方成正比，即Fc∝U2。根據磁致伸縮的原理，鐵芯硅鋼片磁致伸縮的頻率應為交流電頻率的2倍，對于電力變壓器，鐵芯振動的基頻即磁致伸縮的頻率為工頻的2倍，即100 Hz。

綜上所述，空載下電力變壓器油箱表面振動信號可以反映出變壓器的運行狀態，而其振動特性與繞組和鐵芯的工作狀態息息相關。因此通過研究變壓器的振動狀態，可以診斷出變壓器的狀態。

1.2 ODS分析

ODS[16-17]是振動狀態分析技術之一，不同于模態變形分析，其變形形狀是各階模態振型的線性疊加。

振動測試時，通常是測量結構在某種工作狀態下的響應。此時，處于工作狀態下的結構受到工作載荷或環境載荷的激勵，通過各種傳遞路徑，在測量位置產生相應的振動響應。受到工作載荷或環境載荷的激勵后，結構會被激起一部分模態，激勵起來的每一階模態都會在測量位置處產生相應的響應。這些激勵起來的模態在測量位置的響應的疊加，即振動測量得到的響應。

當前測量獲得的響應是結構受工作載荷或環境載荷的激勵所激起來的所有模態在這個測量位置處產生的響應的疊加，即系統各個測點的響應是被激勵的模態向量φ與模態坐標q的乘積。其中，φ為模態振型;q為加權系數，表示各階模態對總響應的貢獻量。

ODS分析是測量處于工作狀態下的變壓器振動響應，再直接使用響應來顯示其ODS。由于響應數據可以是時域或頻域的，因而ODS可分為時域ODS和頻域ODS。時域ODS為所有模態在當前這一時刻的疊加，頻域ODS為所有模態在當前頻率處的疊加。

1.3 光流法

目前的視覺測量技術主要有幀間差分法、背景差分法和光流法等。光流法因具有相對較強的抗干擾能力和較高的識別準確率而被廣泛關注。

光流(Optical Flow)是空間運動物體在觀察成像平面上的像素運動的瞬時速度。光流法是利用圖像序列中像素在時間域上的變化以及相鄰幀之間的相關性來找到上一幀與當前幀之間存在的對應關系，從而計算出相鄰幀之間物體的運動信息的方法。光流法主要可以分為2類：以LK(Lucas-Kanade)[18]光流法為代表的稀疏光流法和以HS(Horn-Schunck)[19]光流法為代表的稠密光流法。由于LK光流法中只對特征點進行追蹤，會丟掉圖像中大量的有用信息，容易導致特征不足，因此本文選取稠密光流法作為振動可視化測量的圖像處理方法。

稠密光流法是一種針對圖像進行逐點匹配的圖像配準方法。不同于稀疏光流法只針對圖像上若干個特征點，稠密光流法計算圖像上所有點的偏移量，從而形成一個稠密的光流場。通過這個稠密的光流場，可以進行像素級別的圖像配準，所以其配準后的效果也明顯優于稀疏光流法配準的效果。

光流法的基本約束條件為運動物體的灰度在很短的時間間隔內保持不變，因此設立約束方程式為

(1)

式中：u和v分別為像素在x軸和y軸上的運動速度；Ix和Iy為圖像在x方向和y方向的梯度；It為圖像灰度對時間的變化量。

稠密光流法中的Horn-Schunck算法在光流基本約束方程的基礎上附加了全局平滑假設，假設在整個圖像上光流的變化是光滑的，即物體運動矢量是平滑的或只是緩慢變化的。引入速度平滑項為

(2)

根據2個約束條件，可以建立極小化方程,求解最小值為

(3)

式中：α為平滑權重系數，表示速度光滑項所占的權重。并利用高斯-賽德爾迭代法進行求解，得到圖像第(n+1)次迭代估計(un+1,vn+1)，其中u和v的均值采用九點差分格式進行計算。

(4)

與第n次迭代結果相比，當誤差小于預先設定的值時，迭代結束，得到了光流向量 [u,v]。

為了更好地可視化，可用顏色編碼結果，振幅大小對應于圖像的色調值，得到表征振動量的云圖。

2 振動可視化測量實驗

2.1 實驗設計

為驗證筆者提出的基于振動可視化的ODS測量方法的可行性，本文先對簡單結構懸臂梁進行實驗測試。具體實驗流程設計如圖1所示。

圖1 變壓器振動ODS測量實驗流程設計

首先，將懸臂梁的固定端設于激振器上，在激振器的作用下懸臂梁發生振動。由高速攝像機拍攝振動狀態下的懸臂梁，攝影燈起補光作用，所攝高幀頻視頻儲存于存儲卡中，通過前文所述的稠密光流法進行處理后，得到被測梁的ODS。

為檢驗通過振動可視化方法所得振動數據的有效性，設計了振動測試實驗的參考組。按照傳統振動測量方法，在懸臂梁上安裝數枚加速度傳感器，采集振動信號，并通過后續數據處理形成被測梁的ODS，以此作為參照進行振動可視化方法的驗證。

2.2 實驗臺搭建

根據上述實驗設計流程，在實驗室內搭建了懸臂梁振動ODS測量實驗臺，其主要設備構成如圖2所示。

1—激振器；2—待測懸臂梁；3、4—攝影燈；5—數據采集設備；6—功率放大器；7—高速攝像機； 8—電源。

本實驗臺搭建所用懸臂梁長30 cm、截面積1 cm×1.5 cm，在梁上等距選取5個點作為傳感器安裝點，從梁的固定端至自由端依次編號為Point1～Point5，如圖3所示。數據采集與分析的主要振動方向為圖3中所示y方向，高速攝像機拍攝視角為z正方向。

圖3 傳感器布放圖

2.3 實驗結果對比

2.3.1 固定頻率激勵

選取100 Hz作為激勵頻率。振動過程中使用高速攝像機以1920像素×1280像素、幀頻1000 f/s的參數進行拍攝。由傳感器獲取的5個測點的振動加速度信號，經過二次積分獲得振動位移信號，并以此作為參考。再以視覺測量技術的稠密光流法處理所攝視頻，手動選取相同5點并獲得振動數據。對2類數據同步化處理后結果如圖4所示。其中，紅色曲線為加速度傳感器所獲信號；藍色曲線為振動可視化方法所獲振動信號。

圖4 100 Hz激勵下的振動信號

由圖4可知，振動可視化方法所獲信號的頻率和相位與加速度傳感器所獲參考信號的重合度較高，但其振幅普遍小于參考值。這是由于視頻采集的幀頻過高，采集的圖像偶有失真現象產生，最終導致稠密光流法在計算物體運動量時產生了誤差。對2種方法獲得的振動峰峰值進行了誤差分析，結果如表1所示。

表1 振動峰峰值誤差對比

其中，2種方法在Point3與Point4處的振動數據誤差較大，誤差絕對值均大于10%，主要歸咎于振動可視化方法對測量點的手動選取產生的位置誤差。因此本誤差對ODS結果不產生影響。

此外，振動可視化方法還存在采樣頻率的限制，其振動分析最高頻率與高速相機的采集幀頻數值一致，但是最佳的振動分析頻率為采集幀頻的1/2。因此，如果需要獲得高的分析頻率，就需要更換更高幀率的高速相機。相比于傳統的振動數據采集方法，儀器成本高是該方法目前明顯的不足之處。本次測量參數為1920像素×1280像素@1000 f/s，即分析頻率為1000 Hz，最優分析頻率為500 Hz。

由上述2種方法得到了懸臂梁同一時刻的ODS結果。固定頻率100 Hz激勵下的ODS如圖5所示。圖5由上至下依次展示了：振動視頻中的懸臂梁、振動可視化方法所測得的懸臂梁ODS和加速度傳感器得到的參考ODS。從整體來看，振動可視化方法獲得的ODS結果中，背景噪聲較大。但分析懸臂梁的ODS可知，2種方法獲得的ODS表征較為一致。在Point3與Point4之間有正負位移交界處，2種方法的顯示結果一致。因此本文提出的方法能夠較為直觀地展示結構的振動情況。

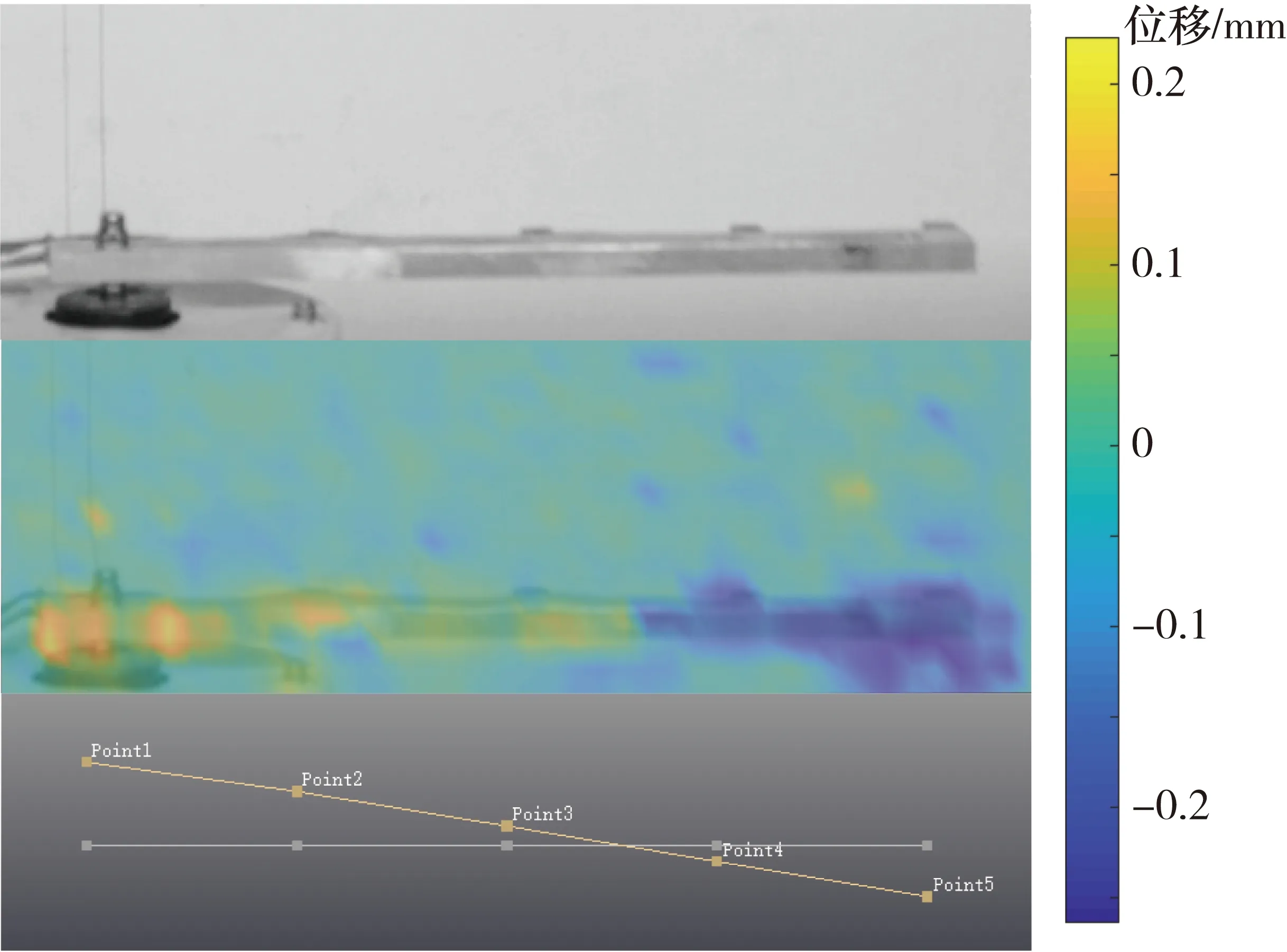
圖5 固定頻率100 Hz激勵下的ODS

2.3.2 固有頻率激勵

選取梁的一階固有頻率，即520 Hz，作為激勵頻率，觀察懸臂梁在共振情況下的ODS。考慮到上述部分結果中提到的背景噪聲問題，本次實驗通過在分析時僅選取目標梁的區域，以達到去除背景噪聲的目的。2種方法測量到的ODS結果如圖6所示。由圖6可以看出，2種方法在定性分析時的ODS結果基本一致。

圖6 固有頻率520 Hz激勵下的ODS

3 振動可視化應用

3.1 應用背景

懸臂梁的振動實驗驗證了振動可視化測量方法的可行性，因此將該方法應用于電力變壓器的振動測量中。變壓器振動可視化測量實驗如圖7所示，振動可視化測量所用裝置與懸臂梁實驗相同。

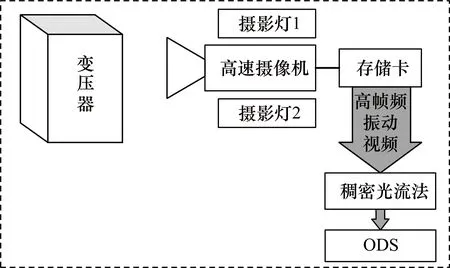
圖7 變壓器振動可視化測量實驗

圖8為實驗室變壓器，在實驗室中的10 kV變壓器上使用振動可視化方法進行ODS測量實驗。為測量不同振動狀態下的變壓器ODS，主要針對其上鐵軛進行螺栓松動。通過松動螺栓，達到了模擬變壓器異常狀態的實驗效果，螺栓松動程度對應變壓器的異常程度。本次實驗分別測量了以下狀態的變壓器ODS：螺栓100%最大扭矩(正常狀態)、左側螺栓60%最大扭矩、右側螺栓80%最大扭矩、右側螺栓20%最大扭矩。

圖8 實驗室變壓器

考慮到懸臂梁實驗中的背景噪聲問題，本次應用實驗中僅對視頻中電力變壓器的范圍進行分析。

3.2 應用結果

3.2.1 正常狀態

振動可視化方法測量電力變壓器正常運行時的ODS結果如圖9所示。可以看出，相比于設備全局振動情況，其繞組上的振動幅度較大。特別是兩側繞組的振動通過結構傳遞至箱體，振動幅度較大，符合電力變壓器振動傳遞原理。

圖9 正常狀態下的電力變壓器ODS

3.2.2 左側螺栓60%最大扭矩

將左側螺栓的扭矩調節為最大扭矩的60%，并采用振動可視化方法測量電力變壓器的ODS，結果如圖10所示。由圖10可知，螺栓的松動導致了變壓器振動狀態的改變，其整體的振動幅度較正常狀態時增大。左上角的箱體振動尤為明顯，這是由于左側螺栓松動后，箱體左側所受約束減小，振動幅度增大。

圖10 左側螺栓60%最大扭矩下的電力變壓器ODS

3.2.3 右側螺栓80%最大扭矩

將右側螺栓的扭矩調節為最大扭矩的80%，并采用振動可視化方法測量電力變壓器的ODS，結果如圖11所示。本次螺栓扭矩的調整幅度較小，由圖11可以看出，此次調整帶給整體振動狀態的改變較小。僅有中間的繞組處和箱體右上角處振幅與其他部位相比較大。這是由于右側螺栓松動后，箱體右側所受約束減小，其右上角遠離底部，剛度較小，因此振動幅度增大。

圖11 右側螺栓80%最大扭矩下的電力變壓器ODS

3.2.4 右側螺栓20%最大扭矩

將右側螺栓的扭矩調節為最大扭矩的20%，并采用振動可視化方法測量電力變壓器的ODS，結果如圖12所示。此次螺栓的松緊程度較低，振幅較大區域集中在變壓器整體的右上部分。其振動幅度由下至上逐漸增大，且右邊繞組上部的振動最大，進而傳遞至中間繞組上部。

圖12 右側螺栓20%最大扭矩下的電力變壓器ODS

從設備全局振動情況來看，電力變壓器的振動異常狀態在其ODS上的表現十分明顯。因此可將其作為運行狀態分析的參考，為狀態識別研究提供可視化結果支撐。

4 結束語

將視覺測量技術運用于電力變壓器的ODS測量中，提出用稠密光流法進行圖像處理中的運動信息捕捉，通過懸臂梁對比實驗驗證了該方法的可行性，將方法推廣應用于電力變壓器，實現了基于振動可視化技術對電力變壓器的ODS測量。結果表明：該方法能夠突顯設備結構振動狀態的差異。該方法有非接觸和易實現等優點，可推廣于狀態識別研究和電力設備故障診斷等領域。