基于光學掃描的高精度基準孔測量方法研究
陳 強, 陳代鑫, 雷 沛,2, 孫海龍,2, 代玉淋,2
(1.成都飛機工業(集團)有限責任公司,四川 成都 610092;2.四川省航空智能制造裝備工程技術研究中心,四川 成都 610092)
隨著飛機設計和制造的不斷發展,以及飛機裝配對效率、質量和精度要求的不斷提升,自動鉆鉚系統在國內外航空制造企業中得到了廣泛的研究和應用[1-6]。美國GE公司和EI公司、德國寶捷公司等都已經研發出了比較成熟的系統。在國內,一些高校、科研院所和企業對自動鉆鉚技術也做了深入研究,研制了自動鉆鉚系統。隨著自動鉆鉚系統的廣泛應用,提高自動鉆鉚的精度和質量成為了當前研究的熱點方向。飛機裝配中鉚釘孔的位置精度直接影響飛機的裝配質量和使用壽命,因此提升鉚釘孔位置精度具有十分重要的意義。
由于飛機零件加工誤差和裝配誤差的存在,導致飛機部件實際制孔位置與理論制孔位置存在一定的偏差。如果直接按照理論制孔位置對飛機部件進行制孔可能造成制孔位置超差,從而導致產品報廢。為了避免這種情況發生,在實際應用中通過在產品表面設置基準孔,利用基準孔位置對理論制孔位置進行糾偏,從而保證實際制孔位置精度滿足產品裝配±0.5 mm的精度要求。因此,保證基準孔位置的識別精度,對提高產品制孔位置精度具有決定性作用。國內外學者對基準識別進行了大量的研究,其中最主要的方法有單目視覺測量法和雙目視覺測量法。單目視覺測量只能計算出基準孔平面二維坐標[7-10],在飛機翼面類部件裝配中應用廣泛。但在大曲率飛機部件裝配的應用中,單目視覺測量需通過第三軸理論數據進行組合才能得到基準孔的三維坐標,由于此方法采用了部分理論數據導致測量精度不高,存在許多的弊端。雙目視覺測量通過兩個相機同時對基準孔進行測量,標定計算后得到基準孔的三維坐標,此方法的測量精度較高[11-12],但是雙目視覺測量需要2個工業相機導致測量裝置體積較大,在自動鉆鉚系統中安裝比較困難。
為此,本文提出了一種基于線激光掃描的基準找正方法,利用一個線激光掃描儀和一個伺服電機組成基準掃描裝置,對基準孔進行掃描測量,得到產品表面點云數據,最后通過邊界識別和橢圓擬合計算得到基準孔圓心三維坐標。該方法主要優勢在于激光線掃描裝置結構緊湊、安裝便利,可以與自動鉆鉚系統有效地結合;利用標準平面可實現激光線掃描裝置的快速標定,大幅提高了標定效率;激光線掃描裝置可直接實現基準孔圓心三維坐標測量,對實現大曲率飛機部件基準孔的精確測量以及提升制孔位置精度具有重要意義。
1 光學掃描儀標定
數字化鉆鉚系統采用五軸數控機床作為運動單元,其示意圖如圖1所示,包含X軸、Y軸、Z軸、A擺、B擺。線激光掃描基準找正原理如圖2所示。線激光掃描儀與伺服電機相連,伺服電機帶動線激光掃描儀對基準孔進行掃描。
建立與機床制孔末端執行器固連的坐標系O′-xyz,其中坐標原點與機床RTCP重合,當機床旋轉軸A、B旋轉角度均為0時,該坐標系3個軸的方向與機床坐標系O-xyz的3個軸的方向平行。
建立與機床制孔末端執行器固連的坐標系O″-xyz,當滑臺在原點時,坐標原點與線激光掃描儀測量原點重合,X軸和Z軸分別與線激光掃描儀光線測量坐標系X軸、Y軸平行。
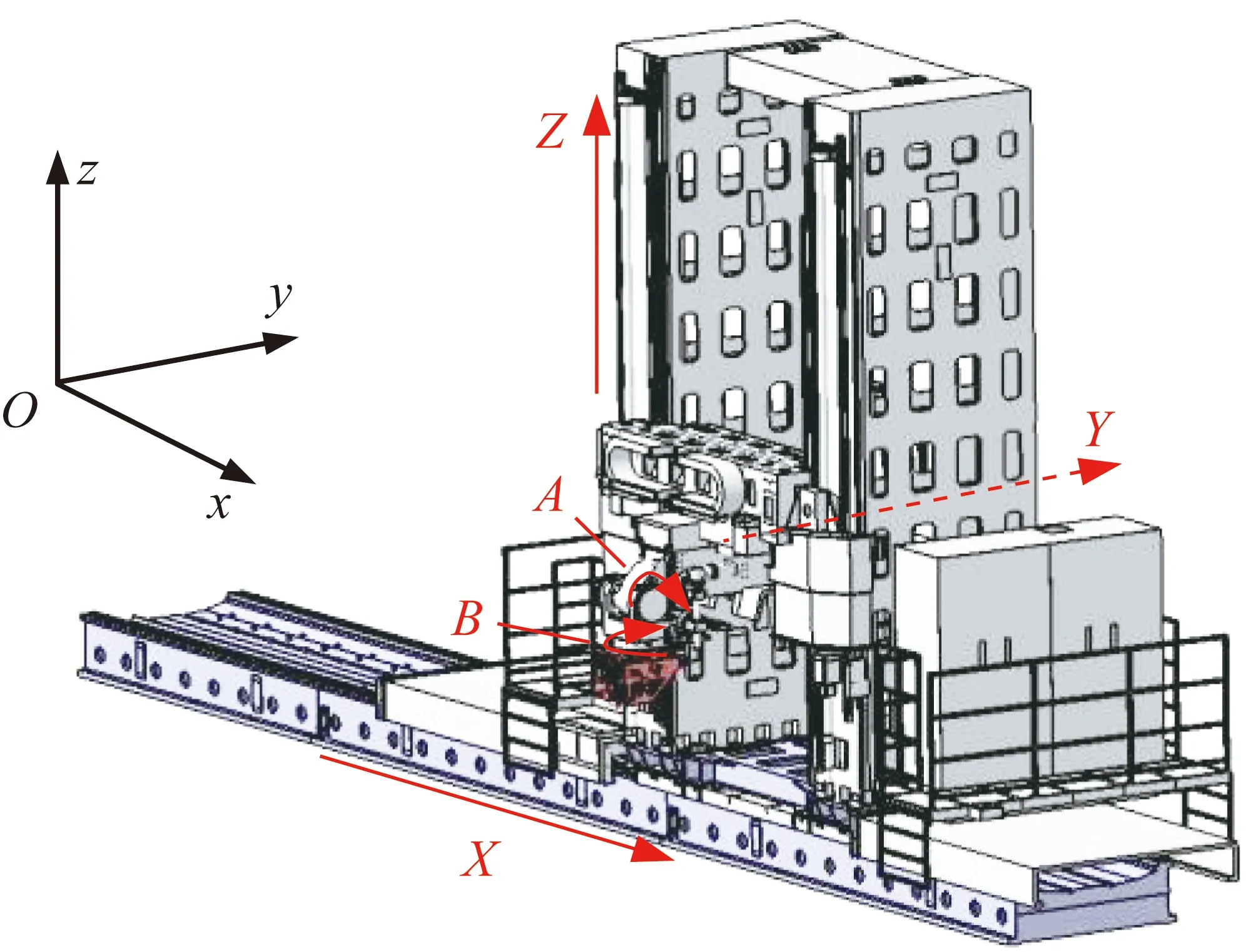
圖1 五軸加工機床示意圖
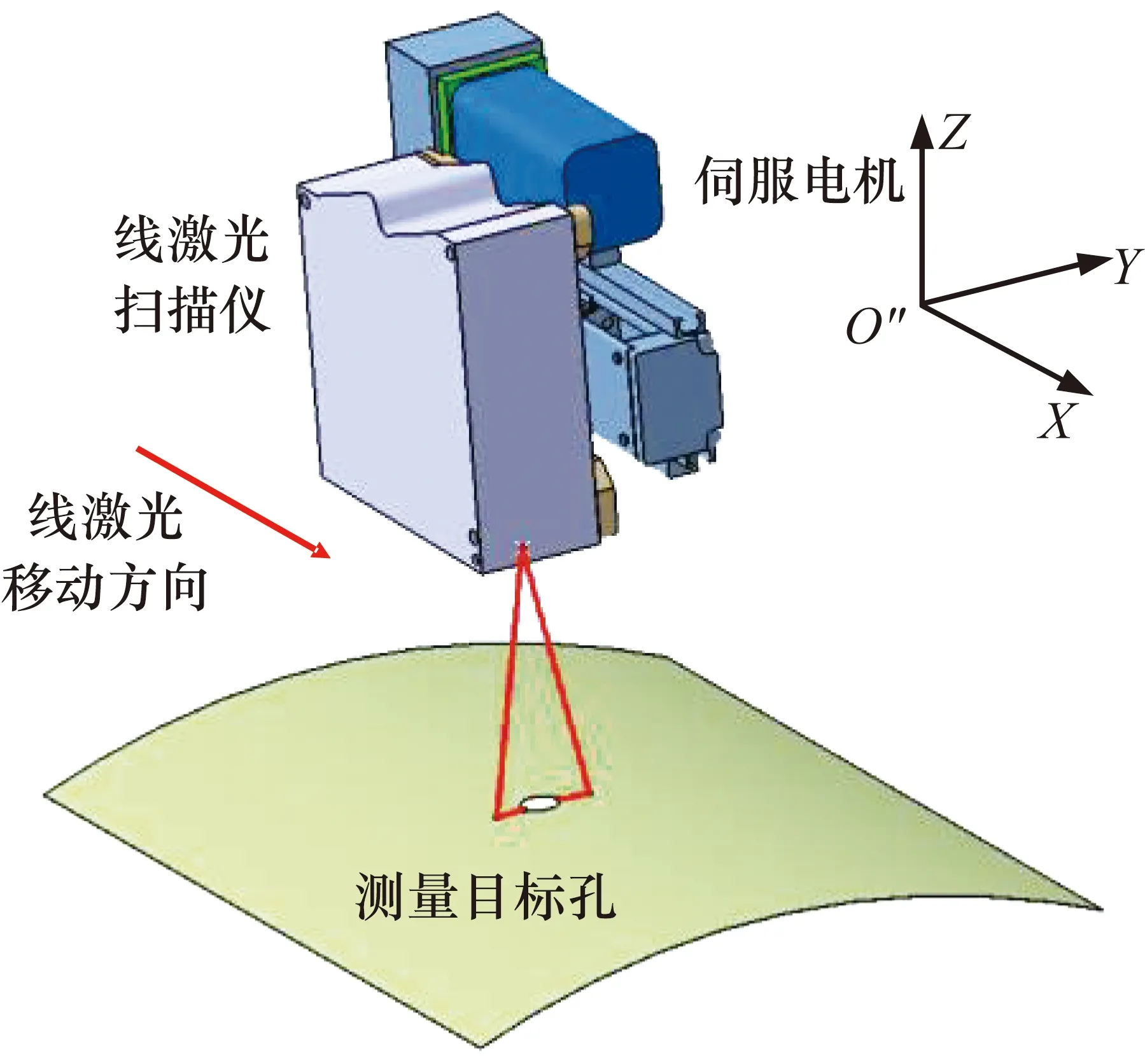
圖2 線激光掃描基準找正原理
(1)
假定基準平面在坐標系O′-xyz下的方程為
ax+by+cz=d
(2)
假定坐標系O″-xyz與坐標系O′-xyz之間的旋轉關系為
(3)
其中,R中元素滿足以下關系。
(4)
因此,可以得到測量點在坐標系O′-xyz下的坐標為
p′=p0+R·p″
(5)
式中:
(6)
將式(3)、式(5)和式(6)代入式(2),得到式(7)。令式(7)中Δy=0,可以得到式(8)。由9個相互不平行的基準面可以得到式(9)。
a·(x0+A1·(x+μ·Δy)+A2·v·Δy+A3·(z+ω·Δy))+b·
(y0+B1·(x+μ·Δy)+B2·v·Δy+B3+(z+ω·Δy))+
c·(z0+C1·(x+μ·Δy)+C2·v·Δy+C3·(z+ω·Δy))=d
(7)
a·(x0+A1·x+A3·z)+b·(y0+B1·x+B3·z)+
c·(z0+C1·x+C3·z)=d
(8)
ai·(x0+A1·x+A3·z)+bi·(y0+B1·x+B3·z)+
ci·(z0+C1·x+C3·z)=di,i=1,…,9
(9)
將式(9)改寫為矩陣形式:
A1X1=D1
(10)
其中A1、X1、D1分別如式(11)、(12)、(13)所示。
(11)
(12)
(13)
利用矩陣運算可得:
(14)
利用式(4)可以求解得A2、B2和C2。
令式(7)中x=0,可得:
a·(x0+A1·μ·Δy+A2·v·Δy+A3·(z+ω·Δy))+
b·(y0+B1·μ·Δy+B2·v·Δy+B3·(z+ω·Δy))+
c·(z0+C1·μ·Δy+C2·v·Δy+C3·(z+ω·Δy))=d
(15)
由3個相互不平行的基準面可得:
(ai·A1+bi·B1+ci·C1)·Δyi·μ+(ai·A2+bi·B2+ci·C2)·Δyi·
v+(ai·A2+bi·B2+ci·C2)·Δyi·ω=di,i=1,…,3
(16)
將式(16)改寫成矩陣形式為
A2X2=D2
(17)
式中:A2、X2、D2分別如式(18)~式(20)所示。
(18)
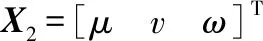
(19)
(20)
利用矩陣運算,可以求得:
(21)
坐標系O′-xyz與機床坐標系O-xyz之間的關系為
R(α,β)=Rx(α)Rz(β)
(22)
式中:α為機床A擺角度;β為機床B擺角度。
(23)
(24)
機床RTCP點在機床坐標系O-xyz下的坐標為
(25)
因此,可以得到測量點在機床坐標系O-xyz下的坐標為
PS=P+R(α,β)·p′
(26)
2 基準孔識別
利用線激光掃描儀對基準孔進行掃描,通過式(1)可以計算得到基準孔及附近曲面在坐標系O″-xyz下的點云坐標集為
P″={p″(i)},i=1,…,n
(27)
當滑臺移動距離Δy為定值時,線激光掃描儀測量得到的點云集如圖3所示。定義點云集相鄰兩點之間z軸坐標值變化量為Δz,X軸坐標值變化量為Δx,其中Δx為定值。由于飛機表面的光順性,設定飛機表面任意相距Δx兩點之間Δz的最大值為ε。
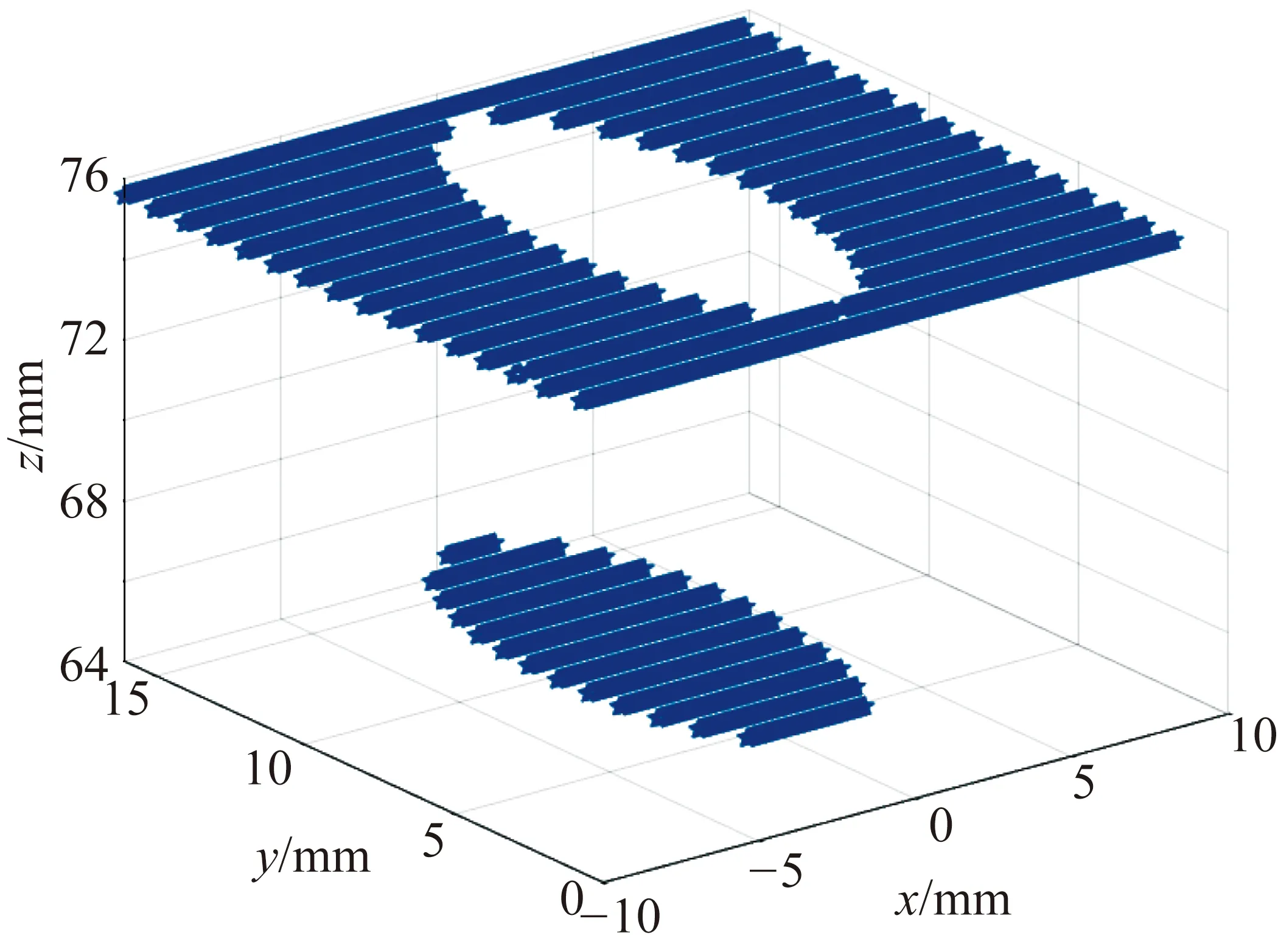
圖3 基準孔點云集
建立目標函數為
(28)
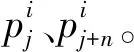
(29)
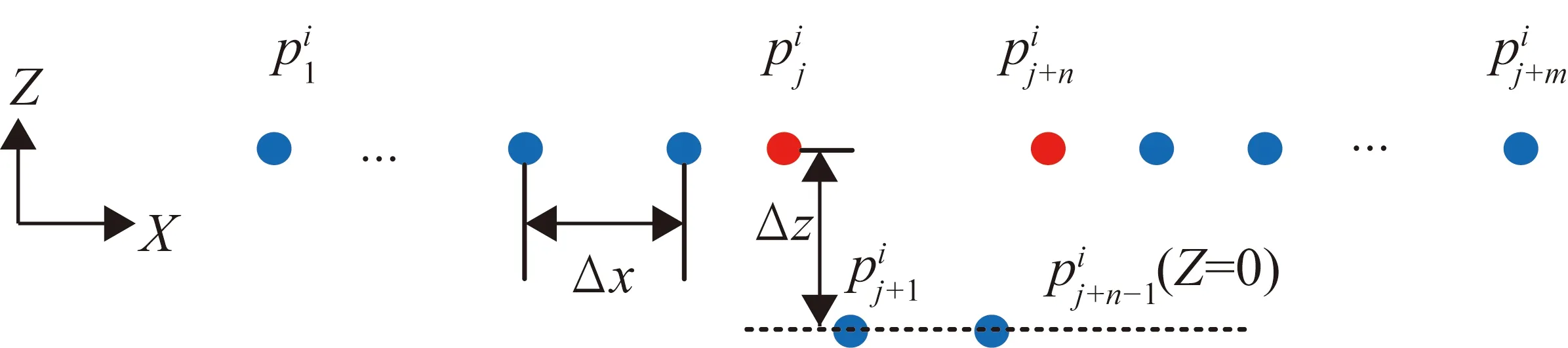
圖4 邊界提取原理
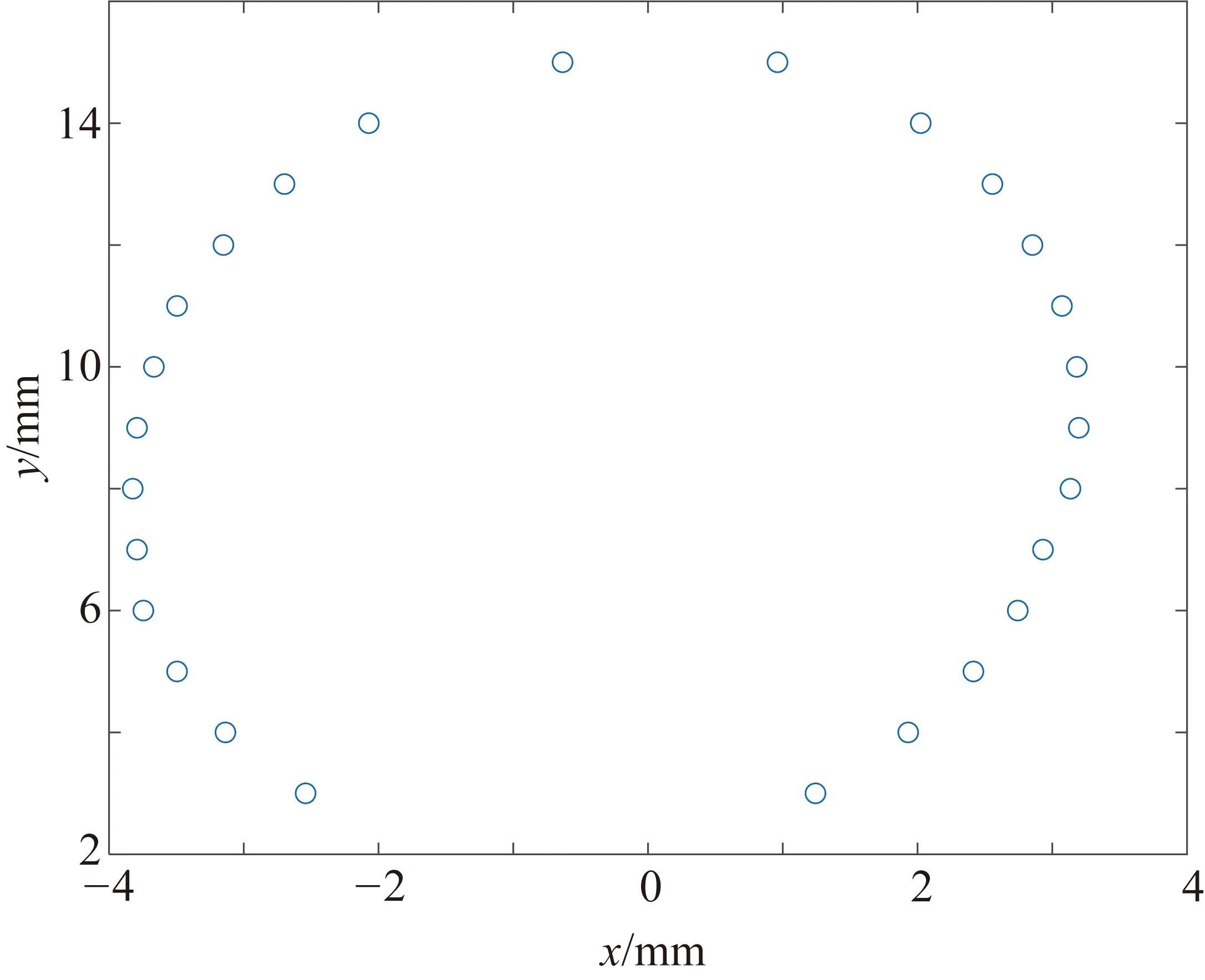
圖5 邊界點平面圖
平面橢圓一般方程為
x2+Axy+By2+Cx+Dy+E=0
(30)
利用式(30)可以求解出基準孔圓心的x、y坐標為
(31)
(32)
利用最小二乘法對橢圓進行擬合,使式(32)取值最小,則有:
(33)
由式(33)可以得到正定方程組為
TC=K
(34)
其中:
(35)
(36)
(37)
利用矩陣運算可以求得橢圓方程系數為
C=(TTT)-1TTK
(38)
利用式(31)可以計算出橢圓圓心坐標。
(39)
3 實驗驗證
實驗采用圖6所示的五軸加工機床,其技術參數如表1所示。鉆鉚末端執行器包含制孔和抽鉚功能,如圖7所示。線激光掃描儀采用的是某公司生產的二維掃描傳感器,其參數如表2所示。
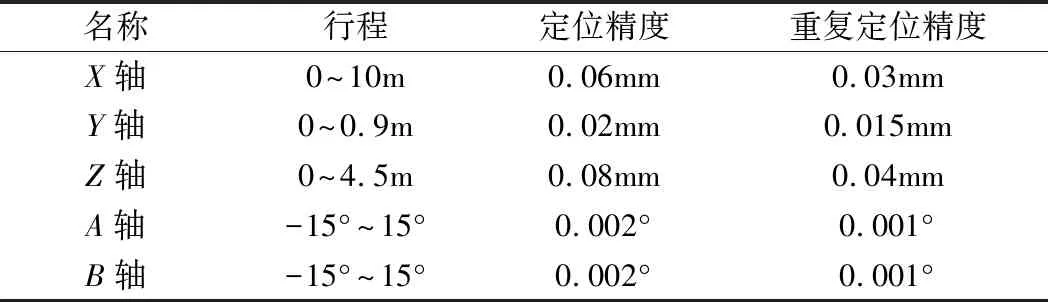
表1 機床技術參數

圖6 五軸加工機床

圖7 鉆鉚末端執行器
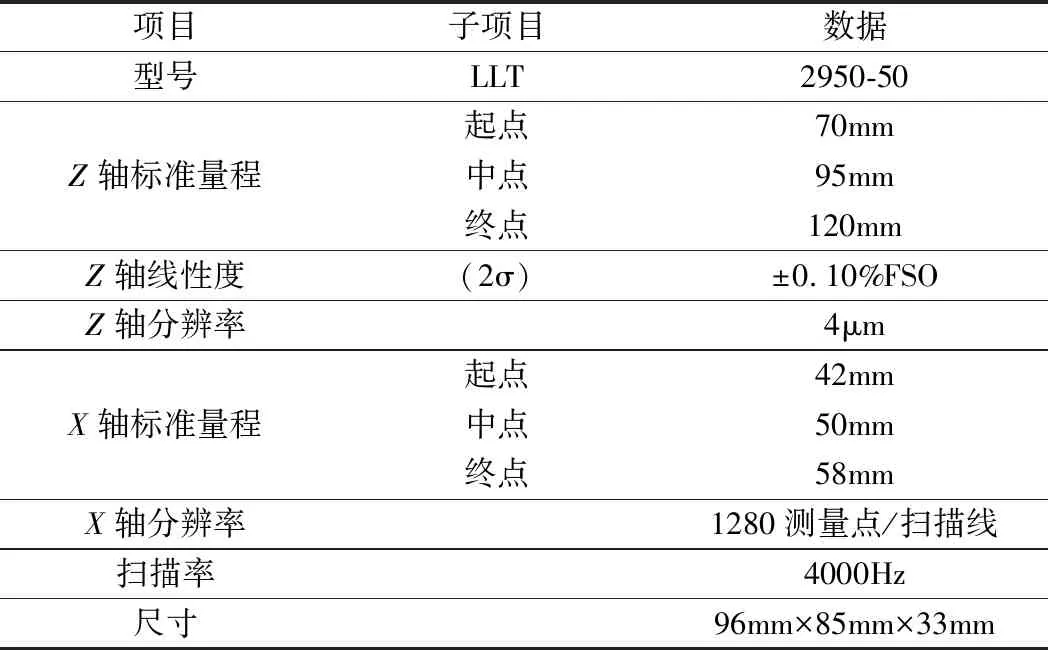
表2 線激光掃描儀參數
利用機床末端執行器上的掃描儀對測量孔進行測量并針對不同掃描步長進行了測試,最終與激光跟蹤儀(型號Leica AT960,測量精度±0.01 mm)測量的數據進行對比,實驗結果如表3所示。
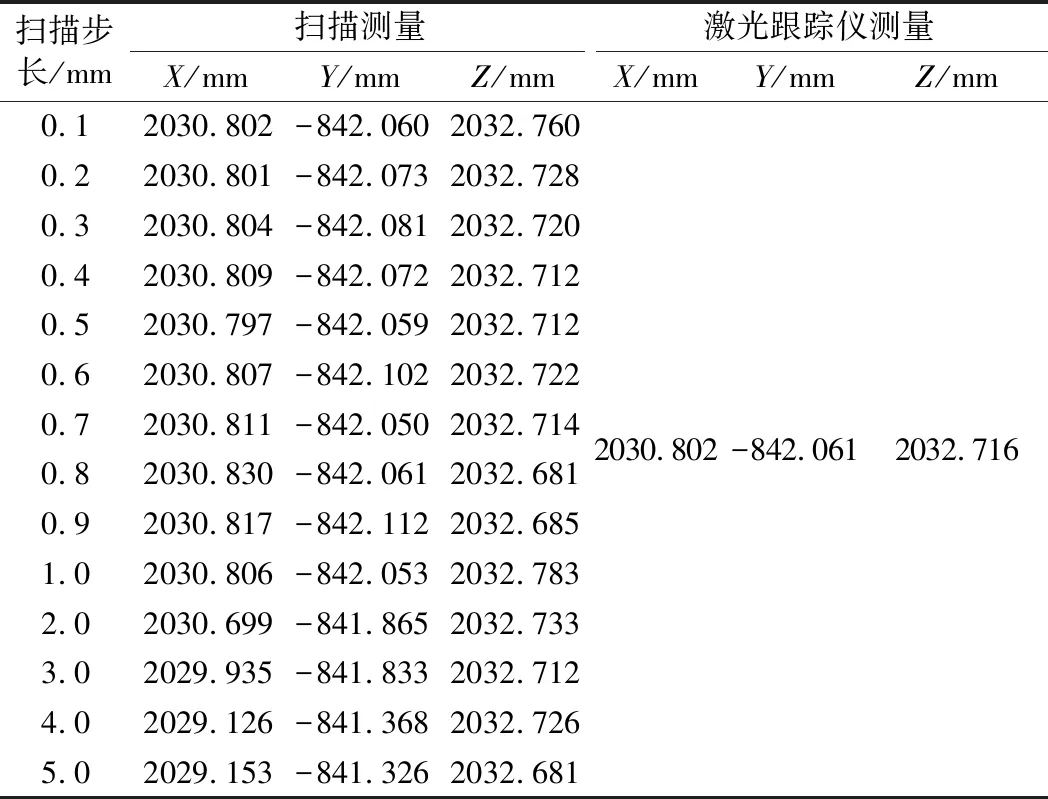
表3 實驗結果
其中測量孔直徑為10 mm,精度為H9。掃描儀距離測量孔距離范圍為90~110 mm。掃描儀X軸長度分辨率計算公式為
(40)
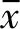
根據式(40),可以得到在驗證條件下,X軸分辨率為0.0378125~0.0428125 mm。
從表3中數據可以看出,當掃描步長在0.1~1 mm之間變化時,掃描測試結果始終保持一致,且與激光跟蹤儀的測量結果誤差始終保持在±0.1 mm之內。當掃描步長增大至2 mm時,測量結果與激光跟蹤儀結果誤差在0.2 mm。但掃描步長增大至3 mm以上時,誤差達到了1 mm。造成此現象的主要原因為當掃描步長增大至3 mm以上時,直徑為10 mm的測量孔掃描得到的包含孔邊界的數據量變小,從而導致擬合精度降低。
從表1可看,機床的定位精度優于±0.1 mm。因此,針對直徑為10 mm的基準孔,掃描步長在2 mm以下時,通過該方法進行基準識別,可以使制孔位置精度滿足飛機裝配±0.5 mm的精度要求。
4 結束語
本文提出了一種適用于數字化鉆鉚系統的高精度基準找正技術。首先,采用一個線激光掃描儀和伺服電機組成集成基準掃描裝置,機械地對基準孔和附近特征進行掃描,得到測量點數據集;然后,利用基準孔特性對測量點數據進行邊界提取,并采用最小二乘法進行橢圓擬合計算,得到基準孔圓心坐標;最后,利用標定出的基準找正裝置坐標系與機床坐標系的轉換關系計算得到基準孔在機床坐標系下的位置。實驗證明該方法能夠用于數字化鉆鉚系統的基準找正,滿足飛機裝配精度要求。同時,該方法可以針對不同應用場景和精度要求調節激光線掃描儀的掃描步長,從而控制基準孔識別精度。相對于單目視覺測量,該方法可以實現基準孔三維坐標的準確測量;相對于雙目視覺測量,該方法使用的測量裝置體積較小,便于安裝和布置;相對于利用激光跟蹤儀進行測量,該方法在整個測量和計算過程中不需要人工介入,系統自動化程度更高,整個測量速度更快。

