基于響應面法的分級注水泥器結構優化*

徐瑞強 孫興偉 劉寅 楊赫然 董祉序

(沈陽工業大學機械工程學院；遼寧省復雜曲面數控制造技術重點實驗室)

0 引 言

分級注水泥器作為分級固井過程中的關鍵部件，是實現一級固井與二級固井之間連續作業的重要保障[1-2]。通常情況下，分級注水泥器在流體沖擊力及熱力共同作用的耦合場下運行[3-4]，而且分級注水泥器本體與滑套之間具有一定的配合間隙。因此，為保證配合性質，其結構剛度要滿足一定的要求。然而分級注水泥器在實際使用過程中并不能完全達到固井需求，經常由于結構變形造成循環孔打開或關閉失敗。

利用響應面法，通過目標函數和約束函數的響應面模型預測非試驗點的響應值，利用試驗設計理論對指定的設計點集進行測試,可以有效提高優化效率[5-7]。其中，方波等[8]運用ANSYS Workbench軟件對外嚙合齒輪泵泵體在有限元分析的基礎上進行結構優化，優化后泵體變形及應力集中均明顯減小。包凱等[9]以鉆井現場普遍使用的楔形節流閥為例，對蓋體的結構進行優化，使得閥芯所受的應力與變形均達到最小，延長了節流閥的使用壽命。趙安[10]基于熱流固耦合理論對雙螺桿擠出機的機筒進行有限元分析及結構優化，通過拓撲優化使得筒體質量大幅減輕，結構等效應力明顯下降。陳新海等[11]對固井用浮箍結構進行優化，結果表明多相流中固相體積分數越大，對閥體的沖蝕越嚴重，浮箍開度越大，沖蝕速率越小。王志成等[12]采用多目標優化算法對自由曲面的網格結構進行優化，結果表明優化后結構應變能降低了21.2%。ZHANG L.F. 等[13]以柔性鉸鏈為研究對象，采用多目標優化方法對熱力耦合作用下鉸鏈結構設計參數進行優化，選取鉸鏈結構的4個關鍵參數作為設計變量，在ANSYS軟件中得出最優參數組合。LU Y.等[14]基于非支配排序遺傳算法和RBF響應面，在2 400 r/min工況下對飛機發動機氣門參數進行優化，結果表明發動機功率可提高1.63%。M.S.RAHUL 等[15]采用非支配排序GA-Ⅱ方法生成非支配解，采用多目標優化算法，對彈簧絲徑、螺旋彈簧直徑、彈簧圈數等設計參數進行了優化，得到了Pareto最優解。

本文考慮到分級注水泥器工作環境中的熱流固耦合作用，采用響應面優化方法對分級注水泥器本體和滑套的5個關鍵參數進行改進，以達到提高結構剛度的目的，從而避免固井過程中由于結構變形導致循環孔打不開或關不上的失效現象發生。

1 固井工況

以某油井的實際固井工況為例，該油井實際井深4 430 m，分級注水泥器安裝在井深2 200 m處，固井方式為分級固井。其中，一級固井封固分級注水泥器以下井段，二級固井封固分級注水泥器以上井段。固井注入的流體參數如表1及表2所示。

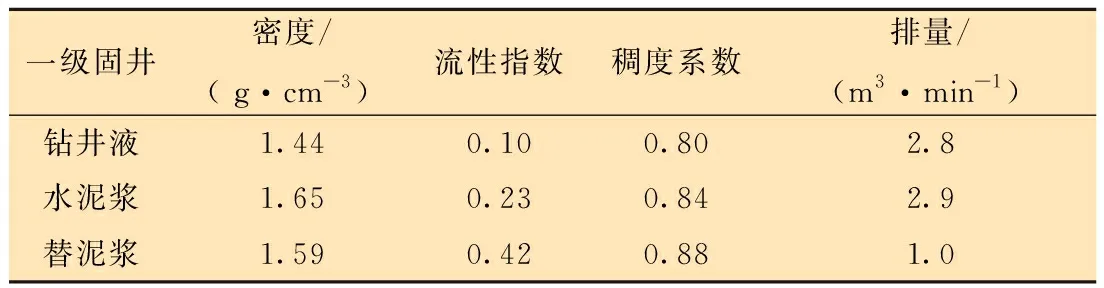
表1 一級固井注入流體參數Table 1 Injection fluid parameters for the 1st stage of cementing

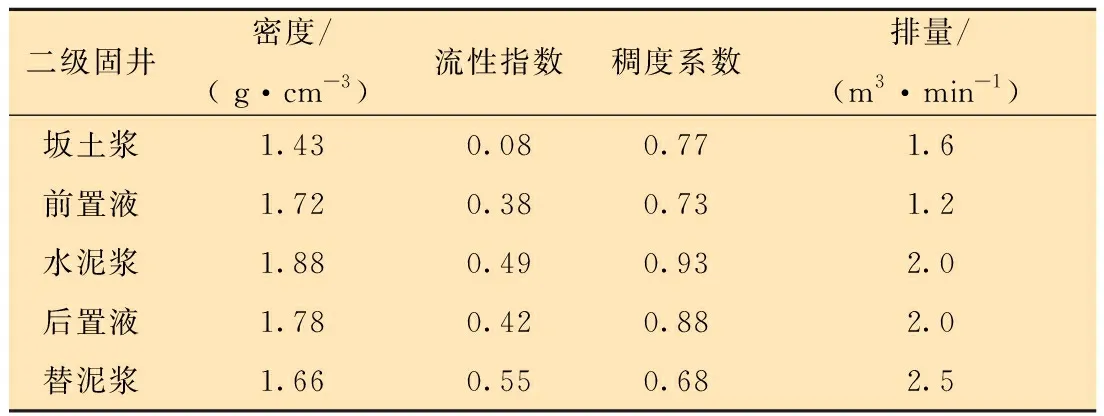
表2 二級固井注入流體參數Table 2 Injection fluid parameters for the 2nd stage of cementing

2 熱流固耦合分析

2.1 有限元模型建立

依據某油井實際使用分級注水泥器建立三維有限元模型(見圖1)，模型最大外徑282.5 mm，總長1 210 mm，最小內徑220 mm，額定載荷3 000 kN，密封強度50 MPa。本體與滑套之間配合間隙為1.5 mm，循環孔的打開與關閉依靠滑套移動剪斷剪切銷釘來實現。分級注水泥器的材料參數見表3。

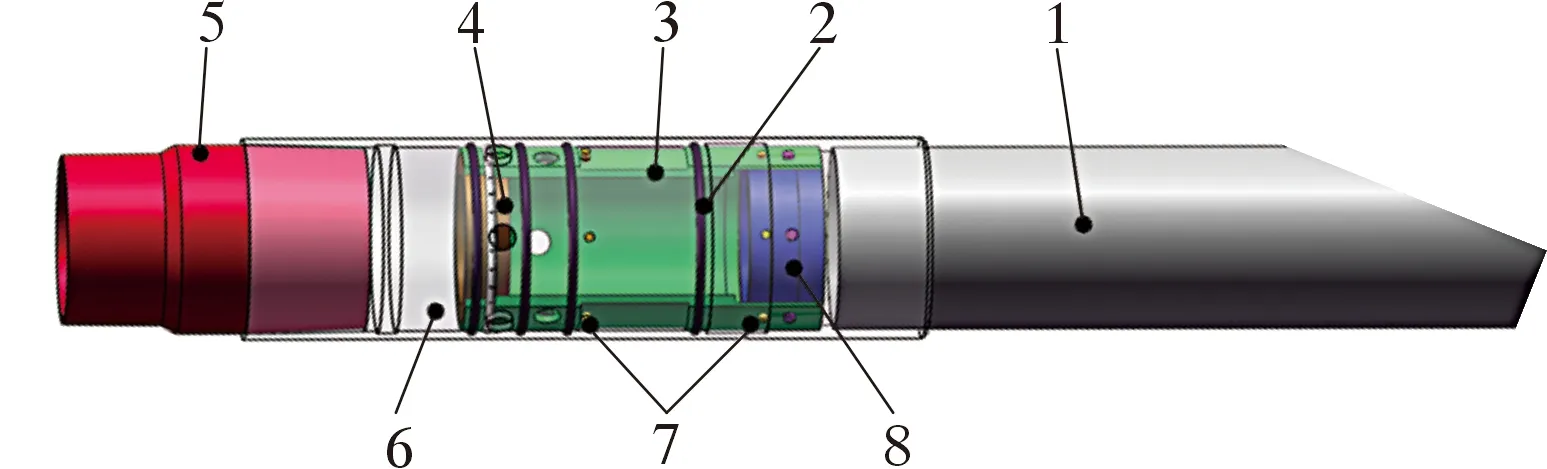
1—套管;2—密封圈;3—滑套;4—打開塞座;5—下接頭 ;6—本體;7—剪切銷釘;8—關閉塞座。圖1 分級注水泥器三維模型Fig.1 Three-dimensional model of the stage cementing collar

表3 分級注水泥器材料參數Table 3 Material parameters of the stage cementing collar

2.2 結構變形分析

固井過程中分級注水泥器受到井下高溫高壓流體作用。

圖2為一級固井時注水泥漿過程中滑套產生的變形云圖。由圖2可知，在管內流體和井下溫度的共同作用下，滑套產生徑向膨脹，最大變形量1.417 mm，位于循環孔處。此外，由于滑套內部安裝關閉塞座位置處的壁厚小于其他部位，所以也產生較大變形。

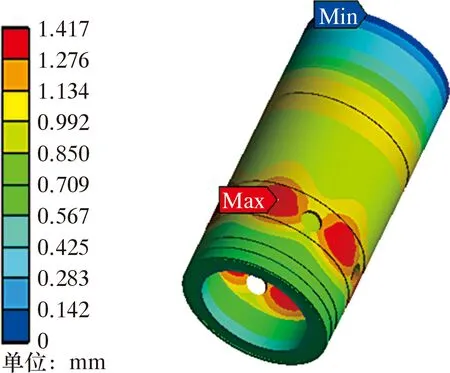
圖2 滑套變形云圖Fig.2 Deformation nephogram of the sliding sleeve

圖3為分級注水泥器本體在環空流體及溫度共同作用下產生的縮徑變形云圖。由圖3可知，最大變形主要集中在安裝剪切銷釘處，最大變形為0.62 mm，這是因為該位置的壁厚小于其他位置。

圖3 本體徑向變形云圖 Fig.3 Deformation nephogram of the stage cementing collar body radial

圖4為鉆井液浮力和環空流體壓力綜合作用下分級注水泥器本體產生的總變形，最大總變形量2.486 mm，變形同時包含徑向縮徑和軸向拉伸。

圖4 總變形云圖Fig.4 Deformation nephogram of the total

3 模型建立與多目標優化

3.1 參數化建模

首先在三維建模軟件中對模型的關鍵尺寸進行參數化，分別選擇滑套和本體各5個關鍵參數作為設計變量。圖5是滑套的5個設計變量示意圖。其中，D1為循環孔直徑，D2為關閉塞座安裝位置內徑，D3為滑套內徑，L4為中間滑套位置的軸向長度，L5為下端滑套位置的軸向長度。圖6是分級注水泥器本體5個設計變量的示意圖。其中，l1為本體循環孔中心至卡簧槽上邊緣的距離，d2為本體循環孔直徑，d3為剪切銷釘位置處的本體內徑，d4為本體最大外徑，l5為用于安裝滑套的軸向長度。

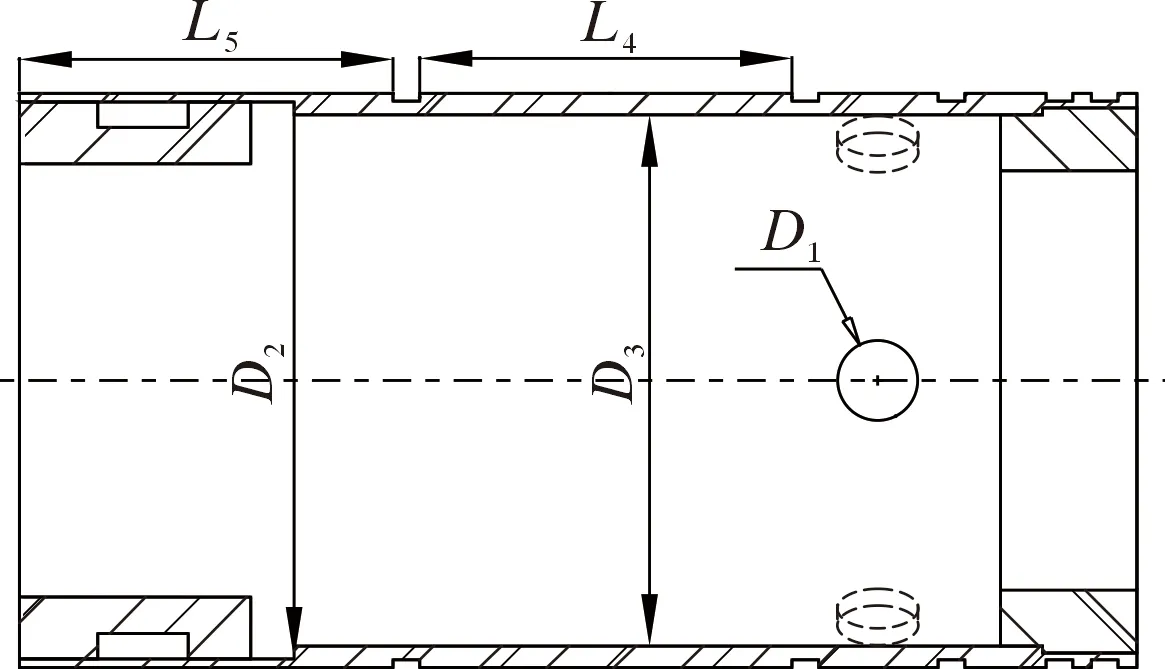
圖5 滑套優化參數Fig.5 Optimization parameters of the sliding sleeve

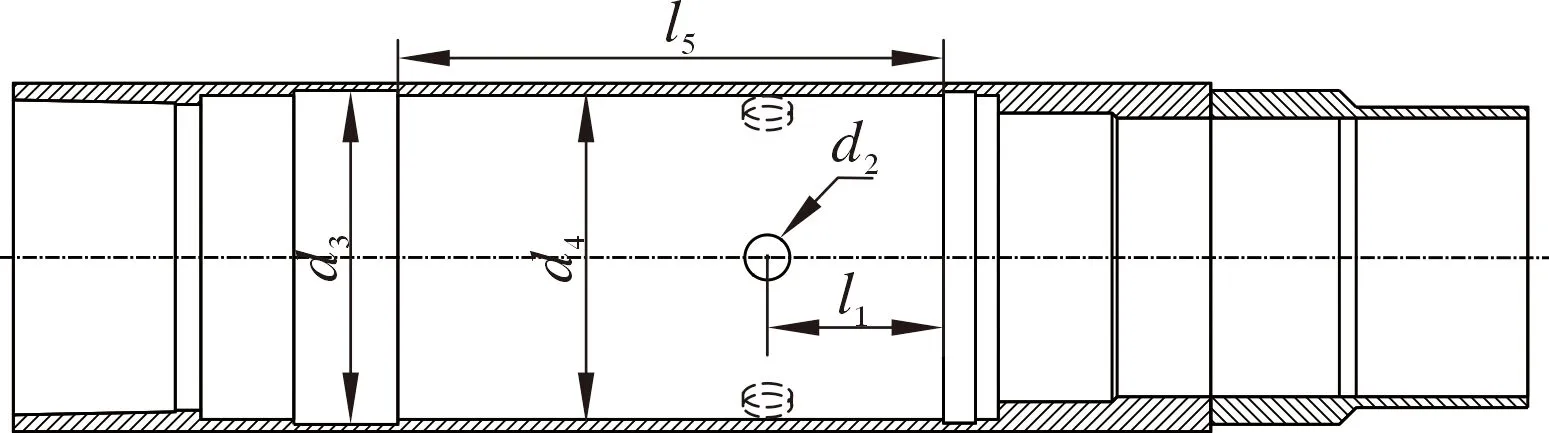
圖6 本體優化參數Fig.6 Optimization parameters of the stage cementing collar body

分級注水泥器滑套和本體的優化參數取值范圍如表4和表5所示。各個設計變量的取值范圍應符合實際參數設計的變化范圍。

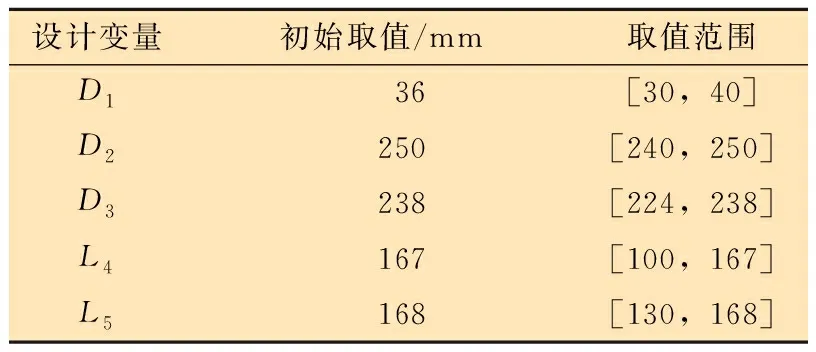
表4 滑套設計變量取值范圍Table 4 Value ranges of design variables of the sliding sleeve

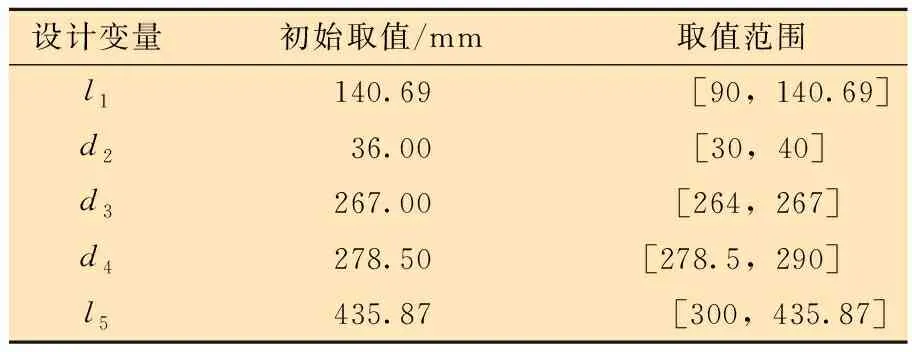
表5 本體設計變量取值范圍Table 5 Value ranges of design variables of the main cementing collar

3.2 試驗設計

常規的試驗設計方法有全因子設計、蒙特卡洛抽樣、均有抽樣及拉丁超立方抽樣等。其中拉丁超立方抽樣方法是將所有設計變量在變量空間中劃分為無數個水平，然后將每個變量的水平隨機組合，該方法有效解決了蒙特卡洛抽樣中樣本量大、采樣效率低的問題，并利用分層的思想提高了低樣本量條件下的采樣效率。因此本文采用拉丁超立方抽樣方法設計試驗。通過拉丁超立方抽樣試驗設計方法設計滑套與本體的27組試驗，見表6和表7。

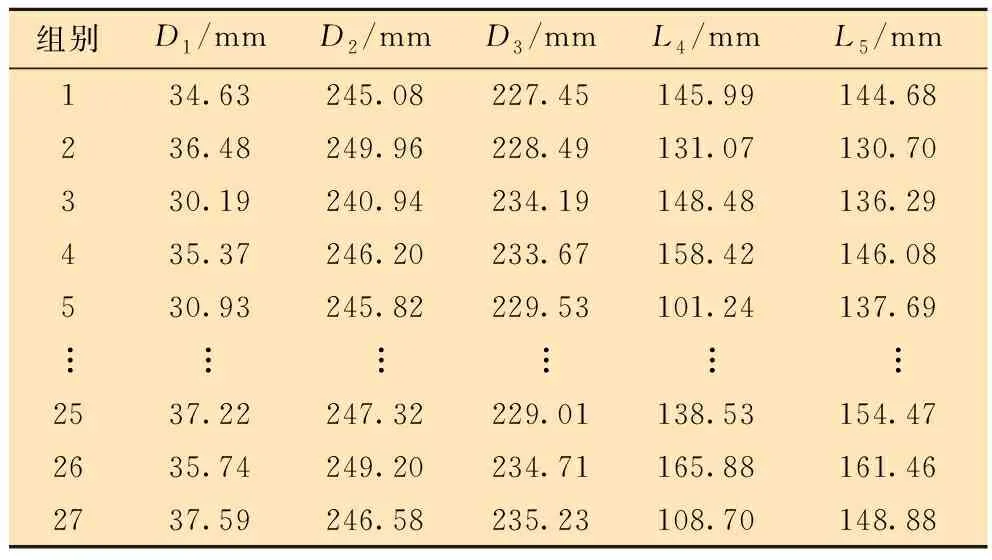
表6 滑套試驗設計Table 6 Sliding sleeve testing design

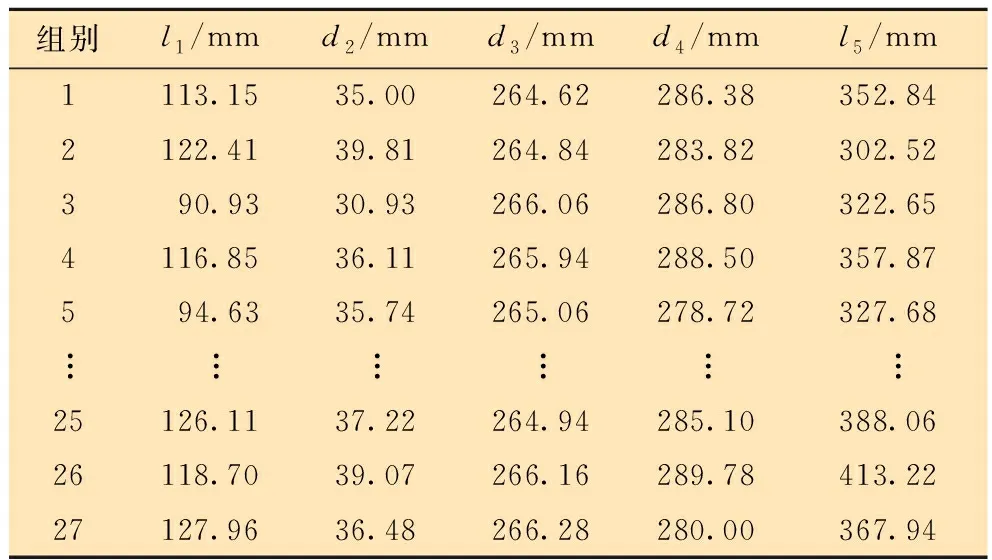
表7 本體試驗設計Table 7 Main cementing collar testing design

3.3 參數敏感性分析

參數敏感性可以反映設計變量對輸出結果的影響程度。結構參數優化時需同時優化多個參數，通過參數敏感性分析可以直觀地看到對目標函數影響最明顯的參數，同時在進行優化時可以忽略掉對目標函數影響較小的參數。利用ANSYS的靈敏度分析模塊對滑套和本體的5個設計變量進行敏感性分析。圖7為滑套參數敏感性圖。由圖7可以看出，對滑套質量影響最敏感的參數為D3、L4和L5，對滑套總變形影響最敏感的參數為D1和D3。

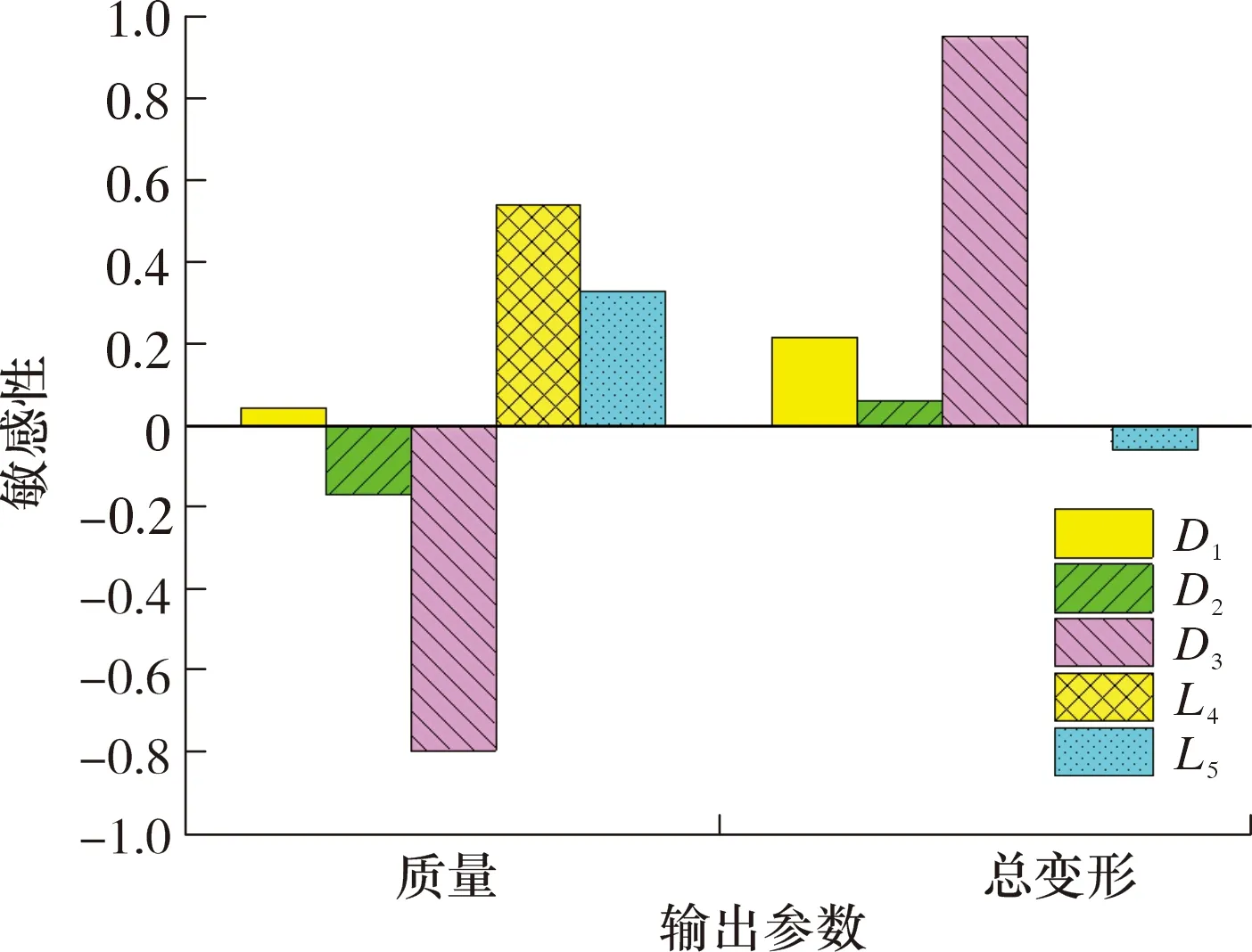
圖7 滑套參數敏感性圖Fig.7 Sensitivity analysis of the sliding sleeve

圖8為分級注水泥器本體參數敏感性圖。由圖8可以看出，對質量影響最敏感的參數為d4和l5，對總變形影響最敏感的參數為d4和l5，對徑向變形影響最敏感的參數為d2、d3和d4。

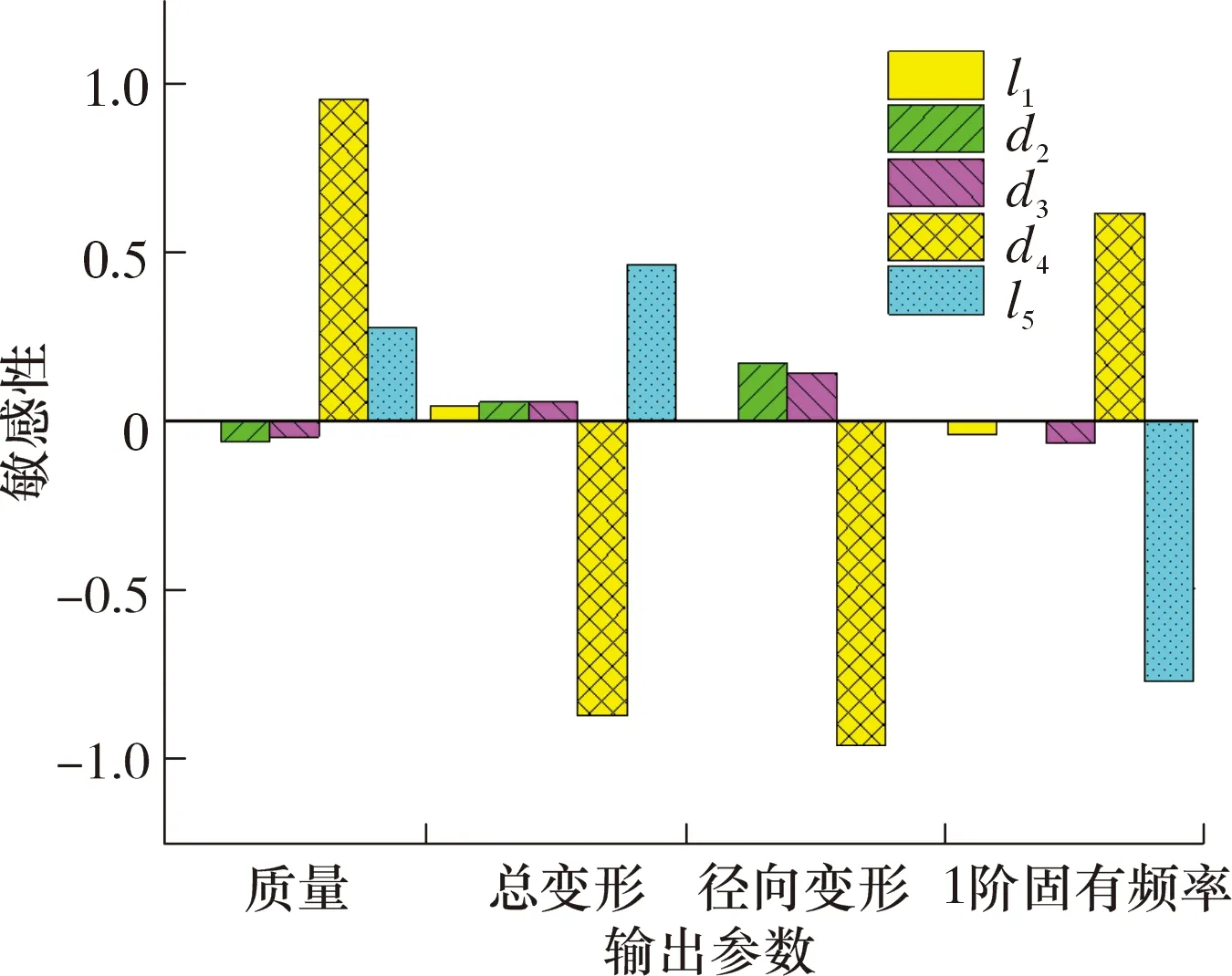
圖8 本體敏感性圖Fig.8 Sensitivity analysis of the stage cementing collar body

3.4 響應面擬合誤差

基于Kriging插值法構造響應面模型。響應面模型準確性是通過擬合優度指標R來驗證的，R的取值范圍為[0,1]，R越接近于1表示構造的響應面模型越準確，反之則差距越大。R的計算公式為：

(1)

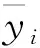
圖9和圖10分別為滑套和本體的優化目標計算值與預測值的擬合優度圖。由圖9和圖10可以看出，滑套質量、滑套總變形量、本體總變形、最大徑向變形和本體質量的樣本點都分布在對角線附近，這說明生成的響應面與試驗設計所得樣本點的一致性較好，擬合精度較高。

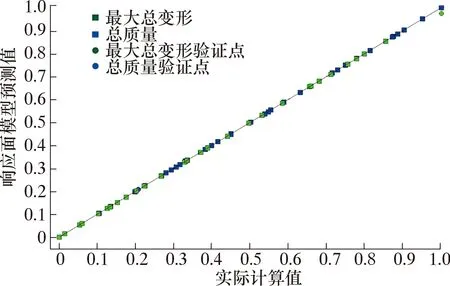
圖9 滑套試驗組誤差Fig.9 Prediction errors of the response surface methodology for the sliding sleeve

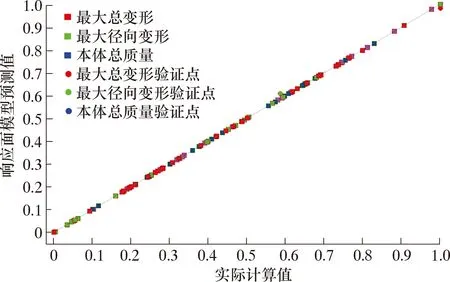
圖10 本體試驗組誤差Fig.10 Prediction errors of the response surface methodology for the stage cementing collar body

3.5 響應面建立

通過參數敏感性分析，選擇對滑套輸出參數影響最敏感的參數構建響應面。圖11為滑套的變形響應面，響應面上最大總變形為0.788～1.462 mm。

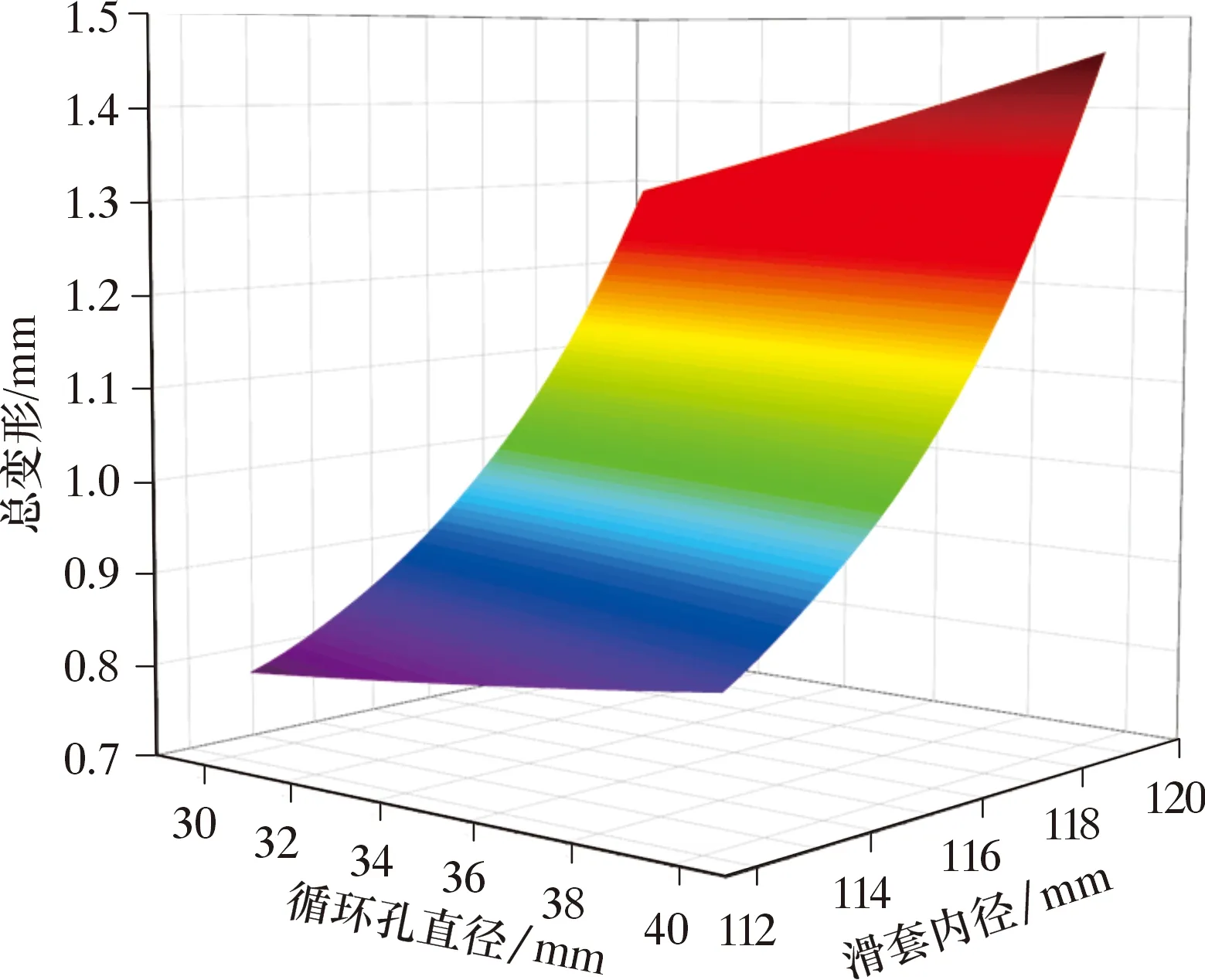
圖11 滑套變形響應面Fig.11 Response surface of the sliding sleeve deformation

圖12為本體徑向的變形響應面。由圖12可知，徑向的變形范圍為0.271～0.599 mm。圖13為本體總變形響應面。由圖13可見，總變形的變化范圍為1.790～2.482 mm。

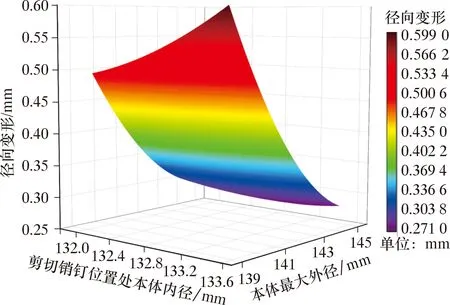
圖12 本體徑向變形響應面Fig.12 Response surface of the radial deformation of the stage cementing body

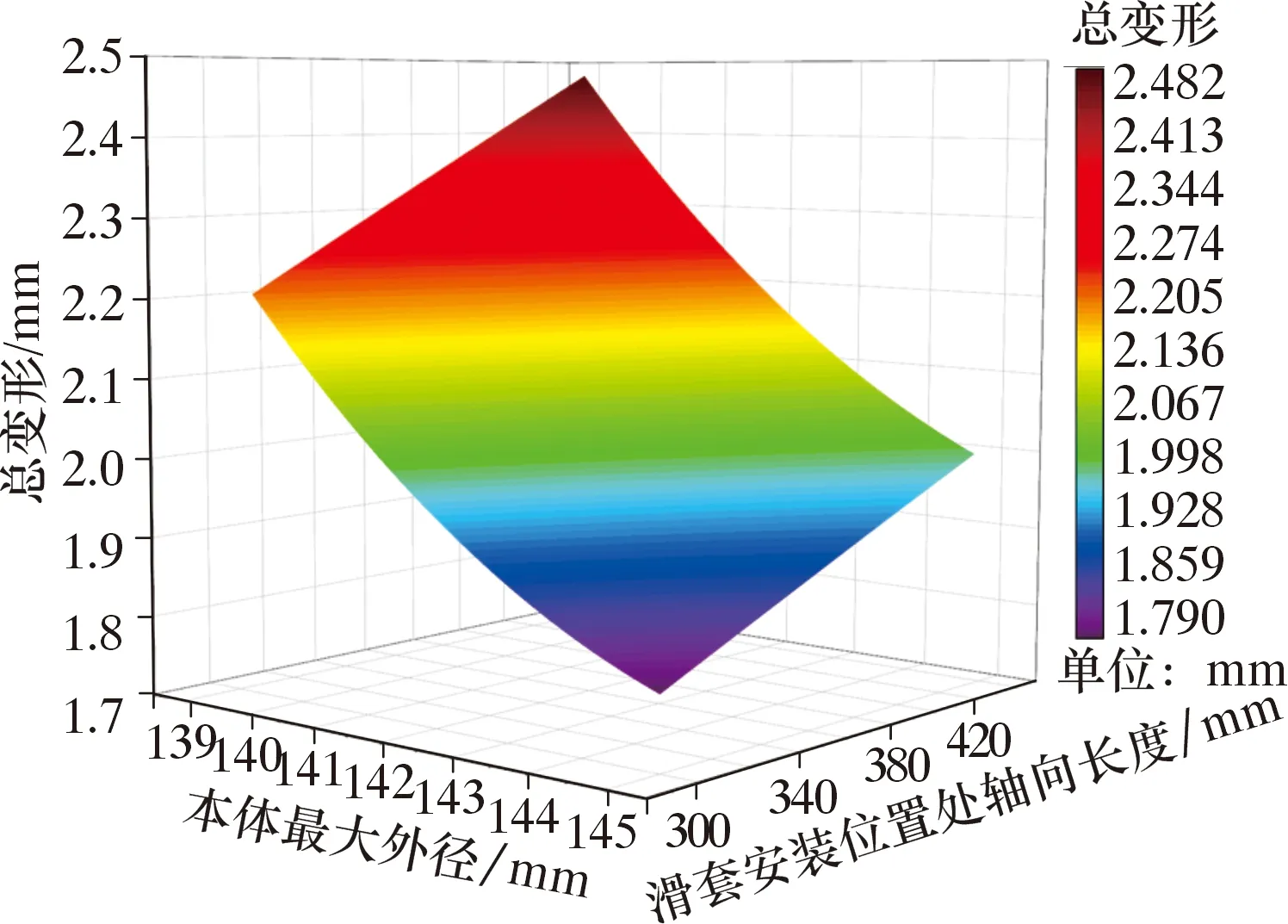
圖13 本體總變形響應面Fig.13 Response surface of the total deformation of the stage cementing body

3.6 滑套多目標優化數學模型

在對分級注水泥器滑套進行參數優化時，需滿足滑套在注水泥工況下變形量最小的條件，在此條件下可合理改變滑套質量。通過熱流固耦合分析可知，分級注水泥器結構變形是循環孔打開與關閉失效的主要原因，因此將滑套的5個設計參數作為設計變量，將滑套最大形變、滑套質量設置為輸出結果，即優化目標函數F(x)，輸入參數的變化范圍作為約束條件：

(2)

式中：d(x)為滑套產生的變形量；t(x)為滑套的質量；xi、ximin、ximax分別為設計參數、設計參數最小值及設計參數最大值，i=1，2，…，27。

3.7 本體多目標優化數學模型

二級固井時在注水泥工況下本體產生的變形量同樣最大，其中本體的徑向縮徑變形是分級注水泥器循環孔打開或關閉失敗的主要原因。為了使分級注水泥器在固井時可正常打開，將本體的5個設計輸入參數作為設計變量，本體徑向最大變形及本體質量設置為輸出結果，即優化目標函數F(y)，輸入參數的變化范圍作為約束條件：

(3)

式中：d(y)為本體產生的變形量；t(y)為本體質量；f(y)為本體的1階固有頻率；yi、yimin及yimax分別為設計參數、設計參數最小值及設計參數最大值，i=1，2，……，27。

4 優化結果分析

通過多目標優化方法，在有限元分析軟件中得到經優化后使分級注水泥器滑套和本體的徑向變形及總變形最小的最優參數組合。將優化后的參數進行圓整得到最優參數組合，如表8和表9所示。

表8 滑套設計變量最優解Table 8 Optimal solutions of the sliding sleeve design variables

表9 本體設計變量最優解Table 9 Optimal solutions of the main cementing collar design variables

圖14為優化后滑套在一級固井時注水泥工況下的變形分布云圖。由圖14可以看出，優化后滑套最大變形量為0.747 mm，通過響應面優化并圓整后的參數略低于滑套變形響應面上的最小值，最大變形位置主要分布在循環孔周圍，其余位置變形量較小。

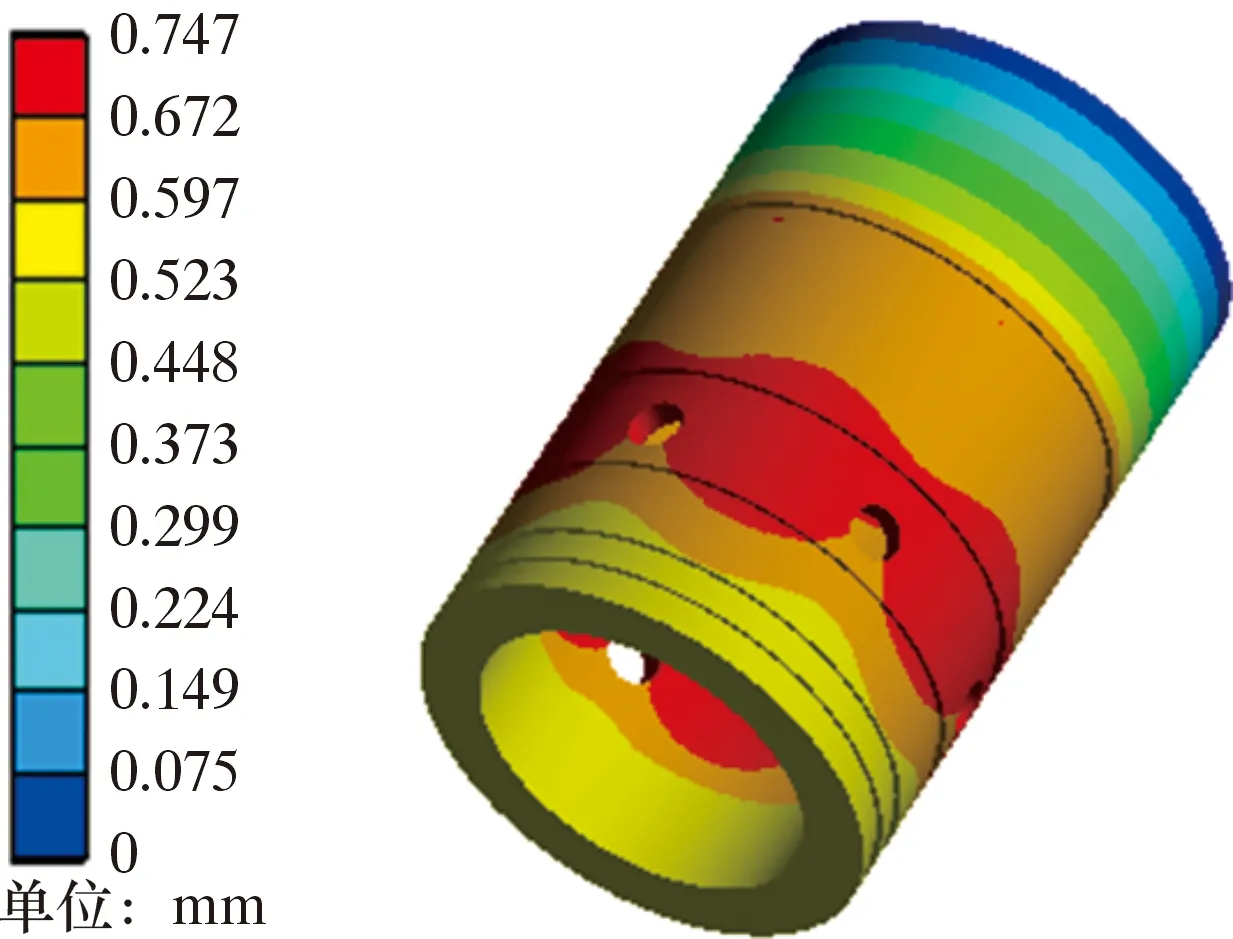
圖14 優化后滑套總變形Fig.14 Post-optimization total deformation of the sliding sleeve

圖15為優化后本體在管內水泥漿自重、套管質量及環空內流體壓力共同作用下的變形云圖。由圖15可以看出，最大變形量為1.658 mm，最大變形主要發生在下接頭位置。

圖15 優化后本體總變形Fig.15 Post-optimization total deformation of the stage casing body

圖16為本體優化后的徑向變形云圖。由圖16可知，最大變形量為0.233 mm，最大變形位置主要位于循環孔周圍及本體內安裝剪切銷釘的位置。

圖16 優化后本體徑向變形Fig.16 Post-optimization radial deformation of the main casing collar

表10為分級注水泥器滑套與本體優化前、后各項性能對比。從表10可見：優化前后滑套的總變形量減少了47.3%，滑套質量增加了7.01%；優化前后本體的總變形量減少了32%，本體徑向變形量減少了62.7%，質量增加了18.6%。

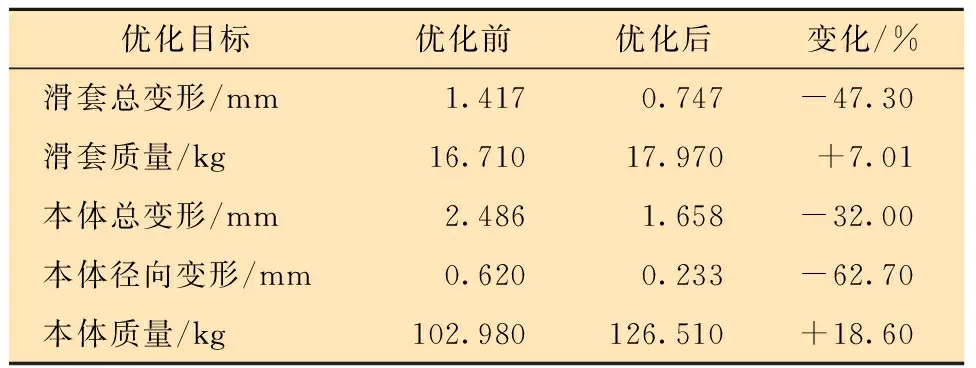
表10 優化前、后性能對比Table 10 Comparison of pre-and post-optimization cases

5 結 論

(1)通過熱流固耦合分析，找出分級注水泥器本體和滑套在高溫高壓流體作用下產生變形量最大的部位。采用拉丁超立方試驗設計法設計了試驗組，并根據試驗組計算結果擬合出滑套最大變形量及質量，本體總變形、徑向變形和質量的響應曲面。

(2)根據擬合的響應面，通過多目標遺傳算法預測出滑套和本體設計變量的最優參數組合，并利用該參數組合構建相應的分級注水泥器優化模型。分別對滑套及本體進行熱流固耦合分析，優化后滑套最大變形量減少了47.3%，本體最大總變形量減少了32%，本體最大徑向變形量減少了62.7%。有效地提高了滑套與本體的剛度和安全性。