惠斯登電橋靈敏度測量方法中的兩個問題

閆夙，張馨月，周毅，劉書妍，王麗

惠斯登電橋測電阻是電磁學實驗中一個重要且典型的基礎性實驗［1?2］，作為一種測量中值電阻的普適方法，提高其測量精確度是非常重要的，所以電橋的靈敏度S是一個重要指標.S的大小與電源的電動勢、四個臂的搭配和橋路電阻的大小都有關系.例如王金輝等［3］討論了恒流源作為電源的惠斯登電橋的靈敏度，發現S與恒流源輸出電流成正比，并且橋臂電阻比例越小，S越大；同時，林麗梅等［4］通過對電壓法和電流法惠斯登電橋測電阻實驗的研究發現，S的大小與橋臂電阻密切相關，并且提出了最佳橋臂電阻的計算公式，從而為電橋的精準測量提供了方便，于華等［5］還發現，當固定比例臂的倍率時，兩個比例臂上的電阻值與待測電阻具有相同數量級時，電橋的靈敏度具有最大值.

此外，S的大小還與電路中檢流計的靈敏度Sg和內阻Rg有關.例如張學華等［6］推導了S的理論公式，并通過相應的實驗驗證了S與Sg的正比關系，同時發現，當Rg的大小等于電橋路端等效電阻時，S具有最大值.可見，在惠斯登電橋測電阻的實驗中，Sg和Rg是兩個很重要的物理量.根據Sg和Rg的大小，可以更加合理地設計電路中各個比例臂上電阻的大小，從而提高電橋的靈敏度.但是，在實驗過程中，學生經常會發現運用檢流計說明書中的Sg和Rg計算出來的電橋靈敏度理論值與實驗值有較大誤差，這應該是由于檢流計使用時間過長使其Sg和Rg不準確造成的，給實驗的設計造成了極大的誤差.

在物理實驗教材中，S定義為電橋平衡時，當一臂的電阻為R，其改變一微小量ΔR后，引起檢流計偏轉Δn格，則S的大小為：

武松安等［7］提出采用交換測量法來減小S的測量誤差，但很少有人討論檢流計指針偏轉方向和偏轉格數對S的影響.本文利用Origin 軟件對1/S?Rx實驗數據進行擬合，從而求出了檢流計Sg和Rg的實際值，再通過具體實驗討論檢流計指針偏轉方向和偏轉格數對S的影響.

1 理論

惠斯登電橋測電阻電路如圖1 所示.S的理論公式［8］為：

圖1 惠斯登電橋電路圖

其中：E為電源電動勢.令R0與R1比值為γ，即Rx=γ·R2，上式可寫成

對其取倒數，得

其中，系數A、B和C分別為：

令y=1和x=Rx，則式（4）寫為：

其中：f1(x)=Ax+C，f2(x)=.所以y=f(x)是由一個一次函數和一個反比例函數構成的初等函數，即1/S是Rx的一個初等函數.

從式（8）可以看出，當x取值較小時，f2(x)會有明顯的影響；隨著Rx的增大，f2(x) 的影響將逐漸減小，當Rx達到一定值時，1/S和Rx的關系接近為一次函數.假設Rx的這個值為Rx的臨界值，用Rxc來表示，即當Rx≥Rxc時，1/S近似為Rx的一次函數，而Rxc的大小應該由實驗條件來決定.

2 實驗內容

實驗過程中，使用WYK?302 型直流穩壓電源、AC5?1 型指針式直流檢流計和5 個電阻箱.主要有以下三個實驗內容.

2.1 利用Origin 軟件求檢流計Sg 和Rg

按圖1 連接電路，固定R0的大小，并取γ=1/10，當待測電阻Rx取不同值時，測出電橋的S值.實驗過程中，在電橋平衡的條件下，改變R2，使檢流計指針分別向左和向右偏轉5 小格，根據靈敏度定義，有

2.2 檢流計指針偏轉方向對S 的影響

取E=3 V，R0=200 Ω，R1=2 000 Ω，Rx=50 Ω，在電橋平衡的條件下，改變R2，使檢流計指針分別向左和向右偏轉5 個小格，求出S左、S右和S，并與S理論進行比較.

2.3 檢流計指針偏轉格數對S 的影響

實驗條件同2.2.當電橋電路平衡的條件下，改變R2，使檢流計指針分別向左和向右偏轉3、5 和7 個小格，求出S的實驗值，即S=≈（S左+S右）/2，并與S理論進行比較.

3 結果與討論

圖2（a）給出了當R0=50 Ω、100 Ω 和200 Ω時，1/S?Rx的實驗數據.從圖中可以看到，當R0=50 Ω時，1/S?Rx接近線性關系，表明Rx在25～200 Ω 之間時取值均較大，即此時的Rxc≤25 Ω，從而使得1/S?Rx的關系接近為一次函數（見式（8））.當R0=100 Ω時，隨著Rx的增大，1/S先減小后增大，當Rx在25～50 Ω 之間時，1/S具有最小值.即當Rx小于50 Ω時，1/S?Rx接近反比例關系，而當Rx≥75 Ω時，1/S?Rx為一次函數，由此可以判斷此實驗條件下Rxc≈50 Ω.而當R0=200 Ω時，可以清晰地看出1/S和Rx的函數關系.當Rx≥100 Ω時，1/S?Rx才近似為一次函數，所以此實驗條件下Rxc≈100 Ω.由此可見，在E=3 V 和γ=1/10 的實驗條件下，R0=50 Ω、100 Ω 和200 Ω時，Rxc的大小分別為25 Ω、50 Ω 和100 Ω，即Rxc隨著R0的增大而增大.此外，從圖2（a）還可以看到，當Rx一定時，1/S隨著R0的增大而增大，即S隨著R0的增大而減小，這也驗證了公式（3）的結論.

圖2 電橋靈敏度測試結果

對三組數據按照式（8）進行擬合，得到的系數和R0、Sg和Rg的計算值見表1，從表中可以看到，當R0=50 Ω 和100 Ω時，R0擬合的大小分別為67.97 Ω 和82.10 Ω，與實驗的真實值（50 Ω 和100 Ω）明顯不相符合，所以相對應的Sg和Rg值不 可取.而當R0=200 Ω時，得到的R0擬合=196.44 Ω，與實驗的真實值（200 Ω）十分接近，所以此時得到的Sg和Rg具有可信性，即實驗中所用檢流計的靈敏度和內阻分別為2.27×105div/A 和196.44 Ω.此外，擬合獲得的Rg=196.44 Ω 與萬用表測量出檢流計的內阻（196.9 Ω）也基本一致，進一步說明了R0=200 Ω 這組擬合數據的正確性.由此可見，在對1/S?Rx的實驗數據擬合求Sg和Rg的實驗中，Rx和R0的取值不能是任意的，要根據R0的大小來設計Rx的取值范圍.由圖2（a）可見，當Rx在25～200 Ω 之間時，只有R0=200 Ω的實驗曲線反映出1/S?Rx的復合函數關系，所以其擬合得到的參數才是準確的.而當R0=100 Ω時，Rx應該在較小值的范圍內取值才會通過數據擬合得到準確的數值.

表1 擬合曲線的主要參數和R0、Sg 和Rg 的計算值

圖2（b）給出了E=3 V、R0=200 Ω、R1=2 000 Ω 時S的理論值與實驗值隨著Rx的變化曲線.其中，理論值為將Sg=2.27×105div/A、Rg=196.44 Ω 代入式（3）求得.可以看到，隨著Rx的增大，S先增大后減小，當Rx=50 Ω時，S具有最大值，約為171.63.所以采用該實驗條件下的惠斯登電橋去測量50 Ω 左右的待測電阻時，電橋才具有最高的靈敏度，實驗誤差最小，測量值越接近真實值；而當待測電阻較大（例如200 Ω）時，電橋的靈敏度會減小，從而增大實驗誤差.所以在運用惠斯登電橋測電阻值時，要根據待測電阻的大小合理地設計實驗條件.此外，電橋靈敏度的實驗值與理論值符合得很好，說明由R0=200 Ω 的實驗數據擬合得到的Sg和Rg較準確.

表2 給出了E=3 V、R0=200 Ω、R1=2 000 Ω、Rx=50 Ω、n=5 div，檢流計左右偏轉時的電橋靈敏度的實驗值，以及相對誤差Δ=（|S理?S|/S理）×100%.將此時的實驗條件（E=3 V，R0=200 Ω，R1=2 000 Ω，Rx=50 Ω）和Sg=2.27×105div/A，Rg=196.44 Ω 帶入公式（3），得此實驗條件下S理論=171.16.從表2 中可以看到，當僅考慮左偏時，ΔR2左的平均值為14.3 Ω，由公式（9）得S左=174.57，相對誤差為1.92%；而當僅考慮右偏時，ΔR2右的平均值為14.8 Ω，S右=168.56，相對誤差為1.52%.S左與S右并不相等，這應該是由于檢流計的零點不準造成系統誤差.在本實驗中，S左總是大于S右，說明此檢流計的實際零點應該在標定零點的左邊.所以在測量惠斯登電橋靈敏度的實驗中，可以通過考慮檢流計偏轉方向來消除檢流計的零點不準造成的系統誤差.表2 第7 列便給出了考慮左右偏轉后，有S≈（S左+S右）/2=171.63，與理論值十分接近，相對誤差僅為0.27%.

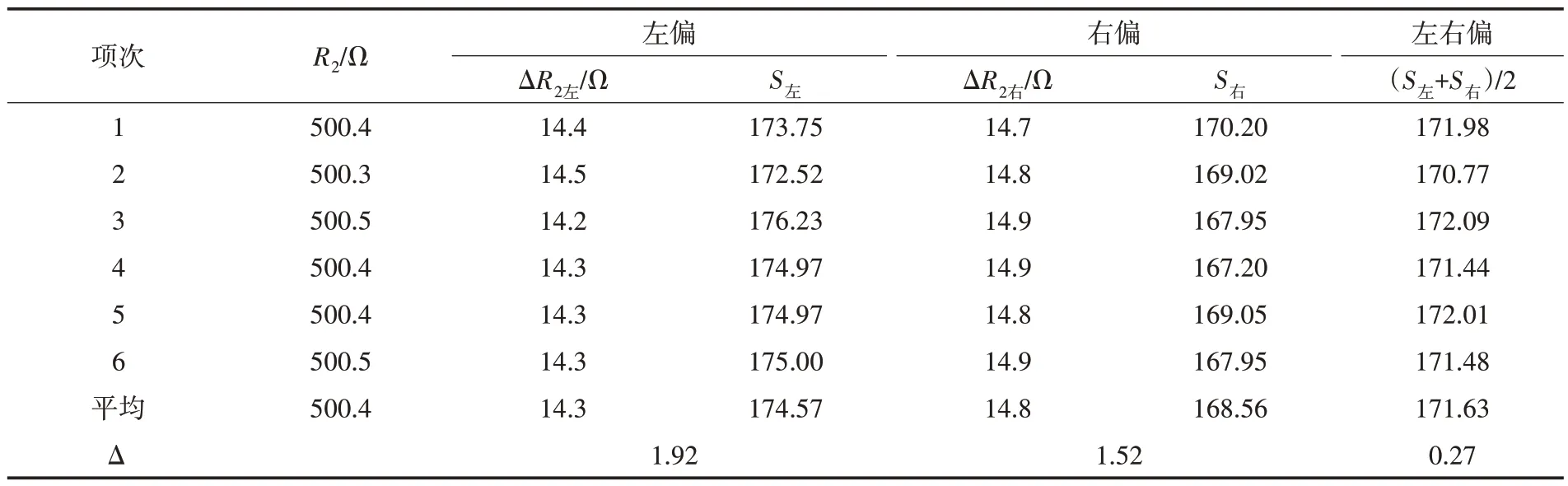
表2 E=3 V，R0=200 Ω，R1=2 000 Ω，Rx=50 Ω，n=5 div時，檢流計左、右偏的S 和Δ

表3 給出了E=3 V，R0=200 Ω，R1=2 000 Ω，Rx=50 Ω，n=3 div、5 div 和7 div時，S的實驗值和相應Δ 大小.從表中可以看到，當n=3 div、5 div 和7 div時，S先減小后增大，與理論值的相對誤差也是先減小后增大.當n=5 div時，電橋靈敏度的實驗值為171.54，與理論值相對誤差最小，約為0.22%.偏轉格數過小，實驗誤差較大，這應該是由于偏轉格數太少，實驗操作不易控制造成的；而偏轉格數較大時，雖然實驗現象明顯，但會增加調節平衡的時間以及數據讀取的偶然性誤差，從而降低了穩定性和重復性.

表3 E=3 V，R0=200 Ω，R1=2 000 Ω，Rx=50 Ω，n=3 div、5 div 和7 div 時的S 和Δ

4 結論

綜上所述，本文在利用Origin 軟件求出檢流計的Sg和Rg之后，研究了檢流計指針偏轉方向和偏轉格數對惠斯登電橋靈敏度測量的影響.結果發現，考慮檢流計指針偏轉方向后，可以有效地消除檢流計引起的系統誤差，從而使實驗值與理論值更加符合.而檢流計指針的偏轉格數對電橋靈敏度的測量也具有一定的影響，當偏轉格數增加時，實驗誤差先減小后增大，當n=5 div時，相對誤差最小.此外，在對1/S?Rx的實驗數據擬合時，要根據R0的大小來設計Rx的取值范圍.希望通過以上研究可以幫助學生更好地理解惠斯登電橋的電路特征，以及測量電橋靈敏度的實驗方法.