基于NSGA-II算法的汽車后背門內板拉延成形質量控制與預測＊

陶哲 季寧

（①天津市靜海區統計局，天津 301600；②天津仁愛學院機械工程學院，天津 301636；③天津大學內燃機燃燒學國家重點實驗室，天津 300072）

汽車覆蓋件因其結構尺寸大、材料薄、形狀復雜且多為空間立體曲面，沖壓時極易出現起皺、開裂等缺陷，影響產品質量。工程實踐中，上述缺陷的產生大多與沖壓工藝參數的設置不當有關。研究表明，沖壓工藝參數對成形質量的影響呈現非線性特征，使得沖壓工藝人員很難直接獲取滿足成形質量要求的沖壓工藝參數[1-3]。目前，常規做法是工藝人員依據根據產品特征憑借自身經驗反復調整工藝參數進行試沖，此種方法不但具有一定的盲目性同時對不同的產品其普適性較差，造成試模時間延長的同時還造成了板材的浪費，增加了企業生產成本。

為減少試模次數，目前大多數汽車零部件廠應用板料成形CAE分析軟件對產品沖壓成形過程進行模擬，預判成形過程中可能出現的影響產品質量的缺陷[4]。但在應用CAE分析軟件時，其工藝參數設置依然是憑經驗設定。對于汽車覆蓋件，因其產品尺寸較大，CAE分析時會有大量的有限元網格參與計算，造成一次分析時間過長，加之為獲得無成形缺陷的工藝參數，需要對工藝參數進行反復修改并進行多次分析，造成分析效率低下。單一地借助CAE分析雖能從一定程度上減少對板材的浪費，依然沒有從根本上擺脫工藝參數設置的盲目性，無法有效縮短獲得合理工藝參數的時間，試模時間縮短有限。

針對上述問題，提出融合CAE分析、響應面模型構建、NSGA-II算法尋優的工藝參數快速優選方法。

通過CAE分析結合拉丁超立方試驗設計方法建立分析樣本進而構建沖壓工藝參數同成形質量之間的響應面模型以擬合二者之間的非線性關系，基于NSGA-II算法在響應面模型內進行工藝參數尋優計算以獲得滿足成形質量要求的工藝參數，并通過實際沖壓試驗對本文提出方法的有效性進行驗證，以期用于指導汽車覆蓋件的生產。

1 產品工藝性分析及有限元模型建立

1.1 產品工藝性分析

本文研究對象為某型汽車的后背門內板，如圖1所示。外形尺寸為1 186 mm×638 mm，深245 mm，有形狀各異的大、小、內、外及側孔40個。客戶要求成形后的材料最大減薄率不超20 %，最大增厚率不超6 %，產品不允許有開裂、起皺等成形缺陷且產品表面不能出現凹點、凸點、拉傷和劃痕。產品拉延深度大且圓角過渡區有復雜的小圓角和壓筋結構，成形難度大大增加。

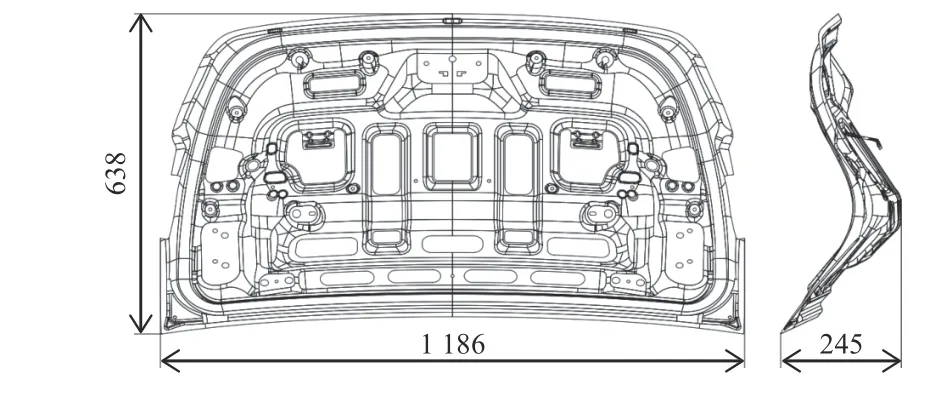
圖1 產品結構圖

產品材質為DC06，材料特性參數見表1所示。

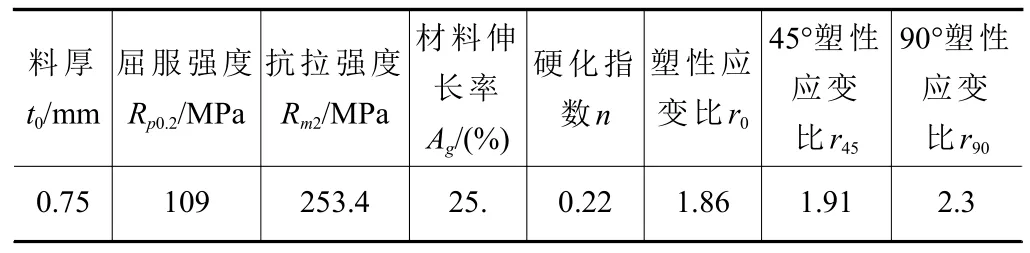
表1 DC06主要性能參數

依據產品結構圖，初步確定該產品沖壓工序為拉延、修邊、沖孔和翻邊。拉延工序最易出現成形缺陷，因此本文主要針對拉延工序進行仿真分析和工藝參數優化，產品模型中的各種孔后續分析均作填充處理。

1.2 有限元模型建立

由于后背門板結構的復雜性，為了保證沖壓過程穩定，需要在制件的外圍增加工藝補充面、壓料面和拉延筋。拉延筋在分模線外20 mm 處設置，拉延筋寬度為15 mm，阻力系數為0.35。最終建立的后背門內板拉延成形的有限元模型如圖2所示。板材在壓邊圈與凹模的作用下沿沖壓方向逐漸與凸模接觸從而拉延成形，當壓力機上滑塊到達下死點時，完成拉延成形過程。

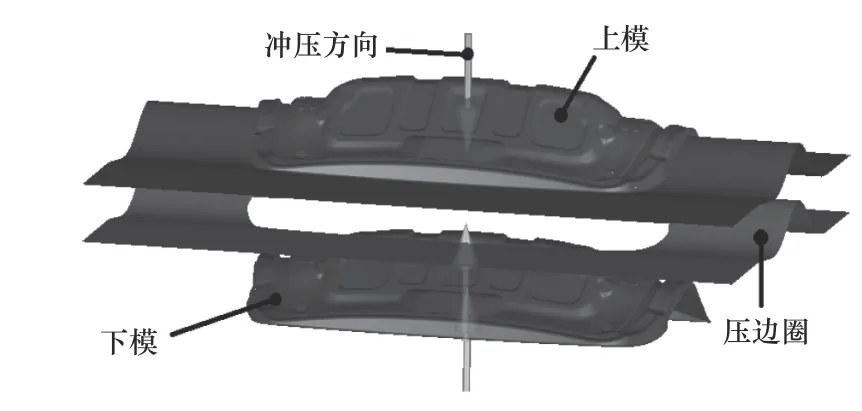
圖2 后背門內板拉延成形有限元模型

2 初始CAE分析

初始CAE分析采用大小為20 mm的自適應三角形網格進行劃分。從圖1可以看出工件結構沿中線左右對稱，為提高分析效率，只分析后背門板右側部分。通過相關計算[5]確定初始工藝參數如下：壓邊力700 kN、摩擦系數0.16、模具間隙0.75 mm、沖壓速度2 000 mm/s。初始分析結果如圖3所示，材料最大減薄率為21.5 %，最大增厚率為8.3 %，兩項成形指標均未達到客戶要求，需對成形工藝參數 進行優化。

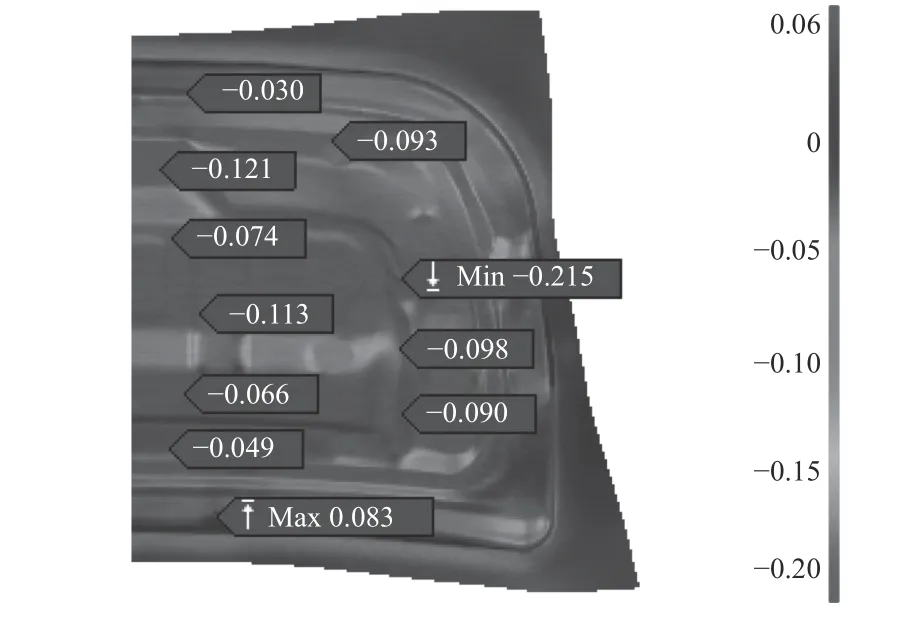
圖3 初始分析拉延成形厚度云圖

3 拉丁超立方試驗設計

拉丁超立方試驗設計（latin hypercube design）避免了正交試驗最優結果只能是試驗所用水平的某種組合的缺陷。拉丁超立方試驗設計的樣本點數量可以人為控制，靈活性較大[6]。其原理是，在n維空間中，將每一維坐標區間[xkmin，xkmax]，k∈[1,n]均勻等分為m個區間，每個小區間記為[xki-1，xki]，i∈[1,m]。隨機選取m個點，保證每一個因子的每個水平只被研究一次，即構成n維空間，樣本數為m的拉丁超立方設計[7]。抽樣樣本點分布示意圖見圖 4所示。

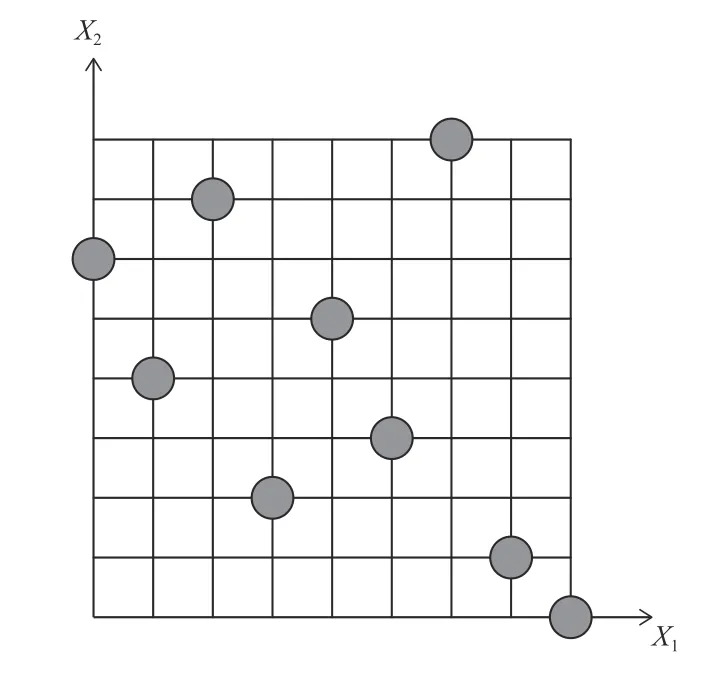
圖4 拉丁超立方抽樣示意圖

為了使拉丁超立方試驗的結果具有實際意義，本文選擇拉深成形時對制件質量影響較大的4個參數，壓邊力（x1）、摩擦系數（x2）、沖壓速度（x3）、模具間隙（x4）作為試驗因素，最大減薄率（y1）和最大增厚率（y2）為優化目標。壓邊圈的壓力必須適當，如果過大，就需要增加拉深力，因而會使工件拉裂，而壓邊圈的壓力過低，就會使工件的邊壁起皺，依據文獻[5]計算過程結合現場沖壓機床性能，壓邊力取值范圍設定為300～800 kN。當采用良好的潤滑油時，摩擦系數可以達到0.05，而比較差的潤滑，摩擦系數可以為0.3，考慮用油成本以及成形要求，摩擦系數取值范圍設定為0.1～0.2。實際沖壓速度與送料機送料速度有關，根據試驗現場條件，確定沖壓速度的試驗取值范圍為1 000～2 000 mm/s。拉深模具凸、凹模具間隙主要依據料厚、壓邊情況及產品精度確定。模具間隙過大，易起皺，產品精度差；間隙過小，摩擦加劇，導致產品嚴重變薄甚至拉裂。生產實際中，拉深模具間隙通常取1.1倍的板料厚度，以此作為參考，最小模具間隙取1倍的板料厚度，最大取1.4倍的板料厚度。綜上論述，試驗因素的水平取值范圍見表2。

表2 試驗因素水平取值范圍

因后續要建立各階響應面模型，建立四階響應面模型時待求系數為23個，因此，依據前述試驗原理并結合Autoform分析軟件，得到23組試驗參數組合下的最大減薄率和最大增厚率，如表3所示，因數據較多，表中只截取部分數據。

4 響應面模型的建立和可靠性驗證

4.1 響應面模型的建立

筆者采用響應面模型擬合沖壓成形質量和沖壓工藝參數之間的非線性關系。響應面模型常用如式（1）所示的數學表達式[8]。

式中：yi(x)為響應目標函數，i為響應面模型階數；xj為第j個試驗因素，j=1，2，···，N；β0為常數項；βj為各項系數；N為待優化工藝參數的數量，N=4。

利用表3中的試驗數據以及式（1）可求出最大減薄率和最大增厚率的各階響應面模型，分別如式（2）～（7）所示，y21(x)、y31(x)、y41(x)分別表示最大減薄率的二階、三階、四階響應面模型函數，y22(x)、y32(x)、y42(x)分別表示最大增厚率的二階、三階、四階響應面模型函數。

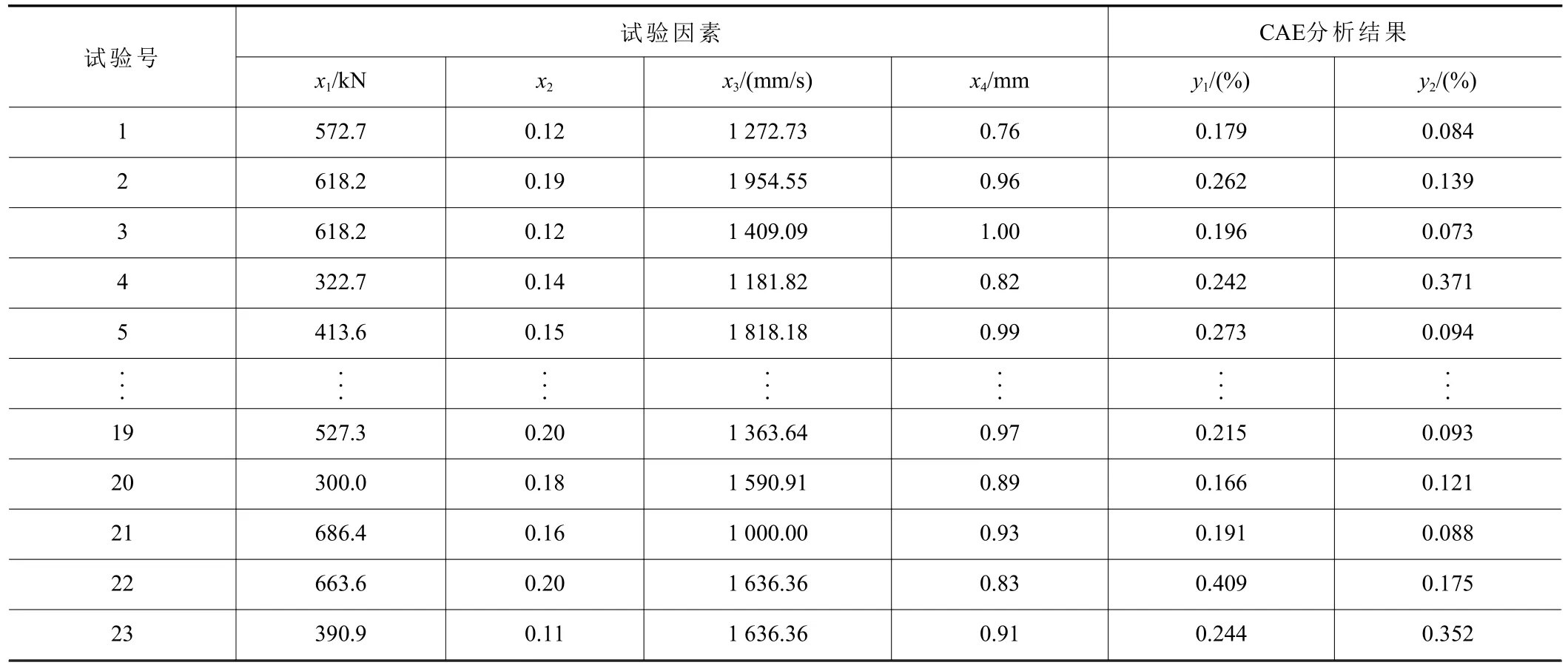
表3 試驗樣本及CAE分析結果

4.2 響應面模型的有效性驗證

為了檢驗代理模型是否能夠準確擬合成形質量同沖壓工藝參數之間的非線性關系，依據表2中數據并應用拉丁超立方試驗設計方法設計的10組檢驗樣本及CAE分析結果，如表4所示。

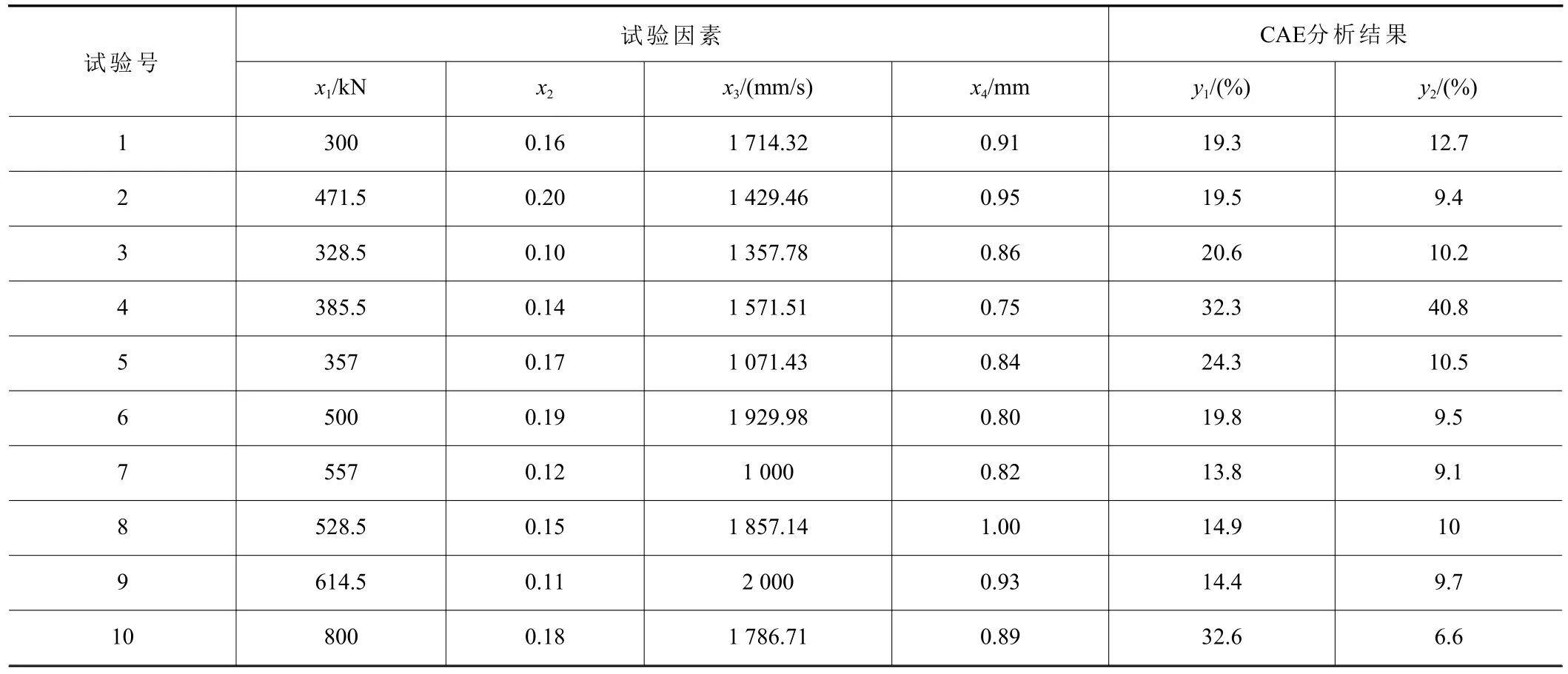
表4 檢驗樣本及CAE分析結果

10組樣本分別代入式（2）、式（4）和式（6）中可以分別計算獲得二階、三階和四階響應面模型對最大減薄率的預測值，預測值與CAE分析值的對比見圖5所示；10組樣本分別代入式（3）、式（5）和式（7）中可以分別計算獲得二階、三階和四階響應面模型對最大增厚率的預測值，預測值與CAE分析值的對比見圖6所示。

從圖5、圖6可以看出四階響應面模型得到的最大減薄率和最大增厚率預測值與CAE分析值更接近。

圖5 預測值與CAE分析值對比

圖6 預測值與CAE分析值對比

工程上常用可決系數R2值或均方根誤差值（RMSE）衡量代理模型的可靠程度。筆者采用式（8）所示的RMSE衡量代理模型的擬合精度。

式中：m為試驗次數；Mi為模型預測值；Ci為CAE分析值；RMSE值越接近于0，說明響應面模型擬合精度越高。

計算可得最大減薄率二階、三階、四階響應面模型的RMSE值，最大增厚率二階、三階、四階響應面模型的RMSE值。計算比較結果見圖7所示。

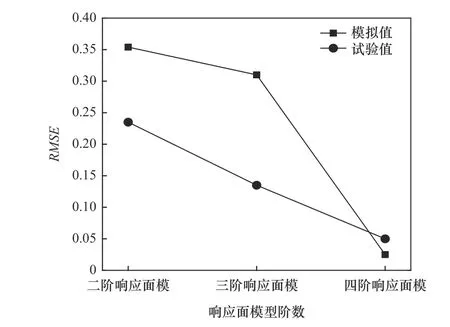
圖7 各階響應面模型RMSE數值比較

從圖7可以看出，四階響應面模型的最大減薄率RMSE值和最大增厚率的RMSE值均小于二階、三階響應面模型所對應的RMSE值且四階響應面模型的RMSE值更接近于0。

綜合以上分析可以得出四階模型的擬合精度最高且滿足分析要求，后續可以通過進行數值計算替代CAE分析進而對最大減薄率和最大增厚率進行預測，可解決CAE分析時間過長帶來的分析效率低下的問題。

5 基于NSGA-II算法的工藝參數尋優

帶精英策略的快速非支配排序遺傳算法（NSGA-II）是一種可對多個目標進行優化的算法。NSGA-II算法[9-11]的程序流程見圖8所示。基于NSGA-II算法在建立的四階響應面模型內尋最優解，算法參數設置見表5所示[12-14]。

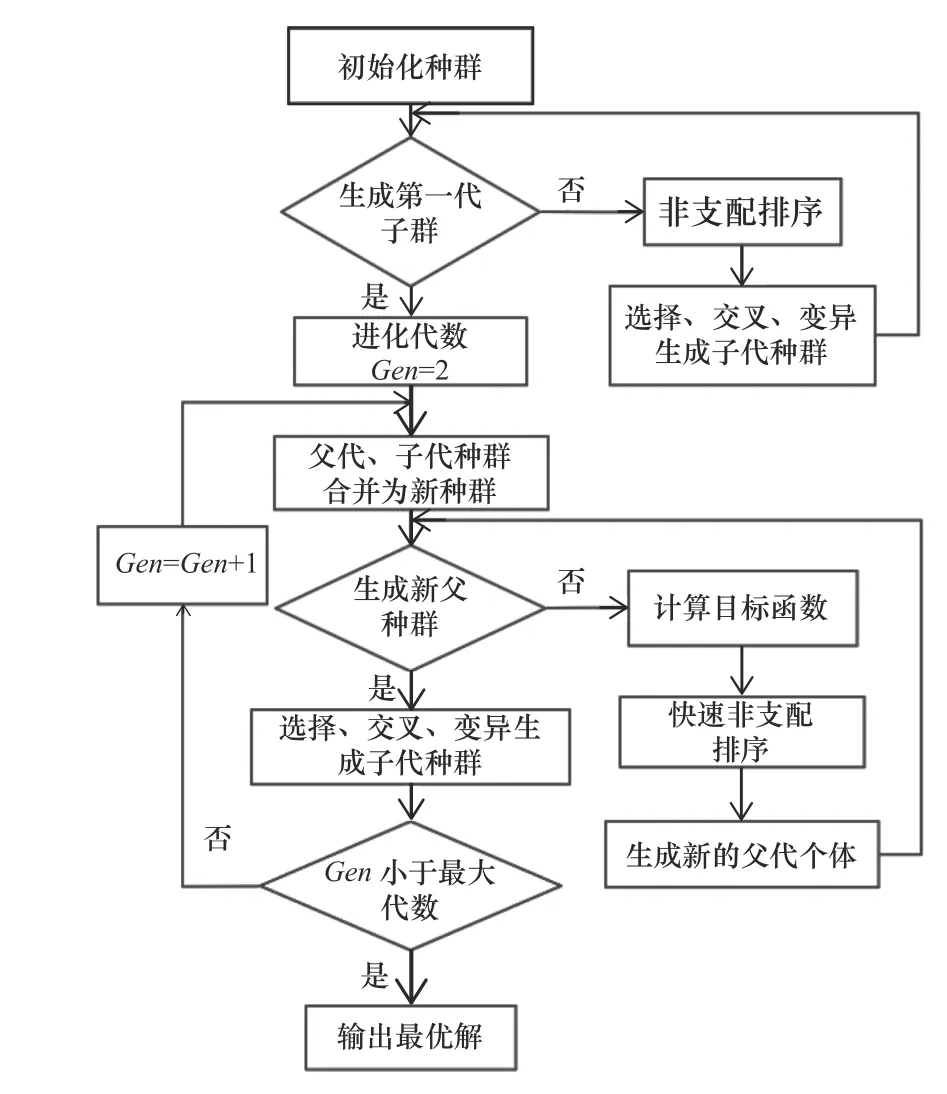
圖8 NSGA-II算法流程圖

表5 NSGA-II算法參數

最大減薄率和最大增厚率無法同時達到最優值，結合表3和表4模擬試驗結果，可以看出，最大增厚率需要在優化計算時設置較大權重。最大減薄率權重配置0.2，最大增厚率權重配置0.8。計算機經過35 s（具體時間視計算機硬件配置），2 400次運算，得到的最優工藝參數如表6所示。算法預測的最大減薄率為18.6%，最大增厚率的預測值為5.1%。

表6 優化后工藝參數

6 試驗驗證

6.1 模擬驗證

在Autoform分析軟件中應用上述得到的最優工藝參數進行分析，成形質量如圖9所示。由圖9可知，CAE分析得到的最大減薄率為19.4 %，與NSGA-II算法尋優得到的最大減薄率預測值18.6 %的相對誤差為4.08 % ；CAE分析得到的最大增厚率為5.6 %，與NSGA-II算法得到的最大增厚率預測值5.1 %的相對誤差為8.9 %；CAE分析結果與NSGA-II算法的預測結果基本吻合，證明了本文提 出的優化方法的有效性。

圖9 優化后拉延成形厚度云圖

與初始CAE分析結果對比，優化后的最大減薄率比優化前的最大減薄率21.5 %降低9.8 %；優化后的最大增厚率比優化前的最大增厚率8.3 %降低32.5 %。二者均取得明顯的優化效果。

6.2 實際沖壓驗證

根據現場條件，將沖壓機壓邊力調整至506 kN，通過調整模面的偏置量以及在模具上涂抹潤滑劑分別保證模具間隙為1.0 mm、摩擦系數為0.17，分別進行拉延、修邊、沖孔及翻邊等工序得到如圖10所示的汽車后背門內板件。

圖10 后背門內板實物圖

利用奧林巴斯超聲測厚儀對拉延后的成形件進行厚度測量并通過計算，得到最大減薄率數值為17.3 %、最大增厚率數值為5.8 %，滿足客戶要求，且與CAE分析結果基本一致，佐證了CAE分析的可靠性。

7 結語

（1）以最大減薄率和最大增厚率為成形控制目標，以壓邊力、摩擦系數、模具間隙和沖壓速度為優化工藝因素，建立了成形控制質量目標同優化工藝因素之間的二階、三階、四階響應面模型。通過數值計算結合CAE分析得出四階響應面模型可靠度最高的結論。

（2）基于NSGA-II算法實現了在四階響應面模型內進行工藝參數的快速優選。對優選后的工藝參數進行CAE分析并與初始CAE分析結果進行對比發現：優化后的最大減薄率比優化前的最大減薄率21.5 %降低了9.8 %；優化后的最大增厚率比優化前的最大增厚率8.3 %降低了32.5 %。

（3）通過CAE模擬和實際沖壓生產驗證了本文所提方法的有效性，為實際沖壓生產中汽車覆蓋件的沖壓成形質量控制與預測提供了一套可借鑒的方法。