大扁平比胎側曲梁分段解析剛度建模及驗證

劉志浩， 馬超群， 劉釔汛， 高欽和， 張博宇， 孟 艷

(1. 火箭軍工程大學 兵器科學與技術軍隊重點實驗室, 西安 710025; 2. 北京航天發射技術研究所， 北京 100076)

重載輪胎作為軍用車輛與地面直接接觸的部件，將絕大多數作用力傳遞至整車，同時還緩解由于路面不平度引起的沖擊與振動，因此輪胎的特性影響整車的動力性[1]、平順性[2]、制動性[3]和操縱穩定性[4]等性能指標。由于輪胎具有極其復雜的結構，具有材料非線性和幾何非線性，因此，如何準確描述胎體、胎側柔性結構振動引起的路面-輪輞振動傳遞特性一直是輪胎動力學研究中的重點和難點。基于結構柔性的輪胎動力學模型[5]，是輪胎結構模型的典型代表，柔性胎體輪胎模型[6]將輪胎簡化成彈性基礎上的柔性胎體，彈性基礎模擬胎側-胎體間作用力和充氣預緊效應。國內外學者研究了不同的胎體柔性化建模方法，提出了從一維到三維的柔性胎體模型，包括基于彈性基礎的弦模型、梁模型、平板模型、環模型、殼模型和分布質量模型等；其中，弦模型和梁模型屬于一維模型，平板模型和環模型屬于二維模型，考慮橫向變形的環模型、殼模型為三維模型。

胎側作為胎體和輪輞的連接和傳力部件，其力學特征和振動特性影響胎體與輪輞間的傳遞特性。國內外學者也提出了一維到三維胎側剛度模型。Zhou等[7]建立了胎側一維徑向剛度的力學特性模型；Liu等[8]建立了考慮胎側慣性質量和分段剛度的一維徑向胎側剛度模型，用以研究柔性胎體與連續胎側曲梁的耦合振動問題。Pacejia[9]首次引入具有徑向和切向剛度的彈簧來表征胎側二維剛度特性；Gong等[10]基于二維彈性基礎的環模型，研究了不同胎側剛度和充氣壓力對輪胎振動特性的影響規律；Liu等[11]建立了考慮圓弧結構彎曲剛度的胎側剛度模型，研究了胎體環與連續胎側環的耦合振動特性。Noga等[12]將胎側剛度由二維拓展至三維，在徑向和切向彈簧的基礎上，考慮了輪胎面外橫向剛度，建立了考慮三維胎側剛度特性的圓環振動模型。

課題組前期以基于彈性基礎的歐拉梁模型[13]為基礎，建立了柔性胎體與胎側耦合振動模型，分析了胎側的分段剛度特性，但缺乏對胎側剛度解析描述，而胎側作為連接柔性胎體和輪輞的關鍵部件，其剛度特性對輪胎的振動特性影響較大，對胎側剛度特性的解析描述變得尤為關鍵。可將胎側等效為圓弧結構，因此胎側的徑向剛度主要體現在兩個方面：① 充氣預緊力作用下的弦剛度，在充氣壓力作用下，在胎側和胎體的連接點處，存在由于充氣預緊力產生的拉伸力；② 胎側結構變形引起的結構剛度，在變形過程中，圓弧單元產生拉伸、剪切和彎曲變形，造成由于胎側結構變形產生的結構剛度。

為完善大扁平比重載輪胎的胎側曲梁分段剛度解析關系，考慮弦預緊效應和結構彎曲特性，推導大扁平比重載輪胎的胎側解析剛度模型，探究胎側曲梁幾何和結構參數的對胎側分段剛度的影響規律；建立重載輪胎胎體-胎側耦合動力學模型，分析胎側幾何和結構參數對輪胎振動特性的影響規律。

1 基于虛功原理的曲梁徑向剛度建模基礎

假定：曲梁為半徑為Rs的圓弧，夾角為2θ，弧長ls，胎體與輪輞間距離為L0，圓弧圓心分別為O1和O2，如圖1所示，存在幾何關系

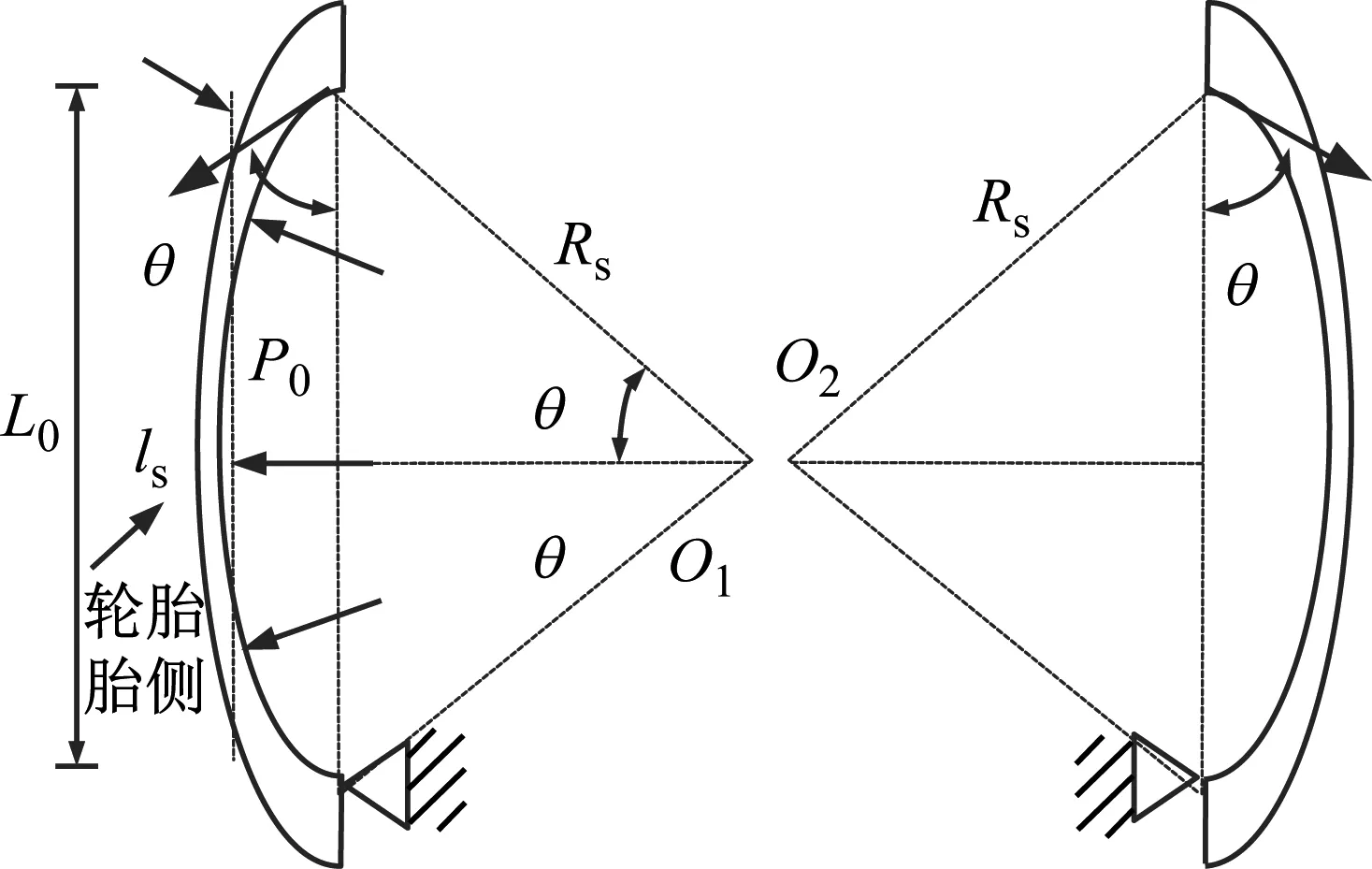
圖1 典型圓弧幾何關系示意圖

(1)

1.1 考慮充氣預緊力的曲梁弦剛度

對單側曲梁進行受力分析，為簡化分析，定義其圓心為O，如圖2所示，建立基于充氣預緊壓力的曲梁弦剛度解析模型。

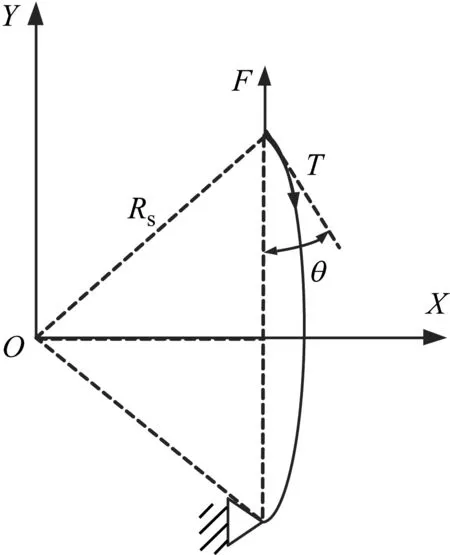
圖2 充氣預緊力作用下的弦效應示意圖

則，由于弦預緊力T=P0Rs(充氣壓力引起的弦預緊力)所引起的沿Y方向的力為

Fs=Tcosθ

(2)

則

Fs=P0Rscosθ

(3)

基于曲梁幾何關系，Fs轉化為

(4)

曲梁沿Y軸長度為

(5)

(6)

則基于充氣預緊力作用的曲梁弦剛度可計算為

(7)

1.2 考慮變形特征的曲梁結構剛度

胎側曲梁除充氣預緊力的弦效應外，其在外力作用下，會產生拉伸力、剪切力和彎曲力矩，因此需將曲梁結構變形考慮在內，如圖3所示。同時在力和力矩的作用下產生響應的結構變形，基于虛功原理，探究曲梁單元在外力作用下產生的彎曲位移ub、拉伸位移ust和剪切位移ush。

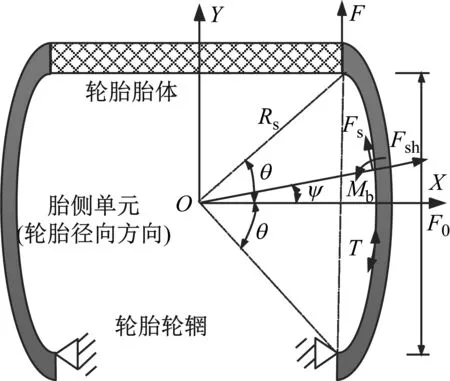
圖3 基于外力作用下的胎側結構變形

在外拉伸力F作用下，胎體任意點處(與X軸夾角為ψ)產生的彎曲力矩Mb，軸向拉伸力Fst和剪切作用力Fsh分別表示為

(8)

則胎側彎曲、拉伸和剪切能Cb，Cst和Csh分別表示為

(9)

基于最小應變能假設，則彎曲力矩Mb作用下產生的變形ub，拉伸作用力Fst作用下產生的變形ust和剪切作用力Fsh作用下產生的變形ush可分別表示為

(10)

將式(8)和式(9)代入式(10)，則外拉伸力作用下產生的胎側結構變形ub,ust和ush可計算為

(11)

則胎側拉伸剛度kst、彎曲剛度kb和剪切剛度ksh可推導為

(12)

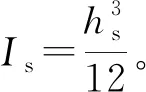
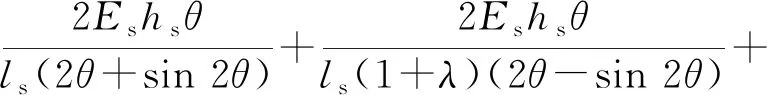
(13)

1.3 基于弦剛度和結構剛度的曲梁解析剛度

曲梁單元解析剛度由結構剛度Ks和弦剛度Kr組成，可表示為

kr=Kr+Ks

(14)

則胎側解析剛度kr可表示為

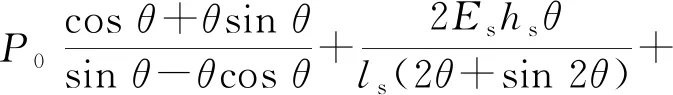
(15)

2 重載輪胎胎體-胎側耦合動力學建模

等效連續胎側梁模擬胎側單元間的彎曲剛度，胎體微段與胎側微段通過胎側上曲梁單元連接，胎側微段與輪輞通過胎側下曲梁單元連接，則對重載輪胎的面內振動特性的研究轉化為基于彈性連續梁基礎的柔性梁模型的動力學分析，如圖4所示。

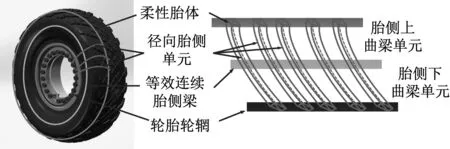
圖4 重載輪胎等效連續胎側梁等效示意圖

2.1 基于彈性連續梁基礎的柔性梁模型動力學建模

對胎體、胎側微段進行受力分析，如圖5所示，ur和usr分別為距原點θ處胎體梁和胎側梁微段截面在時間t時刻的橫向位移。

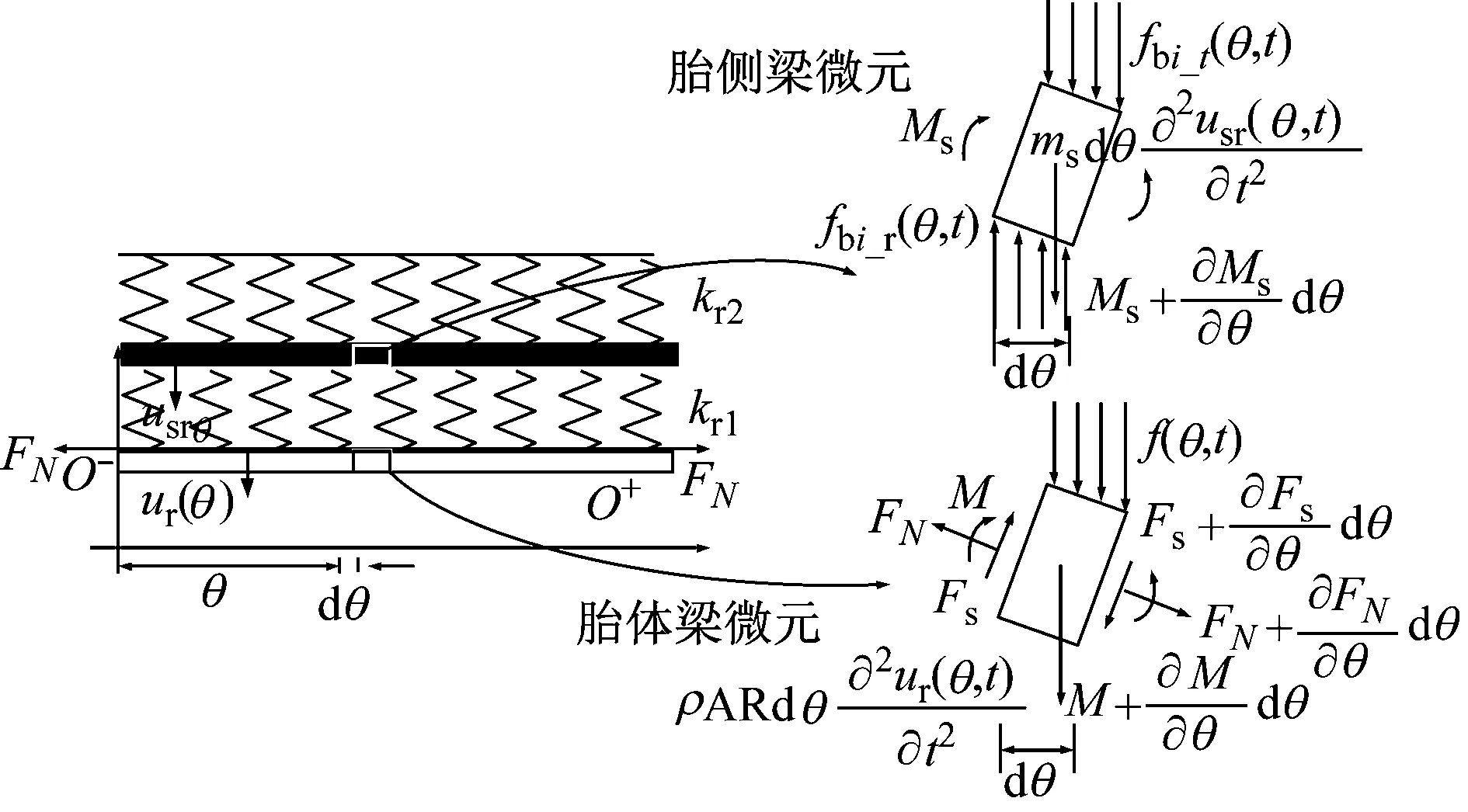
圖5 重載輪胎胎體梁與胎側梁微段受力分析圖

(16)

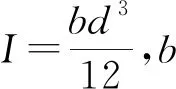
利用泰勒展開對Fs_t和Fs_r進行分析，保留兩項，則胎體-胎側、胎側-輪輞間的作用力轉化為

(17)

(18)

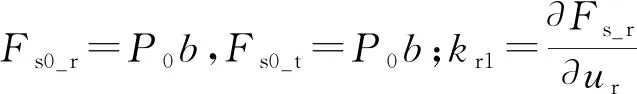
將式(17)和式(18)代入式(16)，則輪輞固定支撐約束條件下的，重載輪胎柔性胎體與連續胎側梁耦合動力學方程為

(19)

2.2 柔性胎體-連續胎側梁耦合動力學求解

利用模態疊加法將胎體-胎側耦合動力學偏微分方程組轉化為空間和時間的常微分方程進行求解，令胎體和胎側的變形ur，usr符合諧波規律，為

(20)

整理，得

(21)

則，式(21)的根為

(22)

其中

重載輪胎柔性胎體-連續胎側梁耦合共振頻率[14]為

(23)

3 大扁平比胎側曲梁解析剛度建模

參照第1章中對大扁平比重載輪胎胎側解析剛度的分析方法，探究圖6中所示的胎側上、下曲梁單元的解析剛度特性，主要包括：① 由于胎側曲率引起的曲梁拉伸、彎曲和剪切變形；② 充氣預緊力效應的胎側膜效應，通過建立胎側曲梁解析剛度式，研究胎側曲梁幾何、結構參數對胎側剛度的影響規律。

針對大扁平比重載輪胎胎側的分段剛度特性，將胎側曲梁等效為上、下胎側曲梁，以胎側曲梁輪廓的最外點A為分段點，如圖6所示。

分別對胎側上、下曲梁的曲梁結構剛度和曲梁預緊力剛度進行分析，而胎側上、下曲梁的總剛度則分別是各自曲梁結構剛度和曲梁預緊力剛度的和。假設：

(1) 胎側徑向曲梁連接輪輞和柔性胎體，點A將胎側曲梁分為上、下胎側曲梁。

(2) 假定胎側為固定曲率圓弧，曲率為1/Rs；O1，O2分別為圖中左、右胎側曲梁的圓弧中心。

(3) 上下胎側曲梁的弧度夾角不同，分別為θc(OB與OA的夾角) 和θw(OC與OA的夾角)，通過對圖6(b)中結構實測，獲得θc=42.5°，θw=60.1°。

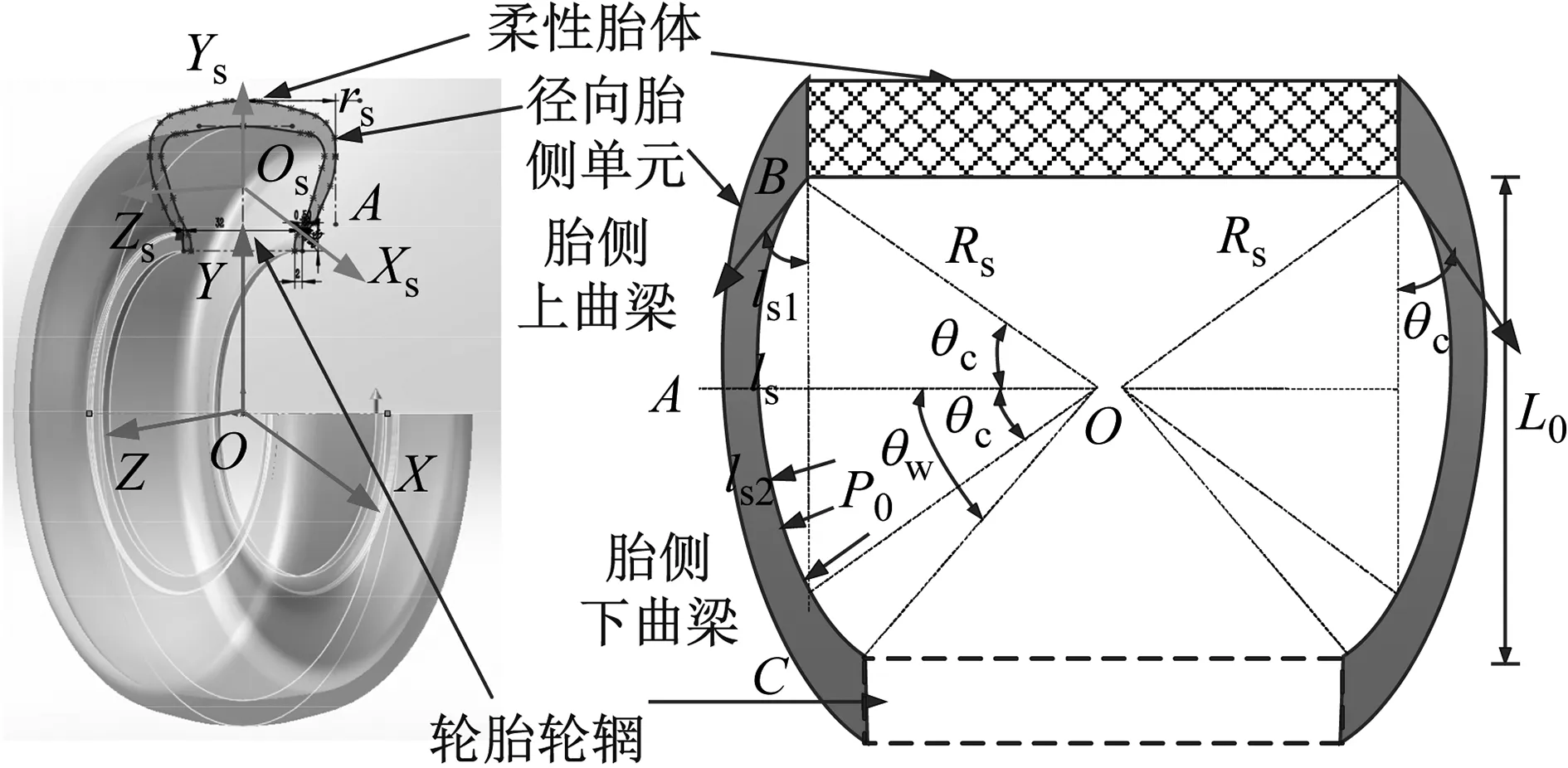
(a) 橫截面結構示意圖

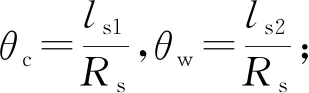
L01=Rssinθc，L01為胎體與胎側點A的Y向垂直距離；L02=Rssinθw，L02為輪輞與胎側點A的Y向垂直距離；L0=L01+L02，其中L0為輪輞與胎體的Y向垂直距離。

3.1 考慮弦預緊效應和結構變形效應的胎側解析剛度建模

上、下胎側曲梁由于充氣壓力弦預緊力引起的徑向力Fsc，Fsw，如圖7所示。其中，T為充氣壓力產生的胎側弦預緊力，T=P0Rs。

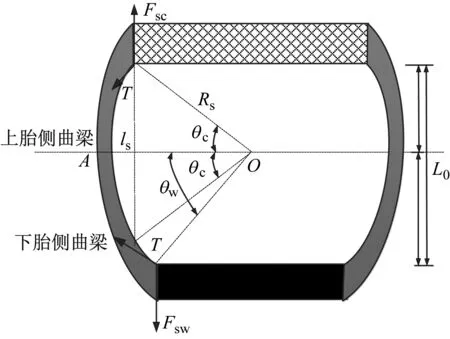
圖7 重載輪胎上/下胎側曲梁弦預緊力

根據胎側幾何結構關系，通過計算胎側弦充氣壓力預緊力T產生的Y方向的垂向力Fsc和Fsw，則上、下胎側曲梁的基于充氣預緊力的弦剛度Kcp和Kwp分別表示為

(24)

式(24)為充氣壓力作用下的胎側弦剛度，此外，外力作用下由于結構剛度引起的胎側變形需考慮在內，包括周向拉伸，彎曲和剪切變形，如圖8所示。以點A為參考點，分別對上、下胎側曲梁的胎側彎曲剛度進行推導，定義：上胎側曲梁與胎體的連接點為B點，下胎側曲梁與輪輞的連接點為C點。

圖8中所示的在點B作用有拉伸力Fsw，同時點C同樣作用有拉伸力Fsw。將胎側曲梁的彎曲、拉伸和剪切變形考慮在內，分別對上、下胎側曲梁基于虛功原理，推導上、下胎側曲梁的結構剛度解析式。

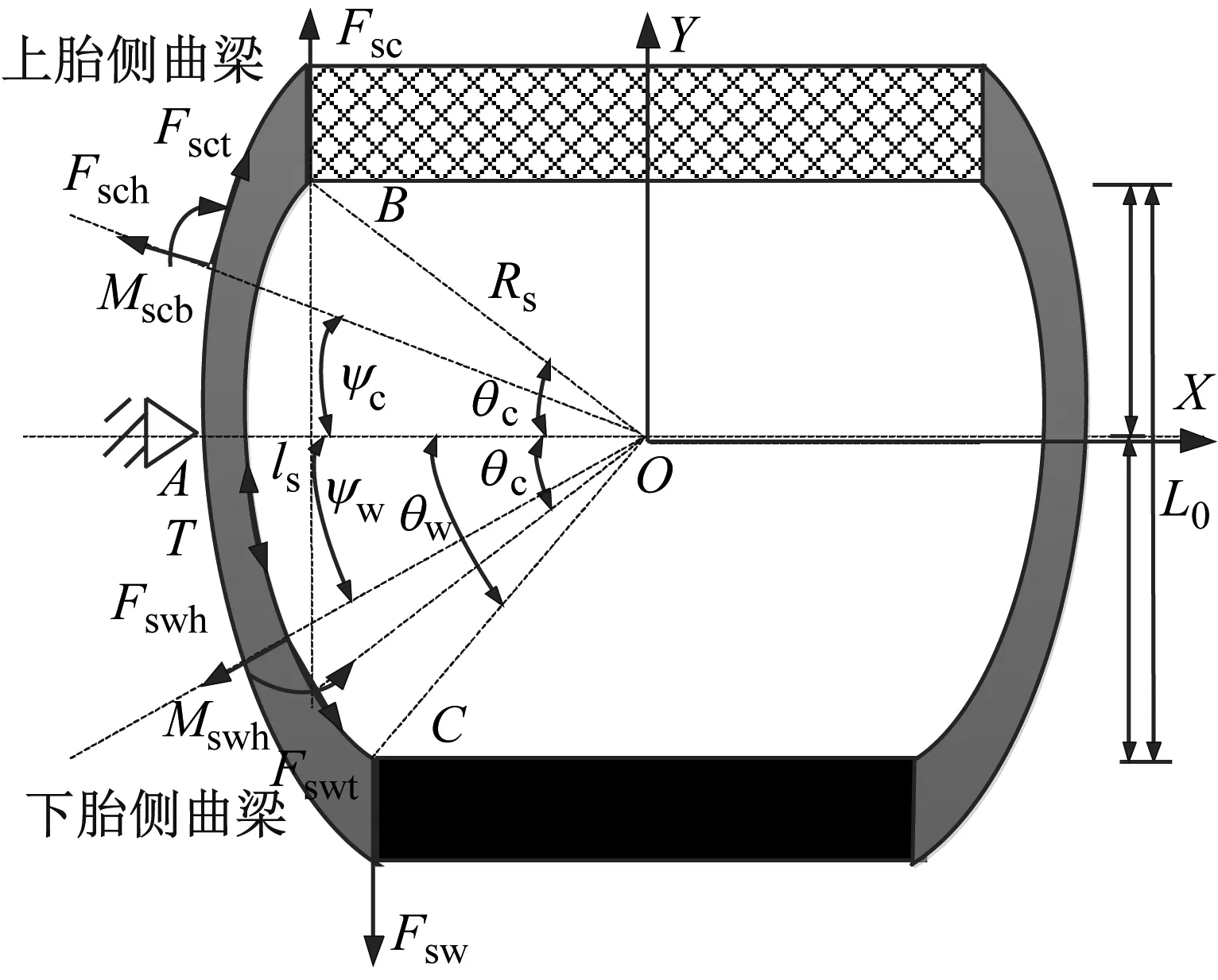
圖8 重載輪胎上/下胎側曲梁的結構變形示意圖

3.1.1 胎體彎曲剛度

基于最小應變能假設，則在外力Fsc和Fsw拉伸作用下產生的上、下胎側曲梁的彎矩Mscb和Mswb所引起的點B，C的變形uscb和uswb可表示為

(25)

推導出

(26)

3.1.2 胎側彎曲剛度

基于最小應變能假設，則在外力Fsc和Fsw拉伸作用下產生的上、下胎側曲梁的端點B和C的變形usct和uswt計算為

(27)

整理得

(28)

3.1.3 胎側剪切剛度

基于最小應變能假設，則在外力Fsc和Fsw拉伸作用下產生的上、下胎側曲梁的剪切力引起的胎體-胎側和胎側-輪輞端點B和C的變形usch和uswh計算為

(29)

整理得

(30)

在外力Fsc和Fsw拉伸作用下產生的上、下胎側曲梁的胎體-胎側和胎側-輪輞端點B和C的結構變形可分別表示為

(31)

(32)

則，上/下胎側曲梁的拉伸剛度ksct/kswt、彎曲剛度kscb/kswb和剪切剛度ksch/kswh為

(33)

(34)

則上/下胎側曲梁的結構剛度Kcs和Kws表示為

(35)

3.2 胎側解析剛度分析及參數辨識

將上、下胎側曲梁的弦預緊效應和結構變形剛度考慮在內，則，上、下胎側曲梁的解析剛度為

(36)

將式(24)和式(35)代入方程式(36)，上/下胎側曲梁的解析剛度分別為

(37)

式(37)表明：

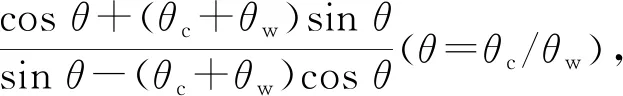
(3) 上、下胎側曲梁的結構剛度與充氣壓力P0無關，與胎側的結構參數包括拉伸剛度EysAys、剪切剛度GysAys和彎曲剛度EysIys。

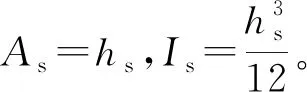
(38)

式(38)中存在兩個未知量Eys和Gys，利用Liu等研究中辨識獲得的上、下胎側曲梁的解析剛度kr1=6.97×106和kr2=3.33×106，采用待定系數法，求解胎側曲梁的彈性模量Eys和剪切模量Gys，結果為Es=1.90×107和Gys=7.58×106，基于計算的胎側結構參數，對上、下胎側曲梁的各剛度組分進行分析，如表1所示。

結果表明：① 式(38)和表1表明，上、下胎側曲梁不同的弧度角是導致上、下胎側曲梁剛度不同的原因，同時上胎側曲梁的結構剛度百分比小于下胎側曲梁的結構剛度百分比；② 上、下胎側曲梁的各項剛度組分中，彎曲剛度遠小于拉伸和剪切剛度，因此，可忽略胎側彎曲剛度對胎側解析剛度的影響；③ 上、下胎側曲梁解析剛度均與胎側結構參數和各自的幾何參數相關，可基于式(38)開展重載輪胎胎側曲梁的解析剛度參數影響分析；④ 考慮胎側結構阻尼的影響，則上、下胎側曲梁的阻尼系數為

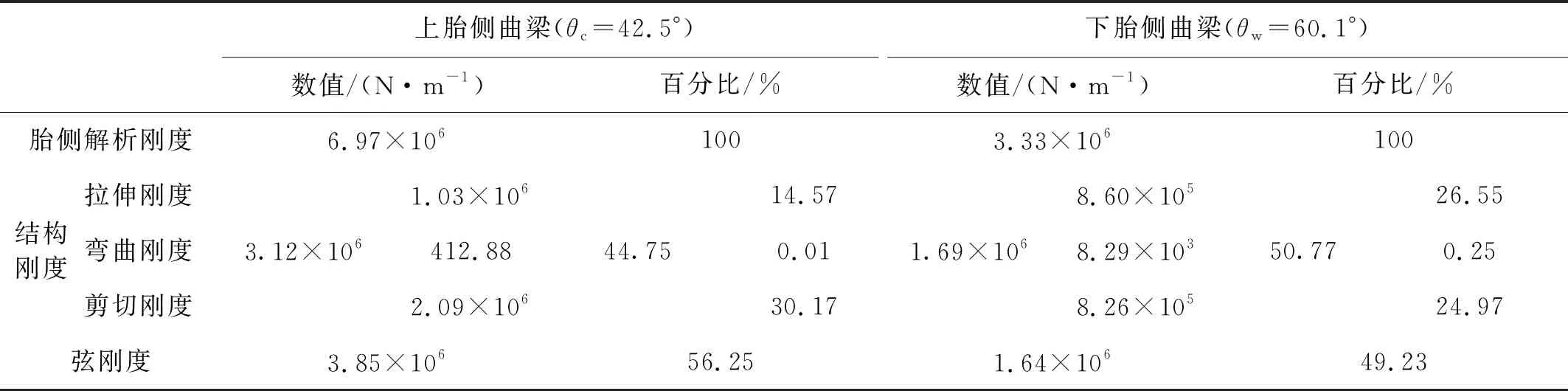
表1 重載輪胎上/下胎側曲梁的弦剛度和結構剛度分析

(39)

4 大扁平比胎側解析剛度參數分析

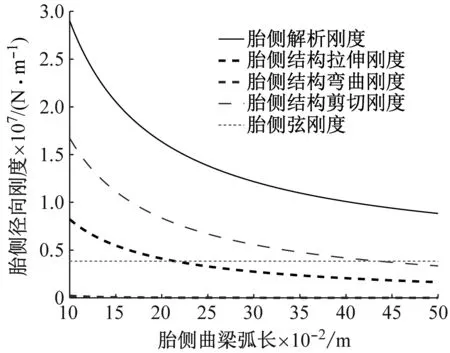
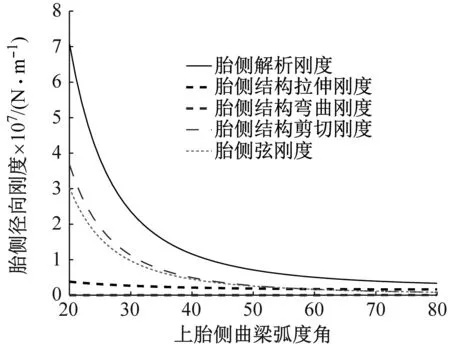
分別對胎側上、下曲梁的結構和幾何參數對胎側曲梁剛度的影響規律和輪胎振動模態特征開展研究，包括：胎側徑向彈性模量Eys、剪切模量Gys、截面厚度、曲梁圓弧長和曲梁弧度角，結果如圖9～圖13所示。結果表明：① 胎側徑向方向彈性模量主要影響胎側拉伸剛度項，見圖9(a)、圖9(b)，彈性模量增大，胎側剛度增大，成近似線性比例增長；② 胎側徑向方向剪切模量主要影響胎側剪切剛度項，見圖10(a)、圖10(b)，剪切模量增大，胎側剛度增大，成近似線性比例增長；③ 胎側截面厚度主要影響胎側結構剛度項，見圖11(a)、圖11(b)，截面厚度越大，胎側剛度增大，成近似線性比例增長；④ 胎側曲梁弧長主要影響胎側結構剛度項，見圖12(a)、圖12(b)，截面弧長越小，胎側剛度增大，成非線性反比例關系；⑤ 圖13為假定上、下胎側弧度角總和不變的條件下，上胎側曲梁弧度角變化時的胎側剛度變化圖，結果表明，弧度角對胎側的弦剛度和結構剛度均有影響，弧度角減小，胎側弦剛度和結構剛度均增大，成非線性反比例關系。

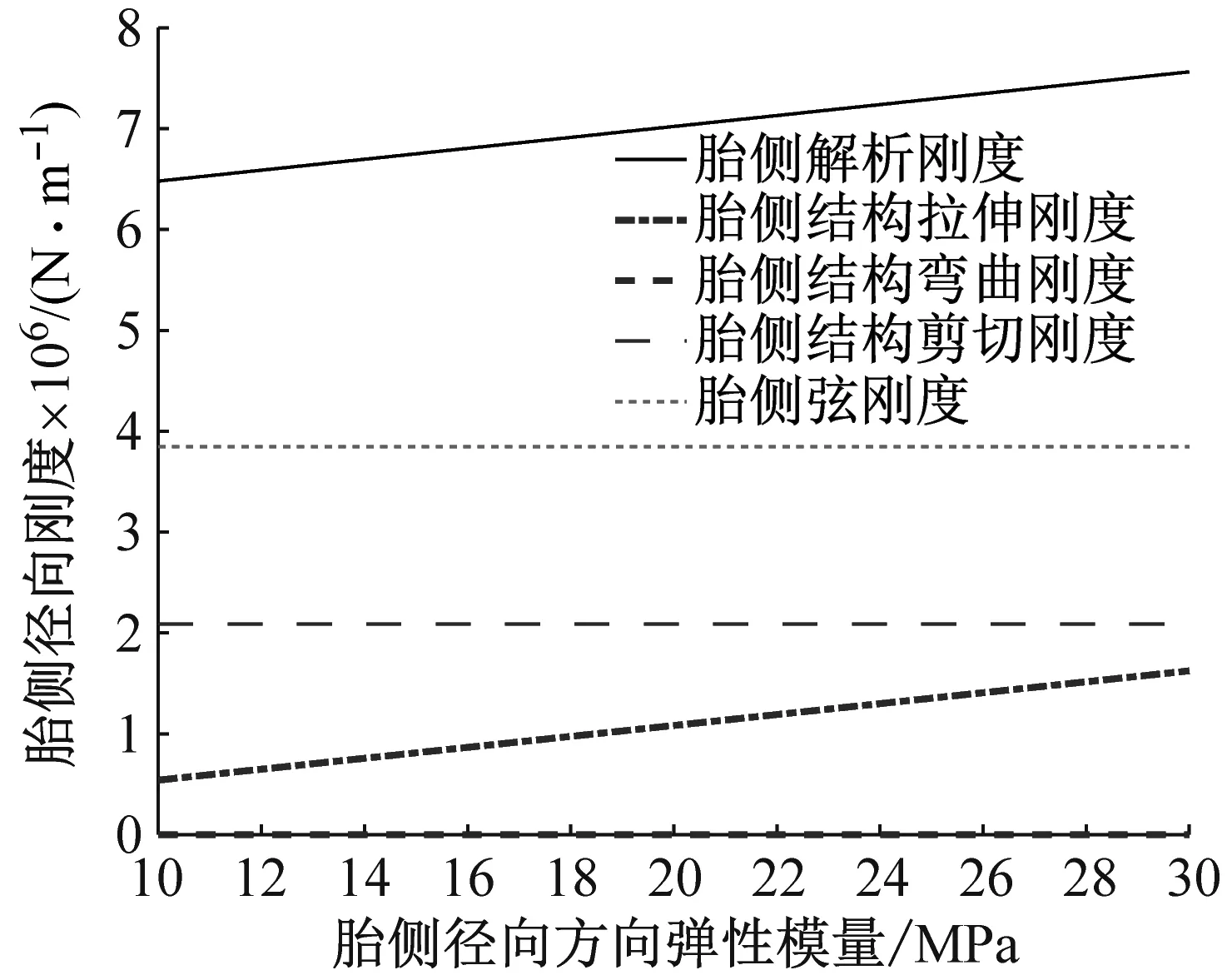
(a) 上胎側曲梁剛度分析

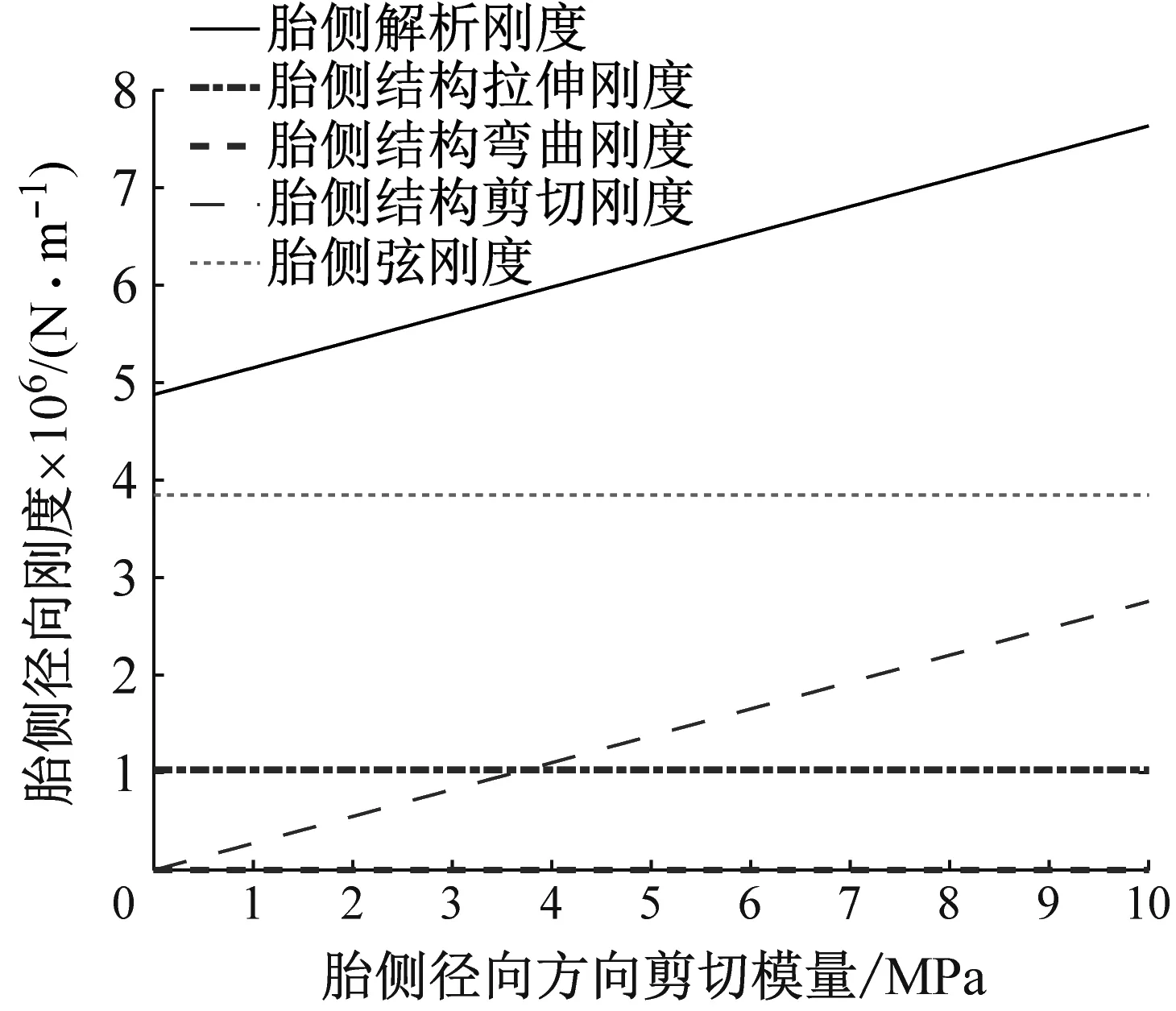
(a) 上胎側曲梁剛度分析

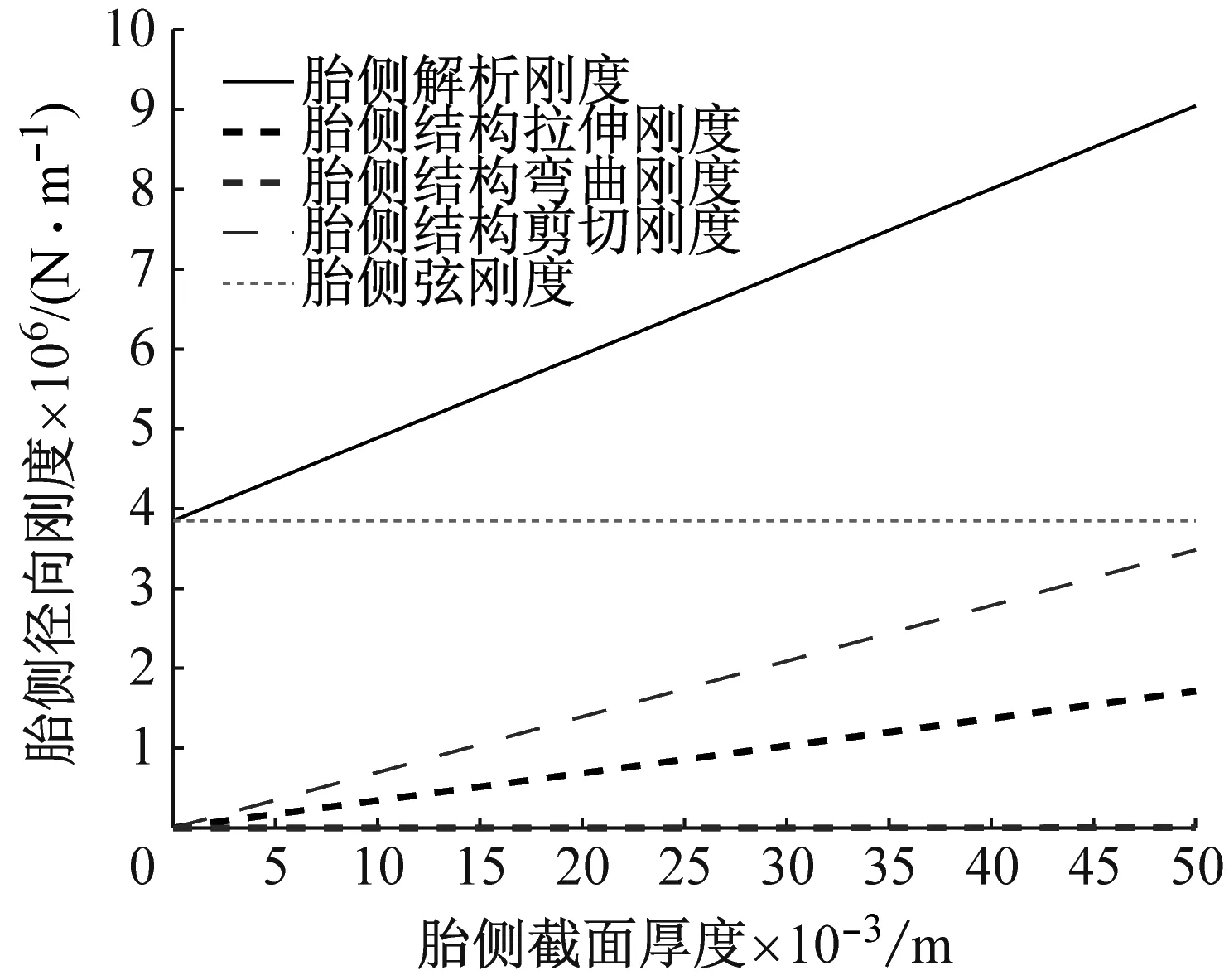
(a) 上胎側曲梁剛度分析

(a) 上胎側曲梁剛度分析

(a) 上胎側曲梁剛度分析

5 胎側曲梁參數對振動特性影響分析

分別對胎側上、下曲梁的結構和幾何參數對胎側曲梁剛度的影響規律和輪胎振動模態特征開展研究，包括：胎側徑向彈性模量Eys、剪切模量Gys、截面厚度、曲梁圓弧長和曲梁弧度角，結果如圖14～圖18所示。

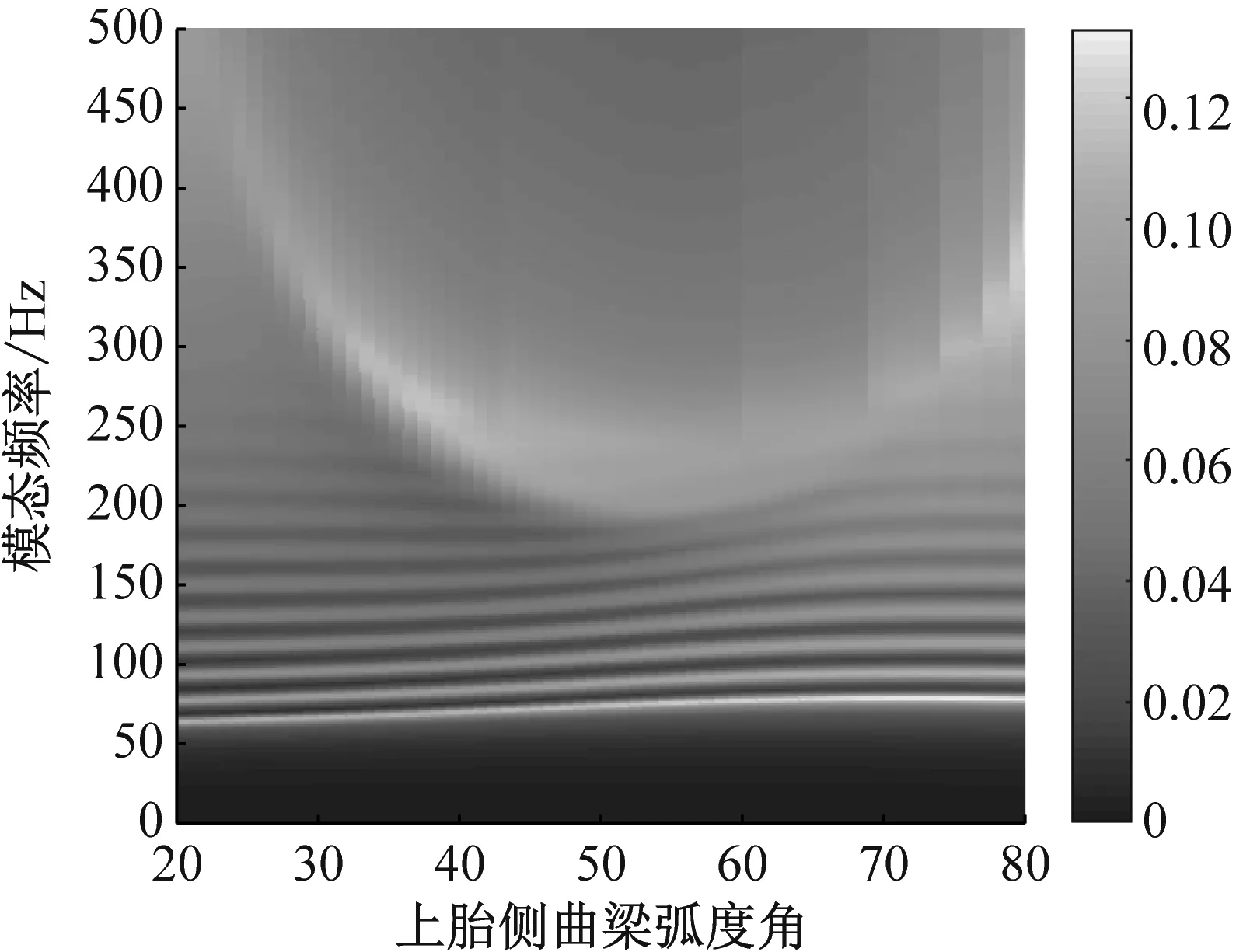
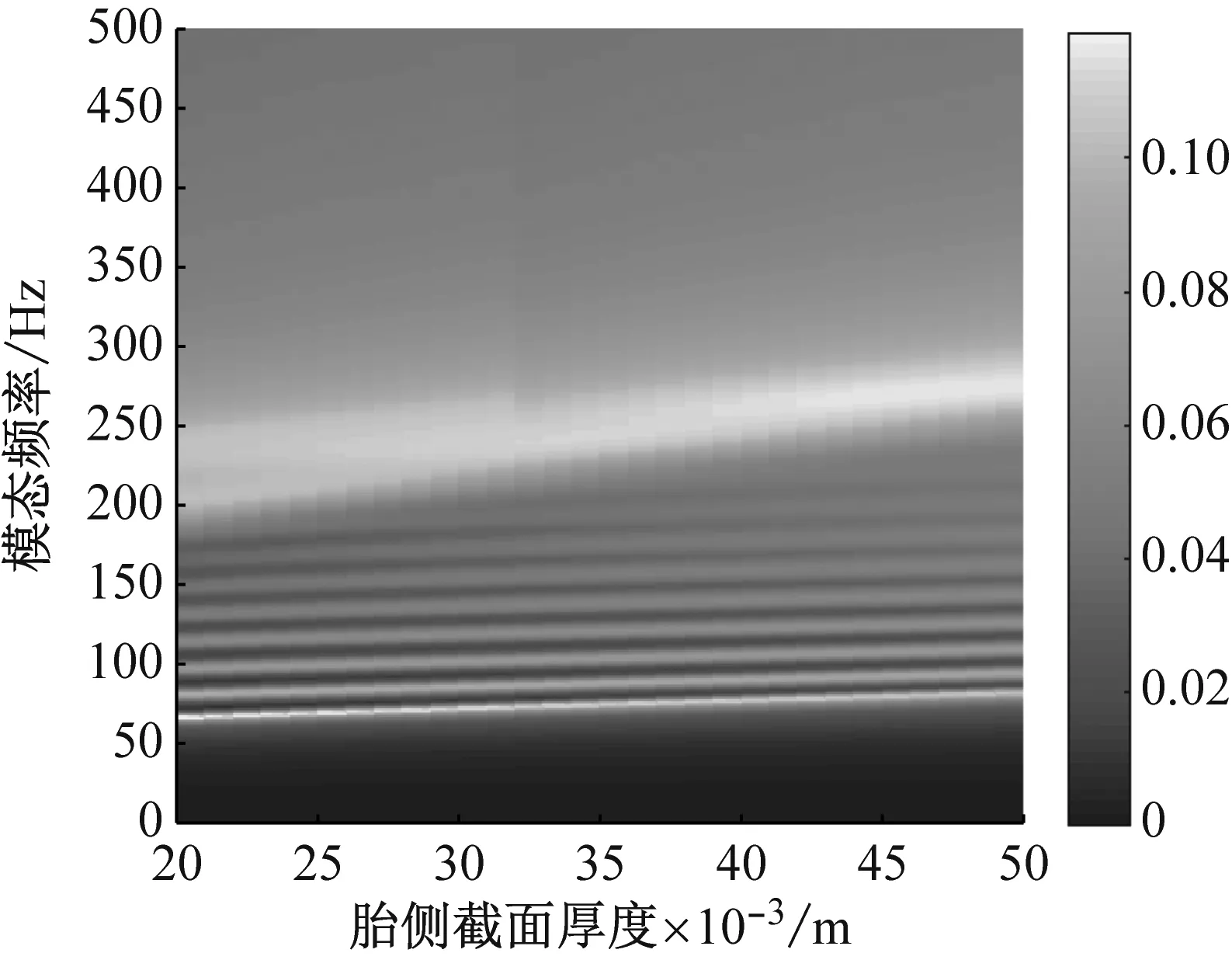
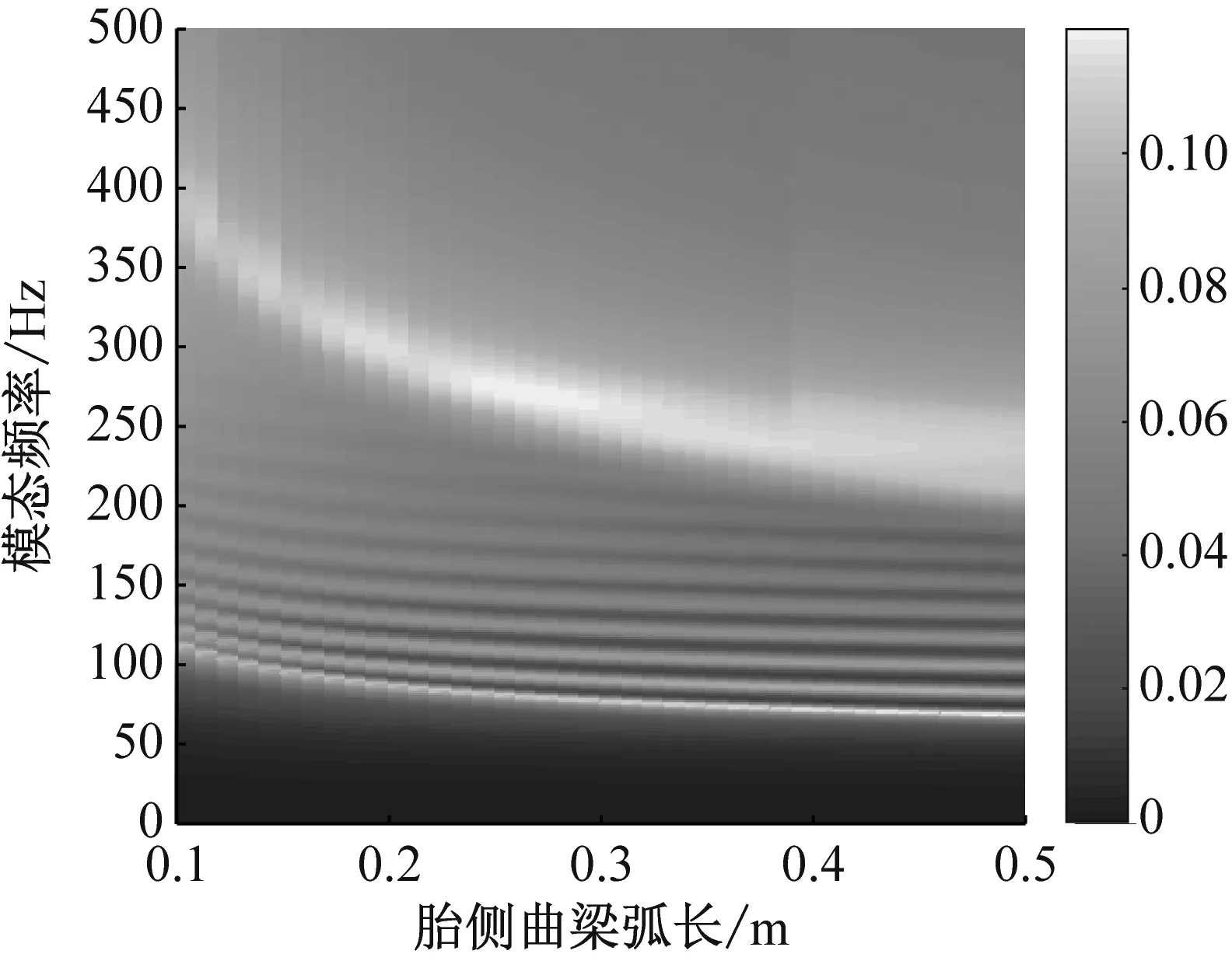
結果表明：① 胎側徑向方向彈性模量增大，胎側剛度增大，成近似線性比例增長，見圖14；② 胎側徑向方向剪切模量增大，胎側剛度增大，成近似線性比例增長，見圖15；③ 圖16為假定上、下胎側弧度角總和不變的條件下，上胎側曲梁弧度角變化時的輪胎振動模態變化圖，結果表明，弧度角減小，胎側弦剛度和結構剛度均增大，成非線性反比例關系，進而改變輪胎的振動模態；④ 相同胎側材料比重的前提下(胎側簾線與胎側橡膠的體積比)，胎側截面厚度越大，胎側剛度增大，成近似線性比例增長，見圖17；⑤ 胎側曲梁弧長越小，胎側剛度增大，成非線性反比例關系，見圖18。

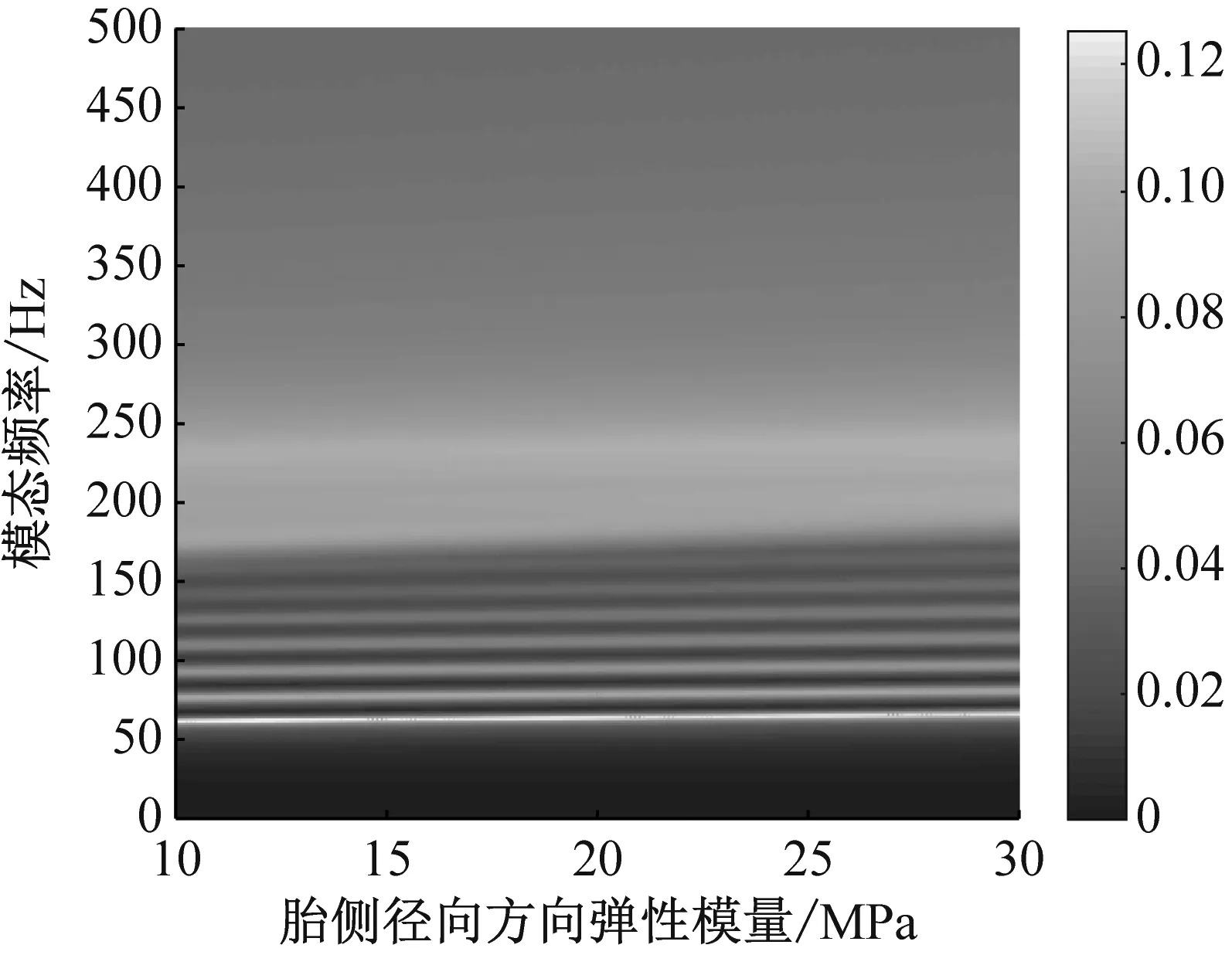
(a) 振動傳遞特性

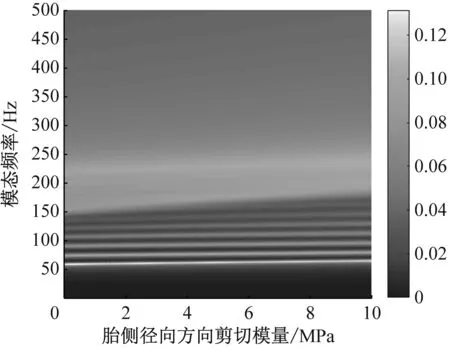
(a) 振動傳遞特性

(a) 振動傳遞特性

(a) 振動傳遞特性

(a) 振動傳遞特性

6 結 論

本文以重載大扁平比輪胎為研究對象，針對其中低頻范圍內的胎體與胎側耦合振動特性，建立了基于連續胎側彈性基礎的柔性胎體輪胎動力學模型，并進行了模態頻率和振動特性推導；針對重載輪胎胎側曲梁的大扁平比的結構特點，考慮弦預緊效應和結構彎曲特性，建立了胎側分段解析剛度模型；并基于該解析分段胎側模型，分析了胎側曲梁幾何和結構參數對胎側分段剛度、輪胎傳遞特性及模態頻率的影響規律。得到以下結論：

(1) 大扁平比胎側曲梁的徑向分段剛度由充氣壓力引起的弦預緊項，及胎側曲梁的拉伸、彎曲和剪切相關的結構剛度項組成。

(2) 胎側曲梁分段剛度與胎側曲梁的幾何、結構和充氣壓力參數直接相關，因此基于胎側曲梁分段解析剛度模型可實現對輪胎模態頻率及傳遞特性優化。