模態截斷對懸索非線性耦合共振響應影響

張昕濤， 趙珧冰， 2， 蔡紹輝， 郭智銳

(1. 華僑大學 土木工程學院， 福建 廈門 361021；2. 福建省智慧基礎設施與監測重點實驗室， 福建 廈門 361021)

非線性動力系統的數學模型，常采用偏微分方程來描述其運動，理論上這類方程可以利用多尺度等攝動法直接求解[1]。然而動力系統均有無窮多階模態，其線性模態具有同頻性、不變形、正交性和疊加性[2]。因此無論是試驗測試還是理論分析，都只能獲得一定數量或者某頻率帶內的模態，無法獲得系統全部模態。因此為研究簡便，僅考慮有限模態，研究人員采用模型降階對各類動力系統進行離散降維[3-4]。那么采用有限模態來描述一個無窮維連續系統的動力學行為，高階模態振型和頻率被忽略，如何評價其結果的收斂性和準確性，是否能真實反應系統非線性振動特性，研究中需要重點關注。

為了使離散導致的誤差盡量降低，模態截斷的數量應盡可能大。然而隨著模態階數不斷增加，計算結果雖趨于穩定，但效率迅速下降，準確度提升卻非常有限[5]。同時部分非線性系統，低階離散模型即可展示其真實動力學特性。因此研究人員截取一定數量的模態，不但可以保證計算結果準確，而且使得消耗的資源可控，便于工程實踐以及理論分析。然而對于各類非線性系統[6-13]：碰撞系統、矩形薄板、風力機葉片、輸液管、懸臂管、黏彈性梁以及懸索等，模態截斷數量差異較大，必須針對性地開展計算和分析。單純的模態分析，很難直接判定模態截斷有多大的影響，只能通過結構動力響應或模態貢獻量，間接判斷模態截斷的影響，得到合理的模態截斷數。倘若進一步涉及到模態間的耦合共振，此時能量會在不同模態間傳遞，導致系統發生大幅振動，危害結構安全，此時如何評價不同模態對耦合共振的貢獻，也是研究人員重點關注的。

在上述眾多非線性動力學系統中，懸索作為一類大跨度柔性結構，其動力學行為豐富且復雜。以懸索面內和面外主共振為例，忽略模態間耦合共振時，Arafat等分析了有效非線性系數與模態截斷階數的關系，通過對比直接法和離散法的近似結果，發現單模態離散可能會導致明顯的定量和定性的誤差。Guo等[14-15]針對可移動邊界問題，進一步對比和分析離散法帶來的誤差并闡述其根源。對于多模態內共振響應，為計算簡便，離散時常常只考慮直接激勵和內共振兩個模態[16]。然而非直接激勵以及非內共振模態對系統共振響應或多或少存在影響[17]，單純僅考慮兩模態離散可能無法準確反饋系統模態間的耦合振動特性。

懸索動力學方程極具代表性，其同時包含立方非線性(由張拉力引起)和平方非線性(由垂度導致)，很多動力系統(斜拉梁、梁-索-梁、淺拱、板、葉片等)離散后均可以表示成類似方程。因此本文基于懸索面內非線性動力學模型，采用Galerkin法進行離散，以系統發生3∶1內共振響應為例進行分析。該形式的內共振與立方非線性項直接相關，該非線性源于懸索的初張力。通過對比兩種模態截斷(九階和兩階)時，系統的激勵響應幅值曲線、幅頻響應曲線、時程曲線、相位圖、頻率譜、龐加萊截面以及李雅普諾夫指數的異同，從而闡述模態截斷對該類動力系統耦合共振響應特性的影響。

1 動力學模型

圖1所示水平懸索，跨度為L，垂度為b，懸掛于O和B。以O為原點，OB為x軸，垂直于OB向下為y軸建立坐標系O-xy。在均布簡諧荷載作用下，u(x,t)和v(x,t)分別為懸索軸向和豎向的位移。

圖1 懸索構形及特性

忽略懸索彎曲、扭轉以及剪切剛度，基于哈密頓變分原理，引入擬靜態拉伸假設，并結合索軸向張力平衡方程，得到懸索軸向應變的擬靜態解。然后積分并引入邊界條件，可得系統軸向的運動方程u(x,t)，從而得到懸索面內非線性運動微分方程

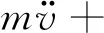
(1)

式中：“·”為對t求導；“′”為對x求導；m和cv分別為懸索單位長度質量和阻尼系數；A為橫截面面積；E為彈性模量；H為初始水平張力；y(x)為靜態構形，拋物線表示為y(x)=4b(L-x)x/L2；Fv和Ω分別為外激勵幅值和頻率。

引入無量綱參數[18]，并代入式(1)，利用Galerkin法進行離散，將空間x和時間t分離，可得離散后的無窮維常微分方程[18]

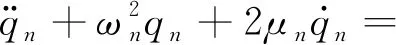
(2)

式中：qn(t)為廣義坐標；模態函數以及系數如Zhao等的研究所示。

2 攝動求解

對于二階常微分方程式(2)，采用多尺度法求解近似解，首先將該二階微分方程改寫為兩個一階方程

(3)

(4)

將上述位移和速度的廣義坐標代入式(3)、式(4)中

(5)

ε2:D0qk2-zk2=-D1qk1,

(6)

ε3:D0qk3-zk3=-D1qk2-D2qk1

D2zk1+fkcos(Ωt)

(7)

假設懸索m和n階模態之間發生內共振，那么一階方程式(5)的解表示為

(8)

式中，δkm和δkn(k=m,n)為Delta函數。將式(8)代入二階方程式(6)，可得二階近似解

zk2=D0qk2

(9)

此處以k=m為例(同理可計算k=n)。將式(8)、式(9)代入三階方程式(7)中第二個方程，可得

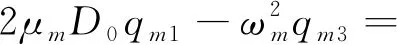
-D1zm2-iωmD2AmeiωmT0+

fmcos(Ωt)+NST

(10)

此時平方非線性導致的共振項可表示為

(11)

式(8)、式(9)中均包含頻率ωk(k=m,n)，而對于由于平方非線性引發的共振項式(11)，其包含一階和二階方程解的乘積項，因此導致內共振響應勢必受到其他非共振模態影響，無法直接忽略。倘若進行兩階模態截斷，其余非共振項和非直接激勵項均被忽略。同時，對立方非線性導致的共振項進行分析，如下所示，由于攝動階數，其不包含二階解

(12)

結合式(10)、式(11)，得式(10)最終表達式

(13)

其中非線性相互作用系數Kij表達式如下

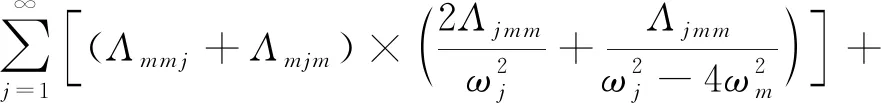
3Γmmmm,

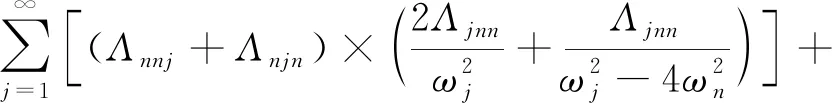
3Γnnnn

(14)

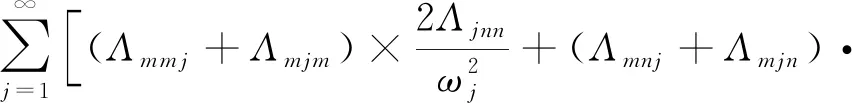
2(Γmnnm+Γmnmn+Γmmnn),

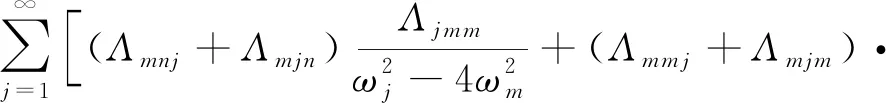
(Γmnmm+Γmmnm+Γmmmn)

(15)

本文假設系統兩正對稱模態之間發生3∶1內共振，為了描述外激勵頻率與模態頻率之間以及兩模態頻率之間差值，引入外調諧參數σ1和內調諧參數σ2：Ω=ωi+εσ1和ωn=3ωm+εσ2，其中：i=m,n。根據式(13)，得到可解性條件，再根據重組法得到調諧方程。此時Aj可表示成極坐標形式和直角坐標形式，為描述簡便，本文采用直角坐標形式：Aj=[pj(t)-irj(t)]·eiβj(t)/2,j=m,n，系統調諧方程如下所示

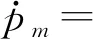
(16)

(17)

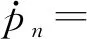
(18)

(19)

式中：當激勵直接作用在低階模態時(Ω=ωm)，υm=σ1，υn=(3σ1-σ2)；當激勵直接作用在高階模態時(Ω=ωn),υm=(σ1+σ2)/3,υn=σ1，式中其他非線性相互作用系數為(S=Sm=3Sn)

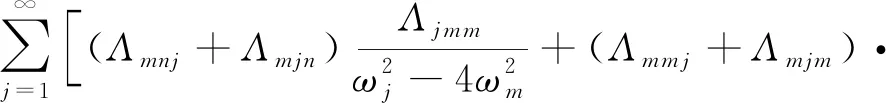
(Γmnmm+Γmmnm+Γmmmn)

(20)

(21)

3 數值算例與分析

數值算例中，懸索的物理參數為：L=200.0 m，A=7.069×10-2m2，E=200 GPa，ρ=7 800.0 kg/m3，g=9.81 m/s2，低階和高階模態的無量綱阻尼系數分別為0.005和0.006。

如圖2所示，基于特征值分析，可得懸索前十階模態頻率與Irvine參數λ2的關系。圖2中的(a)～(g)處，頻率之間多處呈現三倍關系，但由于模態正交性，在圖中(b)、(d)和(g)3處兩個正對稱模態之間可能發生3∶1內共振。其余情況雖然頻率之間呈現出公倍關系，但是系統不會發生模態間的耦合共振[19]。本文以第一階正對稱模態和第三階正對稱模態之間發生3∶1內共振為例，探究模態截斷對系統耦合共振的影響。已有研究表明：無論懸索或是斜拉索，即取前九階模態可反應其真實動力學行為。

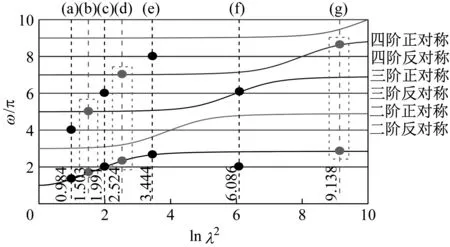
圖2 前10階模態頻率與Irvine參數關系

對于模態耦合共振，確定線性和非線性系數后，基于直角形式的平均方程式(16)～式(19)，給定合適的初始條件，利用Newton-Raphson法求得不動點，動態解(極限環)則利用打靶法求得。不動點的穩定性通過判斷其Jacobian矩陣的特征值來確定。有且僅有所有特征值的實數部分為負時，解為穩定，否則不穩定。在霍普夫分岔附近，不動點的穩定性會發生變化，此時基于Floquet理論來判斷極限環的穩定性。通過給定的初始條件，求得系統遠離共振區域的解，之后采用擬弧長延拓法得到其余區域的共振響應曲線。

因此基于兩階和九階模態截斷后的動力學方程，對比其激勵響應幅值曲線、幅頻響應曲線、時程曲線、相位圖、頻率譜、龐加萊截面和李雅普諾夫指數等，分析模態截斷對耦合共振的影響。

首先，假設外激勵直接作用在低階模態，兩調諧參數σ1和σ2分別選取為-0.2和0。圖3對比了截取系統前九階模態和僅考慮直接激勵和內共振兩個模態時的激勵響應幅值曲線。圖3中實線表示穩定解，虛線表示不穩定解，激勵直接作用在低階，因此a1為直接響應幅值，a5為由于能量傳遞引起的內共振響應幅值，SN和HB分別為鞍結點和霍普夫分岔，下標為分岔數，N為截取的模態數量。

對比圖3(a)和圖3(b)，直接激勵幅值f1從0逐漸增大，a1不斷增大，a5基本保持不變，直到第一個鞍結點分岔SN1。此處系統發生跳躍現象，幅值a1和a5將迅速增大。之后隨著f1繼續增加，a1依然不斷增大，a5則有可能增大或者減小，與跳躍點條件相關。兩者明顯的不同點在于：當采用兩模態截斷時，見圖3(b)，隨著激勵幅值f1增加，系統會額外出現兩個霍普夫分岔(HB1和HB2)，此局部區域內，系統將展現出更為復雜的非線性動力學行為。而截取前九階模態，動力系統并未展現霍普夫分岔。

當激勵幅值f1從0.006不斷減小到0時，除有無霍普夫分岔點這一明顯區別外，系統的第三個鞍結點分岔SN3也有差異。當采用九階模態截斷時，SN3將出現在更大的激勵幅值處，從而導致系統跳躍現象提前出現。由此可見，除局部共振區域外，模態截取階數對系統的共振響應幅值大小也有定量影響。而分岔與模態截斷的階數關系更為密切，僅考慮兩階模態，會使得該動力系統額外出現兩個霍普夫分岔，使得局部動態周期解變得更為復雜。

此外為驗證理論分析結果的正確性和可靠性，采用四階龍格庫塔法直接對截取兩個模態下的微分方程進行直接數值積分。得到的結果見圖3(b)，除響應幅值存在定量的差異外，兩者吻合較好。

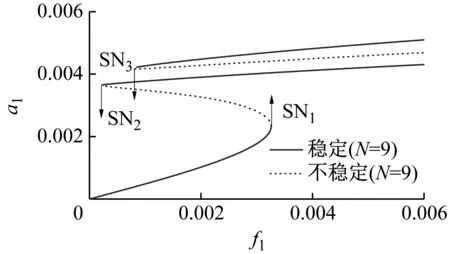
(a) 九階模態

接著，選取外激勵幅值f1為0.002 5，內調諧參數σ2=0，圖4給出了該非線性系統的幅頻響應曲線。截取前九階模態時，系統共振響應會出現3個鞍結點分岔(SN1, SN2和SN3)，直接導致3次跳躍現象發生。而兩模態截斷時，系統鞍結點分岔減少為兩個(SN1和SN2)，同時在小范圍內會額外出現兩個霍普夫分岔(HB1和HB2)。

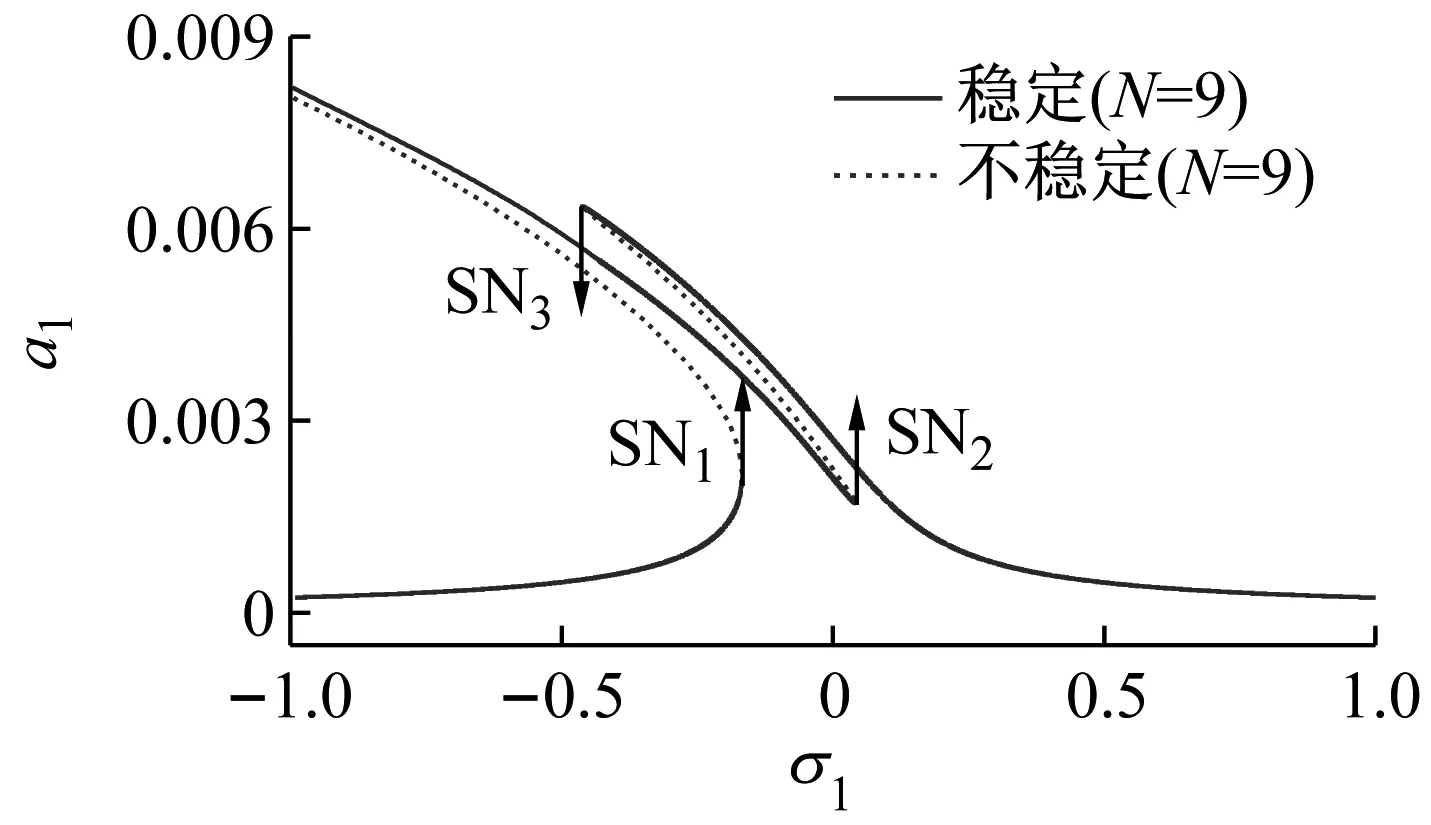
(a) 九階模態

對于直接激勵幅值a1而言，截取系統前九階模態時，由于新出現的鞍結點分岔SN3，當外調諧參數σ1由1.0不斷減小時，系統跳躍現象將提前發生，直接激勵響應振幅a1將突然減小。對于內共振響應幅值a5，隨著調諧參數從1.0不斷減小，兩模態離散時，a5隨之不斷增加，而九階模態截斷時，在SN3點附近會出現跳躍現象，導致a5突然增大。由此可見，在局部共振區域，不同階模態截斷會直接導致振幅出現較大區別。兩模態離散可能會遺漏分岔點(如：鞍結點分岔)以及出現額外的分岔(如：霍普夫分岔)。

同時，為了進一步展現兩類模態截斷方法導致計算結果區別，圖5給出了兩模態離散時系統的時程曲線、相位圖、頻率譜和龐加萊截面。此時外/內調諧參數和外激勵幅值分別選取為σ1=-0.15，σ2=0.3和f1=0.002 5。如圖5所示，兩模態截斷下的動力系統展現出明顯的混沌特性。

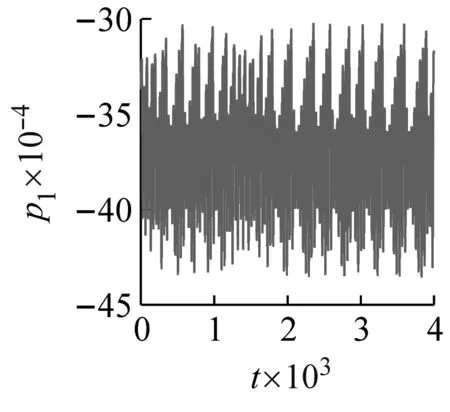
(a)

對于四維系統，當4個李雅普諾夫指數為(負；負；負；負)時，吸引子類型為不動點；指數為(零；負；負；負)為周期吸引子；指數為(零；零；負；負)為擬周期吸引子；指數為(正；零；負；負)為混沌吸引子。此處兩模態截斷時4個李雅普諾夫指數分別為：(0.012 933；-2.767 7×10-5； -0.010 464；-0.024 441)，即(正；零；負；負)，混沌吸引子。李雅普諾夫指數代表相軌道在某個維度的混亂程度，第二個指數與其他相比，相差3個量級。因此有限時間內，相比另外幾個維度，第二個指數所體現出的混亂程度在相位圖中可以忽略不計，其大小視為等于0。

選取相同參數，當系統截取前九階模態時，時程曲線如圖6所示，4個指數分別為：(-0.004 777 4；-0.005 205 9； -0.005 473 8；-0.006 542 8)，即(負；負；負；負)，該吸引子的類型為不動點。由此可見，不同階的模態截斷可能得到截然不同的吸引子類型。

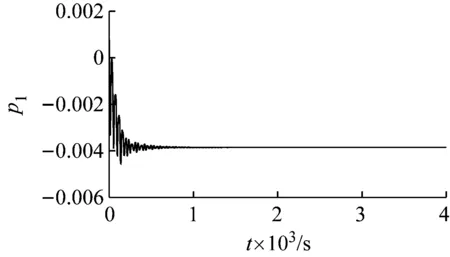
圖6 九階模態截斷時懸索的時程曲線

最后，上述分析均針對外激勵直接作用在低階模態，對于其作用在高階模態時，圖7給出了系統的幅頻響應曲線(f5=0.002 5和σ2=0)。與前一種工況不同的是，此時動力系統將明顯展現出兩類解：單模態解(a1=0和a5≠0)和內共振解(a1≠0和a5≠0)。

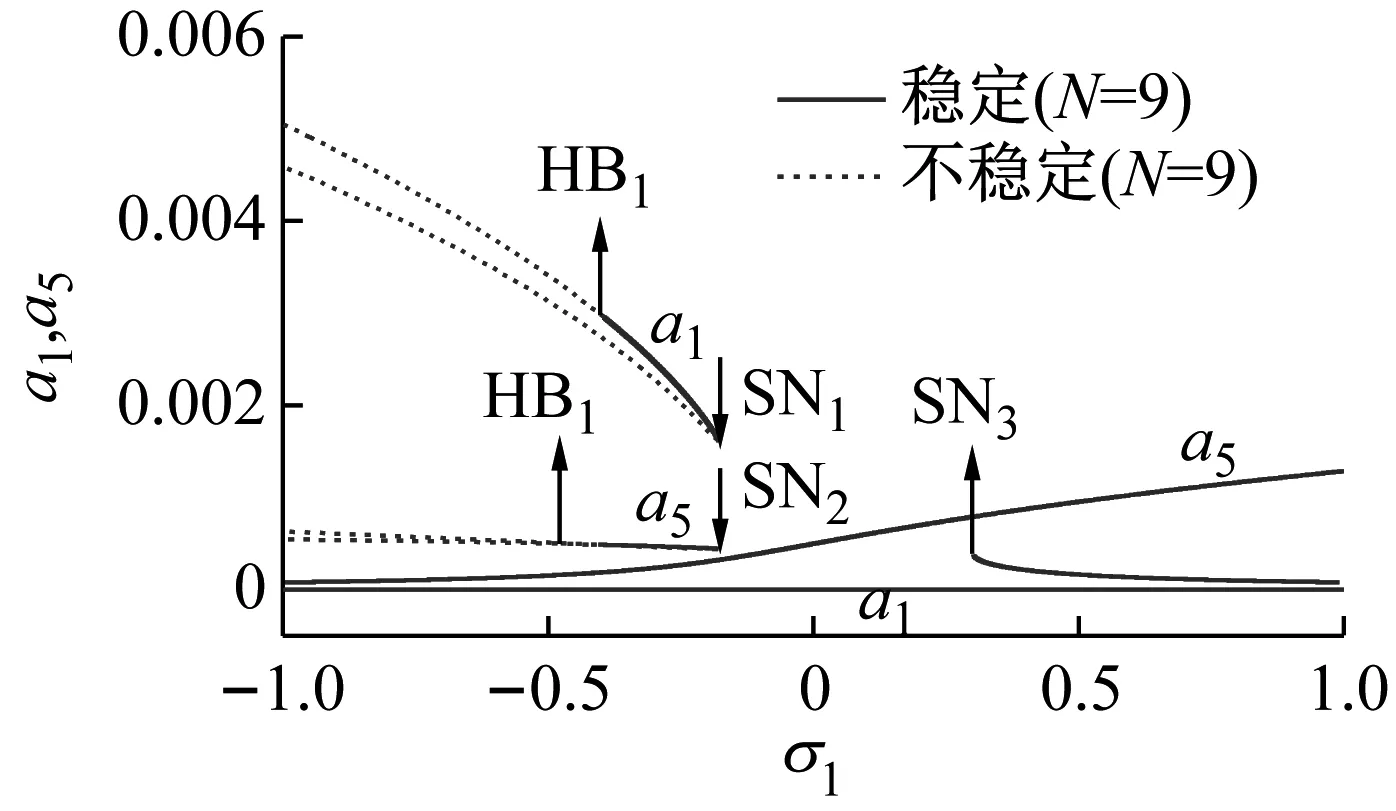
(a) 九階模態

對于單模態解，模態截斷對共振響應幅值的影響不明顯。而對于小范圍發生的內共振響應，除響應幅值和范圍稍微發生改變外，霍普夫分岔和鞍結點分岔數量和性質并未發生改變。因此當外激勵直接作用于高階模態時，模態截斷數對系統共振響應幅值和分岔影響要顯著降低。同時亦采用四階龍格庫塔法直接數值積分求解兩模態離散下的常微分方程組，積分結果如圖7(b)所示，可知吻合很好。

4 結 論

采用離散法結合攝動法求解非線性系統的微分方程，分析模態的耦合共振，計算結果的誤差來自兩方面：模態離散和攝動分析。結果表明：非直接激勵和非內共振模態會影響動力系統的內共振響應，根源在于平方非線性導致的共振項；對于外激勵直接作用在低階和高階模態的情況，不同階的模態截斷導致系統動力學特性的差異程度，前者要明顯高于后者；在局部耦合共振區域，模態截斷對系統共振響應幅值大小影響明顯；分岔與模態截斷的階數密切相關，僅考慮兩階模態時，分岔分析可能會遺漏鞍結點分岔或會新增霍普夫分岔；不同階的模態截斷有可能導致系統出現截然不同的吸引子類型，比如：混沌或不動點；倘若僅分析內共振的穩定解，除局部共振區域，兩階模態離散可以滿足分析需要；倘若要分析該系統分岔和周期運動，宜采用多階模態截斷。