基于BA-RVM算法的發動機故障診斷技術研究*

陳財森,胡海榮,程志煒,房璐璐

(1.陸軍裝甲兵學院演訓中心，北京 100072； 2.陸軍裝甲兵學院信息通信系，北京 100072；3.32167部隊，西藏 拉薩 850000)

1 引言

為了打贏信息化戰爭，裝備保障技術同樣也需要信息化。發動機是裝甲裝備的核心部件，直接關乎到裝甲裝備的作戰能力。傳統的故障診斷技術已經不適用于大規模裝甲裝備的故障診斷，在信息化條件下，結合人工智能技術對故障進行預測判斷，高效率高準確率地定位故障可以提高裝備保障的質量，才能快速恢復戰斗力。

1985年，美國的通用汽車公司就已經開始對汽車的發動機故障診斷進行研究[1]，此后，一些發達國家的汽車發動機故障診斷系統也得到迅速發展。我國的發動機故障診斷技術研究起步較晚，但到目前為止，我國的發動機故障診斷技術也已經相對成熟。文獻[2,3]利用神經網絡對發動機的故障進行預測，并能確定故障的原因。文獻[4]利用波形和數據流診斷汽車發動機的電控系統故障。故障診斷技術發展到現在，雖然結合了新的分析方法，如BP(Back Propagation)神經網絡、支持向量機SVM(Support Vector Machine)和貝葉斯分布等算法，但是預測的準確率仍然不高，且由于應用對象不同，其技術還無法直接應用在裝甲裝備發動機的故障診斷上。

2 發動機故障參數分析

發動機運行時，傳感器會采集發動機的各種參數，這些參數被稱為數據流，包括發動機的節氣門開度、轉速、氧傳感器等參數。本文采集如表1所示的9個典型的發動機參數進行分析。

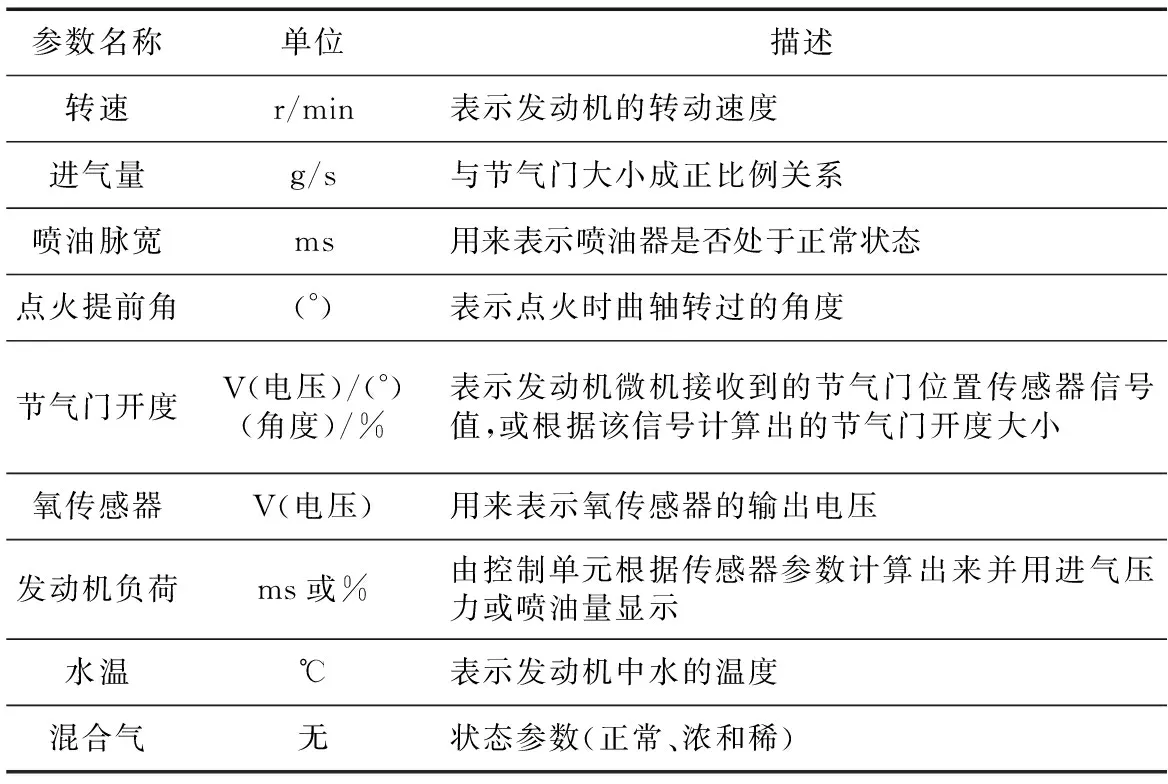
Table 1 Typical engine parameters表1 發動機典型參數

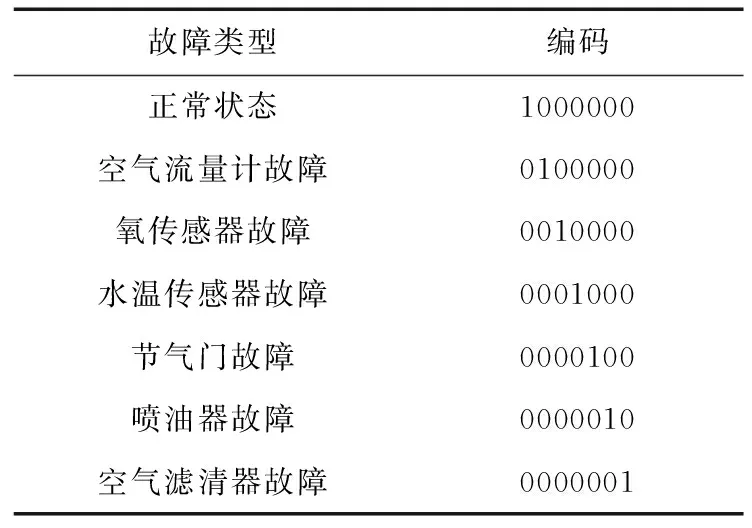
通過分析表1所示的9個參數，能夠確定6種故障，分別是空氣流量計故障、氧傳感器故障、水溫傳感器故障、節氣門故障、噴油器故障和空氣濾清器故障。不同的傳感器采集數據的單位不一致，導致這些數據無法直接使用。因此，在使用數據前，必須對其進行預處理，以免某一個參數的巨大變化導致模型預測失真。通過采集大量的發動機參數信息與故障信息，訓練出一個合理的預測模型，然后直接輸入傳感器參數的數據快速準確地得到故障類型。

3 基于BA-RVM算法的發動機故障診斷模型

3.1 蝙蝠算法

劍橋大學Yang教授[5]在2010年提出一種模擬蝙蝠捕獲獵物時使用超聲波的啟發式搜索算法，被稱為蝙蝠算法BA(Bat Algorithm)。蝙蝠在利用超聲波判斷獵物的過程中，如果靠近獵物，其發出的脈沖數量將會增加，并且響度會減小，直到蝙蝠捕獲獵物。蝙蝠尋找獵物的過程可轉換為尋找最優解的問題。蝙蝠算法將每一個蝙蝠作為搜索空間的一個解，通過蝙蝠隨機飛行產生的適應值來尋找下一次迭代的最優值，當蝙蝠隨機飛行產生的適應值優于飛行之前的適應值，則更改蝙蝠的位置，否則保持蝙蝠的位置不變，將在下一次迭代中繼續隨機飛行，直到得到比當前蝙蝠的適應值更優的位置。所以，蝙蝠總是朝著最優解前進，最終收斂于問題的最優解。與遺傳算法和粒子群優化算法相比，蝙蝠算法的效率和準確率都有明顯的提高[6]。在算法循環迭代過程中，通過改變蝙蝠的速度、響度和頻率來尋找局部最優解，直到局部最優解收斂或者完成指定迭代次數。

算法1蝙蝠算法BA

輸入：所有蝙蝠的位置xi，所有蝙蝠的速度vi。

輸出：最優蝙蝠的位置xbest。

步驟1初始化蝙蝠位置xi和蝙蝠的初始速度vi，其中i∈[1,n]，n為種群的數量。

步驟2初始化種群飛行時脈沖響度Ai、脈沖發射率ri及脈沖頻率fi，并確定頻率搜索范圍[fmin,fmax]，根據適應值函數計算初始化蝙蝠種群的適應值，并記錄最優適應值fitnessbest和最優位置xbest。

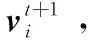
fi=fmin+(fmax-fmin)β

(1)

(2)

(3)

其中，β∈[0,1]是服從均勻分布的隨機數，xbest為全局最優位置。

步驟4生成一個隨機數rand1，如果rand1大于脈沖發射率ri，對最優蝙蝠位置xbest進行擾動，產生新值進行替換，以降低算法陷入局部最優的概率。擾動公式如式(4)所示：

(4)

其中，ε是[0,1]的隨機數，A(t)是當前時刻t時所有蝙蝠脈沖響度的平均值。

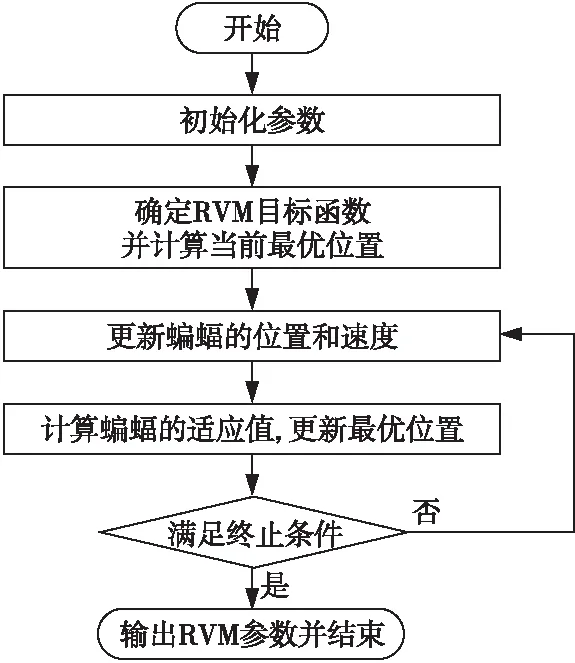
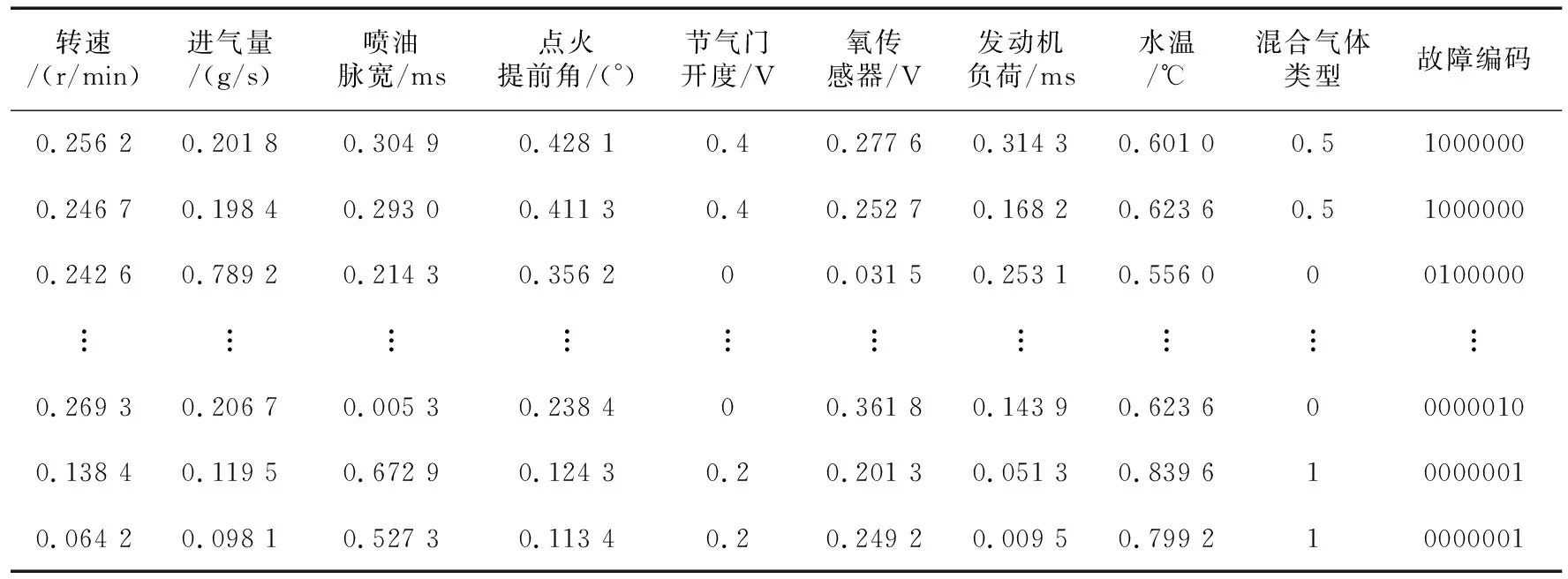
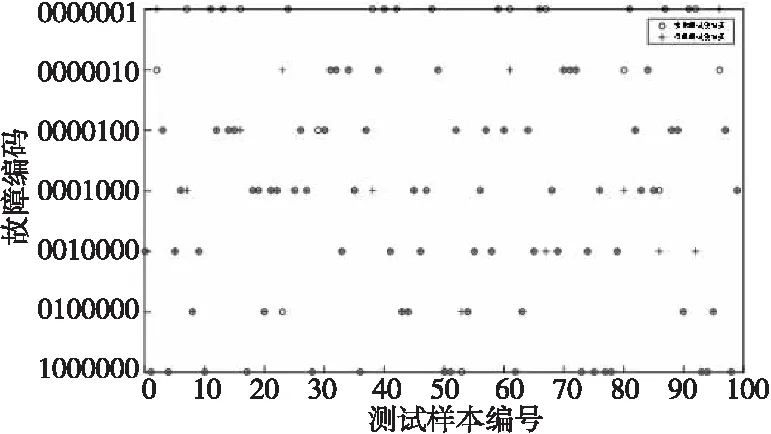
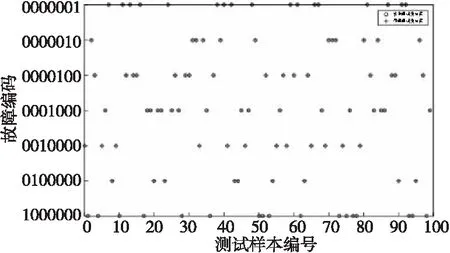
步驟5再次生成一個隨機數rand2，如果rand2小于脈沖響度Ai且更新后的位置適應值fitnessi

(5)

(6)

其中，α∈(0,1),γ>0。

步驟6重復執行步驟3～步驟5，直至滿足設定的最優解xi的條件或者達到最大迭代次數。

步驟7輸出全局最優適應值和最優解。

3.2 相關向量機算法

ti=y(x;ω)=

(7)

其中，ωi表示權重，δ是服從N(0,σ)分布的噪聲，x表示位置矩陣，ω表示權重向量，K(x,xi)是核函數，Φ(x)由N×(N+1)階的核函數構成，如式(8)所示：

(8)

本文假設ti服從獨立分布，樣本的概率表達式如式(9)所示：

p(t|ω,σ2)=

(9)

其中，t表示ti的矩陣。為防止ω和σ2過渡擬合，一般使用高斯先驗概率分布對參數進行約束，如式(10)所示：

(10)

其中α為N+1維超參數向量。

后驗分布基于Bayes公式，如式(11)和式(12)所示：

p(ω|t,α,σ2)=(2π)-(N+1)/2|Σ|-1/2×

(11)

μ=σ-2ΣΦ(x)2t

Σ=(σ-2Φ(x)TΦ(x)+A)-1

(12)

A=diag(α0,α2,…,αN)

這里統一使用超參數表示，RVM的概率表達式p(t|α,σ2)的定義如式(13)所示：

(2π)-(N+1)/2|σ2Ι+Φ(x)A-1Φ(x)T|-1/2×

(13)

最后求解p(t|α,σ2)的最大值,如式(14)所示：

p(t|α,σ2)∝p(t|α,σ2)p(α)p(σ2)

(14)

從而得到求解最大值的公式,如式(15)所示：

(15)

設新的輸入和輸出為(x*,t*)，通過以上分析，輸出t*的均值和方差如式(16)和式(17)所示：

y*=μTΦ(x*)

(16)

(17)

核函數能夠將復雜難分的數據映射到高維空間，使數據更容易區分，RVM常用的核函數有：

(1)高斯核函數：對樣本數據的維度和大小沒有限制，局部尋優能力較強，應用較為廣泛，如式(18)所示：

(18)

其中，p和q是空間中任意2點的向量表示。

(2)多項式核函數：與高斯核函數相比，多項式核函數的全局尋優能力更強，但是參數n調節過大時，容易產生過擬合現象，且需要消耗大量的計算資源，如式(19)所示：

K(p,q)=(apTq+c)d

(19)

其中，a表示調節參數，c用來設置核函數中的coef,d表示最高次項次數。

(3)拉普拉斯核函數：是高斯核函數的一個變種，具有降低核參數敏感性的特征，如式(20)所示：

(20)

在RVM訓練的過程中，通過迭代得到最終的模型權重值，再根據式(7)進行分類。文獻[7]在求RVM參數時，通常把核矩陣剪枝閾值設置為107，終止迭代閾值設置為10-3，以便在有限迭代中盡早獲取合適的參數。

3.3 BA-RVM算法

RVM算法的核心是獲取一個合適的參數，因此核函數的選擇對RVM算法分類結果的影響特別大，將直接影響RVM的判斷準確率。本文使用BA作為核函數來尋找RVM的最優參數。

算法2BA-RVM算法

輸入：BA和RVM算法參數。

輸出：xbest。

步驟1初始化BA和RVM算法的參數，并按照Tipping[7]的經驗值設置核矩陣剪枝閾值。

步驟2確定RVM的目標函數，把BA中的蝙蝠作為當前RVM核參數寬度計算目標的值，得到最優位置xbest。

步驟3對蝙蝠的速度vi和位置xi進行隨機更新。

步驟4計算蝙蝠的目標函數值，如果優于目標函數值xbest，則更新局部最優位置xbest。

步驟5重復步驟3和步驟4，直到迭代次數達到最大或滿足RVM的閾值條件。

基于BA算法自適應核參數RVM的流程如圖1所示。

Figure 1 Flow chart of adaptive kernel parameter RVM based on BA 圖1 基于BA自適應核參數RVM的流程圖

3.4 數據特征歸一化方法

發動機傳感器采集的每個參數的量綱和單位不一樣，如果不對數據進行預處理，將會導致數值大的參數對結果影響過大，所以在數據分析前，需要對樣本數據進行歸一化處理，以保證實例各參數值處于同一個數量級，消除不同量綱之間的差異。通常歸一化有線性歸一化(Min-Max Scaling)和Z-score標準化(Z-score Standardization)2種方法：

(1)線性歸一化，如式(21)所示：

(21)

其中，Xi表示樣本實例數據，Xmin表示樣本實例數據的最小值，Xmax表示樣本實例數據的最大值，X*表示歸一化處理后的數據。這種歸一化也叫做離差標準化，通過對樣本實例數據進行線性變化，使處理后的數據值在[0,1]。這種方法適合樣本實例數據比較穩定，沒有異常極端值的情況。

(2)Z-score標準化，如式(22)所示：

(22)

其中，Xi表示樣本實例數據，μ表示樣本實例數據的均值，σ表示樣本數據的標準差，X*表示歸一化處理后的數據。經過Z-score標準化后的數據符合高斯分布，這種方法適合處理樣本實例數據存在異常值和較多噪聲的情況。通過Z-score標準化，能夠避免異常值和極端值給結果帶來的影響。

4 實驗與結果分析

本文實驗的操作系統環境為Ubuntu 18.04，CPU為Intel Core i5-7500，顯卡為NVIDIA GTX1050i，內存為16 GB。在發動機故障診斷中，選擇高斯核函數和線性歸一化函數的預測效果最佳[8]。本文的6種故障類型屬于離散數據，為了讓分類器更好地處理數據，實驗對故障類型和正常狀態進行one-hot編碼，編碼規則如表2所示。

Table 2 One-hot coding of fault type 表2 故障類型one-hot編碼

本文采集12/200ZL型水冷廢氣渦輪增壓柴油機的樣本數據500條，其中400條用于訓練，100條用于測試(隨機從總樣本中抽取)。通過使用線性歸一化函數，將數據進行歸一化處理，部分樣本數據如表3所示。

Table 3 Normalized engine data stream表3 歸一化后的發動機數據流

為了讓實驗結果更具代表性，本文同時使用BP神經網絡和SVM算法對同一份數據進行訓練預測并將測試結果與BA-RVM的進行比較。首先使用BP神經網絡對數據進行訓練預測，將BP神經網絡的隱藏節點設置為10，測試結果如圖2所示。圖2中的縱坐標表示故障編碼，橫坐標表示測試樣本的編號。從圖2可以看出，BP預測的錯誤率為12%，結果較為理想。

Figure 2 Testing results of BP neural network圖2 BP神經網絡的測試結果

BA-RVM算法的測試結果如圖3所示。可以看到，錯誤率只有3%,與BP算法相比，錯誤率降低了66.67%;與SVM算法相比，錯誤率降低了62.5%。由于RVM中有大量的矩陣運算，在訓練過程中，消耗的時間較長，約為SVM算法的6倍，但是在預測判斷時，所消耗的時間少于SVM的，能夠快速準確地給出結果。綜合分析可知，基于BA-RVM算法的發動機故障預測要優于基于BP算法和SVM算法的，并能夠快速定位故障類型。

Figure 3 Testing results of BA-RVM algorithm圖3 BA-RVM算法的測試結果

5 結束語

本文針對傳統檢測技術在大量故障裝備中難以準確快速診斷發動機故障，且診斷工作量大、效率低等問題，提出一種基于BA-RVM算法的發動機故障診斷模型。通過分析蝙蝠算法BA獲得最優解的特點和相關向量機算法原理，結合裝甲裝備發動機的狀態參數特點，在故障診斷分析模型訓練時，采用蝙蝠算法對相關向量機算法RVM的核參數寬度進行調節優化，使用BA作為核函數來尋找RVM的最優參數，從而得到RVM最優參數的預測模型。實驗結果表明，本文所提的基于BA-RVM算法的模型與基于BP算法的模型相比，錯誤率降低了66.67%;與基于SVM算法的模型相比，錯誤率降低了62.5%。基于BA-RVM算法的發動機故障診斷模型不僅能夠快速地給出預測結果，而且預測準確率還較高。