計及系統參數和負荷電流影響的故障測距方法

張洪喜，徐海洋，卜立之，徐曉春，黃濤

（南京南瑞繼保電氣有限公司，江蘇 南京 211102）

關鍵字：故障測距；過渡電阻；系統阻抗；分配系數；鄰線互感

0 引言

高壓輸電線路是電力系統的命脈，擔負著傳輸電能的重任，同時，又是系統中發生故障最多的地方，并且極難查找。在線路故障后迅速準確地找到故障點，能夠及時修復線路和保證可靠供電，對電力系統的安全穩定和經濟運行都有十分重要的作用［1-3］。輸電線路布線很長，尋找故障位置有很大困難，人工巡線尋找故障位置要花費很多時間，因此需要故障測距裝置的協助。當故障發生時，故障測距裝置能根據不同的故障特征迅速準確地測定故障點，這不僅大大減輕了人工巡線任務，還能查出運維人員難以發現的故障，能夠有效提升電力生產部門的社會效益和經濟效益。目前故障測距有多種方法，按測距原理可以分為故障分析法和行波法；根據測距所需要的信息來源可分為單端測距法和雙端測距法［2-6］。

故障分析法是在輸電線路發生故障時，根據系統有關參數和測距點的電壓、電流列出測距方程（一般為電壓方程），然后對其進行分析計算，求出故障點到測距點之間距離的一種通用方法。該方法不僅適用于單端量測距，而且適用于雙端量測距，二者的區別僅在于前者利用輸電線路一端的電壓、電流信息，后者利用了線路兩端的電壓、電流信息。故障分析法又可分為阻抗法、電壓法和解方程法。阻抗法利用故障時在線路一端測到的電壓、電流計算出故障回路的阻抗，進而求出故障距離；電壓法則在故障條件下根據電壓沿線路分布的特征求出故障點的位置；解方程法根據輸電線路參數和系統模型，利用測距點的電壓、電流，用解方程的方法，直接求出故障點的距離。解方程法包括解復數方程和解微分方程，前者在頻域內求解，后者在時域內求解。解方程法既可用于單端量測距，也可以用于雙端量測距。雙端測距需要獲取對側電氣量，同時需要兩側數據嚴格同步，對使用條件提出了較高的要求［5-7］。

行波法是根據行波理論實現的測距方法，行波法也可分為單端量法和雙端量法，前者利用線路一端檢測到的暫態行波量實現，后者利用線路兩端的暫態行波量實現故障測距。行波測距法需要特殊的硬件資源，需要較高的采樣率，增加了使用和維護成本［6-8］。

單端測距僅依賴本側電氣量，不需要額外的硬件資源，因此，目前單端測距得到了普遍應用［8-10］。由于單端測距僅依靠單端電氣量，因此易受過渡電阻和相鄰線零序互感的影響。為此常規單端測距算法考慮了過渡電阻和零序互感的影響。為了簡化計算，在工程實現時，常規單端測距對系統阻抗、故障電流等做了近似假設。這些假設會影響測距精度，尤其是經過渡電阻故障時，影響程度更大。

從一起現場故障測距異常入手，分析實際線路經過渡電阻故障時，產生測距誤差的原因，提出一種測距新方法。新方法考慮了系統參數，負荷電流和零序互感的影響因素，有效提高故障測距精度。

1 故障測距誤差分析

2021-10-16T12：57：05，南美洲某國230 kV 線路發生一起A相經過渡電阻故障，線路全長為18.7 km。保護裝置采用單端測距原理，測距結果為37.4 km。根據故障巡線結果，實際故障位置為15.8 km，二者相差較大。為此須對現有單端測距算法進行分析，找出影響測距的因素。

在電力系統中，任何復雜系統均可等值為簡單兩機系統。在線路各種故障類型中，單相接地故障占比最大，且易受過渡電阻的影響［11-13］。以兩機等值系統為研究對象，以單相經過渡電阻故障為例進行分析，如圖1所示。

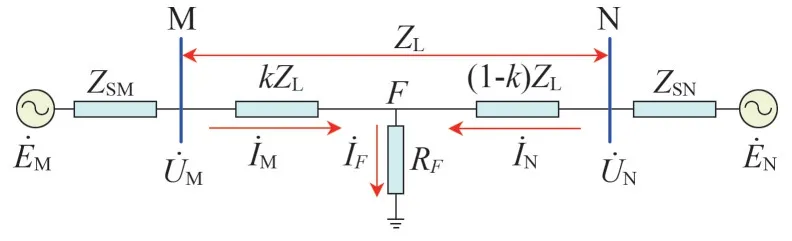
圖1 單相經過渡電阻故障

當線路發生經過渡電阻故障時，根據基爾霍夫電壓定律，對M側有式（1）成立［5］。

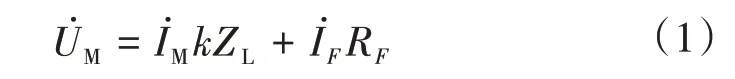
根據式（1）可得測量阻抗方程，即

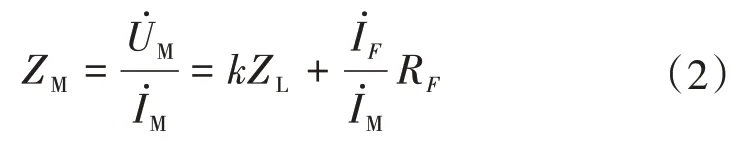
式（2）中等式右邊包含過渡電阻引起的附加測量阻抗，將會嚴重影響測距精度［11］。且式（2）中有兩個未知數RF和，無法直接求解。為了便于計算，現有單端測距方法做了一些近似假設［13］。

其中，零序分配系數為

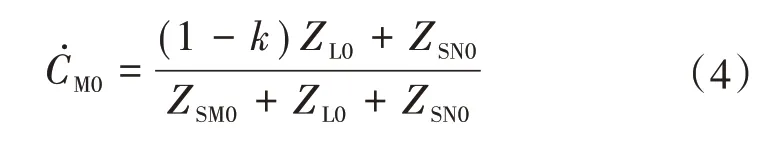
式中：ZSM0、ZSN0分別為M 側、N側等值系統零序阻抗；ZL0為線路MN零序阻抗。

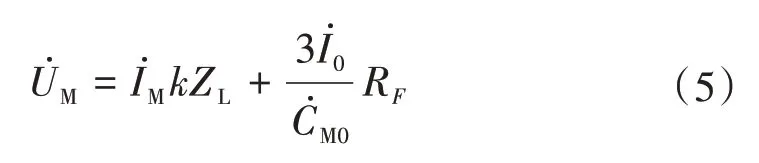
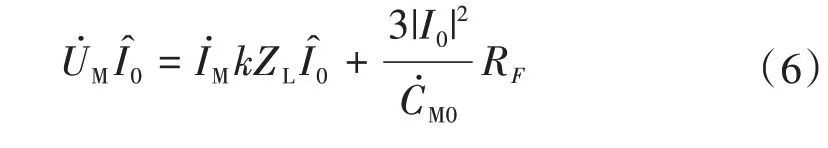
實際系統中，線路兩側背后系統阻抗角近似等于線路阻抗角，因此零序分配系數假設為一實數。將式（6）兩邊同時取虛部即可消掉過渡電阻分量，進而求得故障位置系數，并最終求出實際故障位置。

2 故障測距改進算法

通過以上分析，對系統參數等的近似假設是目前單端測距產生誤差的主要原因。下面不做任何假設，通過嚴格的物理模型和數學推導，提出改進測距方法。

根據分配系數的定義，M 側分配系數CM計算公式為

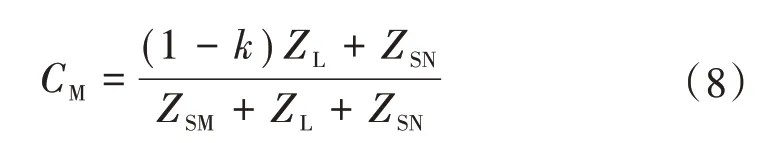
對于單相接地故障，根據故障點邊界條件，有關系成立如式（9）所示［13-14］。

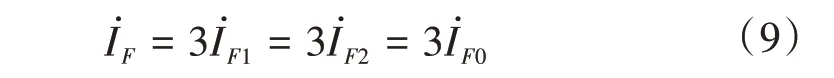
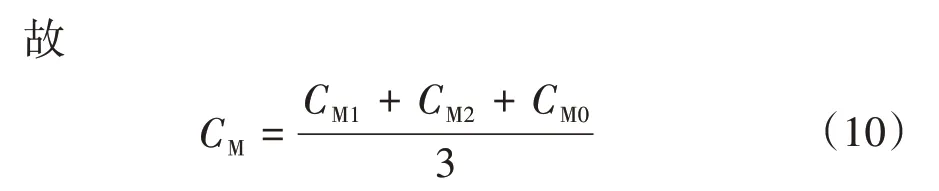
式中：CM1、CM2、CM0分別為M側正序、負序和零序分配系數。又因為正序和負序阻抗相等，所以有式（11）—式（12）成立。

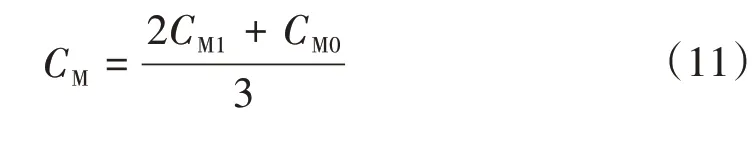
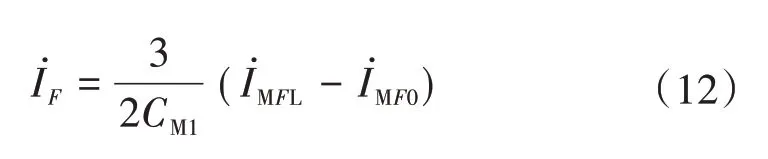
根據疊加原理，故障分量電流可以通過故障前后電流變化量獲得［15-17］。則M 側故障電流分量可通過M 側故障前后變化量獲取。因此，故障點故障電流又可表示為

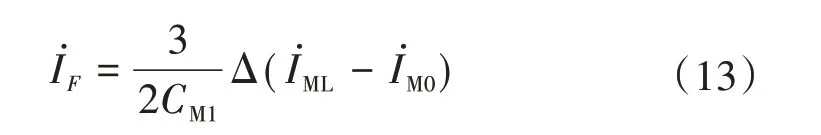
對于接地故障，式（1）可以表示為

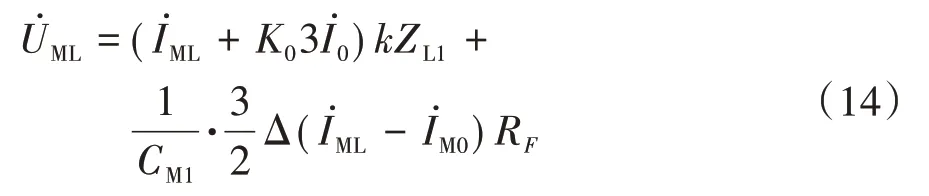
同理，對于相間故障，故障點電流為

相間故障時，式（1）可以表示為

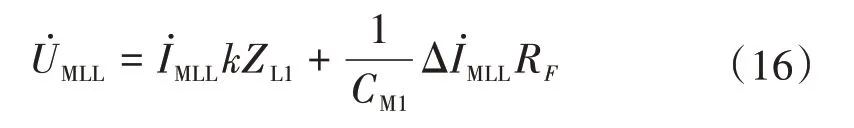
M側正序分配系數計算方法為

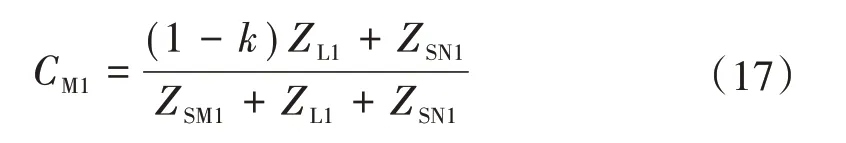
根據上述分析，將式（14）和式（16）合并統一為普適公式（18）。

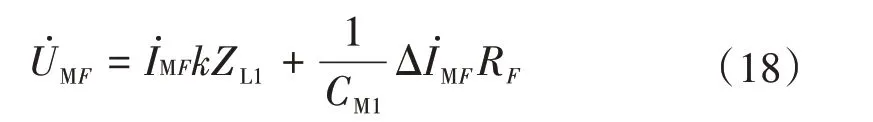
將式（18）進行化簡，得到關于k和RF的方程，如式（19）所示。

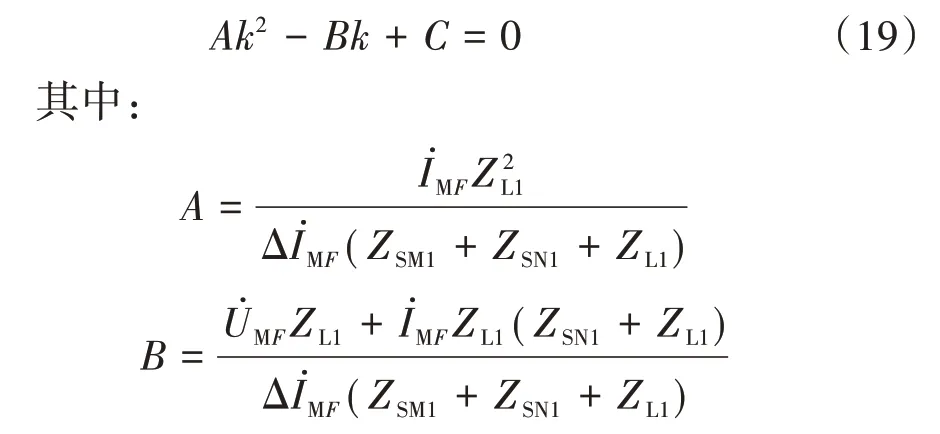
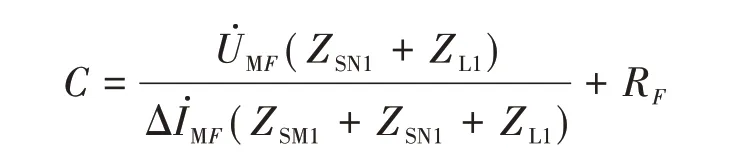
式（15）中有未知數RF，由于其為實數，因此將等式兩邊取虛部，消去RF后得到關于k的二元一次方程。

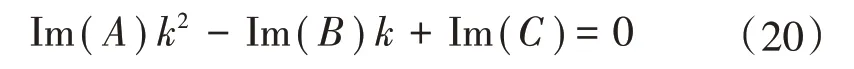
根據求根公式，二元一次方程的根為

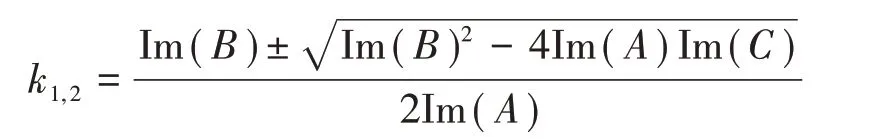
當線路發生區內故障時，有k∈(0,1)，且本側和對側測距結果之和應為1，根據這些原則剔除偽根。通過一元二次方程直接求根能避免迭代法可能不收斂的問題。

通過以上分析和推導過程，新測距方法對克服了系統參數和負荷電流的影響。

利用新方法對現場故障重新測距，實測結果為15.91 km。該結果與實際故障位置（15.8 km）相比，誤差約為0.7%，有效提高了測距精度。

3 零序互感的影響

對于雙回線，在發生接地故障時，兩回線之間存在零序互感，需要考慮零序互感電流對測距的影響［17-19］。則有

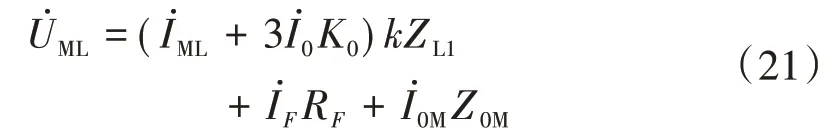
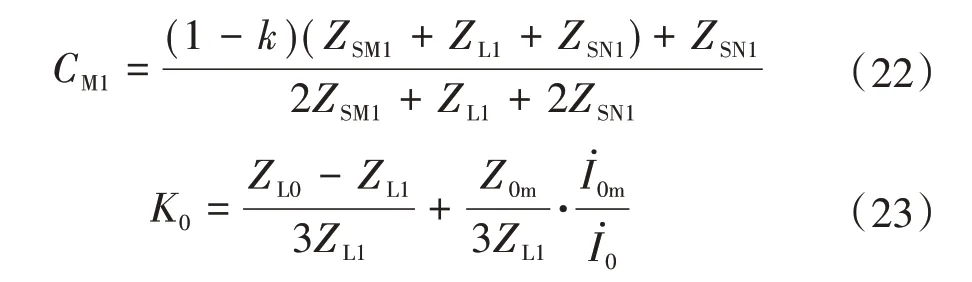
因此，對于雙回線，將正序分配系數和零序補償系數替換為式（22）和式（23）即可。

4 系統阻抗的計算

獲取精確的系統阻抗是改進測距算法的前提。在上述分析中均用到系統正序阻抗，其受運行方式影響。為提高測距精度，應實時計算故障時系統兩側的阻抗。根據疊加原理可以將故障網絡分解為故障前負荷網絡和故障附加網絡［11-13］。故障附加網絡如圖2所示。

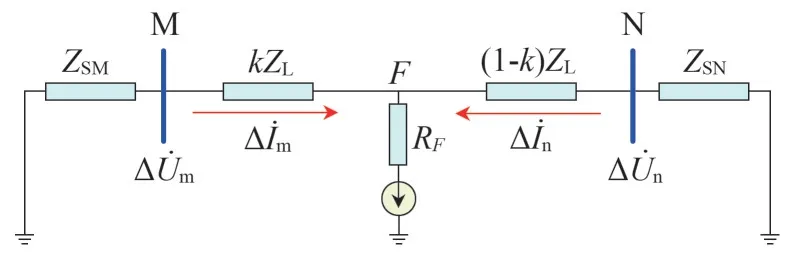
圖2 故障附加網絡

根據圖2，M側系統阻抗計算公式為

故障附加網絡中的電流和電壓通過故障前后電流和電壓變化量來獲取。進而根據對稱分量法獲取兩側保護裝置的正序系統阻抗ZSM1和ZSN1。對側系統阻抗可通過公用網絡傳到本側。在不增加成本的同時，避免對側系統阻抗估算帶來的誤差。

5 仿真分析

為考察提出的測距算法在實際系統中的效果，采用東南亞某國實際電網模型進行仿真分析［19-22］。

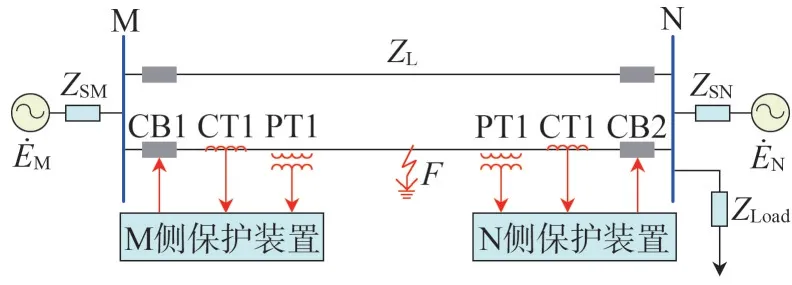
圖3 仿真系統模型

該系統電壓等級為500 kV，系統額定頻率為50 Hz，線路長度為200 km，負荷ZLoad為（1 141+j181）MVA。其他參數如表1所示。

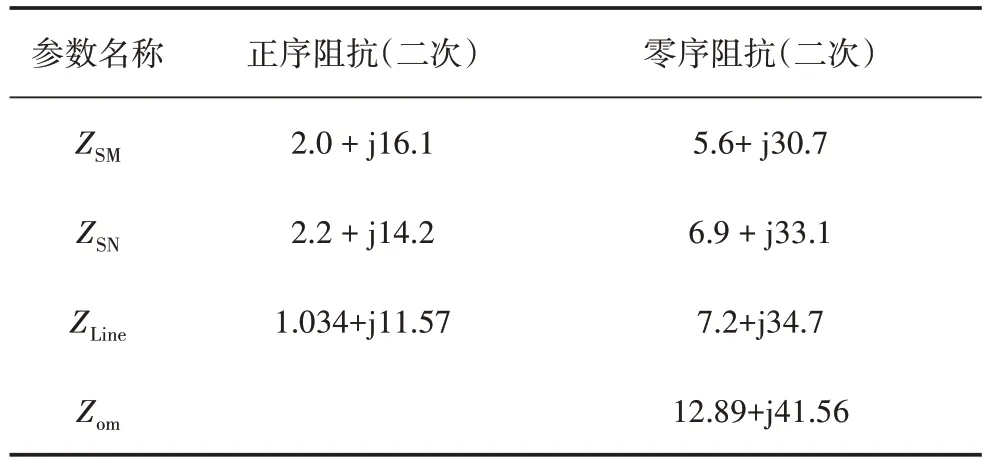
表1 仿真模型參數 單位：Ω

按照上述參數搭建RTDS 模型，模擬F點故障（其中F點位置可調，故障類型和過渡電阻可設）。將仿真數據讀入到MATLAB中進行仿真分析。

5.1 正序系統阻抗分析

為驗證正序系統阻抗實時計算的準確性，斷開負荷，退出相鄰線路，模擬本線路區內50%處單相接地故障。根據本文提供的方法繪制正序系統阻抗曲線，如圖4所示。

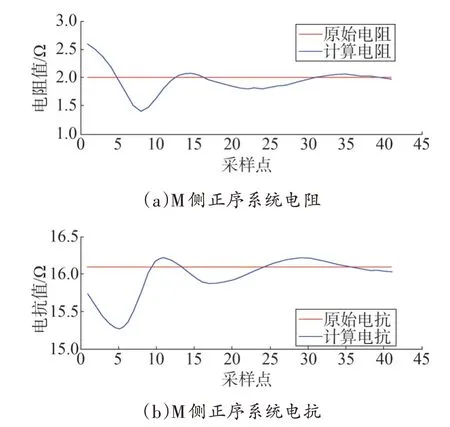
圖4 M側系統正序阻抗曲線

從圖4 可以看出，在線路發生故障后一個周波內計算阻抗與原始阻抗參數基本達到一致，驗證了方法的正確性。

5.2 高阻故障測距分析

為驗證高阻故障時測距精度，退出相鄰線路，分別模擬本線路50%處單相和相間經過渡電阻故障（單相和相間故障電阻均為50 Ω）。根據本文提供的方法進行測距計算，如圖5所示。

從圖5 可以看出，本線路50%處經過渡電阻故障時，故障一個周波后測距達到穩定狀態。故障后一個周波時，接地和相間測距結果分別為100.8 km和100.5 km，誤差分別為0.4% 和0.25%，均小于0.5%，能滿足實際工程要求。

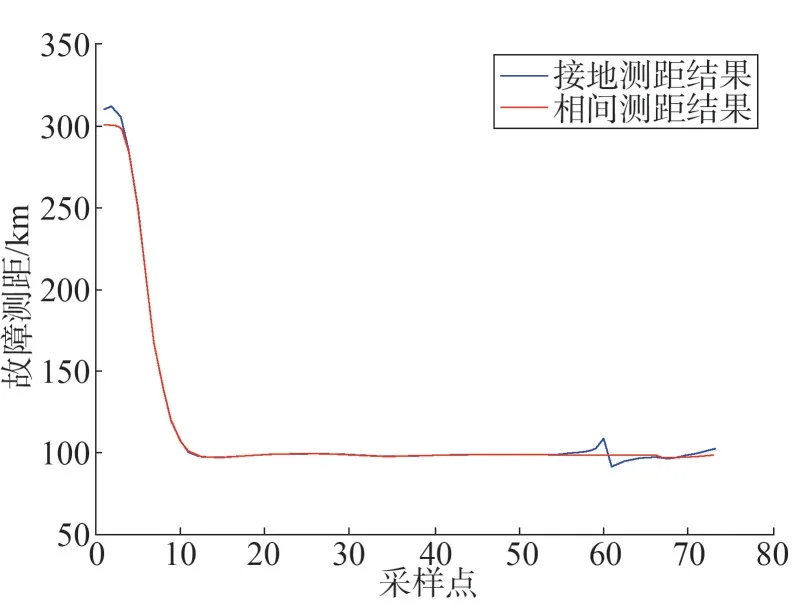
圖5 線路50%處高阻故障測距曲線

5.3 互感對測距的影響分析

為驗證鄰線互感對測距精度的影響，投入相鄰線路，模擬本線路50%處單相接地故障。根據本文提供的方法進行測距計算，仿真結果如圖6所示。

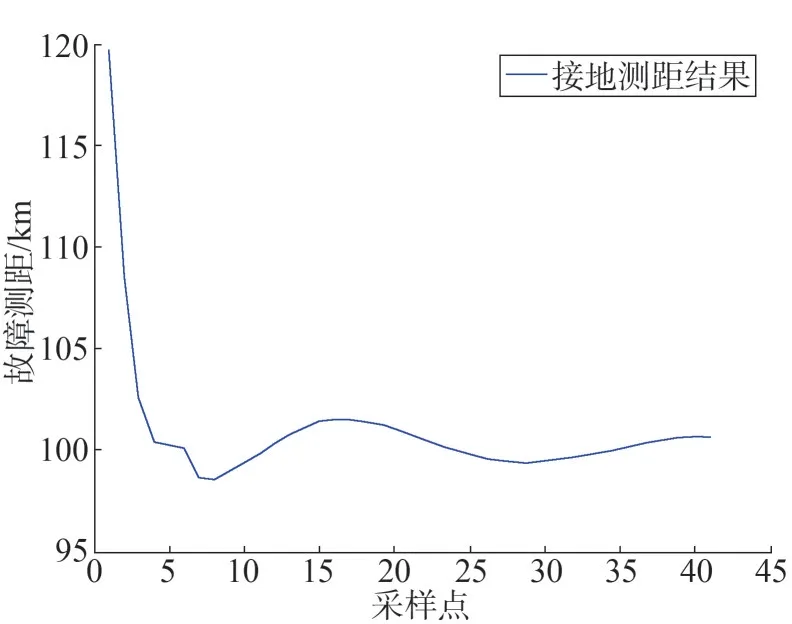
圖6 雙回線50%處接地故障測距曲線

從圖6可以看出，雙回線路本線50%處接地故障時，故障一個周波后測距結果趨于穩定。故障一周波時測距結果為100.9 km，誤差為0.45%，小于0.5%。證明本文提出的算法能有效避免鄰線互感的影響。

選取部分仿真測試數據，如表2所示。

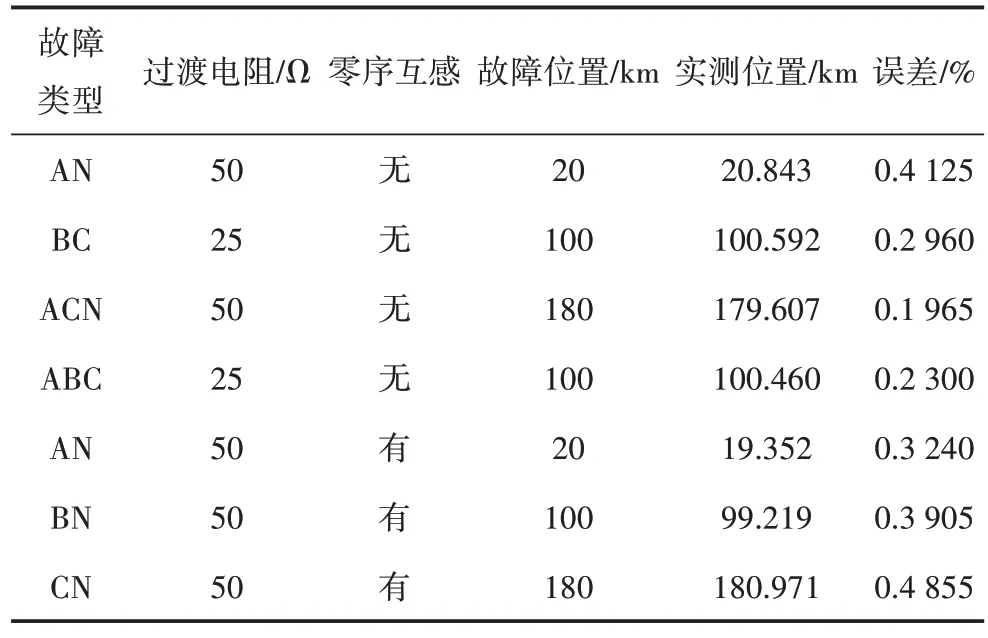
表2 故障測距結果

通過表2 可以看出，本文提出的基于單端電氣量改進故障測距算法能有效克服過渡電阻和零序互感的影響，在不同故障類型和不同故障位置情況下，測距誤差均小于0.5%，極大提高了故障測距精度。

5.4 改進前后測距精度比較

為了驗證本文提出的改進測距算法的有效性，分別模擬線路不同位置不同故障類型經過渡電阻故障，考察改進前后測距算法的測距結果，如表3所示。

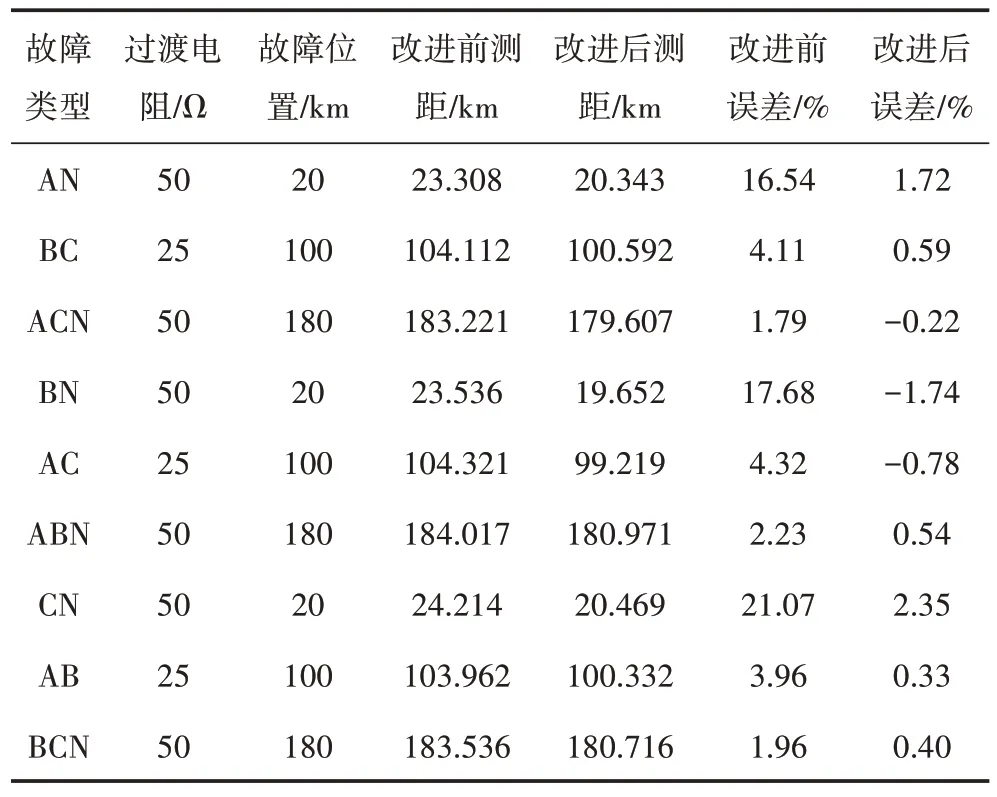
表3 改進前后測距結果比較

通過表3 可知，在相同的故障位置、相同故障類型和相同過渡電阻故障情況下，改進后測距算法精度明顯優于改進前測距算法，且基本能滿足工程2%的誤差要求。

6 結語

從一起現場故障測距異常入手，分析實際線路經過渡電阻故障時，產生測距誤差的原因，提出一種測距新方法。首先利用故障前后電流變化量計算故障電流分量；再根據兩側系統阻抗和線路阻抗計算故障電流分配系數，進而推出故障點故障電流；然后利用保護安裝處電壓電流測量得到故障測距方程并求出方程的根。提出了去除偽根的方法，考慮了雙回線鄰線互感零序電流的影響，同時提出了實時計算系統阻抗，以及獲取對側系統阻抗的方法。本文提出的測距方法考慮了系統參數，負荷電流等影響因素。能有效避免過渡電阻和鄰線互感的影響，能適應不同的運行方式。最后通過仿真分析，驗證了方法的正確性。