永磁同步電機并聯法模型預測轉矩控制*

李耀華， 張鑫泉， 董國慶， 鄧益志， 李茂盟， 童瑞齊， 丁 紅， Rajibul Islam

(長安大學 汽車學院，陜西 西安 710064)

0 引 言

永磁同步電機(PMSM)有限狀態集模型預測轉矩控制(FCS-MPTC)將電機與逆變器視為一體，根據兩者的離散模型和電機當前控制變量的狀態，遍歷逆變器所有電壓矢量，對未來時刻的電機控制變量進行預測，通過體現控制目標的成本函數評估電壓矢量，從而選擇最優電壓矢量作用于電機。由于MPTC概念清晰、控制直觀，具有較強的柔性，可實現多變量協同控制和非線性約束，其近年來受到廣泛關注[1-5]。MPTC的控制變量為不同量綱的磁鏈和轉矩，需要設置和調整權重系數來平衡磁鏈控制和轉矩控制。但目前暫無權重系數設計和調節的理論解決方法，大多采用試驗法，其過程繁瑣[6-7]。為了解決權重系數設計和調整問題，文獻[8-11]采用模糊控制動態調節權重系數，但模糊控制規則的設計較為復雜。文獻[12-14]采用粒子群算法和神經網絡算法實現權重系數的調整，但需要構造大量訓練數據集且算法自身計算量較大。

設計無權重系數的MPTC也是解決方案之一。文獻[15-16]利用無差拍控制計算得到下一時刻的期望電壓矢量或定子磁鏈矢量，將磁鏈和轉矩轉換為同量綱的控制變量，但無差拍控制計算較為復雜。文獻[17]將磁鏈和轉矩轉換為相對誤差率，但如果存在含控制目標的參考值，如開關次數不確定，仍需設計權重系數。文獻[18-20]對各控制變量獨立排序，成本函數為無量綱的排序位置，但排序計算量較大。

改變成本函數結構形式是無權重系數路徑之一。文獻[21-22]將多目標成本函數加權求和形式轉換為單目標成本函數級聯形式，從而消除權重系數。文獻[23-24]將其轉換為單目標成本函數電壓矢量集合求交集形式。

本文建立PMSM并聯法MPTC，研究磁鏈控制電壓矢量集合和轉矩控制電壓矢量集合的電壓矢量個數對系統控制性能的影響，進一步建立考慮開關次數控制的并聯法MPTC，并采用模糊控制器動態調節開關次數，控制電壓矢量集合的電壓矢量個數。仿真結果驗證了PMSM并聯法MPTC可實現無權重系數，并可根據系統實時運行狀態動態調整控制目標集合電壓矢量的個數，優化系統控制性能。

1 PMSM MPTC

定子坐標系下，表面式PMSM磁鏈和轉矩預測模型如下所示：

(1)

(2)

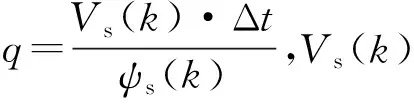
兩電平電壓源逆變器可產生8個開關狀態，對應備選電壓矢量集合如下所示：

Vs∈{V0,V1,V2,V3,V4,V5,V6}

(3)

式中：零電壓矢量V0可由開關狀態000或111生成，具體以開關次數最小原則選擇[24]。

PMSM MPTC成本函數如下所示：

(4)

PMSM MPTC系統將7個電壓矢量遍歷代入磁鏈和轉矩預測模型，得到下一時刻磁鏈和轉矩的預測值，再基于成本函數得到7個電壓矢量的控制效果，并選擇令成本函數最小的電壓矢量輸出，系統框圖如圖1所示。

圖1 PMSM MPTC系統

2 PMSM并聯法MPTC

由上文可知，由于磁鏈和轉矩的量綱不同，傳統PMSM需要設計和調整權重系數，而權重系數的設計與調整較為復雜。因此，將多控制目標成本函數加權求和形式轉換為獨立的成本函數電壓矢量集合求交集形式，可避免成本函數的設計與調整。

定義轉矩控制成本函數和磁鏈控制成本函數分別如下所示：

(5)

(6)

將7個電壓矢量遍歷代入轉矩模型和磁鏈模型，可得到下一時刻轉矩和磁鏈的預測值，再將其代入式(5)和式(6)，可分別得到7個轉矩控制成本函數和磁鏈控制成本函數。設轉矩控制電壓矢量集合VT有m個電壓矢量(1≤m≤7)，磁鏈電壓矢量集合VF有n個電壓矢量(1≤n≤7)。根據轉矩控制和磁鏈控制成本函數，從小到大依次對VT和VF分別輸出m個和n個電壓矢量。對VT與VF求交集，根據交集的情況輸出電壓矢量。如果VT和VF交集為空集，則輸出VT中磁鏈控制成本函數最小的電壓矢量。如果VT和VF交集非空集，則輸出交集中轉矩控制成本函數最小的電壓矢量。

PMSM并聯法MPTC算法流程圖和系統框圖分別如圖2和圖3所示。

圖2 PMSM并聯法MPTC算法流程圖

圖3 PMSM并聯法MPTC系統

基于MATLAB/Simulink建立PMSM并聯法MPTC系統仿真模型。仿真模型為離散模型，采樣周期為5×10-5s。直流母線電壓為312 V，轉速PI調節器參數為KP=50，KI=10，PI調節器輸出區間為[-30 N·m，30 N·m]。電機參考轉速初始為500 r/min，2 s時階躍至-500 r/min；負載轉矩初始為10 N·m，1 s階躍至-10 N·m，3 s階躍至10 N·m。仿真總時長為4 s。參考定子磁鏈幅值為0.3 Wb。仿真用PMSM參數如下：定子電阻Rs=0.2 Ω，定子電感Ld=Lq=0.008 5 H，永磁體磁鏈ψf=0.175 Wb，電機極對數p=4，額定轉速750 r/min，額定轉矩12 N·m，額定功率0.94 kW。

以m=n=3為例，PMSM并聯法MPTC仿真波形如圖4～圖6所示。

圖4 PMSM并聯法MPTC仿真的電機轉速

圖5 PMSM并聯法MPTC仿真的電機轉矩

圖6 PMSM并聯法MPTC仿真的定子磁鏈幅值

定義轉矩脈動均方根誤差(RMSE)和磁鏈脈動RMSE如下所示：

(7)

(8)

式中：n為采樣個數。

m=1,2,3…,7，n=1,2,3…,7，PMSM并聯法MPTC系統控制性能如表1所示。

表1 并聯法MPTC性能

基于式(4)建立傳統MPTC系統，相同權重系數下，經試驗法確定權重系數λ=50，此時電機系統控制性能如表2所示。

表2 傳統MPTC性能

由仿真結果對比分析可知：

(1) 隨著磁鏈集合電壓矢量個數的增加，轉矩脈動減小，磁鏈脈動增大；隨著轉矩集合電壓矢量個數的增加，轉矩脈動增大，磁鏈脈動減小。對于并聯法，增加某一控制目標集合電壓矢量的個數，則弱化對該控制目標的控制，該目標的控制性能變差。

(2) 當m+n>7，則VT與VF必定有交集，輸出交集中轉矩控制成本函數最小的電壓矢量，此時增加m對輸出的電壓矢量沒有影響。

(3) 當m=n=3，PMSM并聯法MPTC與權重系數等于50的傳統MPTC性能基本相當。

3 考慮開關次數的并聯法MPTC

對于PMSM MPTC，可將開關次數控制也作為其控制目標之一。如上文分析，當控制目標較多時，并聯法需確定各控制目標輸出電壓矢量集合并對電壓矢量求并集，計算量較大，故控制目標不宜過多。因此，本文將磁鏈和轉矩控制統一為性能控制，同時考慮開關次數控制，性能控制成本函數和開關次數控制成本函數分別如下所示：

(9)

gS=2×[|Sa(k)-Sa(k-1)|+|Sb(k)-

Sb(k-1)|+|Sc(k)-Sc(k-1)|]

(10)

式中：Sa(k)、Sb(k)和Sc(k)為備選施加電壓矢量對應開關狀態；Sa(k-1)、Sb(k-1)和Sc(k-1)為上一時刻開關狀態。

由式(10)可知，開關次數與備選電壓矢量、上一時刻開關狀態有關。備選電壓矢量集合如下所示：

Vs∈{V0,V1,V2,V3,V4,V5,V6，V7}

(11)

式中：V0和V7為零電壓矢量，分別對應開關狀態000和111。

由于兩電平逆變器開關狀態確定且有限，基于上一時刻的電壓矢量，備選電壓矢量的開關切換次數是已知確定的，如表3所示。因此，可根據上一時刻的電壓矢量，直接查表獲取8個電壓矢量對應的開關次數，無需計算。

表3 開關次數控制成本函數表

將8個電壓矢量代入式(9)可得到8個性能控制成本函數，基于上一時刻的電壓矢量和表3，可得到8個開關次數成本函數。根據性能控制成本函數和開關次數成本函數大小，從小到大對性能控制電壓矢量集合VC和開關次數電壓矢量集合VS分別輸出m個和n個電壓矢量，其中1≤m≤7，1≤n≤7。由表3可知，VS存在開關次數相同的情況， 因此n取值只有1、4、7、8四種情況。將VC與VS求交集，根據交集的情況輸出電壓矢量。如果VC和VS交集為空集，則輸出VC中性能控制成本函數最小的電壓矢量。如果交集非空集，則輸出交集中性能控制成本函數最小的電壓矢量。考慮開關次數的PMSM并聯法MPTC系統如圖7所示。

圖7 考慮開關次數的PMSM并聯法MPTC系統

上文相同仿真條件下，以m=3，n=4為例，考慮開關次數的PMSM并聯法MPTC仿真波形如圖8～圖10所示。

圖8 考慮開關次數后仿真的電機轉速

圖9 考慮開關次數后仿真的電機轉矩

圖10 考慮開關次數后仿真的定子磁鏈幅值

定義平均開關頻率如下所示：

(12)

式中：Nswitching為開關次數；t為仿真時間。

m=1,2,3,…,8，n=1，4，7，8，考慮開關次數的PMSM并聯法MPTC系統性能如表4所示。

表4 考慮開關次數的PMSM并聯法MPTC性能

基于下式建立傳統MPTC系統，相同權重系數下，經試驗法確定權重系數λ=0.005，此時電機系統控制性能如表5所示。

gC=gC+λ·gS

(13)

表5 傳統MPTC性能

由仿真結果對比分析可知：

(1) 隨著m的增加，開關頻率減小，控制性能變差；隨著n的增加，開關頻率增大，控制性能變好。

(2) 當m+n>7，則VC與VS必定有交集，輸出交集中性能控制成本函數最小的電壓矢量，此時增加m對輸出的電壓矢量沒有影響。

4 模糊并聯法MPTC

由上文可知，m和n的個數影響系統性能，可利用這一特征根據電機實時狀態動態調節m或n的大小，在磁鏈和轉矩脈動較大時，使系統側重提升控制性能，磁鏈和轉矩脈動較小時，使系統側重減小開關頻率，從而適應動態變化的電機運行狀態。

對于考慮開關次數的并聯法MPTC，VS的電壓矢量個數n只有1、4、7、8四種選擇，較為簡單，故選擇n作為動態調整變量。隨著n的增加，開關頻率增大，控制性能變好，采用模糊控制器動態調整n的大小，優化系統控制性能。由上文可知，m=3時，系統整體性能較好。因此，令m=3，由模糊控制器調節n。模糊控制器的輸入為轉矩誤差絕對值和磁鏈誤差絕對值，輸出為VS的n。轉矩誤差絕對值論域為[0 N·m, 2 N·m]，分為3個模糊子集{Ts,Tm,Tb}，隸屬度函數μ(T)如圖11所示。磁鏈誤差絕對值論域為[0 Wb, 0.02 Wb]，分為3個模糊子集{Fs,Fm,Fb}，隸屬度函數μ(F)如圖12所示。n的輸出論域為[0, 9]，分為4個模糊子集{n1,n2,n3,n4}，隸屬度函數μ(n)如圖13所示。

圖11 轉矩誤差絕對值隸屬度函數

圖12 磁鏈誤差絕對值隸屬度函數

圖13 VS電壓矢量個數n隸屬度函數

模糊控制規則如表6所示。經過Mamdani模糊推理規則后，采用最大隸屬度去大法解模糊并輸出;再采用最大隸屬度平均法解模糊并輸出。PMSM模糊并聯法MPTC系統如圖14所示。相同仿真條件下，PMSM模糊并聯法MPTC系統仿真結果如圖15～圖18所示。

表6 模糊控制規則表

圖14 PMSM模糊并聯法MPTC系統

圖15 模糊并聯法仿真的電機轉速

圖16 模糊并聯法仿真的電機轉矩

圖17 模糊并聯法仿真的定子磁鏈幅值

圖18 模糊控制器輸出n

當m=3，n=1，4，7，8和模糊調節n時，PMSM并聯法MPTC系統性能如表7所示。

表7 模糊并聯法MPTC系統性能

由仿真結果可知，模糊控制可根據轉矩和磁鏈誤差，動態調節開關次數電壓矢量集合個數，在誤差較大時，n較大，側重減小脈動；誤差較小時，n較大，側重減小開關頻率。和m=3、n=4相比，模糊控制性能較好，且可以減小定子磁鏈誤差峰值，開關頻率略有增大；與m=3、n=7和8相比，轉矩和磁鏈脈動有所增大，開關頻率較小。與權重系數等于0.005的傳統MPTC相比，轉矩、磁鏈脈動及開關頻率均有所降低。

5 結 語

(1) PMSM并聯法MPTC將多目標成本函數加權求和轉換為單目標成本函數電壓矢量集合求交集，從而消除權重系數。

(2) 對于并聯法，增大某一控制目標集合的電壓矢量個數，則弱化對該控制目標的控制，該目標的控制性能變差。

(3) 通過模糊控制動態調整控制目標集合的電壓矢量個數，可根據系統實時運行狀態，優化系統控制性能。相對于連續變化的權重系數，由于電壓矢量個數離散有限，模糊控制器設計簡單易行。