高中數學教師對“高觀點數學知識”的理解水平調查

單雪昀（新疆師范大學教育科學學院）

一、問題提出

“會當凌絕頂，一覽眾山小”對于高觀點下的初等數學來說意味著：要站得高、看得遠，才能將初等數學問題剖析得簡單明了。事實上，自菲利克斯·克萊因提出這一觀點后，中國的數學教育也在經歷著改革，最直觀可見的是高中數學教材新增以大學數學知識為背景的內容，選修教材居多。因此，研究高中數學教師的“高觀點數學知識”理解水平現狀是有必要的。下面以新疆地區高中數學教師和某大學數學教育方向研究生為測試對象，分成三個數學知識維度（如表1），擬從初等數學問題與大學數學“what”思想或方法有聯系的問題入手，探究新疆地區高中數學教師對“高觀點數學知識”的理解水平的現狀。

表1 數學知識維度具體特征

二、研究設計

1.研究對象

為方便調查師范類準教師與預備教師，針對準高中教師（新疆某大學數學教育方向研究生），以及新疆高中在職數學教師，包括新疆烏魯木齊市某高中教師、新疆南疆地區暑期國培班高中教師（2018年），采取分層抽樣方法，共計發放問卷40份，具體如表2、表3所示。

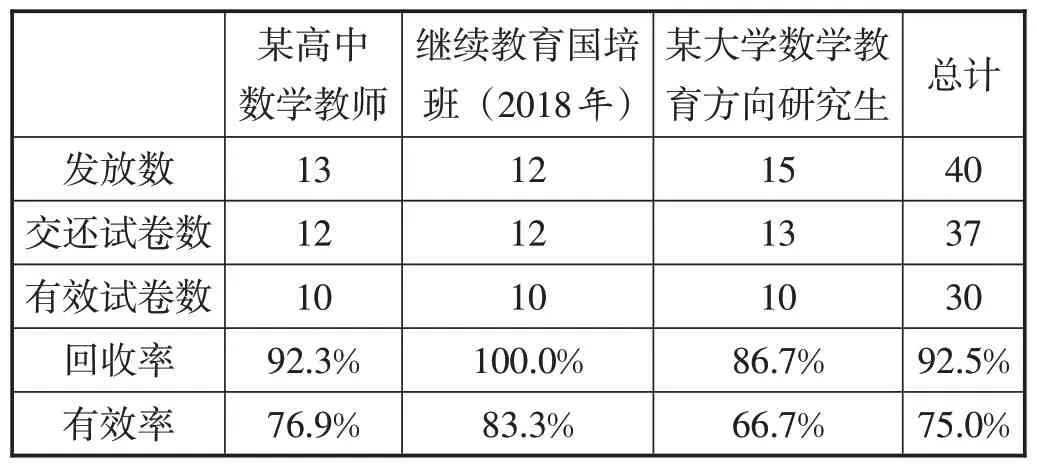
表2 試卷收集情況

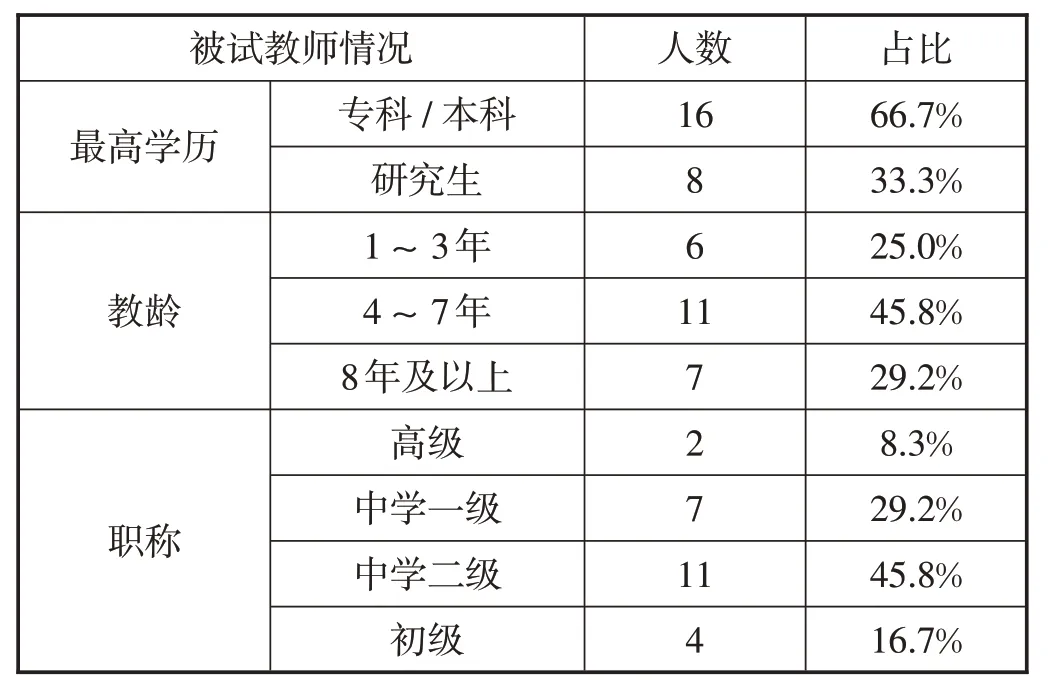
表3 被試教師信息分布情況

2.研究工具

（1）評價框架建構。

為建構合理的評價模型，將CIPP教育評價模型作為評價理論基礎，以研究問題“高觀點數學知識”為核心驅動目標，擬劃分三個理解水平維度：操作性、初概念性和探究性，如圖1、圖2所示。

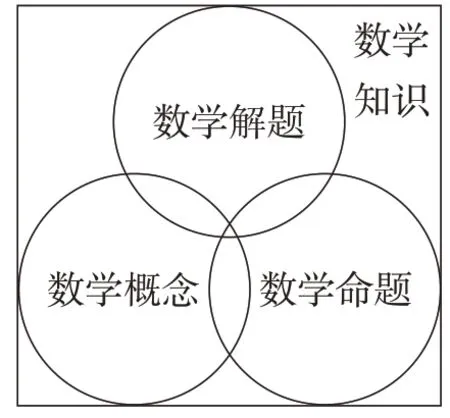
圖1 數學知識結構韋恩圖

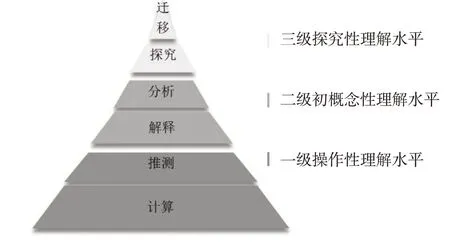
圖2 數學理解水平金字塔

這里針對圖2中數學理解水平的劃分標準進行解釋。一級操作性理解水平：教師知道數學的某個事實、概念與方法，但受制于數學教材的初等方法，僅能合情推理，缺乏數學宏觀意識。二級初概念性理解水平：教師了解數學概念、性質等，能演繹推理，但易犯循環論證而不自知，無法運用高觀點思想窺探初等數學本質。三級探究性理解水平：教師已具備初概念性理解，并能遷移大學數學方法揭示本質解決初等問題，進而縱橫地認識數學。

（2）“高觀點數學知識”水平測試卷。

測試內容選擇與確定考慮最基本問題，以《普通高中數學課程標準（2017年版）》為依據，將內容劃分為集合、函數與導數、三角函數與平面向量、數列與不等式、解析幾何、立體幾何與空間向量、統計與概率、其他部分，又基于彭翕成《從初等數學到高等數學（第1卷）》的觀點，將考查視角轉到初等數學教材本身，選擇函數與導數、數列與不等式、解析幾何、立體幾何與空間向量、其他部分（二項式定理）5個模塊重點考查。采用Microsoft Office Excel數據處理器對被試進行編碼錄入、匯總，運用SPSS數據軟件計算被試關于概念、命題、解題三個方面“高觀點數學認知”分別劃分探究性、初概念性和操作性層次水平并進行分析。

三、研究結果

1.“高觀點”數學概念理解水平

如表4，從數學問題的設計角度看，被測問題屬于常規且高頻問題，教師理應了解其背后的思想方法。

表4 “高觀點”數學理解水平占比表

具體而言，“高觀點”數學概念理解水平：探究性理解平均水平較其他數學維度的水平高出10%～18%，大部分教師“高觀點”意識高于實際水平。因此，在數學概念方面教師要注重強調對知識的理解與呈現，以看似合理的常識性問題為起點，脫離書本的桎梏，反向思維構建高等數學與初等數學的橋梁，再認識和解決初等問題。“高觀點”數學命題理解水平：呈現出被試的探究性和操作性理解水平極不穩定，而初概念及以上理解水平穩定在45%左右的狀態，差距大。因此，教師需打破長期教學方式表現的思維戀舊和循環邏輯定式錯誤，如“導數正（負）則單增（減）的演繹證明”不證自明等現象，逐步培養深度學習，重視并解讀學生每一次隱蔽性的數學語言。“高觀點”數學解題理解水平：處于初概念及以上水平的教師較之前兩個維度要高且穩定，操作性理解水平相對居多。尤其幾何和代數這類高考核心問題，教師俯瞰數學問題的廣度和深度相對較強，因此“高觀點數學知識”理解呈現較高水平。

2.“高觀點”數學問題實例分析

問題1：以52為例，解釋無理指數冪的含義。

這是人教B版《普通高中課程標準實驗教科書·數學1必修》中“基本初等函數（Ⅰ）”第一小節的內容。有4位教師直接類比正整數和分數指數冪的意義，認為“52=，即個5相乘”，曲解數學概念本質，認知水平較低；有16位教師較重視教材涉及的合情推理，從無理數“數”的角度做無限逼近，但欠缺具體、詳盡的演繹推理過程；有10位教師是以“數軸”為工具引出夾逼準則，利用不足近似和過剩近似數列逐次逼近，清楚解釋52的含義。

問題2：證明指數函數y=2x在(-∞，+∞)上是增函數（試給出每一步充分的推理依據）。

大多數教師在證明過程中極易陷入循環邏輯的怪圈：有21位教師回到單調性的定義，作差（作比），典型的循環論證，出現認知慣性；另有借對數的單調性逆推指數單調性，限定了自變量的取值范圍，違反一般性；僅有2位教師運用臺階法，將自變量從整數、有理數、無理數、有理數到無理數逐級證明（高數極限思想），符合大學數學的嚴謹性分析。

對于解題，如問題“若已知數列的前10項3，5，7，9，11，…，21，求數列的通項”，僅有不足15%的教師能正確運用拉格朗日插值公式解釋背后原理，其余教師只是通過觀察猜想公式；“求一組組合數之和”，不足25%的教師揭示教材C0n+C1n+C2n+…+Cnn=2n賦值±1的內涵。

四、總結與建議

1.數學概念

“廣度—深度”同步理解：數學概念本身具有高度的抽象性，對于概念教學，需要有意識地還原數學概念的數學化語言，即從學生理解的水平層次交代字面含義，結合“高觀點”認知，最大化地為學生的概念學習提高廣度，同時注意從具體簡單到抽象復雜的逐步延伸，進而促進學生明確概念、糾正錯誤，避免元認知導向錯誤。

2.數學命題

“內修—教學”雙向提高：要實現學生自我發現并創造數學知識，教師不應將整理好的證明直接提供給學生。教師自身的理解水平能夠達到引導和幫助學生進行“再創造”，組織自然生成的教學，學生自主完成命題的發現與證明。

3.數學解題

“創造—再創”一以貫之：以往教學注重問題解決方法上的“再創造”，但其實問題的本身更應注意，如增添數學的為什么，探尋源問題的路上層層揭開數學的神秘之紗。另外，還可以跳出數學符號化，將文學藝術與數學符號或思想連通，在問題的根源實現“再創造”，豐富數學的問題形式和解題視角，增添趣味。

五、結束語

解釋“數學概念”、證明“數學命題”、探究“數學解題”，無不告訴教師提高自身理解水平亟待加強，觀點高了，才能看得深。另外，師范類院校數學專業的學生更要從入校起重視聯系“高觀點”對初等數學的指導，避免教學斷層。