高中生解決不同情境物理問題能力的比較研究

梁 曉

（深圳實驗學校，廣東 深圳 518107）

物理學科核心素養注重培養學生的解決實際問題能力.《高中物理課程標準（2017年版）解讀》中的物理學科能力是指學習者對體現物理學科本質的真實問題情境的適應能力，即解決真實情境問題的能力.評價學生物理問題解決能力就是考查學生適應物理學科問題情境的能力，即學生能夠解決何種情境的什么層次的問題.［1］原始物理問題能真實檢測和訓練學生解決真實情境問題的能力，但學生日常訓練的多是模型化的傳統物理習題.近年來物理高考試題出現了大量以生產生活實際為背景的情景化物理問題.學生在不同情境下的物理問題解決能力的表現水平如何呢？本研究試圖從活動表現視角，借鑒PISA測評中問題解決能力的表現水平的劃分，建構物理問題解決能力的評價標準和表現水平框架，編制不同情境的物理問題，比較學生在不同情境下的物理問題解決能力.

1 物理問題解決能力的評價維度

1.1 基于情境的物理問題解決能力

物理問題解決的一般過程包括物理表述，物理應用和反思評價.這3個階段并非一個線性的流程，可能會交替出現；且物理問題解決的一般過程和問題解決能力不是一一對應的.因此，在評價學生的物理問題解決能力時，不能套用物理問題解決的過程來評價學生的物理問題解決能力.學生的心理過程具有內隱性，因此只能通過外顯的活動表現來判斷學生的物理問題解決能力.因此對于學生物理問題解決能力的評價應建立在真實的情境上，且命題設計時從情感教育的目標出發，利用真實情境和生活實際應用，讓學生在復雜的、開放性的真實情境中運用所學的物理知識解決問題.［2］

綜合考慮物理問題解決能力評價的科學性和可操作性，參照國內外的研究基礎和前面對物理問題解決能力的分析，［3－6］本研究中物理問題解決能力包括：物理表征能力、學科問題轉化能力、物理知識應用能力、數學推導能力，具體涵義如表1所示.

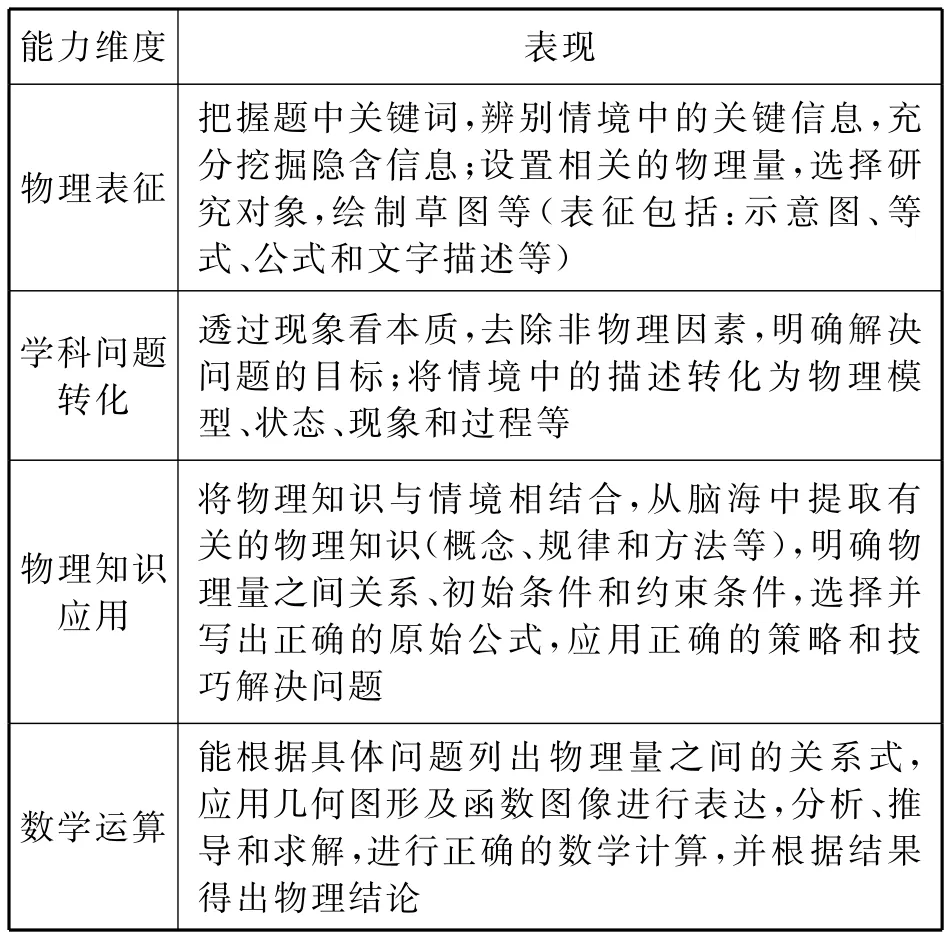
表1 基于情境的物理問題解決能力

1.2 物理問題解決能力的表現水平

本研究借鑒PISA2003和PISA2012問題解決測評中對問題解決能力的表現來描述物理問題解決能力的表現，通過評估學生的答案來觀察內隱的思維過程.［7，8］根據“物理表征”“學科問題轉化”“物理知識應用”和“數學推導”4個指標的內涵，將情境的復雜程度、知識和技能、思維方式的綜合程度等劃分為不同的水平（如表2）.每一級水平都包括了物理問題解決能力的4個維度，主要表現為學生在不同情境下應用物理概念和方法等解決物理問題的關鍵特征.

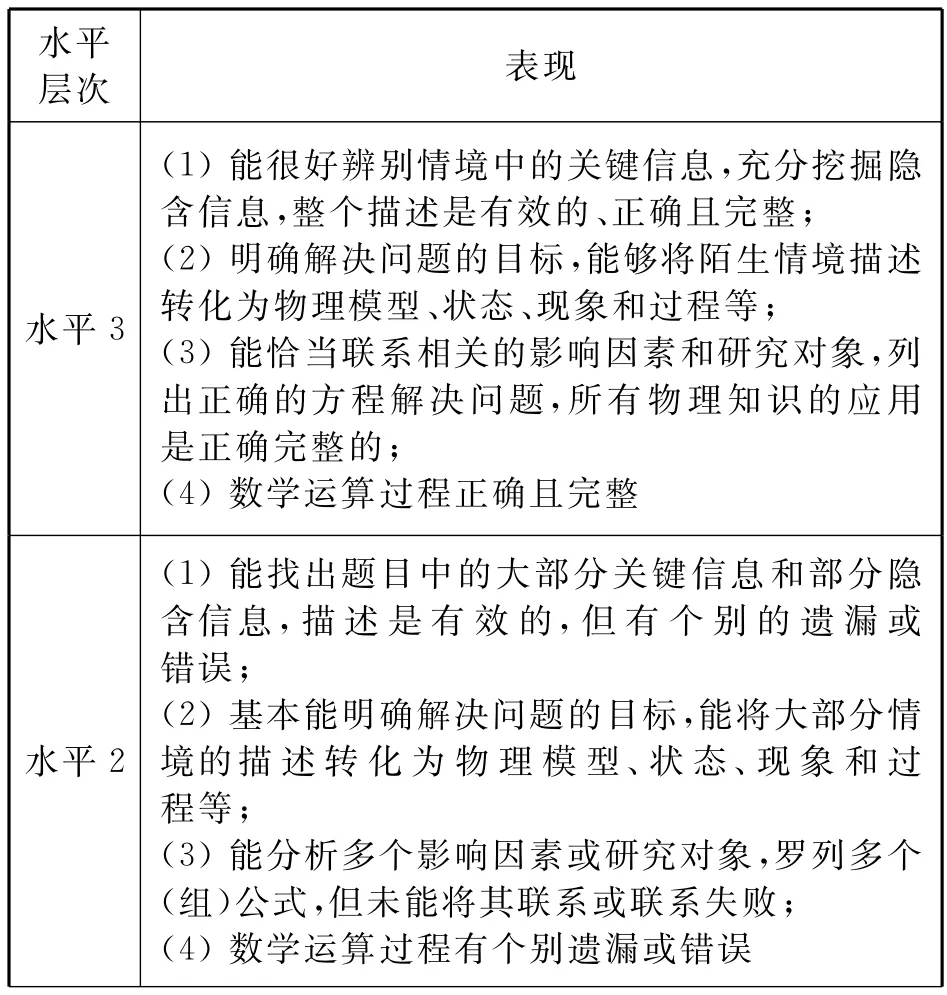
表2 物理問題解決能力表現水平

在實際操作中，為了更好評價學生物理問題解決能力，本文從整體上評價學生物理問題解決能力的水平，將物理問題解決能力的不同水平分別對應不同的分數，水平3、2、1、0分別對應3、2、1、0分.賦分過程中，由于學生的回答多樣，當學生的回答處于中間時，則以較低的水平進行賦分.

2 測試工具開發與施測

2.1 測試題開發

根據相關的文獻和標準，開發了3種基于“力與運動”主題的不同情境的物理問題：情境化物理問題（C）、原始物理問題（Y）和傳統物理習題（P）.［9－11］情境化物理問題和原始物理問題的情境源于生產生活現象，解答的過程需要學生設定一些簡單參數.每份測試卷中共有6道題，采用交叉設計，不同版本測試卷中的同一序號的題目情境不同，但所考查的知識點和解題的過程基本相同，具體分布如表3.

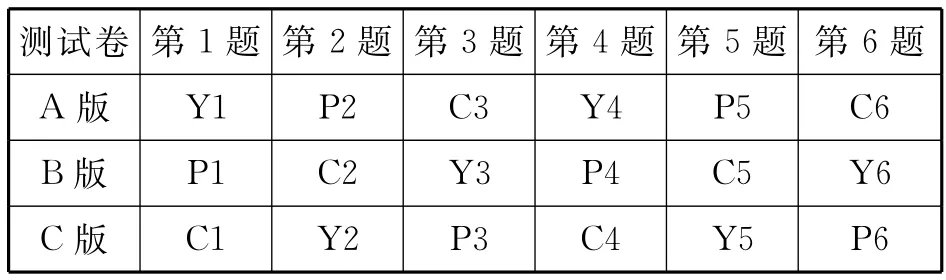
表3 各版本題目分布

為了提高測試卷的內容效度，邀請6名教師對測試卷進行檢查.建議教師以被試者的身份完成測試，判斷題目情境的選擇和描述、設問和題干是否清晰合理等，對不符合要求的題目進行修正后再施測.

2.2 質量評估

在高一年級4個班（重點班和平行班各2個）內隨機發放3個版本的測試卷，限時60分鐘完成.本次研究共發放200份測試卷，回收測試卷187份，有效問卷169份，含A版本52份，B版本55份，C版本62份.

2.2.1 評分者信度分析

本研究的測試題均是主觀題，學生的分數容易受到評分者主觀性的影響.因此采用經典測量理論的斯皮爾曼 布朗估計法計算評分者間信度.隨機抽取30份測試卷，其中包括A版本10份，B版本10份和C版本10份，由兩名評分者同時打分，利用SPSS軟件計算各題的斯皮爾曼系數如表4.每道題的斯皮爾曼系數均在0.01的水平上呈顯著性相關，說明根據所制訂評分標準賦分，所得到的數據一致性和可靠性較好，評分標準的可操作性較強.

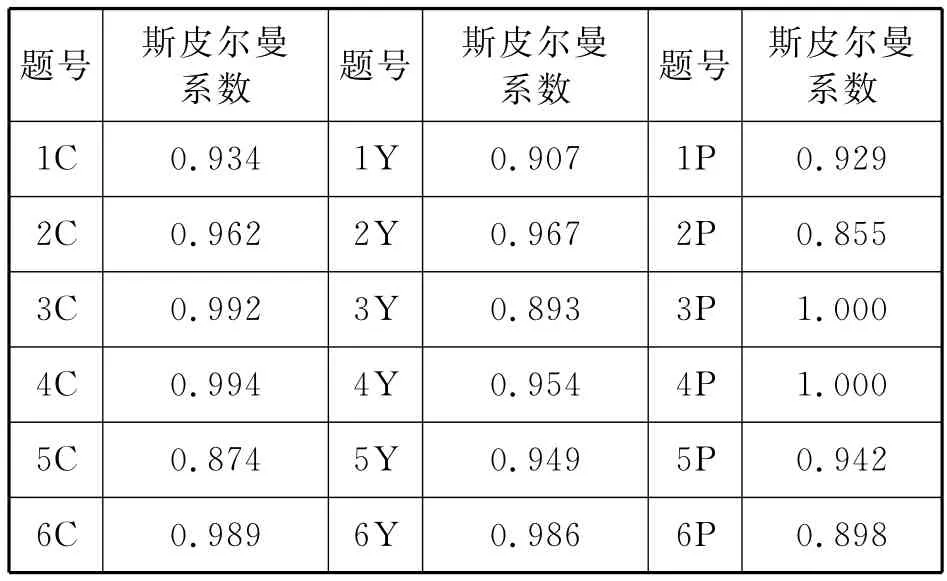
表4 各題目評分者信度統計表

2.2.2 效標效度分析

為了驗證測試題的有效性，將學生本次測試成績和期末考試成績做相關分析.學生本次測試的成績總分是18分，期末考試成績滿分是100分.將兩者的分數都進行歸一化統計，利用SPSS計算兩者相關系數如表5.結果表明學生的3個版本測試卷成績均與物理期末考試成績具有顯著性相關，說明該3個版本的測試卷能有效反映學生解決問題水平.

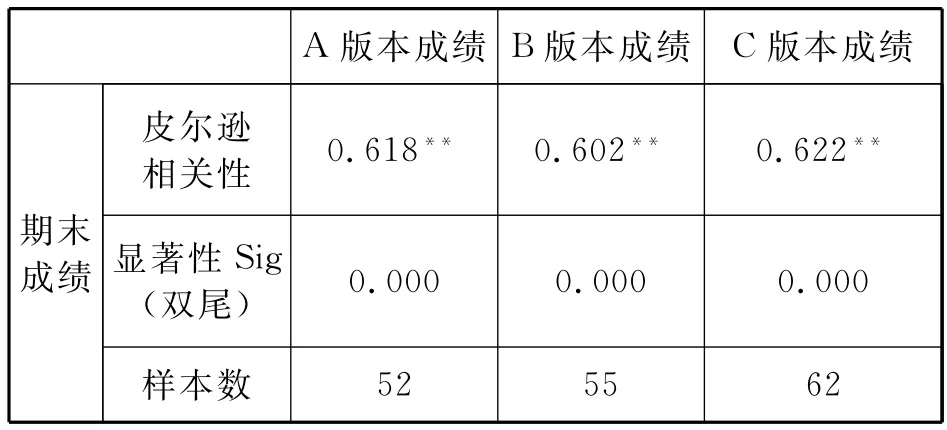
表5 學生本次測試成績與物理期末考試成績的相關性檢驗

3 高中生解決不同情境物理問題能力的比較研究

3.1 樣本學生的整體表現水平

每個學生所做的測試卷都會涉及原始物理問題、傳統物理習題和情境化物理問題各兩道，即每個學生的3個類型題目總分均為6分.按照題目的類型統計所有學生在每個類型問題中的平均分如下表6所示.從表中可看出學生解決傳統物理習題（P）的表現最好，解決情境化物理問題（C）中的表現略好，學生解決原始物理問題（Y）中的表現較差.

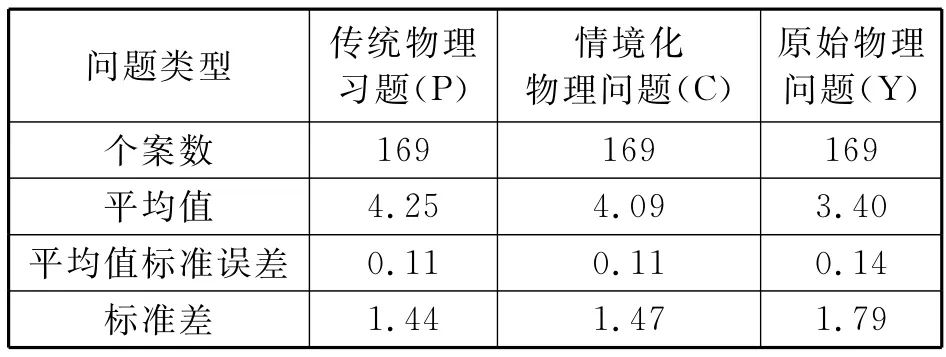
表6 學生在不同情境問題中的平均分

為了從整體上把握學生群體的總成績分布情況，將所有學生在各個題目中的總得分由低到高排列，進行分段統計，不同分數區間的頻率分布圖如圖1.

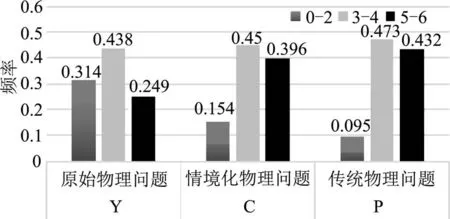
圖1 學生在各類型題目中的成績分布圖

從上圖可看出，學生解決情境化物理問題（C）和傳統物理習題（P）的表現相似，呈現右側高峰.學生解決原始物理問題（Y）的表現呈現中間高峰.從原始物理問題（Y）到情境化物理問題（C）再到傳統物理習題（P），成績處于0－2分的學生比例逐漸降低，成績處于5－6分的學生比例逐漸升高.可見在原始物理問題中處于中間“轉化”狀態的學生較多，而這部分學生在情境化物理問題和傳統物理習題中可能是以“專家”狀態出現.

3.2 學生解決不同情境問題的成績相關性和差異性

為了了解學生解決不同物理問題的成績的相關性，利用SPSS計算的Person系數對學生不同情境下的成績進行相關分析，如表7.結果表明學生的原始物理問題成績和情境化物理問題成績呈現弱相關，且學生的情境化物理問題成績與傳統物理習題成績呈現極弱相關性.

表7 不同情境問題成績的相關分析表

為了了解學生在不同情境下物理解決問題能力的差異性，利用SPSS的獨立樣本T檢驗分析學生解決不同情境物理問題的平均分差異，如表8和表9.從表中看出學生情境化物理問題（C）和原始物理問題（Y）的平均分具有顯著性差異（P＜0.05），說明學生解決情境化物理問題（C）的表現不能準確反映其解決原始物理問題（Y）的表現；但學生的情境化物理問題（C）和傳統物理習題（P）的平均分差異不顯著（P＞0.05）.

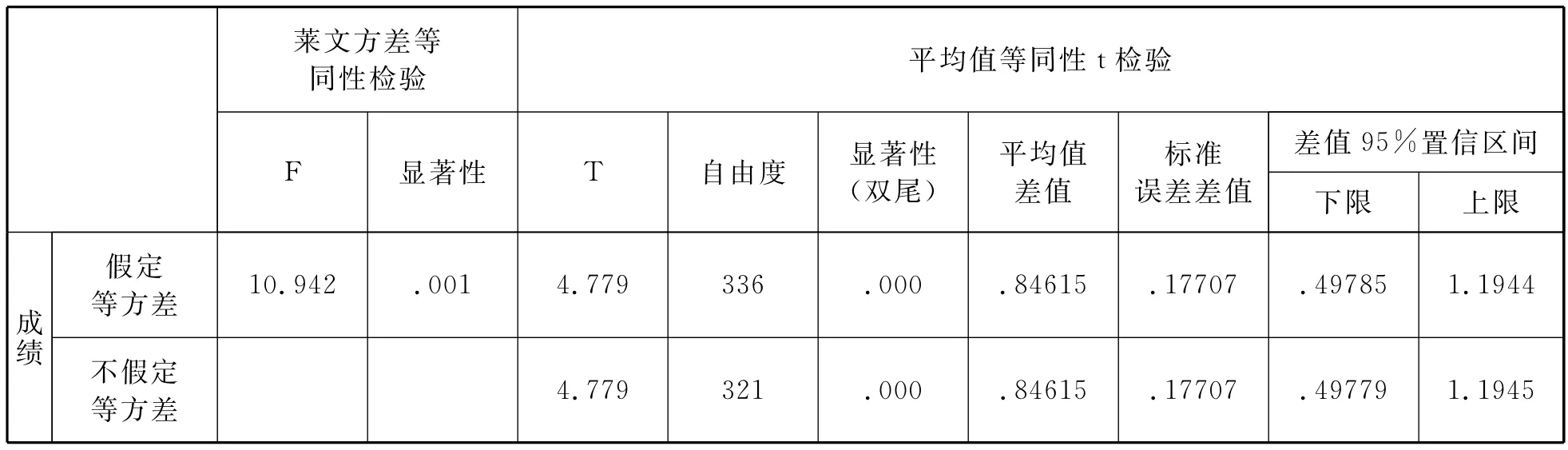
表8 Y類型和C類型的顯著性檢驗表

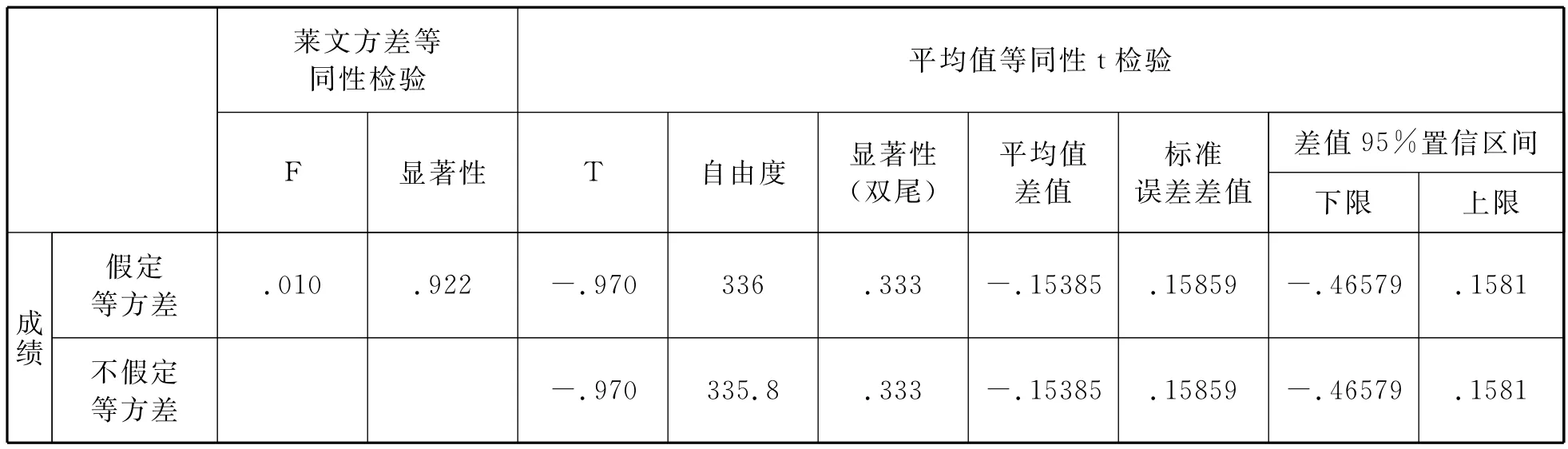
表9 C類型和P類型的顯著性檢驗表

3.3 學生解決不同情境問題的成績

3.3.1 傳統物理習題與情境化物理問題成績

將169名學生按照物理期末考試成績從高到低排名，其中排名前30%的學生為優生，排名處于30%－70%的學生為中等生，排名后30%的學生為弱生.圖2，圖3，圖4是不同層次學生的傳統物理習題（P）和情境化物理問題（C）成績的散點圖；其中橫坐標代表該學生的期末成績排名序號，縱坐標代表學生解決傳統物理習題（P）和情境化物理問題（C）的成績.

圖2 優生的傳統物理習題（P）和情境化物理問題（C）成績的散點圖

圖3 中等生的傳統物理習題（P）和情境化物理問題（C）成績的散點圖

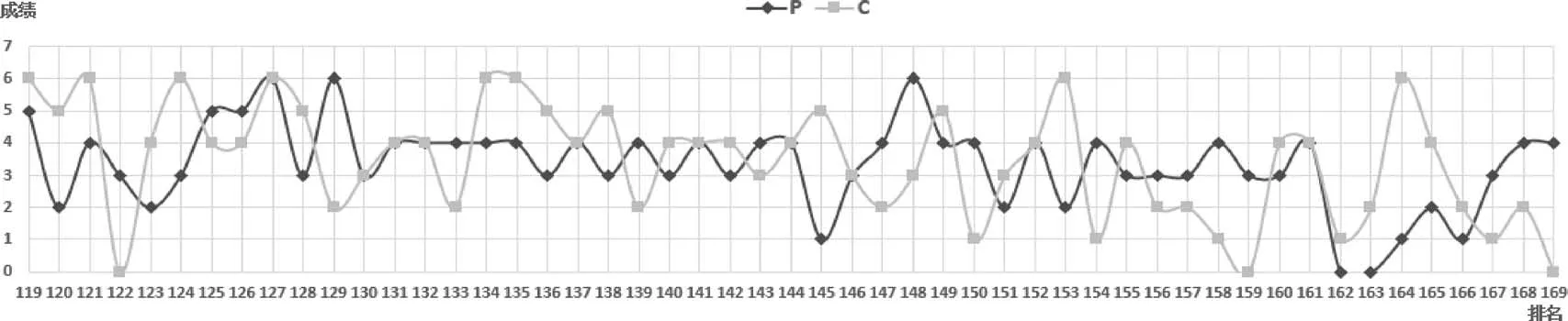
圖4 弱生的傳統物理習題（P）和情境化物理問題（C）成績的散點圖

從圖2、圖3、圖4中可看出學生解決傳統物理習題（P）成績的散點圖和情境化物理問題（C）成績的散點圖的變化趨勢不同.圖2表明前11%優生的傳統物理習題（P）和情境化物理問題（C）成績的散點圖均較穩定，振幅較小，說明這部分學生的物理問題解決能力的水平很高，能很好解決多種不同情境物理問題.圖3和圖4表明中下層次學生的傳統物理習題（P）和情境化物理問題（C）成績較不穩定，散點圖變化較大.可見問題情境對中等偏下成績的學生解決物理問題的影響較大.

3.3.2 原始物理問題和情境化物理問題成績

圖5，圖6，圖7是不同層次的學生的原始物理問題（Y）和情境化物理問題（C）成績的散點圖；其中橫坐標代表該學生的期末成績排名序號，縱坐標代表學生解決原始物理問題（C）和情境化物理問題（C）的成績.

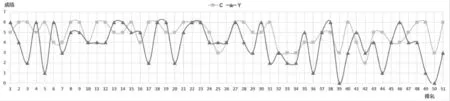
圖5 優生的原始物理問題（Y）和情境化物理問題（C）成績的散點圖

圖6 中等生的原始物理問題（Y）和情境化物理問題（C）成績的散點圖

圖7 弱生的原始物理問題（Y）和情境化物理問題（C）成績的散點圖

從圖5、圖6、圖7中可看出學生的原始物理問題成績（Y）的散點圖和情境化物理問題成績（C）的散點圖的變化趨勢不同.圖5表明前11%優生的傳統物理習題（P）和情境化物理問題（C）成績的散點圖均較穩定，振幅較小，說明這部分學生的物理問題解決能力的水平很高，能很好解決多種不同情境物理問題.圖6和圖7表明中下層次學生的傳統物理習題（P）和情境化物理問題（C）成績較不穩定，散點圖變化較大.

4 測評結論與討論

本研究在了解當前物理問題解決能力評價現狀的基礎上，借鑒國內外物理問題解決能力的評價標準和表現水平描述，制訂了物理問題解決能力的評價標準，并編制3種不同情境的物理問題測量學生的物理問題解決能力的水平，測評結果討論如下.

（1）學生解決傳統物理習題的表現水平最高，且解決情境化物理問題的表現水平比原始物理問題的表現水平高.部分學生面對真實情境的原始物理問題或情境化物理問題感覺無從下手，不能從情境中獲取與問題相關的信息，轉化物理問題，難以摒棄與解題無關因素的干擾，判斷出真實情境與哪些物理知識相關.因此不能很好根據解題需要假設相關變量，正確選擇物理知識和規律，建立知識與問題的聯系.這也反映學生的思維遷移能力不強，難以將物理概念和規律遷移到解決實際問題中.

（2）成績較好的學生解決不同情境問題的水平較為穩定，中等偏下的學生解決不同情境問題的水平波動較大.可見，問題情境對優生解決物理問題影響較小，對中等偏下學生的影響較大.這表明成績較好的學生的知識結構完整，在解決各種情境的物理問題時，能明確解決問題的目標，提取有效的信息解決問題.而成績中等偏下的學生對知識的理解較差，知識結構零散，對知識停留在簡單記憶階段，因此解決各種情境物理問題的能力較差.

（3）學生解決原始物理問題時對問題情境缺乏深入分析.原始物理問題由于未給出解決問題所需的物理變量，學生在解決原始物理問題的過程中缺乏對問題情境的深入和全面分析，容易受到題目表面特征（如某個物理術語）的影響.通過題目的表面特征映射到特定解決問題的方案，直接套用含有題目已知變量的物理公式或該術語的公式，并根據這個公式所需要的物理量由后往前推進而解決問題.

（4）學生利用草圖思考的水平有待提高.學生對問題的理解和表征是一個整體的思維過程，學生畫受力分析圖等是在理解題意的基礎上對物理模型的抽象.傳統的解題教學使部分學生形成了“畫圖—套公式—計算”的固定解題模式.一方面部分學生由于未能很好理解題目建立錯誤的物理模型，所畫的受力圖等不完整.另一方面，部分學生雖然能從題目提取有效的信息畫出正確的受力圖等，但學生的知識結構不深刻且對概念的理解不透徹，易陷入思維定式.對他們而言，畫草圖僅僅是一個做題的“形式工具”，并沒有真正起到輔助解決問題的作用.