大開口船型波浪彎/扭矩間接監測方法
范鑫楊, 李輝, 張猛, 曲先強
(1.哈爾濱工程大學 煙臺研究院,山東 煙臺 264000;2.廣東海裝海上風電研究中心有限公司,廣東 湛江 524000)
由于非大開口船型的抗扭剛度非常大,波浪扭矩對船體結構的影響較小,在非大開口船型波浪力矩間接監測時忽略了扭矩的影響。但對于集裝箱船等大開口船型而言,船體抗扭剛度較低,其所承受的波浪扭矩作用不可忽略[1]。
結構載荷的間接監測,即載荷識別,是結構力學中的反問題。載荷識別問題的研究源于20世紀70年代的航空領域[2],通過監測得到的結構響應反求飛機所受的外部動態載荷。從20世紀末,載荷識別技術逐漸應用到船舶結構載荷的間接監測中[3-4]。張猛等[5]提出了一種Tikhonov正則法與粒子群優化算法相結合的混合算法用于閘門冰載荷的反演,識別出了冰載荷的近似分布。Ritch等[6]對加拿大海岸警衛隊的破冰船的局部冰載荷進行了間接監測研究,通過監測得到的結構響應反求船體外板承受的分布式冰載荷。許勁松[7]提出了一種時域估測方法,從耦合的升沉,縱搖測量數據間接監測出船體垂向波浪彎矩值。梁文彬[8]研究了光纖光柵船舶結構健康監測系統的整體方案,并用雙光纖光柵實現了船體梁彎矩載荷的間接檢測。
Choi等[9]提出了一種在集裝箱船中部安裝長基線應變儀的船體應力監測系統的應變分解方法,該方法用線性矩陣方程表示,分解后的應變向量等于變換矩陣的逆與實測應變向量的乘積。通過在實際集裝箱船上的應用,證明是一種有效的求解集裝箱船彎扭力矩的方法。但該分解算法為半經驗半解析法,算法表達式簡單,缺乏理論依據。
由于大開口船型船體彎/扭聯合的復雜性,監測船體單一橫剖面特定位置的結構縱向應變很難準確計算出監測橫剖面所承受的波浪彎矩與波浪扭矩,本文提出了一種聯合雙剖面監測法,其數學模型基本形式通過結構彎/扭分析得到,計算精度通過全船有限元仿真驗證。
1 波浪彎/扭矩間接監測的數學模型
船舶在實際運營中或在海上航行時,其所承受的波浪彎/扭矩一般在船中附近最大,所以在監測波浪彎/扭矩時LVDT長基線應變儀一般布置在船中附近,其監測到的結構響應是2 m范圍內的結構平均微應變,對局部載荷不敏感,能更準確得到縱向應變。LVDT長基線應變儀監測到的結構縱向應變成分極其復雜,在監測船體波浪彎/扭矩時假定LVDT長基線應變儀監測到的結構縱向應變僅由波浪彎/扭矩引起。此外,船體扭矩一般包含2種成分,即自由扭轉扭矩和二次扭矩。在波浪彎/扭矩與結構縱向應變之間建立完整的映射關系之前需要明確各外力矩與結構縱向應變之間的關系。
1.1 總縱彎矩與結構縱向應變之間的關系
如圖1所示,在大開口船體艙段內安裝4支長基線應變儀LBSG_A、LBSG_B、LBSG_C和LBSG_D,其在局部坐標系下的坐標分別為(yA,zA)、(yB,zB)、(yC,zC)和(yD,zD)。局部坐標系的原點與結構橫剖面的形心位置相同,如圖1所示。在此定義,能使船體結構向上拱起,即向Z軸正向拱起的總縱彎矩MV為正,反之為負。
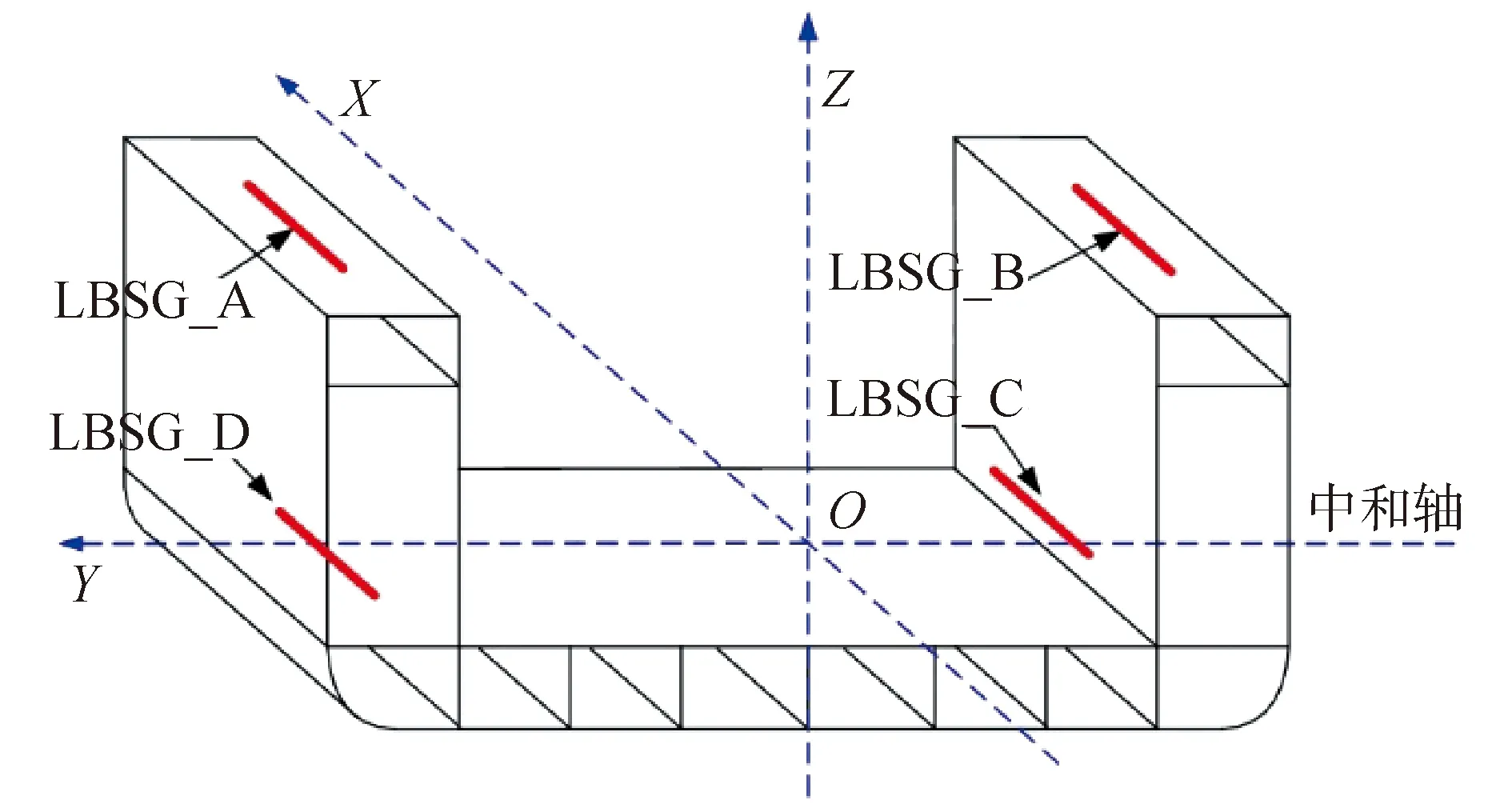
圖1 長基線應變儀布置Fig.1 Arrangement of long base strain gauges
若此船體艙段僅承受總縱彎矩MV的作用,由純彎曲假定,很容易得到總縱彎矩MV與4支長基線應變儀安裝位置處的結構縱向應變之間的線性關系:
(1)
式中:E為彈性模量;Iy為船體橫剖面對Y軸的慣性矩。
1.2 橫向彎矩與結構縱向應變之間的關系
在此定義,能使船體結構向左舷拱起,即向Y軸正向拱起的橫向彎矩MH為正,反之為負。若此船體艙段僅承受橫向彎矩MH的作用,由純彎曲假定,很容易得到橫向彎矩MH與4支長基線應變儀安裝位置處的結構縱向應變之間的線性關系:
(2)
式中Iz為船體橫剖面對Z軸的慣性矩。
1.3 自由扭轉扭矩與結構縱向應變之間的關系
自由扭轉也稱為圣.維南扭轉,即結構在扭轉過程縱向應變不受約束。根據結構剖面形式,結構剖面可分為開口、閉口以及混合等3種主要結構形式。集裝箱船等大開口船型一般為多閉口結構。由于正多邊形結構在扭轉過程中橫剖面沒有翹曲正應力,即正多邊形結構所承受的扭矩僅含有自由扭轉扭矩一種成分,所以為簡要說明自由扭轉扭矩與結構縱向應變之間的關系,以圓筒形結構的扭轉為例,如圖2所示。
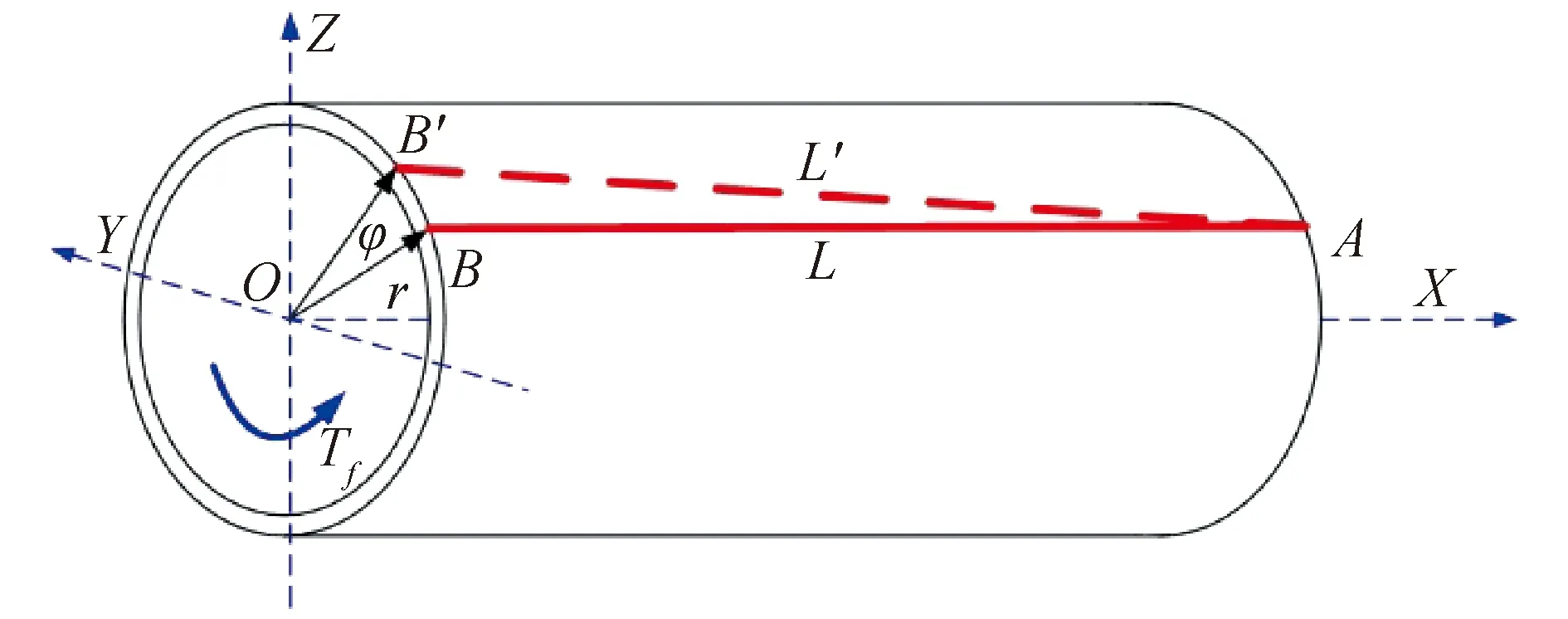
圖2 結構自由扭轉Fig.2 Structural free torsion
圖2所示的圓筒形結構右端剛性固定,左端僅有扭矩Tf作用。圓筒形結構橫剖面的扭心(扭轉中心)與其形心重合,如圖2中的O點。長基線應變儀通過基座安裝與A、B2點,用于測量圓筒形結構外表面的一條縱向“纖維”AB的長度變化量。在扭矩Tf作用前,AB的長度為L,扭矩Tf作用后,B點變化至B′,AB′的長度變為L′,左端剖面扭角為φ,扭轉半徑,即長基線應變儀距扭轉中心的直線距離為r。所以,長基線應變儀的監測應變可表示為:
(3)
進而得到:
(4)
船體結構的縱向應變一般可認為是微量,所以:
(5)
最終,自由扭轉扭矩與縱向應變之間的關系可表示為:
(6)
式中:G為剪切模量;J為結構橫剖面自由扭轉慣性矩。
類似,若船體艙段僅承受自由扭轉作用,如圖3所示。大開口船型的橫剖面扭心一般位于船體基線以下,如圖3中的O點。4支長基線應變儀與扭心O的直線距離分別為rA、rB、rC和rD,則自由扭轉扭矩Tf與結構縱向應變之間的關系可表示為:
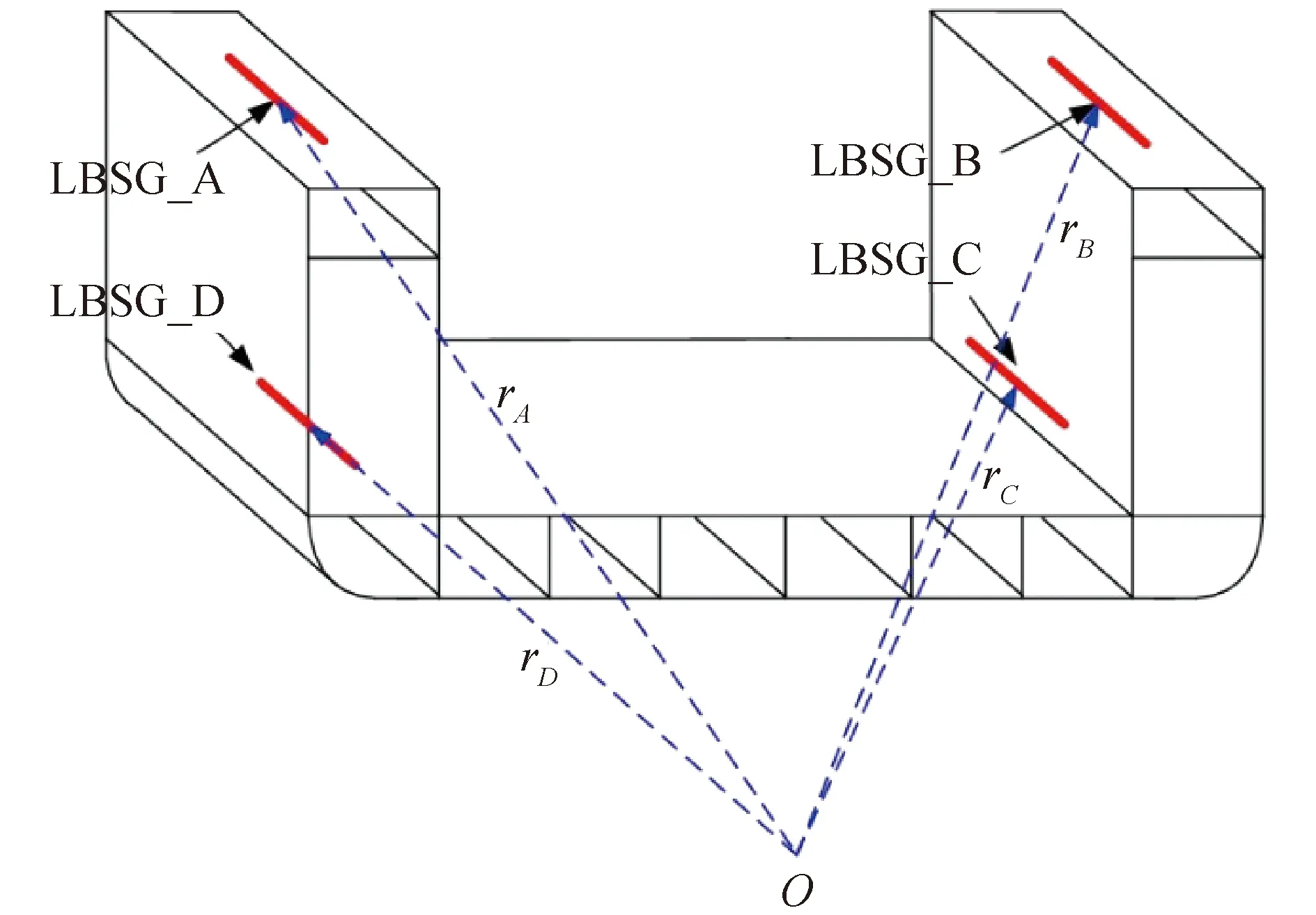
圖3 船體結構自由扭轉Fig.3 Free torsion of hull structure
(7)
1.4 二次扭矩與結構縱向應變之間的關系
船體扭矩一般為自由扭轉扭矩和二次扭矩的和,其在大開口貨艙區的近似分布如圖4所示。
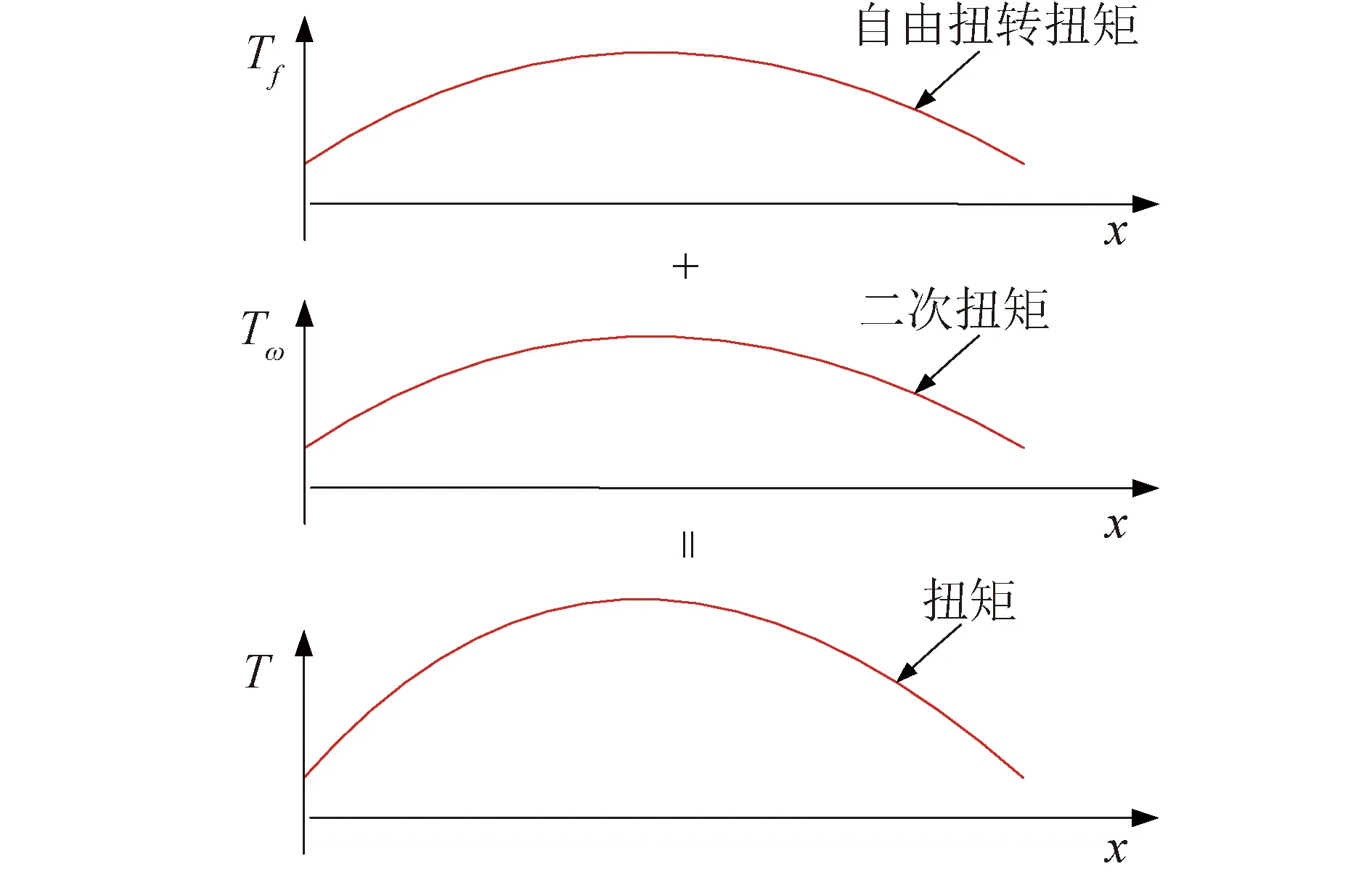
圖4 船體扭矩成分Fig.4 Component of hull torque
二次扭矩Tω為雙力矩B的導數,即:
(8)
二次扭矩Tω和雙力矩B在大開口貨艙區的近似分布如圖5所示。
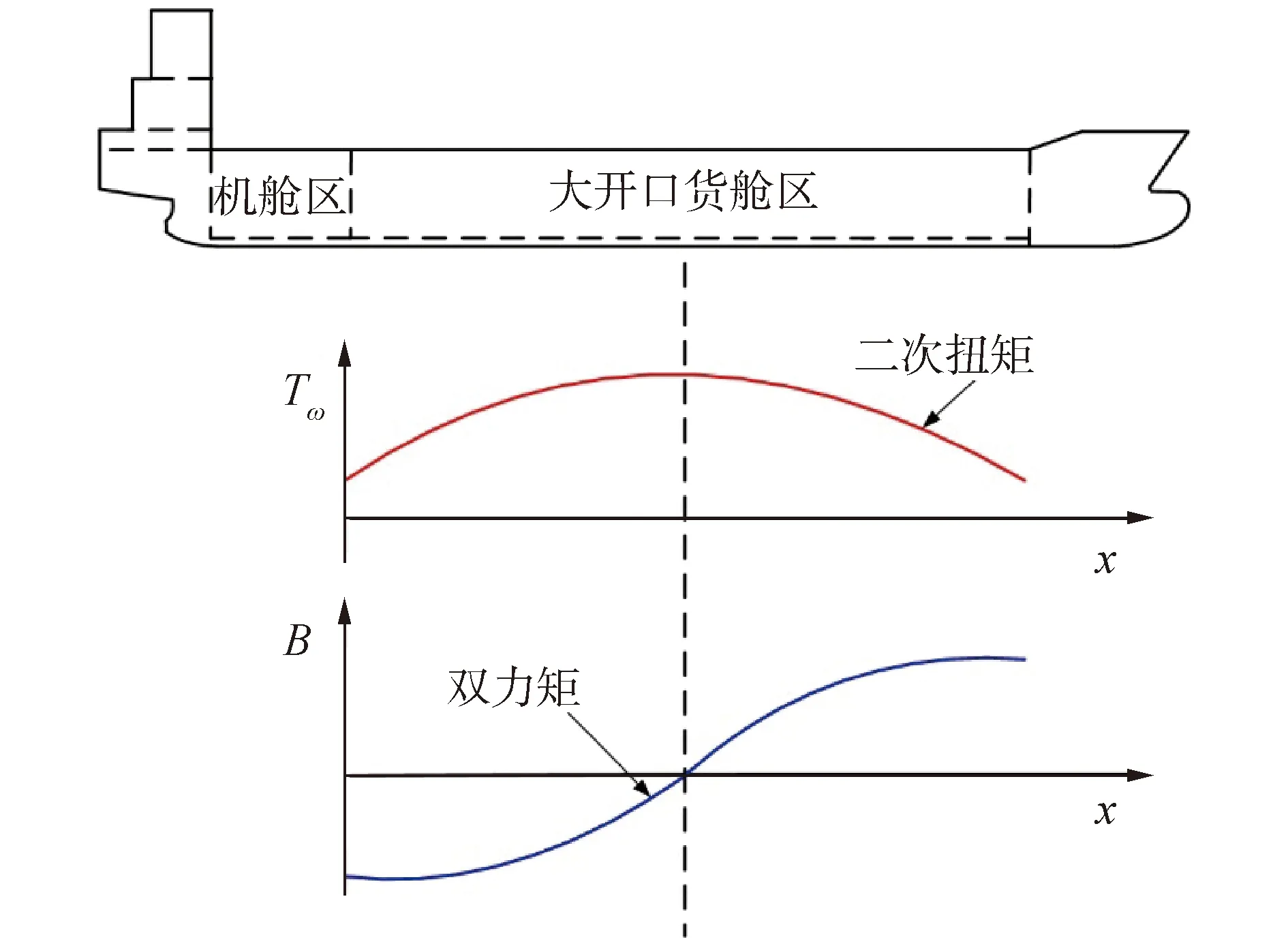
圖5 雙力矩與二次扭矩Fig.5 Bimoment and warping torque
若大開口艙段僅受二次扭矩Tω作用,二次扭矩Tω與長基線應變儀安裝位置處的結構縱向應變并無線性關系,而雙力矩B與結構縱向應變存在線性關系:
(9)
式中:ε為長基線應變儀安裝位置處的結構縱向翹曲應變;ω為長基線應變儀安裝位置處結構扇性坐標;Iω為船體結構橫剖面的扇性慣性矩。
1.5 波浪彎/扭矩間接監測的數學模型
若某一大開口艙段同時承受總縱彎矩MV、橫向彎矩MH、自由扭轉扭矩Tf和雙力矩B的作用,則傳感器安裝位置處的結構縱向應變可由線性疊加得到:
ε4×1=K4×4·f4×1
(10)
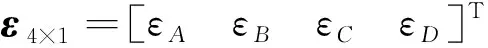
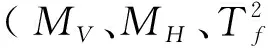
(11)
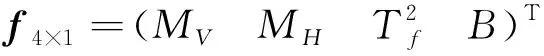
明顯,式(10)是一個靜定數學模型,即已知物理量和未知物理量的數量相同。為提高監測結果的精度和穩定性,長基線應變儀的合理數量一般做上浮50%~100%的處理。考慮成本和精度問題,在船體監測橫剖面內安裝6支長基線應變儀,則數學模型可以表示為:
(12)
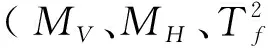
綜上所述,單一船體橫剖面監測的數學模型可簡化表示為:
εn×1=Kn×4.f4×1
(13)
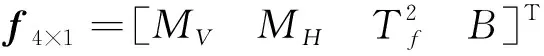
綜上可知,長基線應變儀安裝位置處的結構縱向應變向量εn×1可通過監測得到,傳遞矩陣Kn×4可根據力學原理逐一計算各元素得到。在已知εn×1和Kn×4的情況下,外力矩向量f4×1可由直接求逆法或Moore-Penrose逆法得到。但是,外力矩向量f4×1中不包含二次扭矩Tω,進而無法得到船體監測橫剖面的扭矩大小。二次扭矩Tω為雙力矩B的斜率或導數,所以可通過聯合雙剖面監測近似得到二次扭矩Tω。聯合雙剖面監測是指對兩個鄰近的船體剖面進行監測,然后用兩監測橫剖面的計算結果近似逼近中間剖面的外力矩結果,如圖6所示。

圖6 聯合雙剖面監測Fig.6 Structural monitoring in double section
若在鄰近的2個監測橫剖面內各布置6支長基線應變儀,則監測橫剖面的數學模型可簡化表示為:
(14)
監測橫剖面的外力矩向量為:
(15)
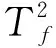
(16)
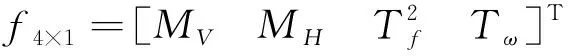
將式(15)代入式(16)得:
(17)
式(17)為聯合雙剖面監測的數學模型,得到f4×1之后即可近似得到中間剖面的總縱彎矩MV、橫向彎矩MH和扭矩T=Tf+Tω。
大開口船型(如集裝箱船)橫剖面的扇性坐標的分布形式一般如圖7所示,即關于船體橫剖面對稱線對稱。明顯,此類大開口橫剖面一般存在6個扇性坐標零點。雙力矩引起的結構縱向應變可表示為ε=Bω/EIω。所以,在扇性坐標零點處,即ω=0時,雙力矩不會引起結構縱向應變。因而,長基線應變儀或其他監測船體縱向應變的傳感器安裝時應避開扇性坐標零點,盡量安裝在扇性坐標值較大的位置,如舷側上部、頂部以及舭部等位置。

圖7 橫剖面扇性坐標Fig.7 Fan-shaped coordinate of hull section
2 某集裝箱船簡化模型
船舶水動力模型如圖8所示,其中入射波方向間隔為45°。
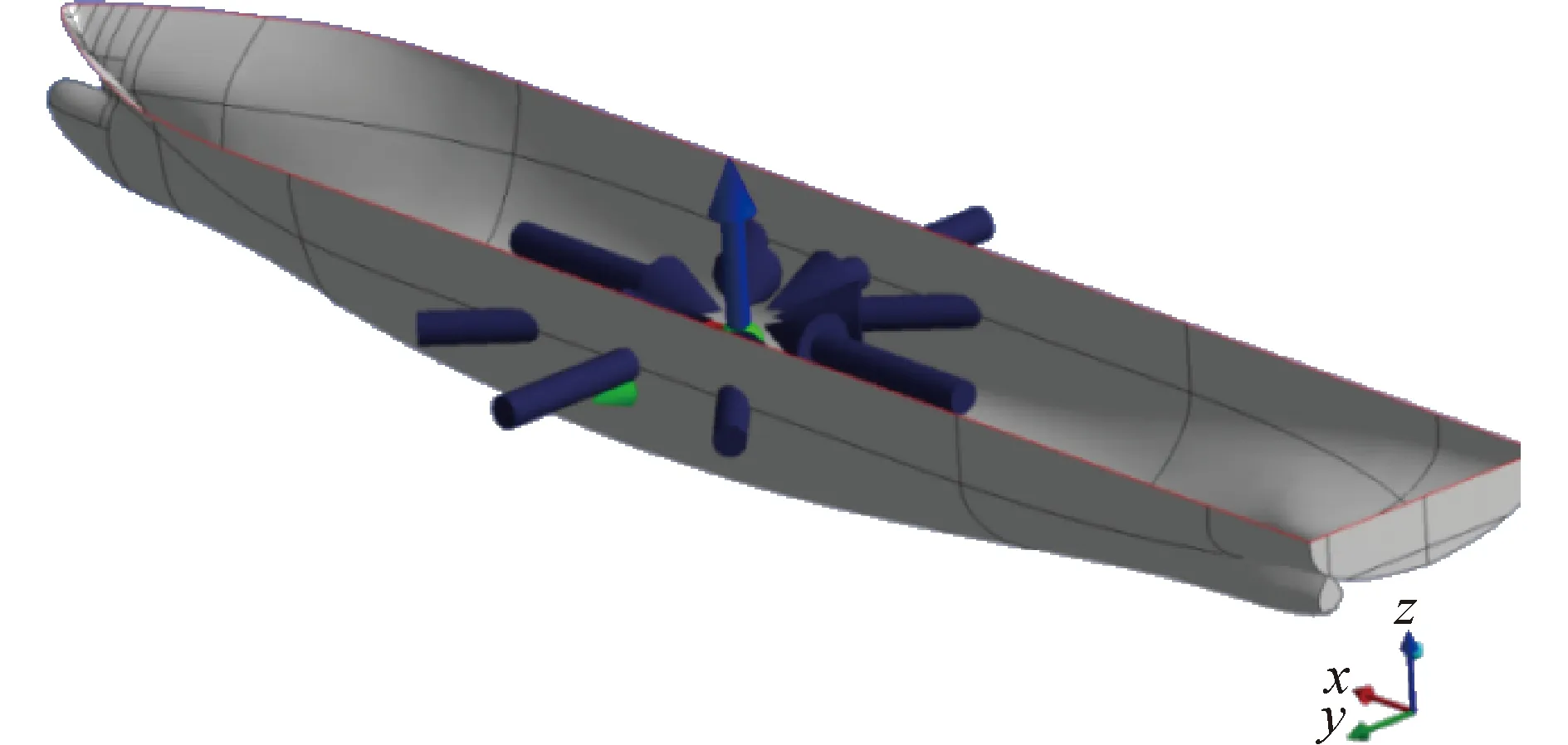
圖8 船舶水動力模型Fig.8 hydrodynamic model of ship
船舶水動力模型的單元總數為33 729,其中濕表面單元數,即水線面以下的單元數為21 442。船體結構有限元模型如圖9所示。

圖9 船體結構有限元模型Fig.9 Finite element model of hull structure
頻域波浪載荷計算時,頻率范圍為0.02~0.3 Hz,平均內插69個頻率點,共計71個頻率點,計算結果如圖10所示。圖10所示為波浪入射角為45°,頻率為0.104 Hz,相位角為-38.9°,波幅為2.5 m的計算結果。
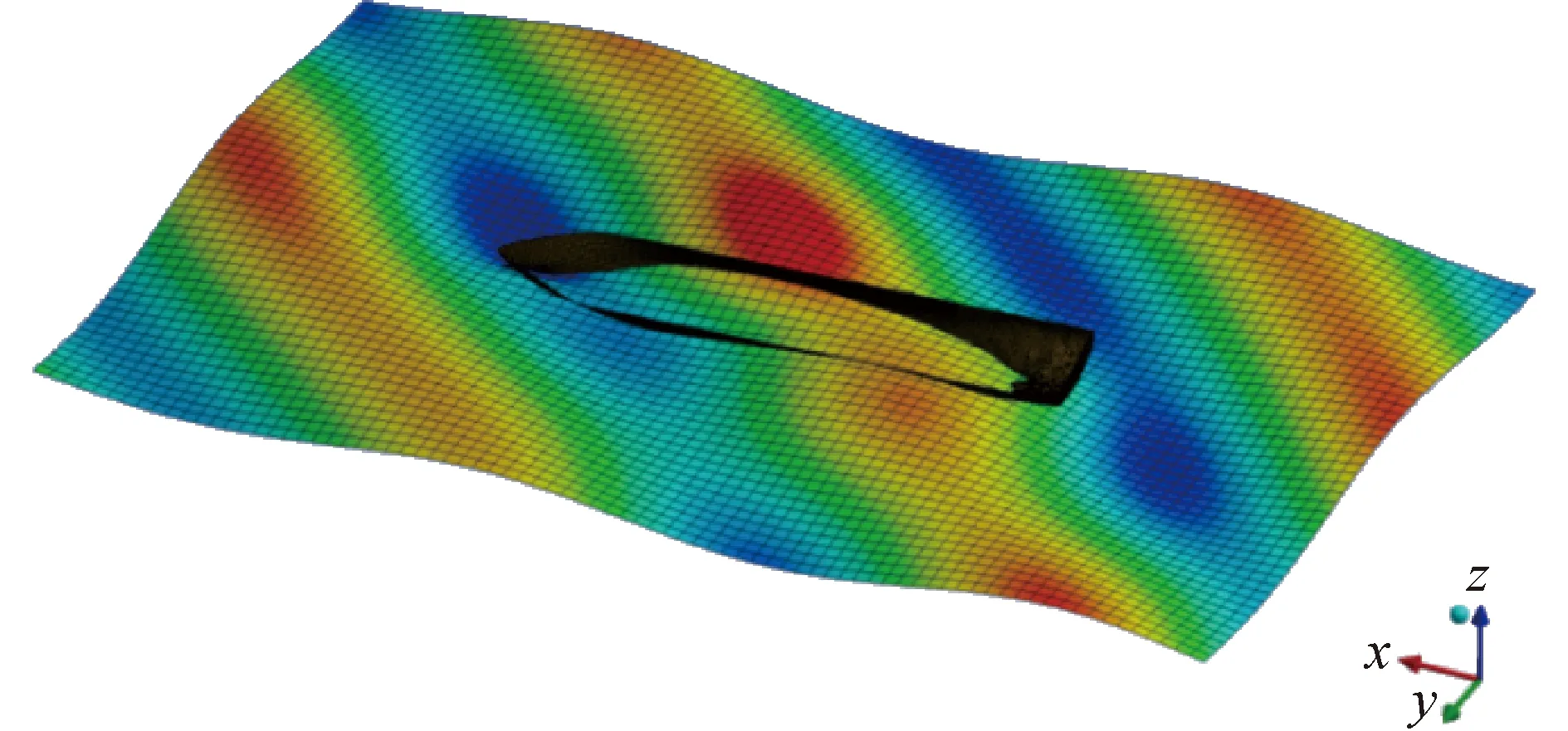
圖10 水動力計算結果Fig.10 Hydrodynamic results
對應某入射波方向、頻率、相位角和波高的船體濕表面的波浪面壓力可由AQWA-WAVE模塊導出,然后在經典ANSYS中加載到結構濕表面并計算結構響應。由于水動力模型和結構有限元模型的單元不一致,所以波浪載荷通過映射方式加載,如圖11所示。

圖11 波浪載荷加載Fig.11 Loading of wave load
3 彎/扭矩間接監測方法的有限元仿真驗證
在彎/扭矩間接監測方法的有限元仿真驗證中,假定長基線應變儀的安裝位置如圖12所示。長基線應變儀關于船體中縱剖面對稱設置,所以在每個監測橫剖面內安裝6支長基線應變儀。
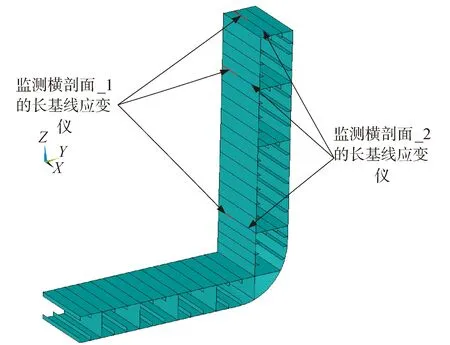
圖12 長基線應變儀安裝Fig.12 Arrangement of long base strain gauges
圖12所示的傳感器布置方案所對應的數學模型如式(17)所示。式(17)中的剖面慣性矩Iy和Iz、自由扭轉慣性矩J、扇性慣性矩Iω、橫剖面扭心坐標等可由COMPASS軟件直接計算出,進而可得到長基線應變儀與扭心的距離rA~rF。但是,長基線應變儀安裝位置處的扇性坐標值ωA~ωF需要通過數值法另行計算。
得到數學模型之后,其反求精度的驗證過程與波浪彎矩間接監測的驗證過程一致。此外,大開口船型在斜浪航行時所承受的波浪扭矩幾乎達到最大,故在驗證數學模型反求結果精度時僅以斜浪航行為例,即波浪入射角為45°。2 m波高時的波浪彎/扭矩反求結果如圖13所示。

圖13 波浪入射角β為45°時間接監測結果(2 m波高)Fig.13 Indirect monitoring results when wave incident angle is β=45°(2 m wave height)
由圖13可看出,波高2 m時,總縱彎矩MV和橫向彎矩MH的反求結果精度較高,總縱彎矩MV峰值誤差約在5%,橫向彎矩MH峰值誤差約在9%。但是,扭矩T的反求結果誤差較大,峰值誤差約在30%。4 m波高時,波浪彎/扭矩反求結果如圖14所示。
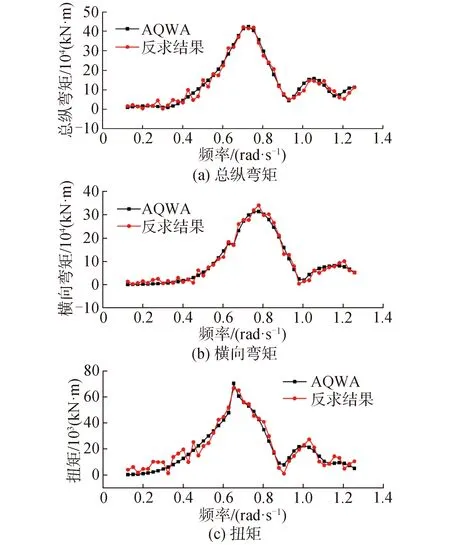
圖14 波浪入射角β為45°時的間接監測結果(4 m波高)Fig.14 Indirect monitoring results when wave incident angle is β=45° (4 m wave heigh)
從圖14中可以看出,波高4 m時,總縱彎矩MV和橫向彎矩MH的反求結果精度較高,總縱彎矩MV峰值誤差約在2%,橫向彎矩MH峰值誤差約在9%。此外,扭矩T的反求結果的精度基本可以接受,峰值誤差約在6%。對比波高2 m和波高4 m的反求結果可看出,載荷較大時反求精度一般較高,載荷較小時反求精度一般較低。
4 結論
1) 大開口船型斜浪中航行時易受波浪扭矩作用且大開口船型抗扭剛度偏低,針對此特點,基于船體扭轉基本原理提出了一種根據船體結構縱向應變反求監測橫剖面波浪彎/扭矩的方法,即聯合雙剖面監測法。
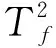
3) 通過有限元仿真算例驗證了聯合雙剖面監測法的有效性,結果表明,聯合雙剖面監測法基本能夠準確地反求出波浪彎/扭矩,尤其是載荷較大時。

