基于序貫平差的沉降預測模型高效更新方法
鄭一帆,于先文
(東南大學 交通學院,江蘇 南京 211189)
不均勻沉降是導致建構筑物開裂、塌陷等結構性破壞的主要原因之一,嚴重影響建構筑物的服務性能,威脅其安全性與穩定性[1]。沉降預測是目前大多數工程進行地基處理的主要依據,其預測結果與工后不均勻沉降的處理效果密切相關。沉降預測分為兩個步驟,首先使用工程的實測沉降數據建立沉降預測模型,然后通過沉降預測模型預測工后沉降。隨著工程進展,沉降預測模型需要不斷地更新來保障預測的質量。對于高鐵、大型橋梁等時間跨度大的工程項目,建立一個沉降預測模型高效更新的方法具有重要的意義。
目前,沉降預測模型的更新普遍采用簡單的傳統更新方法。在實際的工程中,廣泛使用的模型如雙曲線法模型[2-4]、指數曲線法模型[4-6]、星野法模型[8-9]等都使用傳統最小二乘方法進行模型更新。該方法的具體過程為:新增觀測數據后,利用全部數據列出誤差方程進行最小二乘間接平差,得到新的沉降預測模型系數。即便被廣泛應用于實際工程中,傳統更新方法也仍存在不足之處,具體表現為以下三點:①數據存儲量大,需要將歷史沉降數據全部保存,歷史沉降觀測數據重復地參與擬合過程;②模型更新計算量大,每次更新過程都需要使用到所有的沉降數據,計算過程中的矩陣維數可能會非常高;③存在數據損失風險,由于歷史數據數量龐大,可能存在數據丟失、被篡改、誤錄入等現象,對預測模型的正確更新帶來風險。
針對傳統更新方法所存在的這些問題,本文將序貫平差理論[10-12]應用到沉降預測模型更新的領域,導出詳細計算流程和相關系數算法,以避免歷史數據的存儲,有效提高模型更新效率,并通過工程算例驗證新方法的正確性和高效性。
1 模型的傳統更新方法
不同沉降預測模型的方程有一定的差別,但包括雙曲線法模型,指數曲線法模型,星野法模型在內的絕大多數模型可以表達為統一的二維線性形式,其表達式為
y=a0+a1×f(t)
(1)
式中:a0、a1為模型系數;t為觀測時間;y為包含t時刻沉降信息的因變量,為便于表達,下文直接用沉降觀測量指代。
在獲取第n+1期新觀測的沉降量yn+1后,使用傳統的更新方法對沉降預測模型進行更新。首先利用全部n+1期沉降數據列出n+1維的誤差方程組
V=Aa(n+1)-Y
(2)
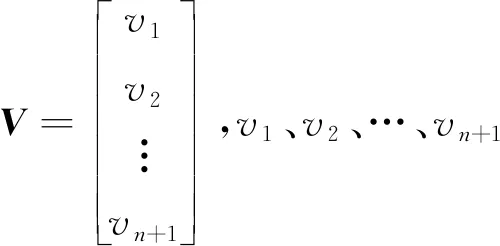
利用最小二乘法可得系數矩陣的估值
(3)
式中:P為觀測值的權矩陣,其確定方法可參考文獻[16]。
根據式(3)可得更新后的沉降預測模型為
(4)
計算預測模型的相關系數為
(5)
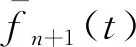
傳統更新方法算法簡單,但是隨著觀測時期的延長,沉降觀測數據的不斷增加,誤差方程組的擴充降低了計算的效率。同時,歷史觀測數據轉抄等過程中可能發生錯漏,大量存儲的歷史觀測數據增加了模型更新發生錯誤的風險。
2 基于序貫平差的模型高效更新方法
2.1 高效更新方法
序貫平差方法的核心思想是利用前期平差結果和當前觀測數據進行逐次平差[10],在測量的多個領域已有成功的應用[13-15]。為改善傳統更新方法的缺陷,將序貫平差理論引入沉降預測模型更新過程中,以得到模型高效更新方法。
基于前m(m≥2)期數據,利用最小二乘法首次得到沉降預測模型為
(6)
以及首個系數向量估值的權陣為
W(m)=ATPA
(7)
自m+1期起,即可利用序貫理論進行模型更新。下面以第n+1(n≥m)期數據為例,導出沉降預測模型高效更新計算公式。
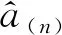
(8)
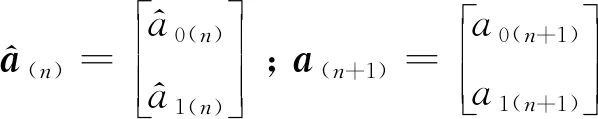
第n+1期新增沉降觀測數據為yn+1,相應權為pn+1,可建立觀測誤差方程為
(9)
將式(8)與式(9)聯立,得誤差方程式為
(10)
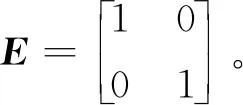
根據最小二乘法,可得當前預測模型系數的最優估值為
(11)
相應的權陣為
(12)
于是,高效更新后的沉降預測模型為
(13)
在上述方法中,歷史觀測數據對模型的影響已全部映射到預測模型的系數估值及其權陣中,利用序貫平差理論更新預測模型,已間接利用了歷史觀測數據。因此,該方法具有不需存儲歷史觀測數據,計算量小,更新出錯概率低等優點。
2.2 相關系數遞推算法
沉降預測模型的評價過程中,相關系數是個比較重要的指標[17-18],式( 5 )所示的傳統相關系數計算過程需要使用全部歷史數據,因此需推導與高效更新法相應的相關系數計算公式。

(14)
(15)
自m+1期起,即可利用遞推公式更新模型的相關系數,同樣以第n+1(n≥m)期數據為例,導出相關系數遞推公式。
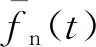
(16)
其中,離差平方和k1(n+1)可化為
(17)
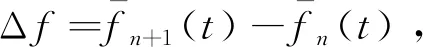
(18)
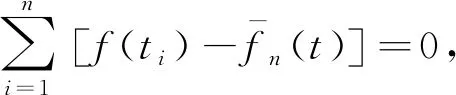
(19)
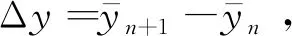
(20)
式(16)的分子可表示為
(21)
(22)
(23)
所以,綜合式(16)、式(20)~式(23)的結果,可得相關系數γn+1的遞推式為
(24)
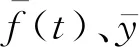
相關系數的遞推計算公式與高效更新方法保持了高度的一致,充分利用了遞推前的相關系數所包含的歷史數據信息,省略大量存儲、計算內容,降低了風險,提高了效率。
3 應用流程
以上內容介紹了模型高效更新方法的具體原理與詳細過程,為了更方便地對該方法進行利用,現將其應用流程總結為如下三個主要步驟:
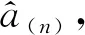
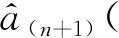
Step3計算更新后模型的相關系數γn+1(式(24))用以模型評價。
4 工程算例
4.1 工程背景
本文以橋梁沉降模型為例,對沉降預測模型的高效更新方法進行算例驗證。實驗數據選取滬蘇通長江公鐵大橋HTQ-1標段工程6#墩的實測沉降數據,從第4期開始構建沉降預測模型;實驗模型方法選用沉降預測模型中最常見的雙曲線模型,其模型表達式為
(25)
式中:S0、t0分別為架梁完工時的沉降量、觀測時間;α、β為根據實測值求出的系數;St、t分別為任意時間的沉降量、所對應的時間。
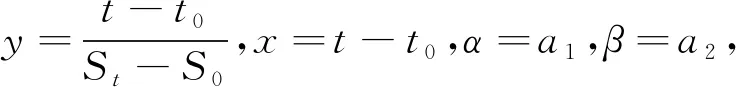
y=a0+a1x
(26)
根據模型的線性方程可以進行更新,更新完成后也可以得到模型的原表達式結果。
4.2 方法性能比較
選取全部觀測數據,用傳統更新方法隨時間更新沉降預測模型,更新結果見表1。
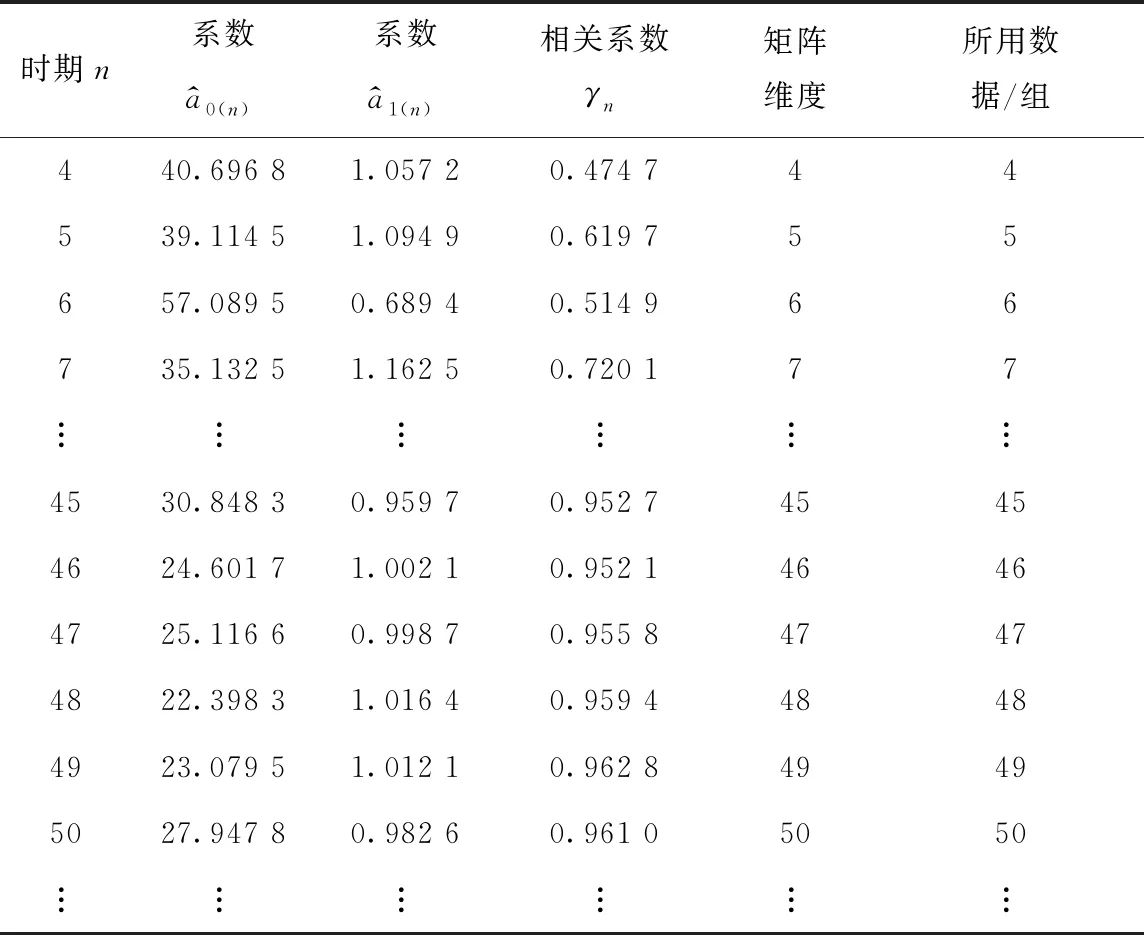
表1 傳統更新方法的更新結果
由表1可見,模型包含的數據量越多,其相關系數越趨近于1,表明其擬合效果越好。但與此同時,模型更新所需要的數據量與矩陣維度也快速增加,工程的計算量和計算復雜程度都會增加。
同樣的數據,按高效更新方法進行沉降預測模型的更新,更新結果見表2。
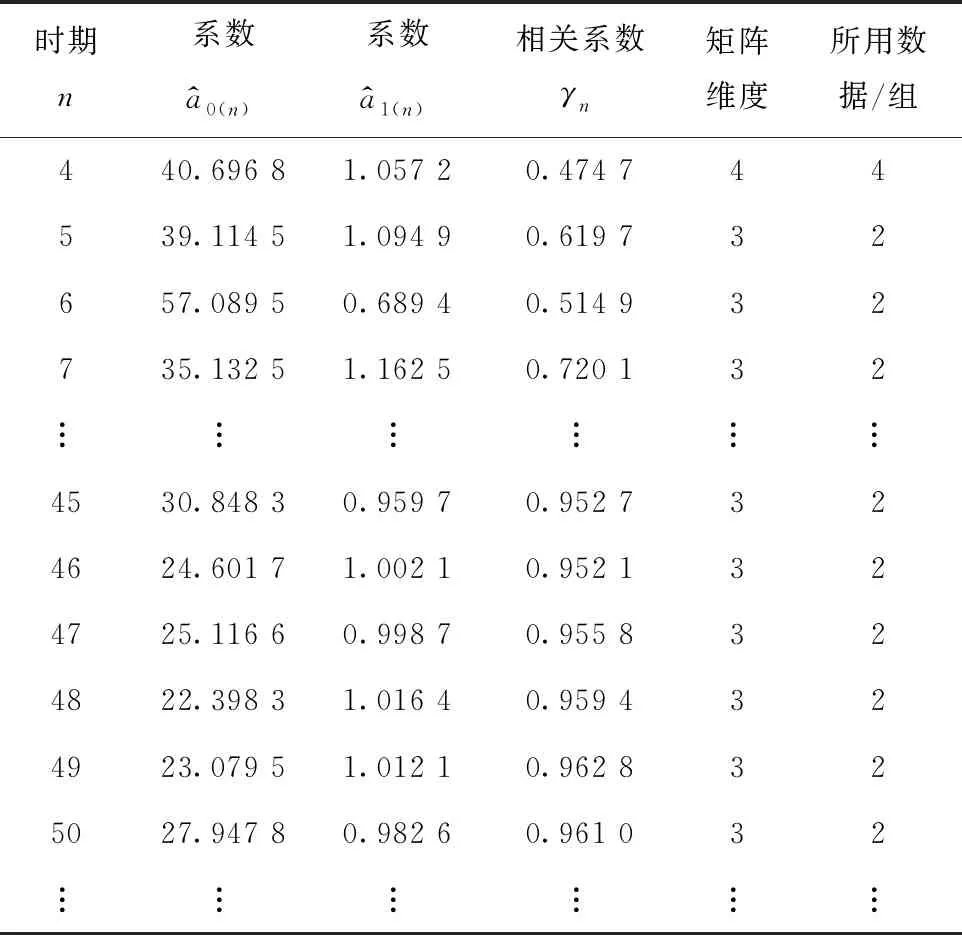
表2 高效更新方法的更新結果
由表2可見,高效更新方法與傳統更新方法得到的結果都完全一致,但在矩陣維度和所用數據方面,高效更新方法維度更小,使用數據更少。這表明在實際應用中,伴隨著工程進展,高效更新方法節約存儲、減少運算的優勢也會愈發凸顯。
5 結論
本文為解決傳統更新方法存儲量大、模型更新計算量大、存在數據誤用風險等問題,引入序貫平差的理論,對沉降預測模型的更新方法進行優化,得到了模型的高效更新方法,導出了相應的相關系數遞推公式,并利用實測數據對新方法進行了對比驗證。理論和算例均表明,本文新方法具有以下優點:
(1)避免了存儲歷史觀測值的麻煩。當前預測模型系數的先驗信息已包含了歷史觀測數據對模型影響的全部信息,因此不需存儲歷史觀測數據。
(2)提高了算法效率。高效更新方法只利用到了預測模型系數的相關信息,以及當前最新沉降觀測值信息,極大降低了計算過程中的矩陣維度,可顯著提高計算速度。
(3)提高了模型更新的可靠性。數據在存儲、拷貝、錄入過程中可能會存在丟失、被篡改、誤錄入的風險,新方法無需大量存儲、頻繁使用歷史數據,可杜絕此類風險,保證模型的正確更新。

