基于LASSO回歸的 R-vine copula 模型構(gòu)建及其在化工過(guò)程故障檢測(cè)中的應(yīng)用

鄧紅濤，賈 瓊，李紹軍，李 偉

(1.石河子大學(xué)，新疆 石河子 832000；2.華東理工大學(xué) 化工過(guò)程先進(jìn)控制和優(yōu)化技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室，上海 200237)

過(guò)程安全和產(chǎn)品質(zhì)量是目前化工過(guò)程被關(guān)注最多的兩個(gè)問題，而過(guò)程監(jiān)控是提高過(guò)程安全和產(chǎn)品質(zhì)量的重要手段。隨著集散控制和數(shù)據(jù)采集系統(tǒng)的廣泛應(yīng)用，工業(yè)過(guò)程采集數(shù)據(jù)的維度和數(shù)據(jù)量不斷增加，導(dǎo)致基于經(jīng)驗(yàn)知識(shí)和解析模型的方法在工業(yè)過(guò)程監(jiān)控領(lǐng)域的研究受到了限制[1]。基于數(shù)據(jù)驅(qū)動(dòng)的故障監(jiān)控建模方法通過(guò)統(tǒng)計(jì)與分析過(guò)程數(shù)據(jù)來(lái)挖掘系統(tǒng)的特性，在描述未知機(jī)理模型和缺乏過(guò)程知識(shí)的復(fù)雜過(guò)程問題研究中備受學(xué)術(shù)和工業(yè)界關(guān)注。傳統(tǒng)的數(shù)據(jù)分析方法有偏最小二乘法(PLS)[2]和主元分析法(PCA)[3]，這兩種方法適合分析具有線性、高斯分布特性數(shù)據(jù)。而處理非線性數(shù)據(jù)時(shí)常使用核方法來(lái)對(duì)這兩種方法進(jìn)行改進(jìn)，進(jìn)而形成核偏最小二乘(KPLS)法[4]、核主元分析(KPCA)法[5]等。這些方法主要是基于降維的方式將高維數(shù)據(jù)映射到低維特征空間，消除變量間的相關(guān)性，但在降維過(guò)程中數(shù)據(jù)攜帶信息量都會(huì)有一定的損失。

近年來(lái)，針對(duì)復(fù)雜數(shù)據(jù)的相關(guān)性研究中，copula理論得到了廣泛的應(yīng)用，將聯(lián)合概率分布函數(shù)與邊緣概率分布函數(shù)之間的相關(guān)性結(jié)構(gòu)建立聯(lián)系。由于多變量copula在構(gòu)建維數(shù)較大的數(shù)據(jù)間的依賴性時(shí)缺乏靈活性，Joe[6]提出了pair-copula，該方法是將多變量copula用一系列的二元copula來(lái)表示，該方法在刻畫高維數(shù)據(jù)的條件相關(guān)性、非對(duì)稱性、尾部相關(guān)性等方面均體現(xiàn)出更大的靈活性，已經(jīng)在金融、環(huán)境、工程等領(lǐng)域得到了廣泛的應(yīng)用。2015年Ren等[7]首先將vine copula函數(shù)引入到化工過(guò)程監(jiān)控領(lǐng)域，提出了基于vine copula 相關(guān)性描述的多模態(tài)故障檢測(cè)方法。Zheng等[8]利用D-vine copulas 混合模型實(shí)現(xiàn)了對(duì)復(fù)雜的工業(yè)過(guò)程監(jiān)控。周南等[9]利用核密度估計(jì)法構(gòu)建 R-vine copula 結(jié)構(gòu)并用在工業(yè)過(guò)程故障檢測(cè)中。由于二元copula函數(shù)類型眾多，vine copula結(jié)構(gòu)矩陣不固定，選取合適的vine copula結(jié)構(gòu)矩陣和copula函數(shù)類型成為建模的關(guān)鍵環(huán)節(jié)。目前常規(guī)方法是利用貪婪算法計(jì)算所有可能矩陣結(jié)構(gòu)下變量之間的相關(guān)關(guān)系，選擇相關(guān)性最大的矩陣結(jié)構(gòu)，然后根據(jù)赤池準(zhǔn)則(AIC)選取copula函數(shù)類型和參數(shù)[10-12]。這種方法在處理高維的工業(yè)過(guò)程數(shù)據(jù)時(shí)，會(huì)出現(xiàn)計(jì)算量大、計(jì)算時(shí)間長(zhǎng)的問題，其解也不能保證接近該高維組合優(yōu)化問題的最優(yōu)解。

筆者在構(gòu)建R-vine copula模型時(shí)引入LASSO回歸來(lái)統(tǒng)計(jì)變量之間的相關(guān)關(guān)系，根據(jù)變量間聯(lián)系的強(qiáng)弱程度確定變量在R-vine矩陣中的位置，利用回歸分析正則化路徑選擇R-vine copula矩陣結(jié)構(gòu)。遵循R-vine矩陣構(gòu)建規(guī)則和回歸過(guò)程中懲罰力度調(diào)整變量在矩陣中的位置，確定R-vine結(jié)構(gòu)矩陣模型，以獲得一個(gè)與變量獨(dú)立性有關(guān)的稀疏矩陣模型。該方法構(gòu)建的矩陣結(jié)構(gòu)獨(dú)立于copula函數(shù)類型和參數(shù)，在處理高維度復(fù)雜工業(yè)過(guò)程數(shù)據(jù)時(shí)，利用稀疏模型和懲罰力度簡(jiǎn)化copula函數(shù)類型選擇過(guò)程，縮短了建模時(shí)間，使統(tǒng)計(jì)建模具有更強(qiáng)的靈活性。該方法應(yīng)用在TE(Tennessee Eastman)過(guò)程中表現(xiàn)出較好的檢測(cè)效果。

1 R-vine copula 理論基礎(chǔ)和LASSO回歸

1959年Sklar第一次提出用copula函數(shù)分析復(fù)雜變量間的相關(guān)關(guān)系，將多維變量的聯(lián)合分布函數(shù)用邊緣分布函數(shù)和copula函數(shù)表示，但是這種copula函數(shù)面對(duì)高維數(shù)據(jù)時(shí)會(huì)出現(xiàn)參數(shù)過(guò)多而導(dǎo)致優(yōu)化困難的問題[11]。1996年Joe[6]提出了vine copula結(jié)構(gòu)。Vine copula結(jié)構(gòu)分解具有較大的靈活性，分解策略較多[13-14]。2002年Bedford等[15]定義了R-vine copula 結(jié)構(gòu)分解模型，相應(yīng)的多元分布結(jié)構(gòu)稱為R-vine結(jié)構(gòu)，可以更加靈活地表達(dá)變量之間的關(guān)系[16]。

1.1 構(gòu)建R-vine結(jié)構(gòu)矩陣規(guī)則

用樹結(jié)構(gòu)來(lái)表示vine結(jié)構(gòu)，對(duì)于n維變量的R-vine分布，包含了n-1棵樹，每棵樹由節(jié)點(diǎn)和邊組成。兩個(gè)節(jié)點(diǎn)確定一條邊，每條邊用二元copula函數(shù)表示。由于vine copula結(jié)構(gòu)分解模型多樣，樹型結(jié)構(gòu)不唯一。為了更好地表示vine copula的結(jié)構(gòu)，2013年Brechmann等[17]研究了一種R-vine copula結(jié)構(gòu)模型，利用一個(gè)下三角矩陣M來(lái)表示R-vine分解模型，用矩陣M可以簡(jiǎn)單地表示出R-vine 結(jié)構(gòu)中的樹集T、節(jié)點(diǎn)集V和邊集E。

對(duì)一個(gè)n維變量的vine copula結(jié)構(gòu)，可以用一個(gè)n×n的下三角矩陣M表示，矩陣對(duì)角線元素m代表變量X={x1,x2,…,xn}中的xm。用mi,j表示第i行第j列矩陣元素，mi,j∈{1,2,…,n}，i=(1,2,…,n)，j=(1,2,…,i)。矩陣元素之間需要滿足以下條件：

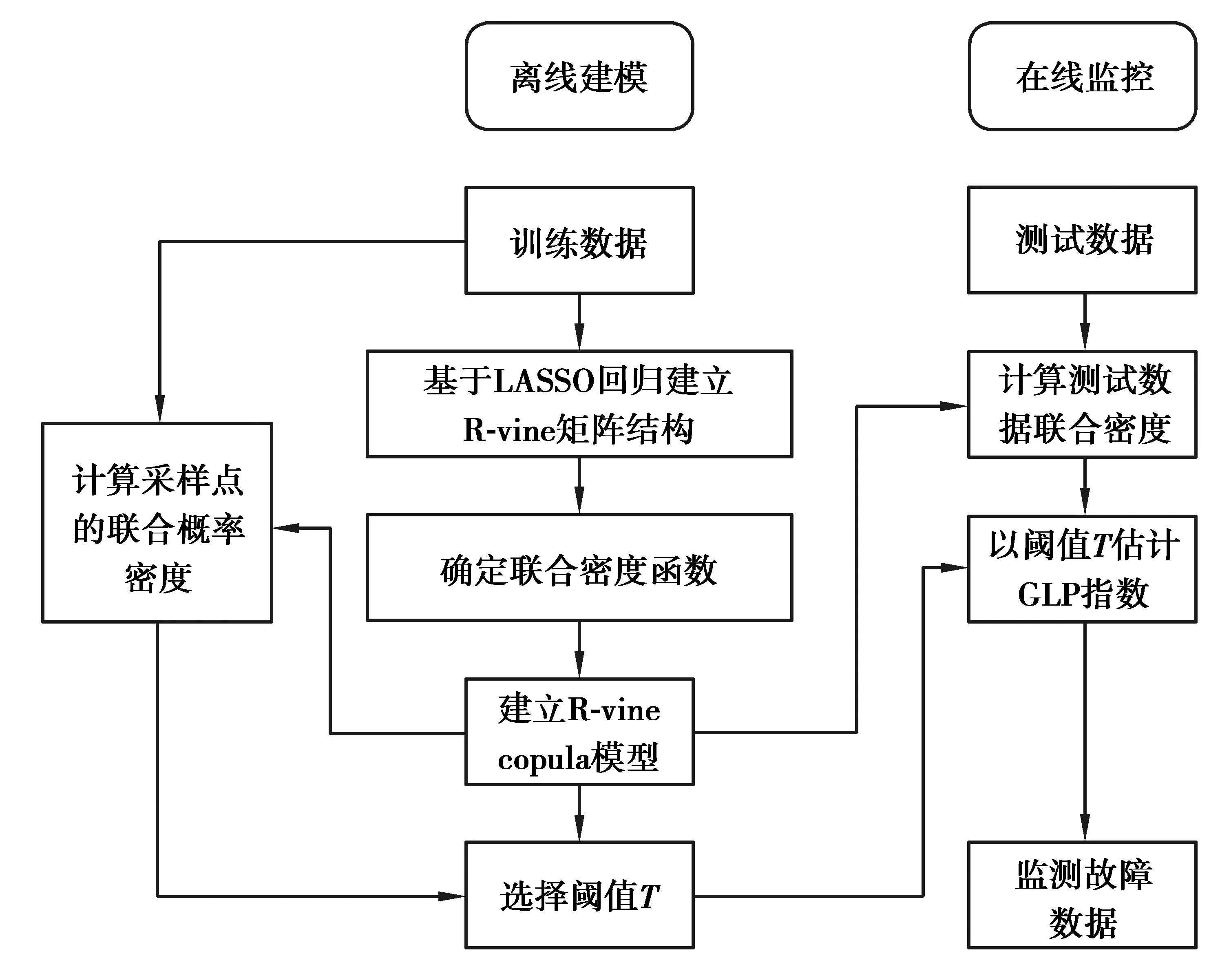
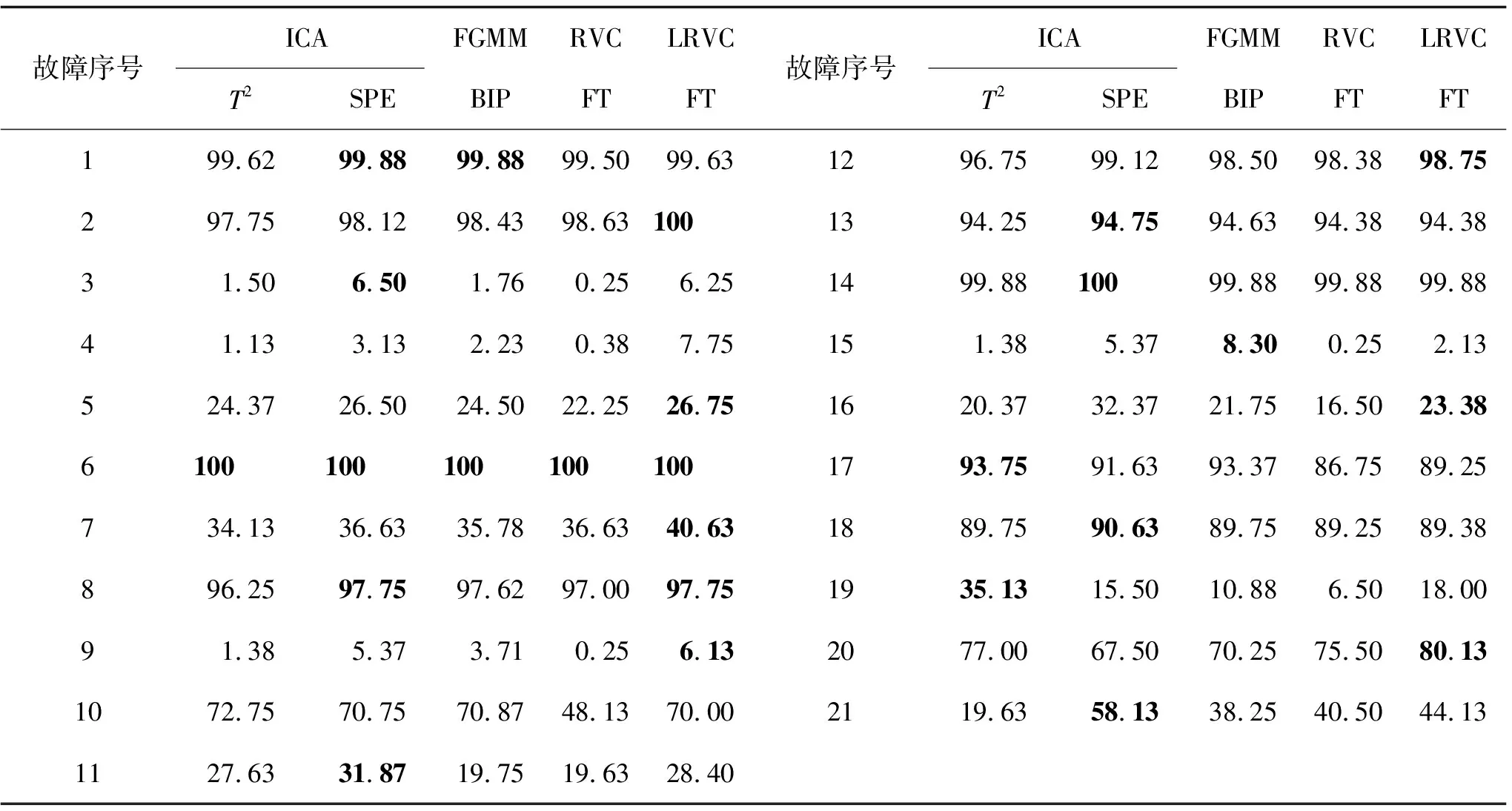
1){mj,j,…,mn,j}?{mi,i,…,mn,i}，1≤i

2)mj,j?{mi,i,…,mn,i}，1≤j

3){mi,j,{mi+1,j,…,mn,j}}?{mk,k,{mw,k,…,mn,k}}。即如果矩陣元素集Q={mi,j,{mi+1,j,…,mn,j}}，j=(1,2…,n-2)，i=(j+1,…,n)，那么一定存在包含或等于Q的元素集{mk,k,{mw,k,…,mn,k}}，j

設(shè)滿足以上規(guī)則的矩陣M中第i行第j列元素m集合為W。

根據(jù)以上條件可以發(fā)現(xiàn)矩陣中元素位置是互相約束的，如圖1所示矩陣M，組成第2列的變量{4,2,1,3}包含在第1列{5,2,1,3,4}中；第2列對(duì)角線元素{4}不會(huì)出現(xiàn)在第3、4、5列中；第1列畫圈元素組成元素集Q={3,4}，那么至少第2列中存在包含Q的元素集{4,1,3}。

圖1 5維變量的R-vine矩陣M

假設(shè)畫圈元素m4,1為O，O和第1列中行數(shù)大于4的元素組成元素集Q={O,4}。列數(shù)大于1、行數(shù)大于等于4的元素和對(duì)角線元素(帶上橫線元素)組成的元素個(gè)數(shù)大于等于Q的元素集{4,1,3}、{3,2,1}、{2,1}，這些元素集中包含元素4的只有{4,1,3}，根據(jù)條件3可知畫圈位置的元素O只能在變量集W={3,1}中選取。

1.2 利用矩陣M表示聯(lián)合密度函數(shù)

利用R-vine的矩陣結(jié)構(gòu)，不需要畫樹結(jié)構(gòu)就可以快捷地表示出多維變量的聯(lián)合密度函數(shù)[18]。矩陣元素mi,j和第j列元素可以表示樹Tn-i+1的第i-j+1個(gè)二元copula函數(shù)cj(e),k(e)|D(e)(Fj|D(xj(e)|xD(e)),Fk|D(xk(e)|xD(e)))，其中j(e)=mj,j，k(e)=mi,j，D(e)={mi+1,j,…,mn,j}，i=(2,3,…,n)，j=(1,2,…,i-1)，F(xiàn)為條件累計(jì)分布函數(shù)。

n維變量的聯(lián)合概率密度P可以表示為邊緣概率密度f(wàn)(xi)與copula密度函數(shù)c的乘積形式：

(1)

式中：fi(xi)為第i個(gè)變量xi的邊緣概率密度函數(shù)，cmj,j,mi,j|mi+1,j,…,mn,j為二元copula函數(shù)，F(xiàn)(xmj,j|xmi+1,j：mn，j)為xmj,j的條件累計(jì)分布函數(shù)。

圖1所示矩陣M為R-vine結(jié)構(gòu)矩陣，矩陣中元素m的值1-5代表變量X={X1,X2,X3,X4,X5}。矩陣M中畫圈元素m4,1=3，對(duì)應(yīng)二元copula為：c3,5|4，變量m1,1條件密度可以用第1列所有元素的二元copula函數(shù)之積和對(duì)角線元素的邊緣密度表示：

f(x5|x1x2x3x4)=f(x5)c4,5c3,5|4c1,5|3,4c2,5|1,3,4。

(2)

聯(lián)合概率密度為：

f(x1,x2,x3,x4,x5)=f(x1)f(x2|x1)×f(x3|x1x2)f(x4|x1x2x3)f(x5|x1x2x3x4)。

(3)

根據(jù)矩陣M求5維變量聯(lián)合概率密度，即：

f(x1,x2,x3,x4,x5)=f(x1)f(x2)f(x3)f(x4)f(x5)×c1,2c1,3c3,4c4,5c2,3|1c1,4|3c3,5|4c2,4|1,3c1,5|3,4c2,5|1,3,4。

(4)

在滿足矩陣規(guī)則的前提下構(gòu)造合理的R-vine結(jié)構(gòu)矩陣M是構(gòu)建R-vine copula模型的關(guān)鍵[19]。目前常用貪婪算法構(gòu)建R-vine樹的結(jié)構(gòu)矩陣，計(jì)算樹節(jié)點(diǎn)之間的相關(guān)性，按照最強(qiáng)相依性原則遍歷所有可能的矩陣結(jié)構(gòu)，尋找最大相關(guān)系數(shù)之和以構(gòu)建R-vine結(jié)構(gòu)矩陣，并在整個(gè)結(jié)構(gòu)選擇過(guò)程中迭代擬合copula函數(shù)及其參數(shù)。此方法計(jì)算時(shí)間長(zhǎng)，計(jì)算量大，構(gòu)建的模型結(jié)構(gòu)復(fù)雜，容易出現(xiàn)過(guò)擬合現(xiàn)象。

1.3 LASSO回歸

線性回歸表示變量間相互依賴的定量關(guān)系，變量x={x1,x2,…,xn}回歸函數(shù)如下：

(5)

式中φm為變量xm的回歸系數(shù)。

LASSO回歸是一種數(shù)據(jù)降維方法，善于處理變量的篩選。1996年Tibshirani[20]首次在普通線性回歸模型中添加了懲罰項(xiàng)，通過(guò)改變懲罰項(xiàng)將一些作用比較小的變量線性系數(shù)壓縮，最終變?yōu)榱悖瑥亩@得稀疏解。這種基于懲罰方法對(duì)樣本數(shù)據(jù)進(jìn)行變量選擇，防止了數(shù)據(jù)過(guò)擬合，不但可以用于線性關(guān)系，也可以用于非線性關(guān)系。回歸損失函數(shù)公式如下:

(6)

式中：hφ(x(t))是根據(jù)式(5)計(jì)算預(yù)測(cè)第t個(gè)樣本的值，因變量y為真實(shí)樣本值，q為樣本個(gè)數(shù)，t=(1,2,…,q)，λ為正則化參數(shù)，r為參數(shù)個(gè)數(shù)，k=(1,2,…,r)。隨著λ增大，各變量的系數(shù)逐漸趨于零。

2 利用LASSO回歸構(gòu)建R-vine矩陣

將LASSO回歸算法用于構(gòu)建R-vine結(jié)構(gòu)矩陣，提出一種新的構(gòu)建R-vine結(jié)構(gòu)矩陣的方法[21]。如構(gòu)建n維變量X={X1,X2,…,Xn}的R-vine結(jié)構(gòu)矩陣M。

首先確定R-vine結(jié)構(gòu)矩陣M中的對(duì)角線元素。將變量帶入式(7)，按照式(6)利用交叉驗(yàn)證方法確定過(guò)程變量xi(i=1,2,…,n)的LASSO回歸方程。

(7)

式中：m=1,2,…,n，z=1,2,…,n，且m≠z。根據(jù)式(8)統(tǒng)計(jì)n個(gè)回歸方程中變量xm的回歸系數(shù)φm,z非零的個(gè)數(shù)uz，按照uz的升序?qū)⒆兞縳m設(shè)為R-vine結(jié)構(gòu)矩陣M的對(duì)角線元素，當(dāng)出現(xiàn)次數(shù)相同時(shí)按照回歸系數(shù)的和排序。

(8)

如圖1所示，矩陣M確定對(duì)角線元素時(shí)，存在u5≤u4≤u3≤u2≤u1，那么對(duì)角線元素為{5,4,3,2,1}。

接下來(lái)按照從右往左、從下至上的順序確定矩陣中的其他元素。如確定矩陣M中的變量mi,j，以矩陣對(duì)角線元素xmj,j為因變量y，根據(jù)R-vine結(jié)構(gòu)矩陣構(gòu)建規(guī)則，以滿足元素集W的元素為自變量，帶入式(5)，根據(jù)式(9)利用最小回歸角方法選擇變量，當(dāng)回歸系數(shù)依次置為零時(shí)，懲罰項(xiàng)最大的變量即為mi,j。

(9)

式中：W為根據(jù)R-vine矩陣規(guī)則確定的此處可放置的變量集合，l是屬于集合W的元素。

確定圖1中矩陣M第5行第4列的元素，根據(jù)R-vine矩陣規(guī)則可知m5,4=1，然后按照從右往左、從下至上的順序依次確定m5,3、m5,2、m5,1、m4,3、m4,2、m4,1、m3,2、m3,1、m2,1。確定畫圈元素m4,1時(shí)，根據(jù)構(gòu)建R-vine結(jié)構(gòu)矩陣規(guī)則推出可用變量W={1,3}，則以m1,1為自變量y，以m4,2和m5,5為因變量，按照式(5)利用LASSO回歸計(jì)算回歸系數(shù)，按照式(9)利用最小回歸角方法調(diào)整懲罰項(xiàng)。當(dāng)φ1=0時(shí)λ=λ1；φ3=0時(shí)λ=λ3。因?yàn)榇嬖讦?<λ3，那么m4,1=3。

3 基于LASSO構(gòu)建R-vine copula模型的故障檢測(cè)方法

本研究中利用LASSO回歸過(guò)程反映變量之間關(guān)系的特點(diǎn)，按照變量回歸系數(shù)歸零速度和懲罰項(xiàng)大小確定R-vine結(jié)構(gòu)矩陣M，利用正常樣本數(shù)據(jù)根據(jù)赤池準(zhǔn)則確定R-vine copula模型中參數(shù)，構(gòu)建模型，利用閾值法進(jìn)行在線故障檢測(cè)(如圖2所示)。

圖2 LRVC過(guò)程監(jiān)控方法示意圖

3.1 離線建模

1)獲得正常操作過(guò)程的訓(xùn)練樣本集，按照第2節(jié)方法構(gòu)建R-vine矩陣M。

2)根據(jù)R-vine矩陣M確定copula對(duì)和參數(shù)，構(gòu)建R-vine copula模型。合適的copula對(duì)能夠精確地描述變量數(shù)據(jù)間的相關(guān)關(guān)系。采用基于似然函數(shù)的赤池信息準(zhǔn)則[23]選取最合適copula對(duì)類型。赤池準(zhǔn)則是權(quán)衡被估計(jì)模型復(fù)雜度和擬合優(yōu)越性的一種標(biāo)準(zhǔn)，其定義如下：

(10)

3)確定檢測(cè)閾值T。

計(jì)算樣本點(diǎn)的聯(lián)合概率密度，利用分位數(shù)法[7]求對(duì)應(yīng)的聯(lián)合概率密度中閾值T。該方法根據(jù)高密度區(qū)域與密度分位數(shù)理論構(gòu)建廣義貝葉斯推斷概率指標(biāo)(GLP)，閾值T選取99%的控制限，監(jiān)測(cè)時(shí)對(duì)比靜態(tài)密度分位數(shù)表確定監(jiān)測(cè)狀態(tài)。

3.2 在線監(jiān)控

1)利用模型計(jì)算監(jiān)測(cè)數(shù)據(jù)聯(lián)合概率密度函數(shù)。

2)以閾值T為界限，小于閾值則為故障數(shù)據(jù)。

4 應(yīng)用分析

4.1 TE過(guò)程

Eastman 公司依照實(shí)際的化工反應(yīng)過(guò)程開發(fā)了TE測(cè)試平臺(tái)，仿真數(shù)據(jù)具有非線性、時(shí)變和強(qiáng)耦合性等特征，能很好地模擬復(fù)雜工業(yè)過(guò)程，被廣泛應(yīng)用于控制、優(yōu)化、過(guò)程監(jiān)控與故障診斷的研究。TE數(shù)據(jù)集由訓(xùn)練集和測(cè)試集構(gòu)成，數(shù)據(jù)集包含了正常狀態(tài)數(shù)據(jù)和21種故障狀態(tài)數(shù)據(jù)，每個(gè)樣本都有52個(gè)觀測(cè)變量，其中連續(xù)變量22個(gè)，操縱變量12個(gè)和成分變量19個(gè)。本研究所用數(shù)據(jù)可從http:∥web.mit.edu/braatzgroup/links.html下載，在離線狀態(tài)下選取了正常工況下樣本52個(gè)變量中的22個(gè)連續(xù)的過(guò)程變量構(gòu)建R-vine copula模型，采用960個(gè)正常樣本點(diǎn)來(lái)建立模型，每種故障狀態(tài)的測(cè)試數(shù)據(jù)也選用960個(gè)樣本點(diǎn)進(jìn)行測(cè)試，對(duì)21個(gè)故障數(shù)據(jù)進(jìn)行監(jiān)測(cè)。將本研究中提出的方法LRVC與獨(dú)立成分分析(ICA)、高斯混合模型(FGMM)、R-vine copula(RVC)等算法計(jì)算TE過(guò)程故障檢測(cè)率進(jìn)行比較，結(jié)果見表1,其中T2和SPE是ICA故障檢測(cè)的統(tǒng)計(jì)指標(biāo)，T2指標(biāo)衡量樣本向量在主元空間的變化，SPE指標(biāo)衡量樣本向量在殘差空間的投影的變化，BIP是貝葉斯推理的后驗(yàn)概率(BIP)指標(biāo)，F(xiàn)T指利用RVC模型和LRVC模型下的廣義貝葉斯推斷概率指標(biāo)。表中粗體表示檢測(cè)效果最好的值。

表1 TE過(guò)程故障檢測(cè)率對(duì)比表

可以看出利用LASSO回歸構(gòu)建的R-vine模型監(jiān)測(cè)結(jié)果優(yōu)于貪婪算法構(gòu)建R-vine矩陣建模，與FGMM、ICA方法[23-24]比較具有較高的檢測(cè)率。LRVC模型的故障檢測(cè)率都略高于利用貪婪算法構(gòu)建矩陣的模型檢測(cè)率，在故障2、4～9、12、16、20中都表現(xiàn)出較好的檢測(cè)效果，其他故障的檢測(cè)效果和其他方法相差不多。LRVC模型有13類故障的檢測(cè)率都高于FGMM方法的檢測(cè)結(jié)果，相比于ICA檢測(cè)方法在故障2、4、5、7、9、12、20中都表現(xiàn)較好檢測(cè)率。

TE過(guò)程中數(shù)據(jù)具有非高斯態(tài)的特性，F(xiàn)GMM方法是基于馬氏距離判斷數(shù)據(jù)是否異常，反映數(shù)據(jù)的非高斯特性能力較差；ICA方法在數(shù)據(jù)變換和特征提取的過(guò)程中會(huì)造成部分信息的損失。而LRVC方法利用LASSO回歸建立R-vine矩陣構(gòu)建模型，全面挖掘出數(shù)據(jù)變量之間的信息，在刻畫非高斯、非線性方面有顯著的優(yōu)勢(shì)，提高了故障檢測(cè)的性能。圖3為L(zhǎng)RVC方法對(duì)故障8和故障12的監(jiān)控圖，橫坐標(biāo)為對(duì)聯(lián)合概率密度P取對(duì)數(shù)。

圖3 TE過(guò)程故障 8、12的LRVC監(jiān)控圖

4.2 醋酸脫水過(guò)程

醋酸脫水過(guò)程控制系統(tǒng)包括4個(gè)進(jìn)料和90級(jí)塔板，用于建模的300組測(cè)試數(shù)據(jù)和500組訓(xùn)練數(shù)據(jù)來(lái)自分布式控制系統(tǒng)(DCS)，包括溫度、流量、壓力等連續(xù)的21個(gè)監(jiān)測(cè)變量。表2為核主元分析KPCA、FGMM、和LRVC 3種方法的檢測(cè)率(fault detection rate，F(xiàn)DR)和誤報(bào)率(false positive rate，F(xiàn)PR)，可見LRVC方法在醋酸脫水過(guò)程監(jiān)測(cè)中表現(xiàn)較好。

表2 醋酸脫水過(guò)程檢測(cè)率和誤報(bào)率

5 結(jié) 論

提出了一種基于LASSO回歸構(gòu)建 R-vine copula 模型的化工過(guò)程故障檢測(cè)方法LRVC，與傳統(tǒng)方法相比具有較好的檢測(cè)效果。LRVC模型利用LASSO回歸過(guò)程反映變量之間相關(guān)性的特性，依據(jù)回歸過(guò)程懲罰力度構(gòu)建R-vine矩陣，采用赤池準(zhǔn)則進(jìn)行copula類型選擇構(gòu)建R-vine copula模型。模型中利用LASSO回歸統(tǒng)計(jì)多元變量相關(guān)性構(gòu)建R-vine矩陣更能體現(xiàn)vine copula結(jié)構(gòu)分解特性，適合高維變量數(shù)據(jù)分析。基于LRVC模型的過(guò)程故障檢測(cè)方法充分利用了copula函數(shù)可以反映變量之間非高斯、非線性的特性，在不降維的情況下直接描述變量之間關(guān)系，具有更好的解釋能力和適應(yīng)性。此方法簡(jiǎn)化了構(gòu)建R-vine矩陣過(guò)程，在超高維變量的建模過(guò)程中可以直接利用矩陣進(jìn)行copula函數(shù)的選擇，節(jié)省了建模時(shí)間。該方法在TE過(guò)程以及醋酸脫水過(guò)程中的應(yīng)用表明其在工業(yè)過(guò)程故障檢測(cè)中具有應(yīng)用前景。