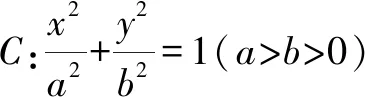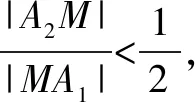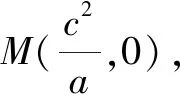重方法,求效益:活用函數與方程思想
過家福
江蘇省南菁高級中學
作為中學數學中最基本的思想之一——函數與方程思想,在歷年高考數學題中都占有比較大的比重,各種難易程度、各類題型都可能涉及.利用函數的概念、性質、運算、圖象等來分析、轉化與解決問題就是函數思想;利用數量關系,通過方程、不等式及其二者的交匯等數學模型的構建來分析、處理與解決問題就是方程思想.利用函數與方程思想,重在提煉技巧方法,提升解題效益.
1 在不等式中的應用
不等式與函數、方程之間構建特殊的一一對應關系,利用這個特殊關系,經常可以將不等式問題轉化為相應的函數(或方程)來處理,借助函數的圖象與性質,或方程的解或零點等知識加以巧妙轉化,很好用來處理涉及代數式的大小關系、不等式恒成立以及抽象不等式等相關問題.
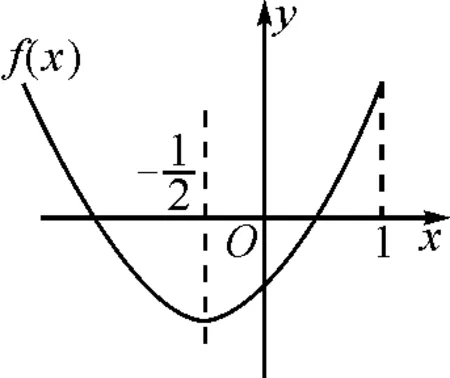
例1已知實數a滿足0 A.ea-1 C.ae 分析:根據題目條件,通過構建函數f(x)=ex-x-1(x>0),利用導數研究函數的單調性,進而確定ea-1與a的大小關系;再利用指數函數的單調性進一步確定a與ae的大小關系即可. 解析:設函數f(x)=ex-x-1,x>0,求導則有f′(x)=ex-1>0,所以函數f(x)在(0,+∞)上是增函數,且f(0)=0. 于是f(x)>0,所以ex-1>x,即ea-1>a. 又指數函數y=ax(0 故選擇答案:B. 點評:在解決一些相關的不等式問題中,經常借助不等式之間的結構特征等形式,利用不等式與函數或方程之間特殊的對應關系,合理構建相應的函數或方程,進而借助函數或方程的求解與應用來解決相應的不等式問題. 數列是一類特殊的函數模型,是涉及項數n所對應的正整數的函數模型,特別是相關數列的通項公式與前n項和公式等函數類問題,可以根據題目條件轉化為對應的函數或方程來處理,解決一些涉及最值或取值范圍的應用問題,注意其中項數n必須是正整數這一特殊限制條件. 分析:根據題目條件,結合等比數列的定義確定對應的公比,通過等比數列的前n項和公式確定Sn的表達式,利用參數n是奇數與偶數的不同情況進行分類討論,從而確定函數Sn的單調性及取值范圍,進而求解對應數列關系式的值. 點評:數列是一類定義域為正整數集或其有限子集的特殊函數,回歸本質,借助函數或方程的知識來解決數列中的相關問題,是破解數列應用問題比較常見的一種思維方式.只是解題過程中要注意數列問題中項數n的取值為正整數,涉及的函數或方程具有離散性特點. 三角函數中有關三角方程根的計算問題、含參的三角函數或三角方程的求參問題等,經常轉化為函數關系,利用相應函數的圖象與性質求解,或轉化為方程問題,利用方程有解的情況來分析與處理. 分析:根據題目條件,可以將對應的含參三角方程分離參數,結合函數的構建,利用限制條件下的二次函數的值域求解來確定實數a的取值范圍;也可以進行換元處理,化方程問題為對應的函數問題,利用方程在給定區間上有根的條件構建不等式(組)來處理. 解法1:把方程cos2x-sinx+a=0變形為a=-cos2x+sinx. 所以a的取值范圍是(-1,1]. 故填答案:(-1,1]. 依題意則知二次方程t2+t-1-a=0在t∈(0,1]上有實數解. 圖1 解得-1 故填答案:(-1,1]. 點評:在解決一些含參的三角函數問題中,經常可以利用整體化思維或換元思維,將三角函數問題轉化為對應的二次函數或二次方程問題,巧妙利用二次函數的圖象與性質、二次方程根的分布情況等來數形結合,直觀形象地解決相應的三角函數的應用問題,實現問題的合理轉化與巧妙破解. 有關平面向量中的模或夾角的計算問題、參數的求值或取值范圍問題等,經常結合平面向量的數量積公式,或利用坐標法等,化歸轉化為對應的函數關系,借助相關函數的圖象與性質來分析與求解. 分析:根據題目條件,通過對所求平面向量的模進行平方處理,結合數量積公式加以展開,轉化為關于x的二次函數問題,利用二次函數的圖象與性質來確定相應的最值問題即可. 點評:有關平面向量模的問題,通常利用平方法處理,將平面向量問題轉化為對應的平面向量的數量積問題,從而構建函數或方程模型,利用函數與方程的思想來合理轉化與巧妙破解.在解決一些最值或取值范圍問題中經常用到此思想方法. 涉及解析幾何中有關直線與圓錐曲線位置關系的問題,經常借助聯立方程組,轉化為對應的方程問題,利用相關的求值合理構建相應的函數等.例如,解決一些涉及長度、角度、代數式等要素的最值、取值范圍等相關問題,以及定點、定值的判斷與證明等問題時,經常離不開函數與方程思想. 故選擇答案:C. 點評:解決解析幾何中范圍問題的關鍵是通過直線、曲線等相關方程的轉化,構建對應的函數或方程關系,借助函數的基本性質、方程有解的條件等構建相關關系式,進而求解最值、取值范圍、定點、定值等相關解析幾何問題. 事實上,函數與方程思想在其他相關知識中的用處也是非常大,主要是根據題意,構造恰當的函數,利用函數基本性質或函數圖象加以解決;或建立相應的方程,利用方程的解、方程有根的條件的推理分析等.從不同層面加以化歸轉化,化難為易,化生為熟、化繁為簡,從而解決一些相關的綜合與應用問題.Z2 在數列中的應用
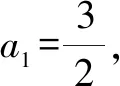
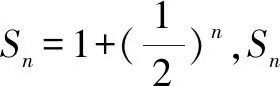
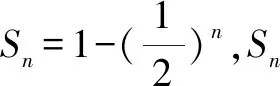
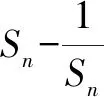
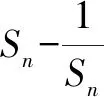
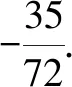
3 在三角函數中的應用
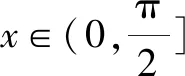
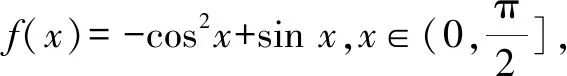
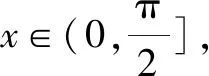
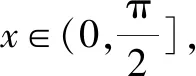
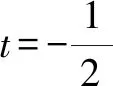
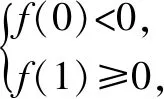
4 在平面向量中的應用
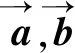
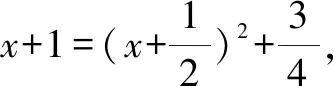
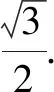
5 在解析幾何中的應用