雙饋風機等效慣量控制比例系數對系統功角首擺穩定的影響機理分析

王 科 秦文萍 張 宇 朱志龍 薛邵鍇

雙饋風機等效慣量控制比例系數對系統功角首擺穩定的影響機理分析

王 科 秦文萍 張 宇 朱志龍 薛邵鍇

（電力系統運行與控制山西省重點實驗室（太原理工大學） 太原 030024）

隨著具備慣量調節能力的雙饋風力發電機組大規模接入電網，電網的功角穩定特性變得更加復雜。該文以雙饋風機（DFIG）接入兩區域互聯電網為研究背景，首先推導兩區域慣性中心等效模型，分析DFIG直接接入電網時虛擬慣量對兩區域慣性中心轉子運動方程的影響；然后從系統暫態能量的角度出發，研究系統發生三相短路故障及負荷突增時，系統功角擺動方向不同、兩區域互聯系統DFIG等效慣量控制環節比例系數不同對系統加速及減速過程中暫態能量的影響，進而研究其對系統功角首擺穩定的影響機理；最后通過系統功角首擺最大偏移量對系統功角首擺穩定性進行評估，并在PSASP仿真軟件中搭建兩區域系統仿真模型，驗證所提理論的正確性。

雙饋風機 等效慣量控制比例系數 暫態能量函數 系統功角首擺穩定

0 引言

與傳統同步機相比，雙饋風力發電機（Doubly-Fed Induction Generator, DFIG）缺乏慣性響應能力[1-2]，因此，大規模雙饋風機接入后的電力系統遭受大擾動或小擾動時（三相短路、負荷突增等），系統慣性響應能力缺失嚴重，暫態功角穩定問題突顯。隨著雙饋風機虛擬慣量控制技術不斷完善，雙饋風機能夠為系統提供動態慣性支撐[3-5]，因此，亟須開展雙饋風機虛擬慣量對系統功角首擺穩定影響機理的研究。

當前，國內外學者研究雙饋風機慣量控制比例系數對系統功角穩定性的影響時，主要考慮送/受端區域內DFIG分別附加虛擬慣量控制[6-10]，但對送受端區域內DFIG同時附加慣量控制缺乏考慮，較少關注兩區域互聯系統DFIG虛擬慣量控制環節比例系數對系統功角穩定的影響機理。文獻[7]對送端/受端分別附加虛擬慣性對系統暫態穩定的影響進行研究，提出系統受到擾動后，若功角首擺為正、增加受電區域內風電機組的虛擬慣量時，系統功角穩定性降低；增加送電區域內風電機組的虛擬慣量時，系統暫態穩定水平取決于減速能量的減小幅度。功角反向擺動時，風電場虛擬慣量的控制效果與功角正擺時相反。文獻[8]研究送端/受端區域內DFIG接入對系統相對轉速加速度的偏差函數的影響，提出兩區域間相對轉速加速度的變化趨勢主要由并網DFIG和新增負荷的暫態功率響應的差值決定，也受到系統故障期間并網DFIG與新增負荷端電壓跌落幅度的影響。文獻[9]研究兩機系統中送/受端系統慣性時間常數變化對系統功角暫態穩定性的影響，提出當送端機組出力小于受端機組出力，且兩端機組出力相差較大時，受端系統慣性時間常數增大，系統暫態穩定水平提高；當兩端機組出力相差不大，或送端機組出力大于受端機組出力時，受端系統慣性時間常數增大，系統暫態穩定水平下降。在兩機系統中，相同的運行方式下，受端系統慣性時間常數增大和送端系統慣性時間常數增大對電網暫態穩定水平的影響大致相反。文獻[10]研究不同運行方式、不同故障位置、火電與風電不同配比條件對高滲透率風電的送端電網系統暫態穩定性的影響。

有學者提出“區域慣性中心等效理論”分析互聯系統功角首擺穩定的內在機理，將系統中具有緊密電氣聯系和相似的暫態功角行為特征的同步發電機組劃分為同一區域。通過推導各區域慣性中心轉子運動方程，研究區域互聯系統功角首擺穩定的內在機理[11]，在多機系統的暫態穩定分析中具有重要意義。薛禹勝院士提出從暫態能量的角度分析系統遭受大干擾和小干擾后功角首擺穩定內在機理[12]。文獻[13]基于DFIG的大容量風電機組接入單機無窮大系統模型，推導出含風機的網絡暫態能量函數，分析含有大容量風電的系統暫態穩定性。文獻[14-16]將兩區域互聯系統等值為單機無窮大系統模型，進而分析大規模風電接入后系統功角暫態穩定性。

現有文獻大多基于擴展等面積定則推導系統極限切除角和極限切除時間，進而分析系統功角穩定內在機理，較少關注在第一個振蕩周期內系統功角變化規律及內在機理。文獻[17-20]將含DFIG的兩機系統等值為含DFIG的單機無窮大系統，運用等面積法則分析風機接入位置、容量等對系統極限切除角、極限切除時間進行理論計算，而未關注系統功角首擺穩定的內在機理。

因此，本文以DFIG接入兩區域電網為研究背景，首先建立兩區域慣性中心等效模型，分析DFIG虛擬慣量對兩區域慣性中心同步機轉子運動方程的影響；然后從暫態能量函數的角度出發，分析系統發生三相短路故障及負荷突增時，系統功角擺動方向不同、兩區域互聯系統DFIG等效慣量控制比例系數不同，對系統加速及減速過程中暫態能量的影響，進而研究對系統功角首擺穩定性的影響機理；最后提出系統功角首擺最大偏移對系統功角穩定性進行評估，并在PSASP中搭建兩區域互聯系統仿真模型對上述理論進行仿真驗證。

1 DFIG等效慣性時間常數

1.1 DFIG等效慣性時間常數定義

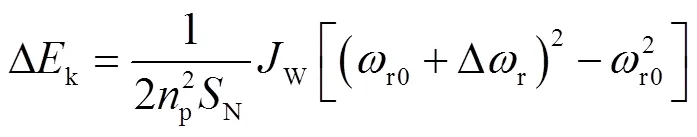
式中，p為DFIG定子繞組極對數；N為額定容量；W為固有轉動慣量；r0為初始轉子角速度；Δr為轉子角速度增量。

DFIG經典虛擬慣量控制模型如圖1所示，由于慣性響應過程中DFIG轉速與系統角速度耦合，DFIG動能變化量可表示[21]為

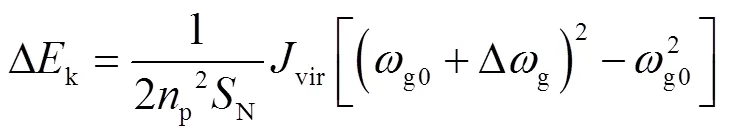
式中，Jvir為DFIG等效轉動慣量；ωg0為系統初始同步角速度；Δωg為系統同步角速度增量。

由式（1）和式（2）可知，DFIG等效轉動慣量可表示為

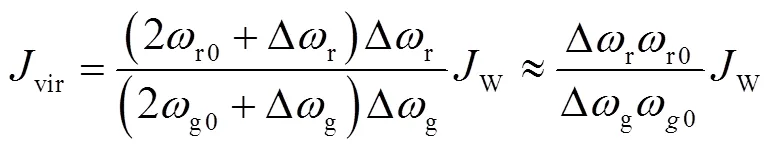
DFIG等效慣性時間常數定義為額定轉速下存儲的動能與額定容量的比值[21]，即

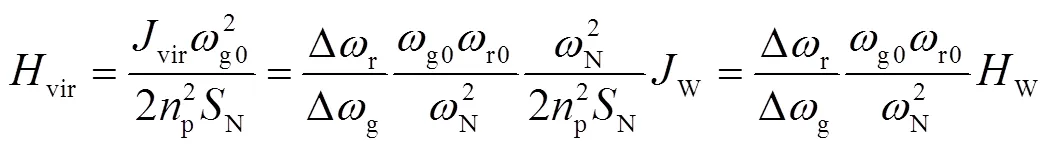
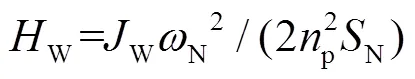
1.2 DFIG等效慣性時間常數頻域表達式

DFIG虛擬慣量響應過程中，由于電流內環響應速度遠大于發電機機電暫態過程，因此將電流內環等效為一階慣性環節。定子磁鏈的變化忽略不計[22]，近似認為保持不變，DFIG電磁功率參考值變化量Δref由最大功率跟蹤控制提供的Δopt和慣量控制提供的Δvir決定，即

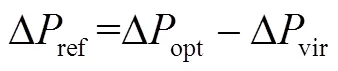
假設DFIG轉速從r0變化到r1，轉速變化較小，Δopt、Δvir可表示為[22]

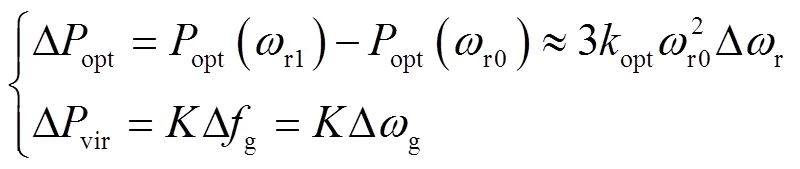
式中，opt為最大功率跟蹤曲線的比例系數；為慣量控制比例系數。

Δref、Δe可表示為

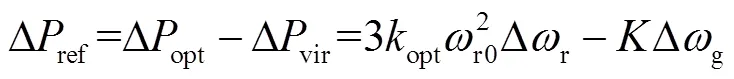
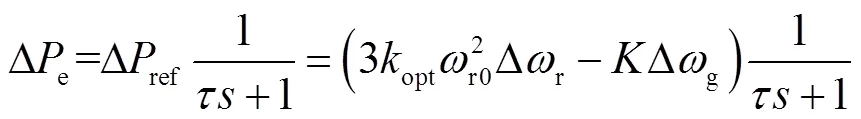
式中，為變流器時間常數，取0.02s。

當DFIG轉速變化時，DFIG轉子運動方程為

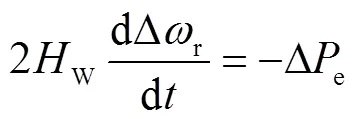
將式（8）代入式（9）可得

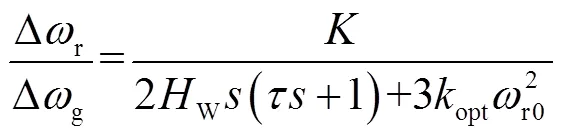
將式（10）代入式（4）可得DFIG等效慣性時間常數頻域表達式為

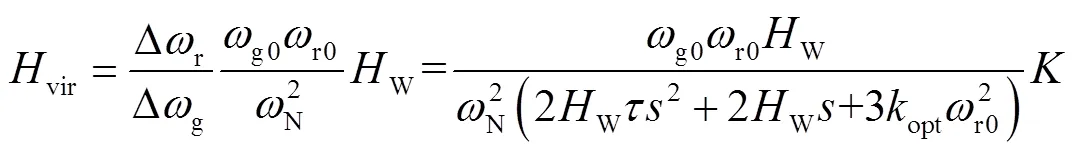
若令

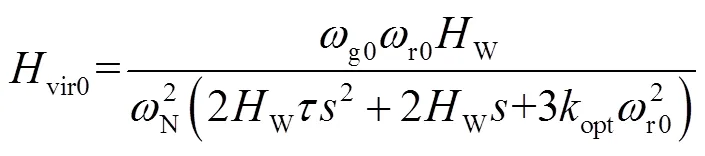
vir可進一步表示為

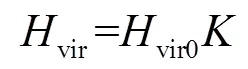
式中，vir0表征慣量響應過程中DFIG等效慣性時間常數vir變化趨勢；表征DFIG等效慣性時間常數vir大小。

由式（13）可知，若風電場內DFIG具有相同基本參數，DFIG慣量響應過程中等效慣性時間常數vir0在時域內具有相同的變化趨勢，首先迅速達到最大值，隨后開始下降，最終趨于穩定[22]。

2 兩區域慣性中心等效模型

假設遭受大擾動或小擾動后系統的失穩模式為兩機模式，根據聯絡線功率傳輸方向將系統兩側同步機分為送端機群及受端機群，G1為送端機群（S機群），G2為受端機群（R機群）[23]，DFIG直接接入送受端機群的并網母線，兩機系統等效模型如圖2所示。

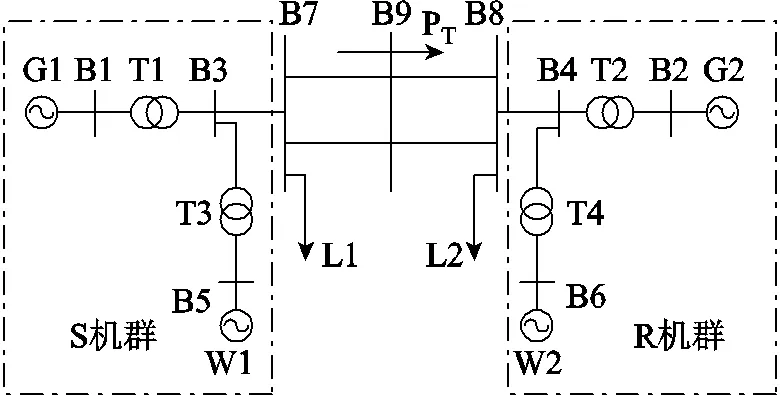
圖2 兩區域互聯系統等效模型

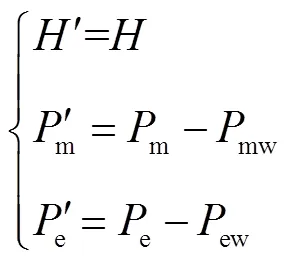
由DFIG轉子運動方程可知，DFIG機械功率及電磁功率可表示為

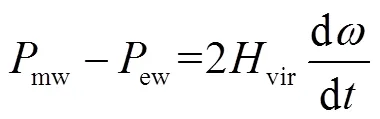
式中，為DFIG所在區域內同步發電機轉速。

假設S機群同步機功角超前于R機群，系統兩側同步機轉子運動方程表達式修正為[24]

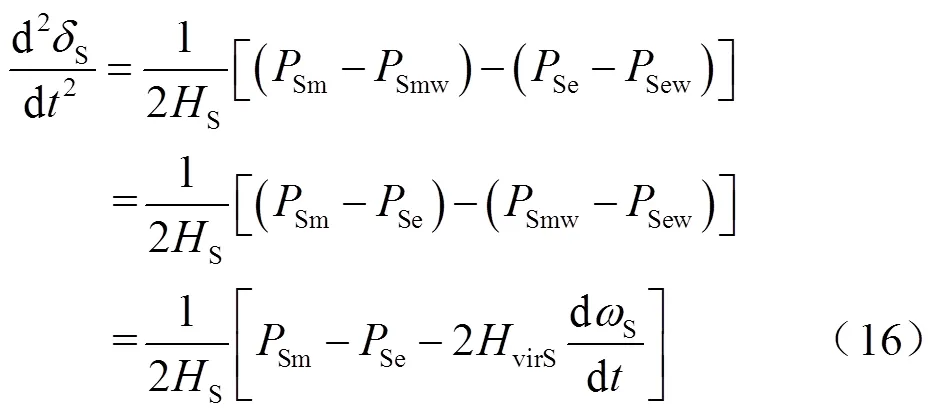
式中，S、R分別為S機群、R機群等效功角；SR為系統功角，SR=S-R；Sm、Rm、Se、Re分別為DFIG接入前S機群、R機群同步機等值機械功率和電磁功率；Smw、Rmw、Sew、Rew分別為S機群、R機群內DFIG的機械功率和電磁功率；S、R分別為S機群、R機群同步機慣性時間常數；virS、virR分別為S機群、R機群DFIG等效慣性時間常數；S、R分別為S機群、R機群同步機轉速；DW為DFIG接入引起的系統等值功率變化量。

3 擾動后系統暫態能量函數分析

3.1 功角正向擺動

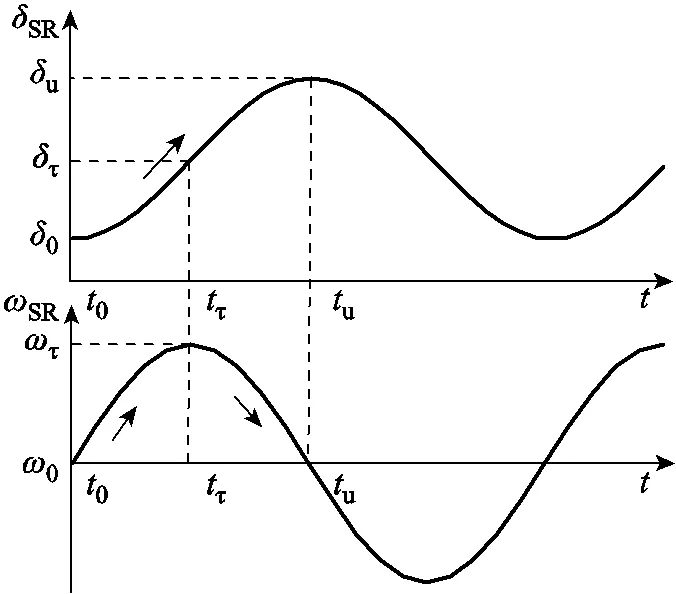
圖3 系統功角正向擺動

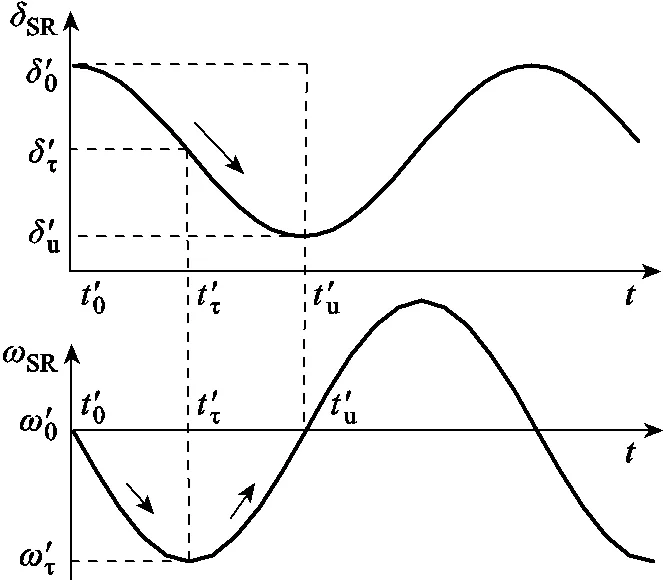
圖4 系統功角反向擺動

功角正向擺動時，系統暫態能量T可表示為

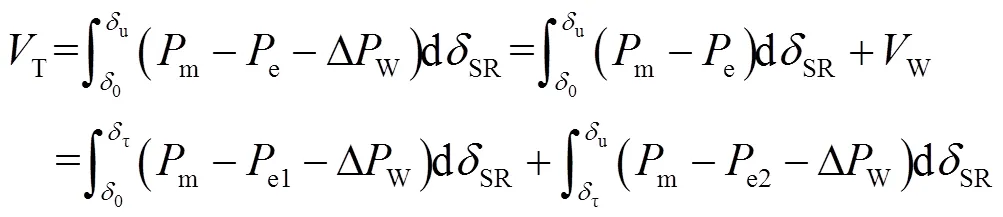
式中，e1、e2分別為系統加速及減速期間等值電磁功率；W為DFIG提供的暫態能量，可表示為

式中，Winc和Wdec分別為系統加速及減速過程中DFIG提供的暫態能量。

3.2 功角反向擺動

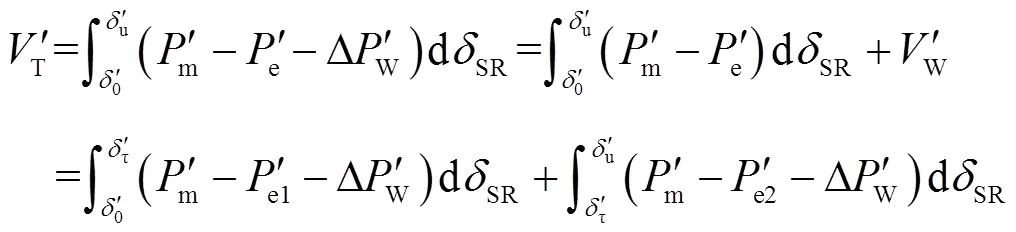
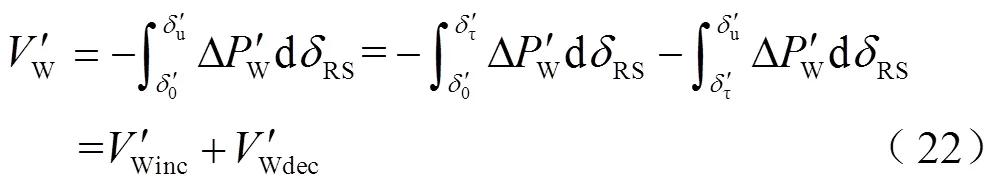
基于能量觀點的功角穩定性統一分析理論[23]，當系統遭受大干擾或小干擾時（以下統稱“擾動”），系統暫態能量T表示為

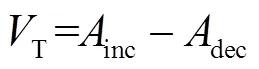
式中，inc、dec分別為系統功角首擺期間系統加速及減速面積。

4 DFIG等效慣量控制比例系數對系統功角首擺穩定性的影響機理

4.1 系統加速階段-功角首擺穩定機理分析

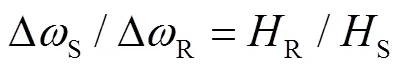
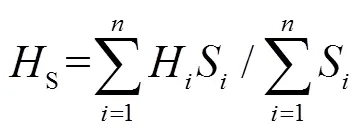
由式（13）可知，加速過程中DFIG提供的暫態能量Winc進一步化簡為

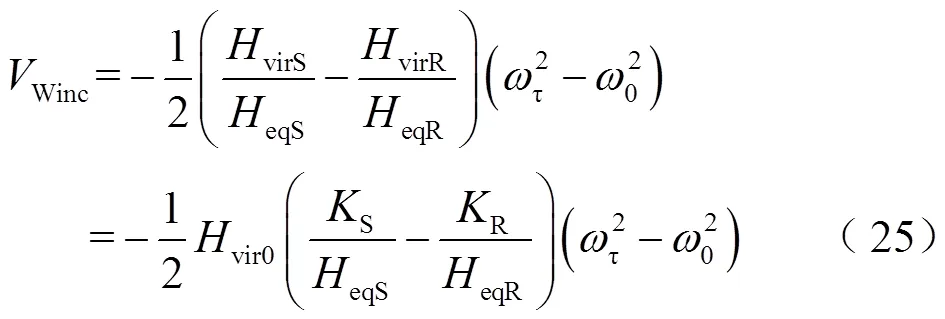
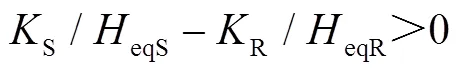
4.2 系統減速階段-功角首擺穩定機理分析

DFIG在系統減速過程中提供的暫態能量Wdec可表示為

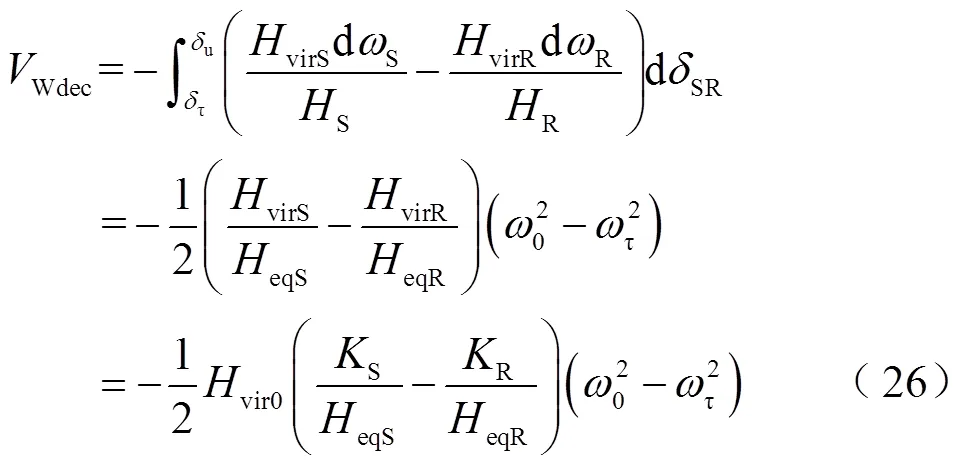
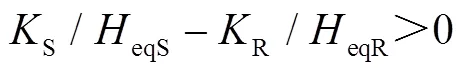
系統功角正向及反向擺動時，系統加速及減速階段系統功角首擺穩定性判別方式見表1、表2。

表1 系統功角正向擺動時功角首擺穩定性判別

Tab.1 The stability criterion of the first swing of power angle

表2 系統功角反向擺動時功角首擺穩定性判別

Tab.2 The stability criterion of the first swing of power angle

5 算例分析

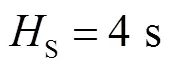
為評估不同場景下系統功角首擺穩定性，采用系統功角首擺最大偏移量的絕對值|ΔSR_max|作為系統功角穩定評估的指標。當|ΔSR_max|減小時，系統功角首擺穩定性增強；反之，系統功角首擺穩定性減弱。

表3 單臺風電機組參數

Tab.3 Parameters of DFIG

表4 單臺同步機參數

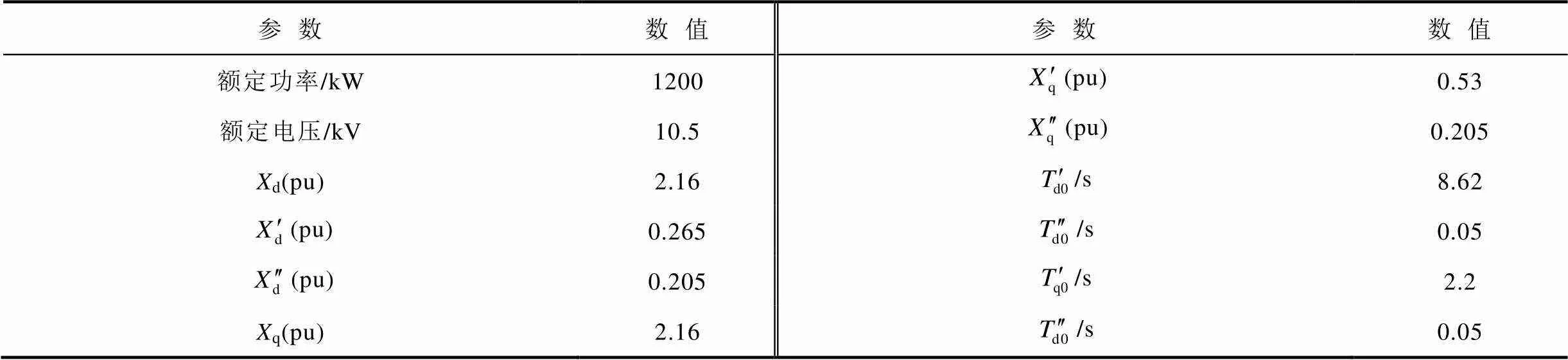
Tab.4 Parameters of synchronous generators

算例在系統受到大擾動（三相短路）及小擾動（負荷突增）時，根據DFIG等效慣量控制環節比例系數的不同分別設置五個不同場景，具體參數見表5。

表5 DFIG等效虛擬慣量控制環節比例系數

Tab.5 Equivalent proportional coefficient of virtual inertia control of DFIG

5.1 三相短路故障的系統功角首擺穩定性仿真分析

不同場景下，雙饋風機和同步發電機輸出電磁功率見表6。

表6 系統發生三相短路時同步發電機有功功率

Tab.6 Active power output of generators when three-phase short circuit occurs

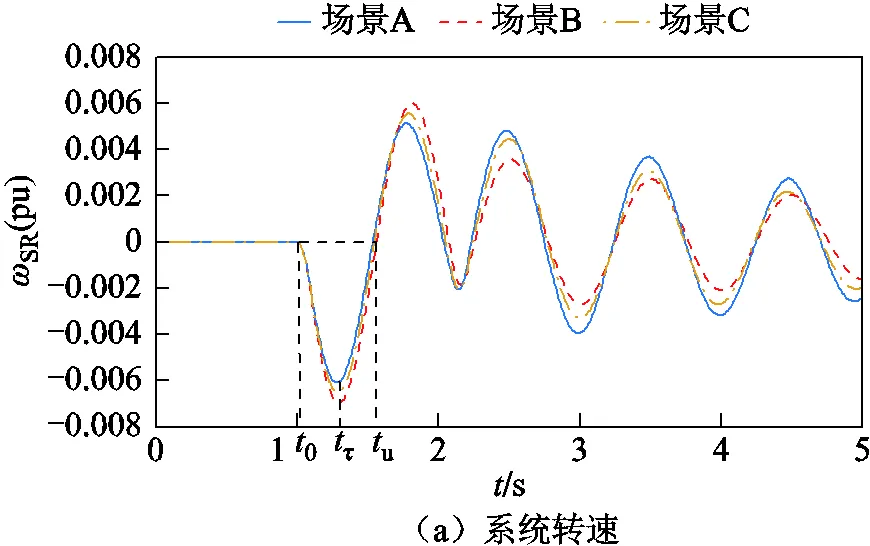
負荷L1、L2有功功率分別為1100MW和200MW，設置母線B8發生三相接地短路故障，故障持續時間0.1s，故障前后系統頻率、系統轉速、風機有功功率及系統功角波動情況如圖5所示，系統功角首擺穩定性評估結果見表7。

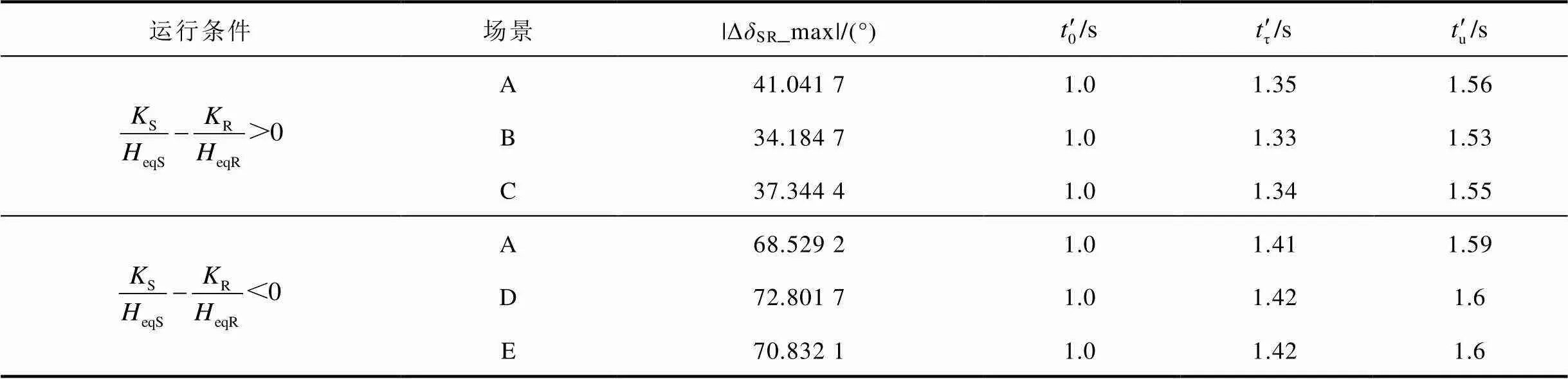
表7 三相短路時系統功角首擺穩定性評估指標及系統加速和減速階段時間

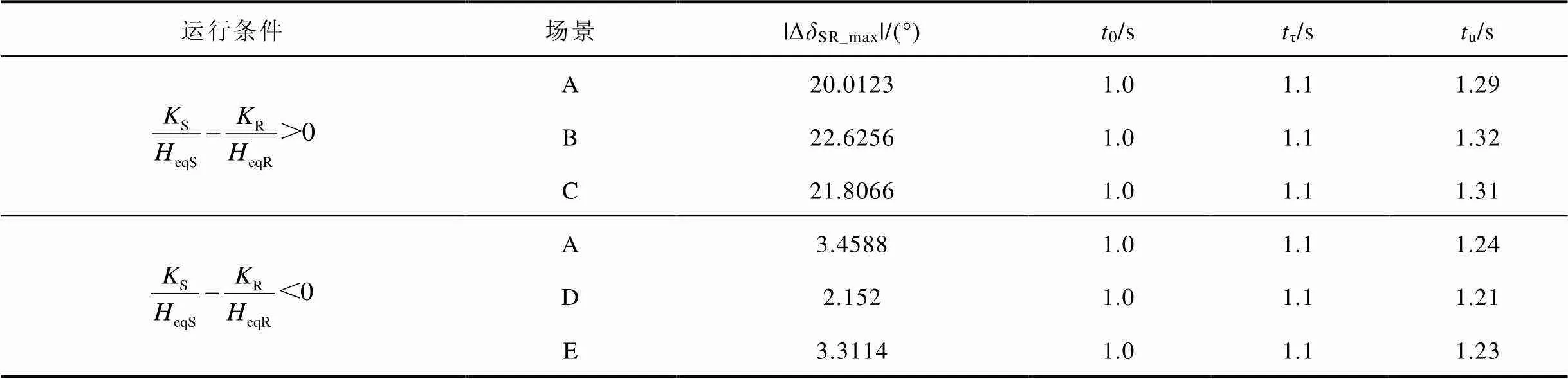
Tab.7 Stability evaluation index and acceleration and deceleration time of the system under three-phase short circuit

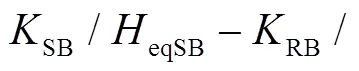
由表7可知，場景B、場景C情況下功角最大首擺偏移量絕對值|ΔSR_max|比場景A情況下增加2.613 3°和1.794 3°，表明系統發生三相短路故障時，DFIG等效慣量控制比例系數大于零使得系統功角首擺穩定性減弱，且DFIG等效慣量控制比例系數絕對值增加不利于系統功角首擺穩定。

負荷L1、L2有功功率分別為200MW和1 100MW，設置母線B8處發生三相接地短路故障，持續時間0.05s，故障前后系統頻率、系統轉速、聯絡線功率、風機有功輸出及系統功角波動情況如圖6所示，系統功角首擺穩定性評估結果見表7。

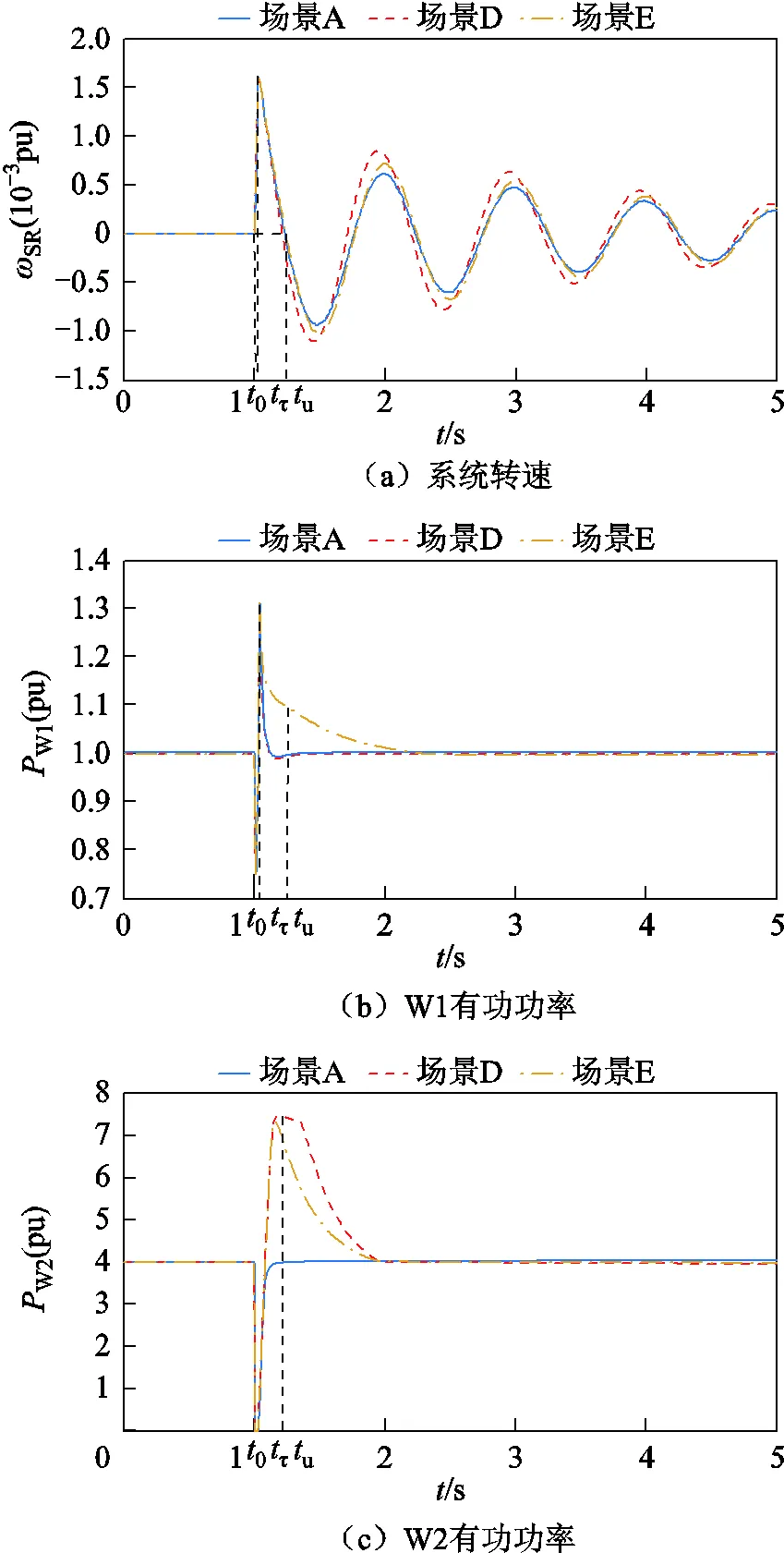
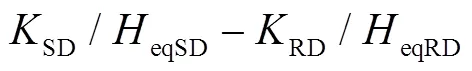
由表7可知，場景D、場景E情況下功角最大首擺偏移量絕對值|ΔSR_max|比場景A情況下減小1.306 8°和1.159 4°，表明系統發生三相短路故障時，DFIG等效慣量控制比例系數小于零使得系統功角首擺穩定性增強，且DFIG等效慣量控制比例系數絕對值增加有利于系統功角首擺穩定。

5.2 負荷突增的系統功角首擺穩定性仿真分析

負荷L1、L2有功功率分別為800MW和300MW，設置1.0～2.0s負荷L2增加500MW，系統功角反向擺動。擾動前后系統頻率、系統轉速、風機有功輸出及系統功角波動情況如圖7所示，系統功角首擺穩定性評估結果見表8。

表8 負荷突增時時系統功角首擺穩定性評估指標及系統加速及減速階段時間

Tab.8 Stability evaluation index and acceleration and deceleration time of the system during load sudden change

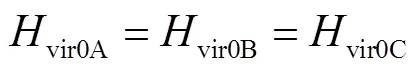
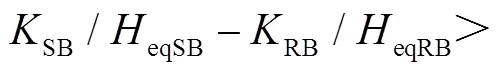
由表8可知，場景B、場景C情況下功角最大首擺偏移量絕對值|ΔSR_max|比場景A情況下減小7.153 89°和3.994 03°，系統功角首擺穩定性增強，且DFIG等效慣量控制比例系數增加有利于系統功角首擺穩定。

負荷L1、L2有功功率分別為300MW和800MW，設置1.0～2.0s負荷L1突增800MW，系統功角反向擺動。擾動前后系統頻率、系統轉速、風機有功輸出及系統功角波動情況如圖8所示，系統功角首擺穩定性評估結果見表8。

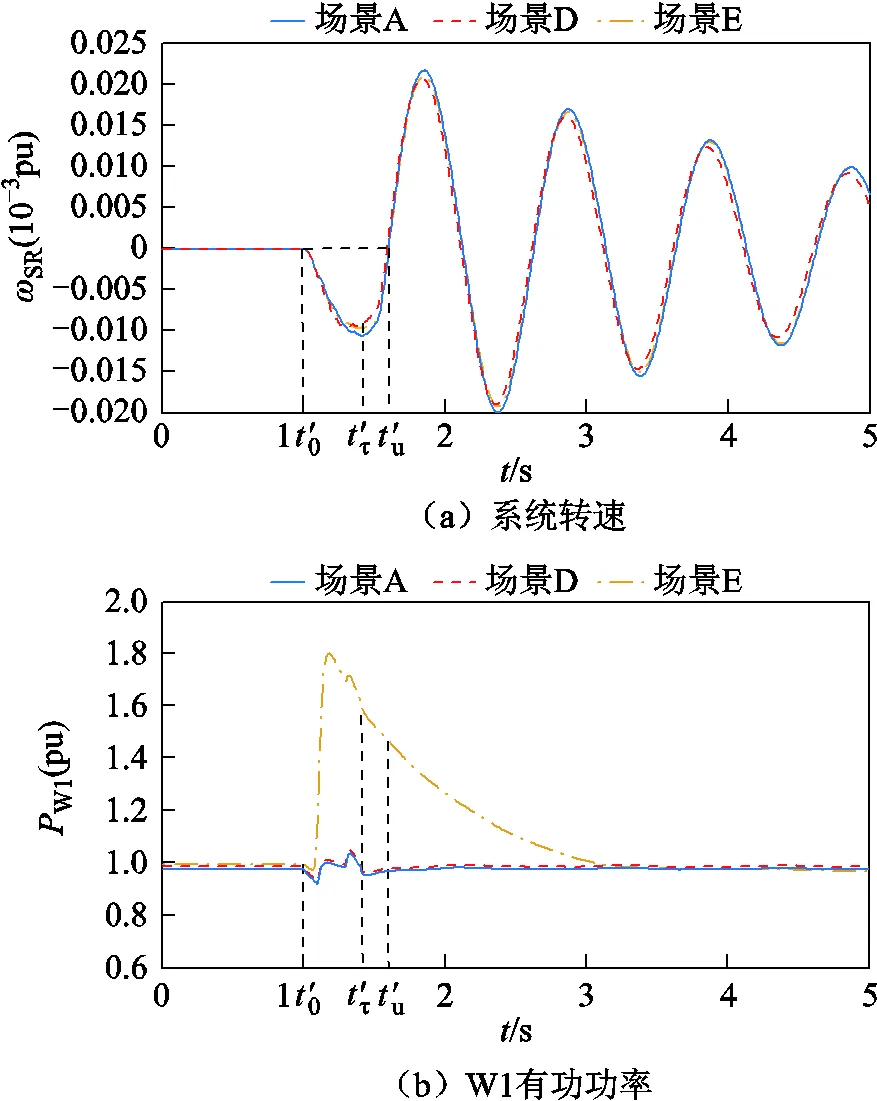
由表8可知，場景D、場景E情況下系統功角最大首擺偏移量絕對值|ΔSR_max|比場景A情況下增加4.272 5°和2.302 9°，系統功角首擺穩定性減弱，且DFIG等效慣量控制比例絕對值增加不利于系統功角首擺穩定。

6 結論

本文研究送受端區域內DFIG同時附加虛擬慣量控制，系統發生三相短路故障及負荷突增時，兩區域互聯系統DFIG等效慣量控制比例系數對系統加速及減速過程中暫態能量的影響，進而研究系統功角首擺穩定的內在機理，并通過系統功角首擺最大偏移量對系統功角首擺穩定性進行評估，分析結果表明：

1）系統發生三相短路故障時，系統功角正向擺動，DFIG慣量響應改變系統減速期間暫態能量，若兩區域互聯系統DFIG等效慣量控制環節比例系數大于零，系統功角首擺穩定性減弱，且DFIG等效慣量控制環節比例系數絕對值減小有利于系統功角首擺穩定；反之，不利于系統功角首擺穩定。

2）系統負荷突增時，系統功角反向擺動，DFIG慣量響應改變系統加速及減速期間暫態能量，若兩區域互聯系統DFIG等效慣量控制環節比例系數大于零，系統功角首擺穩定性增強，且DFIG等效慣量控制環節比例系數絕對值增加有利于系統功角首擺穩定；反之，不利于系統功角首擺穩定。

[1] Liu Juelin, Yang Zhifang, Yu Juan, et al. Coordinated control parameter setting of DFIG wind farms with virtual inertia control[J]. International Journal of Electrical Power & Energy Systems, 2020, 122(12): 106167.

[2] 章艷, 高晗, 張萌. 不同虛擬同步機控制下雙饋風機系統頻率響應差異研究[J]. 電工技術學報, 2020, 35(13): 2889-2900.

Zhang Yan, Gao Han, Zhang Meng. Research on frequency response difference of doubly-fed induction generator system controlled by different virtual synchronous generator controls[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2889-2900.

[3] 趙晶晶, 李敏, 何欣芹, 等. 基于限轉矩控制的風儲聯合調頻控制策略[J]. 電工技術學報, 2019, 34(23): 4982-4990.

Zhao Jingjing, Li Min, He Xinqin, et al. Coordinated control strategy of wind power and energy storage in frequency regulation based on torque limit control[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4982-4990.

[4] 顏湘武, 宋子君, 崔森, 等. 基于變功率點跟蹤和超級電容器儲能協調控制的雙饋風電機組一次調頻策略[J]. 電工技術學報, 2020, 35(3): 530-541.

Yan Xiangwu, Song Zijun, Cui Sen, et al. Primary frequency modulation strategy of doubly-fed induction generator based on variable power point tracking and coordinated control of supercapacitor energy storage[J]. Transactions of China Electrote-chnical Society, 2020, 35(3): 530-541.

[5] 顏湘武, 王德勝, 楊琳琳, 等. 直驅風機慣量支撐與一次調頻協調控制策略[J]. 電工技術學報, 2021, 36(15): 3282-3292.

Yan Xiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support and primary frequency regulation of PMSG[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3282-3292.

[6] 郝正航. 雙饋風電機組的暫態行為及其對電力系統穩定性影響[D]. 天津: 天津大學, 2011.

[7] 張祥宇, 王爽, 王毅, 等. 含可控慣量發電系統的功角暫態穩定分析與慣性控制策略[J]. 電力建設, 2018, 39(1): 106-112.

Zhang Xiangyu, Wang Shuang, Wang Yi, et al. Power angle transient stability analysis and inertia control strategy of power generation system with controllable inertia[J]. Electric Power Construction, 2018, 39(1): 106-112.

[8] 劉斯偉. 并網雙饋風電機組對電力系統暫態穩定性的影響機理研究[D]. 北京: 華北電力大學(北京), 2016.

[9] 趙振元, 陳維榮, 戴朝華, 等. 系統慣性時間常數對互聯電網暫態穩定水平的影響[J]. 電網技術, 2012, 36(1): 102-107.

Zhao Zhenyuan, Chen Weirong, Dai Chaohua, et al. Influence of system inertia time constant on transient stability level of interconnected power grid[J]. Power Syetem Technology, 2012, 36(1): 102-107.

[10] 張明理, 徐建源, 李佳玨. 含高滲透率風電的送端系統電網暫態穩定研究[J]. 電網技術, 2013, 37(3): 740-745.

Zhang Mingli, Xu Jianyuan, Li Jiajue. Research on transient stability of sending power grid containing high proportion of wind power[J]. Power Syetem Technology, 2013, 37(3): 740-745.

[11] 王哲. 慣量可控發電機組對電力系統動態特性影響分析[D]. 北京: 華北電力大學(北京), 2019.

[12] Kimbark E W. Power system stability: synchronous machines[J]. New York: John Wiley, 1948.

[13] 羅遠翔, 楊仁剛, 蔡國偉, 等. 大容量風電接入系統對網絡暫態能量的影響[J]. 電力系統及其自動化學報, 2014, 28(1): 76-80.

Luo Yuanxiang, Yang Rengang, Cai Guowei, et al. Influence of large capacity wind power access system on network transient energy[J]. Proceedings of the CSU-EPSA, 2014, 28(1): 76-80.

[14] 姜惠蘭, 姜哲, 李天鵬, 等. 風機轉子撬棒投切對電力系統暫態穩定性的影響[J]. 電網技術, 2016, 40(8): 2383-2388.

Jiang Huilan, Jiang Zhe, Li Tianpeng, et al. Impact of rotor crowbar switching on transient stability of power system[J]. Power System Technology, 2016, 40(8): 2383-2388.

[15] 吳玉璋. 風電場接入對電力系統暫態穩定影響研究[D]. 天津: 天津大學, 2017.

[16] 羅遠翔, 楊仁剛, 劉鋮, 等. TCSC提高大容量風電接入系統的穩定性及控制策略[J]. 電測與儀表, 2014(4): 35-39.

Luo Yuanxiang, Yang Rengang, Liu Cheng, et al. Control strategy of TCSC for stability improvement in power systems integrated with large scale wind farms[J]. Electrical Measurement & Instrumentation, 2014(4): 35-39.

[17] 周明, 董哲, 李洪宇, 等. 風機故障后有功控制對系統暫態功角失穩的影響機理（英文）[J]. 電網技術, 2019, 43(4): 1280-1293.

Zhou Ming, Dong Zhe, Li Hongyu, et al. Influence mechanism of active power control on transient angle instability of wind turbine system after fault[J]. Power System Technology, 2019, 43(4): 1280-1293.

[18] 于珍, 沈沉, 張雪敏. 雙饋風機故障穿越后功率恢復速率對系統暫態穩定的影響分析[J]. 中國電機工程學報, 2018, 38(13): 3781-3791, 4019.

Yu Zhen, Shen Shen, Zhang Xuemin. Influence of power recovery rate on transient stability of doubly-fed fan after fault crossing[J]. Proceedings of the CSEE, 2018, 38(13): 3781-3791, 4019.

[19] 牟澎濤, 趙冬梅, 王嘉成. 大規模風電接入對系統功角穩定影響的機理分析[J]. 中國電機工程學報, 2017, 37(5): 1325-1334.

Mou Pengtao, Zhao Dongmei, Wang Jiacheng. Mechanism analysis of influence of large-scale wind power access on system power angle stability[J]. Proceedings of the CSEE, 2017, 37(5): 1325-1334.

[20] 林俐, 楊以涵. 基于擴展等面積定則的含大規模風電場電力系統暫態穩定性分析[J]. 電力系統保護與控制, 2012, 40(12): 105-110, 115.

Lin Li, Yang Yihan. Transient stability analysis of power system with large scale wind farm based on extended equal area rule[J]. Power System Protection and Control, 2012, 40(12): 105-110, 115.

[21] 李世春, 鄧長虹, 龍志君, 等. 風電場等效虛擬慣性時間常數計算[J]. 電力系統自動化, 2016, 40(7): 22-29.

Li Shichun, Deng Changhong, Long Zhijun, et al. Calculation of equivalent virtual inertia time constant of wind farm[J]. Automation of Electric Power Systems, 2016, 40(7): 22-29.

[22] 劉皓明, 任秋業, 張占奎, 等. 雙饋風機等效慣性時間常數計算及轉差率反饋慣量控制策略[J]. 電力系統自動化, 2018, 42(17): 49-57.

Liu Haoming, Ren Qiuye, Zhang Zhankui, et al. Calculation of equivalent inertia time constant and control strategy of slight feedback inertia for double-fed fan[J]. Automation of Electric Power Systems, 2018, 42(17): 49-57.

[23] 李春艷, 孫元章, 彭曉濤, 等. 采用廣域測量信息反饋的廣域PSS參數設計[J]. 電力系統自動化, 2009, 33(18): 6-11.

Li Chunyan, Sun Yuanzhang, Peng Xiaotao, et al. Wide-area PSS parameter design using wide-area measurement feedback[J]. Automation of Electric Power Systems, 2009, 33(18): 6-11.

[24] Zhang Xiangyu, Zhu Zhengzhen, Fu Yuan, et al. Multi-objective virtual inertia control of renewable power generator for transient stability improvement in interconnected power system[J]. International Journal of Electrical Power and Energy Systems, 2020, 117: 105641.1-105641.12.

[25] Shao Haoshu, Cai Xu, Zhou Dangsheng, et al. Equivalent modeling and comprehensive evaluation of inertia emulation control strategy for DFIG wind turbine generator[C]//2019 10th International Conference on Power Electronics and ECCE Asia, Busan, 2019: 3164-3170.

[26] 袁輝, 宋曉喆, 孫福壽, 等. 弱電網中低電壓穿越控制策略導致的雙饋風機失穩機理分析[J]. 電力自動化設備, 2020, 40(9): 50-58.

Yuan Hui, Song Xiaozhe, Sun Fushou, et al. Analysis on instability mechanism of double-fed fan caused by low voltage crossing control strategy in weak power grid[J]. Electric Power Automation Equipment, 2020, 40(9): 50-58.

[27] 張磊, 張闖, 羅毅, 等. 電網友好型雙饋感應發電機的暫態協調控制策略[J]. 電力系統自動化, 2019, 43(12): 44-50, 112.

Zhang lei, Zhang Chuang, Luo Yi, et al. Transient coordinated control strategy of grid friendly double-fed induction generator[J]. Automation of Electric Power Systems, 2019, 43(12): 44-50, 112.

（編輯 赫蕾）

Mechanism Analysis of Effect of Equivalent Proportional Coefficient of Inertia Control of DFIG on Stability of First Swing of Power Angle

Wang Ke Qin Wenping Zhang Yu Zhu Zhilong Xue Shaokai

（Shanxi Key Laboratory of Power System Operation and Control Taiyuan University of Technology Taiyuan 030024 China）

Compared with traditional synchronous machines, doubly-fed Induction Generator (DFIG) lacks inertial response capability. Therefore, when a large-scale DFIG is connected to a power system suffering from large or small disturbances (three-phase short circuit, sudden load increase, etc.), the system inertial response capability is severely lacking and the problem of transient power angle stability is highlighted. With the continuous improvement of the DFIG virtual inertia control technology, the DFIG can provide dynamic inertia support for the system. Therefore, there is an urgent necessity to carry out research on the mechanism of the effect of the DFIG’s virtual inertia on the first swing stability of the system power angle. To address these issues, this paper proposes a mechanism analysis method for the effect of equivalent proportional coefficient of virtual inertia control of DFIG on stability of first swing of power angle.

Firstly, the equivalent model of two regional inertia centers is derived, and the influence of DFIG virtual inertia on the rotor motion equations of the two regions is analyzed. Secondly, from the perspective of the transient energy of the system, the influence of the equivalent proportional coefficient of virtual inertia control of DFIG in the two regions on the transient energy during the acceleration and deceleration of the system is studied when the swing direction of system power angle are different and the swing direction of influence mechanism on the first swing stability of system is further studied. Finally, the stability of the system was evaluated by the maximum deviation of the system power angle and a simulation model of the two-region interconnection system was built in PSASP to verify the proposed theory.

Considering the DFIG in sending and receiving ends with additional inertia control, the following conclusions can be drawn from the simulation analysis: ①When a three-phase short circuit fault occurs in the system, the power angle of the system swings in the positive direction, and the DFIG inertia response changes the transient energy during system deceleration. If the equivalent proportional coefficient of the DFIG’s virtual inertia control link is greater than zero, the stability of the system power angle first swing is weakened, and the absolute value of the equivalent proportional coefficient of the DFIG’s virtual inertia control link is reduced, which is conducive to the stability of the system power angle first swing, otherwise, it is not conducive to the stability of the system power angle first swing. ②When the system load suddenly increases, the power angle of the system swings in the opposite direction, and the DFIG inertia response changes the transient energy during the system acceleration and deceleration. If the equivalent proportional coefficient of the DFIG’s virtual inertia control link is greater than zero, the stability of the system power angle first swing is enhanced, and the absolute value of the equivalent proportional coefficient of the DFIG’s virtual inertia control link is increased, which is conducive to the stability of the system power angle first swing, otherwise, it is not conducive to the stability of the system power angle first swing.

Doubly-fed induction generator(DFIG), equivalent proportional coefficient of virtual inertia control, transient energy function, the first swing stability of power angle

10.19595/j.cnki.1000-6753.tces.211305

TM614

國家自然科學基金聯合基金重點項目（U1910216）和山西省科技重大專項（20181102028）資助。

2021-08-17

2021-11-18

王 科 女，1995年生，碩士研究生，研究方向為新能源電力系統分析與控制。E-mail：15536816118@163.com

秦文萍 女，1972年生，教授，博士生導師，研究方向為電力系統可靠性/穩定性分析、微電網運行與控制、交直流混合微電網保護等。E-mail：qinwenping@tyut.edu.cn（通信作者）

（編輯 赫蕾）