考慮風電場量測相關性的雙饋風力發電機魯棒動態狀態估計

朱茂林 劉 灝 畢天姝

考慮風電場量測相關性的雙饋風力發電機魯棒動態狀態估計

朱茂林 劉 灝 畢天姝

（新能源電力系統國家重點實驗室（華北電力大學） 北京 102206）

基于相量測量單元（PMU）的風力發電機動態狀態估計能夠為風電場能量管理系統提供實時可靠的數據基礎。然而，目前多數風電場不具備為每臺風機都安裝PMU的量測條件，且動態狀態估計易受不良數據及擾動的影響。針對上述問題，提出一種考慮風電場量測相關性的雙饋風機魯棒動態狀態估計方法。在用最少數量的PMU實現風電場所有節點可觀的基礎上，提出基于PMU量測空間相關性和風機動態模型時間相關性的冗余量測集構造方法，進而利用加權最小絕對值魯棒估計得到所有風機的機端電氣量，并濾除不良數據。考慮到擾動時狀態預報值不準確，提出了基于過程噪聲尺度因子的魯棒濾波方法，在擾動時降低不準確預報值的權重。仿真表明，所提方法對量測配置要求低，并能準確估計風電場內單臺風機的動態狀態。

雙饋風機 動態狀態估計 量測相關性 最小絕對值估計 魯棒容積卡爾曼濾波

0 引言

在落實“碳達峰、碳中和”目標的大背景下，風電的開發利用必然會更加受到重視。然而風電具有強間歇性、隨機波動性和低可調度性的特點[1]，風電場側能量管理系統（Energy Management System, EMS）可抑制風電波動對電網的影響，提高風電利用率[2]。相量測量單元（Phasor Measurement Unit, PMU）能夠實現快速同步量測，使動態狀態估計（Dynamic State Estimation, DSE）成為可能[3]。DSE能在量測系統主站提高量測數據質量，并通過卡爾曼濾波的預報-濾波框架實時估計風機等動態元件的運行狀態，進而用于風電場優化控制等EMS高級應用[4]，對風電場全狀態感知具有重要意義。

雙饋式風力發電機組（Doubly-Fed Induction Generator, DFIG）因其良好的經濟性和運行特性成為風電場主力機型之一，本文選擇其作為風電場DSE的研究對象。目前DFIG動態狀態估計的相關文獻[5-7]大多使用風電場等值模型，然后利用風電場并網點處的同步相量量測對該等效模型進行DSE。文獻[5]假設DFIG等值模型的換流器輸出電壓可量測并作為DSE的輸入，這對于等效模型難以實現。文獻[6-7]用包括換流器控制系統在內的DFIG詳細模型作為風電場等效模型，然而該等效模型控制器參數的準確獲取是一個棘手問題。隨著新能源占比的提高及測量技術的發展，已有針對風機等新能源電源的PMU，如新能源場站同步測量裝置（Synchronized Measurement Device for Renewables, SMD-R）[8]等，與現有輸電網PMU相比，其測量頻帶更寬，上傳速率更快，可安裝在風電場內部，基于此，可對風場內的單臺風機進行DSE。然而，單臺DFIG的DSE需要其機端電氣量作為狀態估計器的輸入和量測，但風電場內風機數量眾多，目前每臺DFIG都裝有PMU的量測配置并未普及，DFIG本身的量測也只用于本地控制且非同步相量量測，因此存在DSE量測要求難以滿足的問題。

常用非線性卡爾曼濾波方法包括擴展卡爾曼濾波[9]、無跡卡爾曼濾波[7]、容積卡爾曼濾波（Cubature Kalman Filter, CKF）[10]及粒子濾波[11]，其中容積卡爾曼濾波無截斷誤差，不需選擇任何參數且算法效率和精度較高，因此本文基于CKF對DFIG進行狀態估計。然而，在電力系統實際運行中，由于缺乏校準、硬件故障或脈沖噪聲等原因，PMU會出現不良數據，上述方法易受不良數據的影響。文獻[12]利用殘差檢測和迭代排除的方式辨識并濾除量測中的不良數據。文獻[13-14]基于新息異常來調整量測噪聲方差陣，進而抑制量測不良數據的影響。但上述方法未考慮同樣由PMU量測得來的估計器輸入也有可能存在不良數據的問題。此外，卡爾曼濾波需要根據前一時刻狀態估計值進行狀態預報，但 DFIG容量小且采用電力電子裝置控制，擾動后狀態變化迅速[15]，因此擾動時的狀態預報值可能存在較大偏差，進而影響狀態估計結果。

針對上述問題，本文提出一種考慮風電場量測相關性的DFIG魯棒動態狀態估計方法。首先，考慮到風電場本身可視為一個小型輻射狀電網，基于風電場的拓撲特點對PMU進行最優配置，并結合DFIG時間維度的動態模型約束信息構造冗余量測集。其次，基于該冗余量測集和加權最小絕對值（Weighted Least Absolute Value, WLAV）估計得到所有DFIG的機端電氣量，并利用擾動和不良數據的判別以及WLAV方法的魯棒性濾除DSE輸入和量測中的不良數據。然后，在擾動時引入過程噪聲尺度因子調整過程噪聲方差陣，從而降低預報值對狀態估計結果的影響。最后，搭建DFIG風電場仿真模型，驗證所提方法的有效性。

1 DFIG模型及不良數據影響分析

1.1 DFIG動態狀態估計模型

DFIG動態模型由風輪及傳動系、異步電機、轉子側和網側換流器及其控制器、直流電容以及濾波電感等部分組成，其具體結構如圖1所示。本文使用DFIG的相量模型，采用電動機慣例，所有電流相量以流入DFIG為正方向。

風輪及傳動系統的單質塊模型為

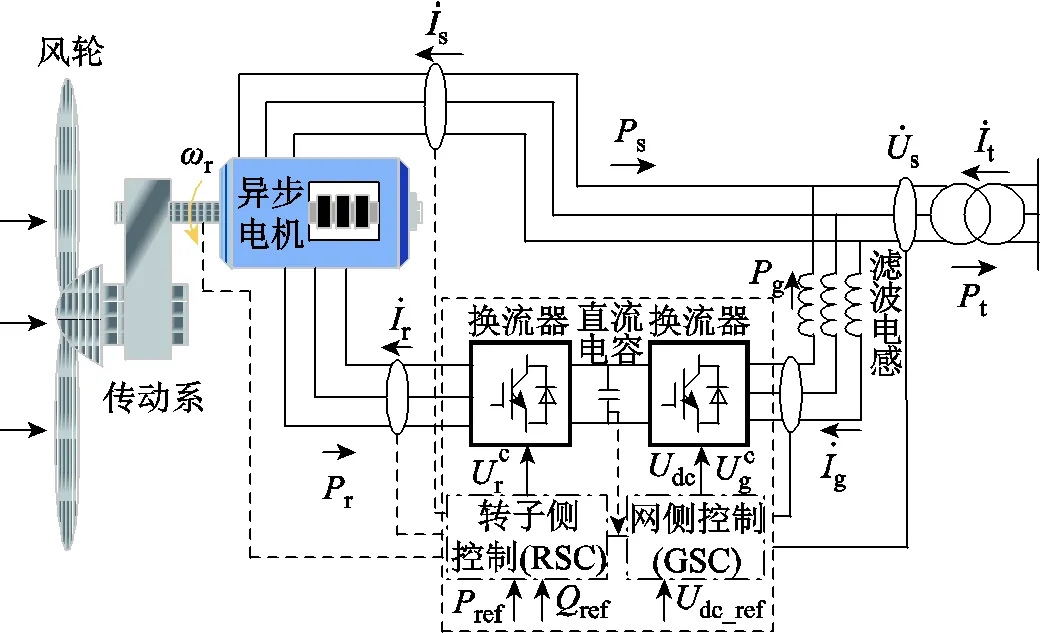
圖1 雙饋風力發電機結構

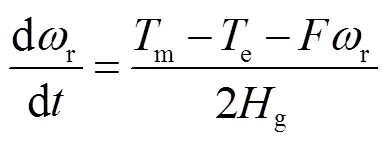
式中，r為轉子轉速；m為風輪輸出的機械轉矩，與風速wind有關；e為電磁轉矩；為摩擦系數；g為軸系等效慣性時間常數。

電機定子磁通ds、qs及轉子磁通dr、qr的動態變化為

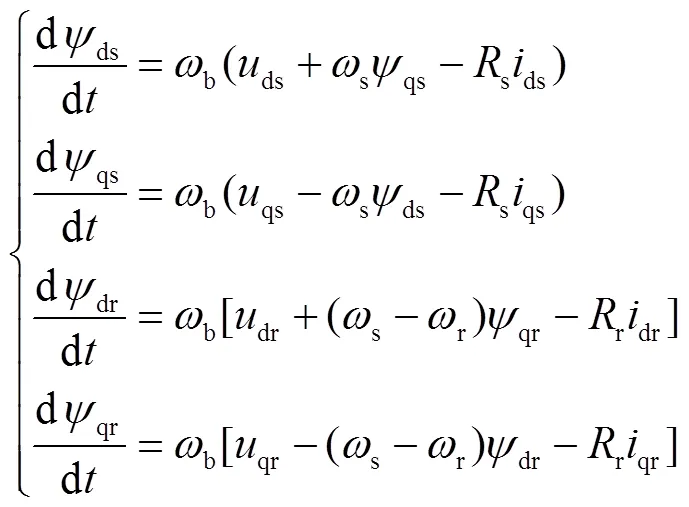
式中，b為角速度基準值；s為同步轉速標幺值；s和r分別為定子和轉子的電阻；下標s表示定子側電氣量；下標r表示轉子側電氣量；ds、qs分別為DFIG機端電壓的d、q軸分量，其作為DSE的輸入將DFIG與外部網絡解耦；ds、qs分別為DFIG 定子電流的d、q軸分量；dr、qr分別為DFIG 轉子電壓的d、q軸分量；dr、qr分別為DFIG 轉子電流的d、q軸分量。

DFIG的轉子側換流器主要控制DFIG輸出的有功功率和無功功率，網側換流器負責保持直流電容電壓穩定，其控制指令由PI控制器給出，對應的積分環節狀態變量用1～7表示，其控制框圖及1～7的具體定義見附錄。此外，直流電容和濾波電感的動態方程為

式中，dc為直流電容電壓；r和g分別為換流器轉子側和網側功率；dc為直流電容；下標g表示換流器網側電氣量；dg、qg分別為換流器網側電壓的d、q軸分量；dg、qg分別為換流器網側電流的d、q軸分量；g和g分別為濾波電感的電阻和電抗。式（1）～式（4）組成DSE的狀態轉換方程()。

對于量測方程，結合DFIG狀態估計的能觀性需求及PMU可提供的量測量，選擇DFIG機端電流dt、qt以及發電機輸出功率t、t作為量測量，則每臺DFIG動態狀態估計的量測方程()為

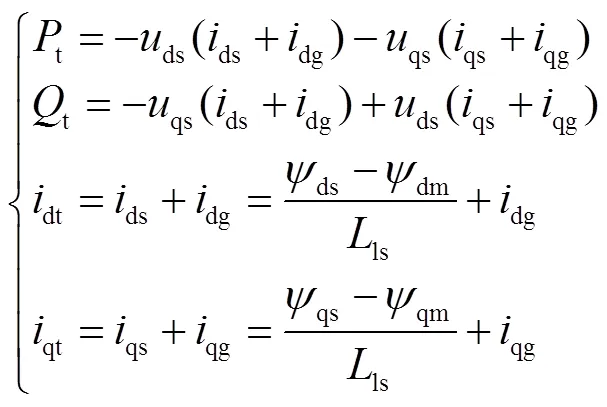
將上述DFIG連續動態模型離散化[16]，并寫為一般狀態空間形式，有

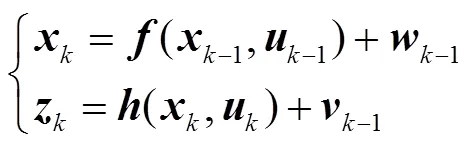
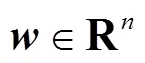
基于上述離散狀態空間模型，即可利用CKF算法對DFIG的動態狀態進行估計。

1.2 不良數據對CKF的影響分析

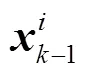
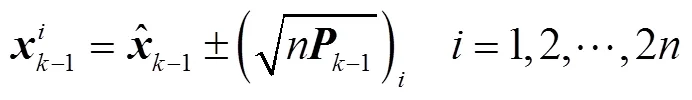
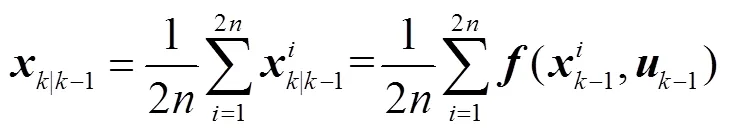
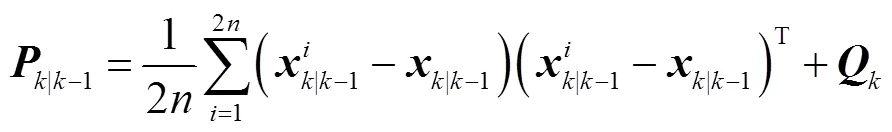
|k-1的準確性對DSE結果有較大影響。在上述過程中可能導致|k-1產生較大偏差的原因有：①DFIG機端電壓被視為輸入，以將DFIG與外部網絡解耦，然而由PMU量測得到的機端電壓中可能存在不良數據，進而使-1不準確；②由式（9）可知，|k-1由-1時刻的狀態和輸入計算得到，由于擾動無法預測，若在[-1,]這一時間段內發生擾動，DFIG的迅速響應會使其狀態迅速變化，導致-1與實際值存在較大偏差。

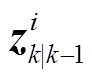
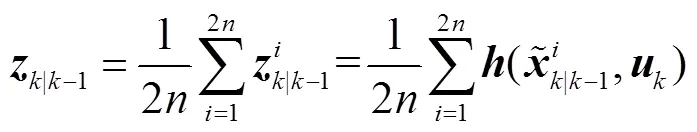
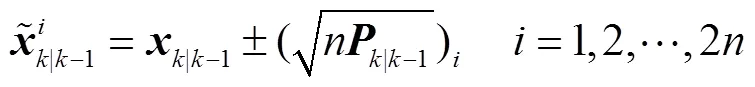
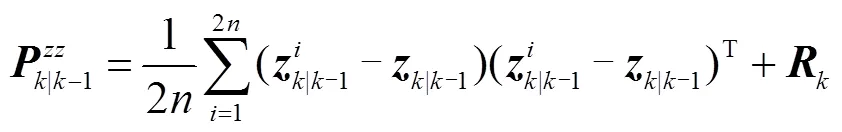
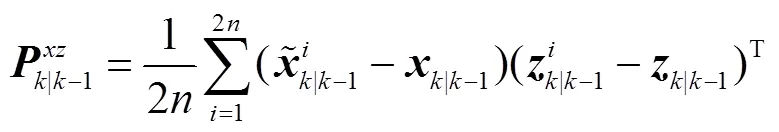
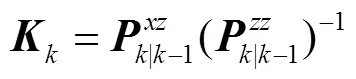
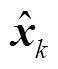
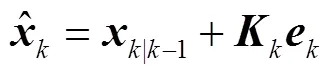
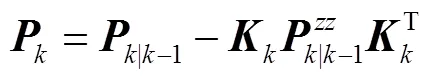
可知量測預報向量-1和PMU量測向量中的不良數據會導致異常，進而影響狀態估計結果。由式（12）可知，-1中的異常值主要來自-1及，而的不良數據主要來自PMU量測過程。

基于新息的量測不良數據處理方法[14]在假設輸入向量和狀態預報值|k-1準確的基礎上處理量測中的不良數據。然而，由上述分析可知，PMU的量測不良數據對輸入向量及量測向量都有影響，且擾動會使基于前一時刻狀態計算得到的|k-1不能及時跟隨實際狀態的變化，這些情況都會引起新息變大。因此僅基于異常判定量測中存在不良數據會導致對正常量測值的誤判。

2 風電場PMU最優配置及冗余量測集構造

針對風電場內量測配置不足的問題，本節通過PMU最優配置和量測空間相關性實現所有節點可觀，并利用DFIG動態狀態的時間相關性構造冗余量測集，為準確估計所有DFIG的機端電氣量提供量測基礎。

2.1 風電場PMU的最優配置

風電場典型拓撲如圖2所示，圖中的放射型連接是風電場集電系統的主要連接方式[17]，具有結構簡單經濟、運行方便的特點。從量測配置的角度看，風電場的放射狀結構與配電網結構[18]類似，含有較多的零注入節點和葉子節點（只與一個節點相連的節點，如風機箱變的低壓側），因此可將量測配置問題轉換為0-1型整數線性規劃問題。

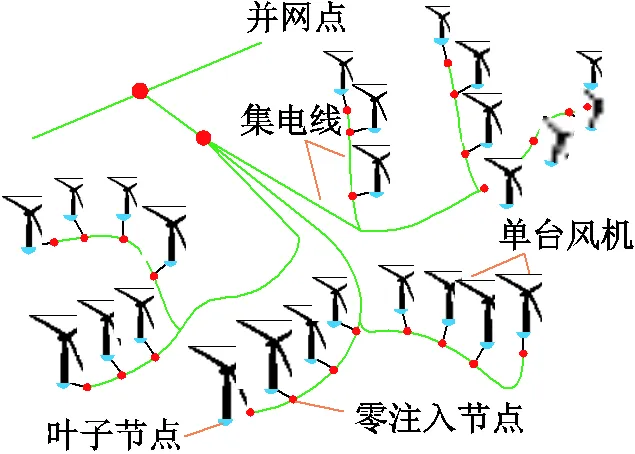
圖2 風電場典型拓撲

假設風電場共有個節點，則目標函數為

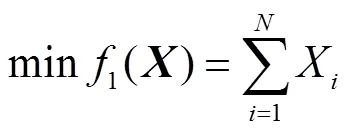
1）如果某節點配置PMU，則認為與其相連的節點可觀測，如式（19）中O表達式的前半部分所示。

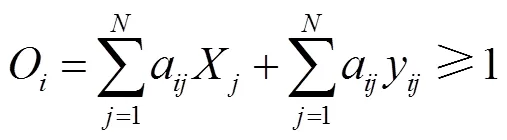
式中，O為節點被觀察到的次數，要求每個節點可觀則需O≥1；a為節點關聯矩陣的元素；y為零注入節點影響的二元輔助變量，y=1表示節點可根據基爾霍夫電流定律由零注入節點及其相連節點觀測。

2）零注入約束。假設某個零注入節點及其相連節點共+1個，若其中任意個節點可觀，則節點+1也可觀[19]，反映此特征的約束如式（19）和式（21）所示。

由于只有一個節點可從零注入節點及其相連節點的可觀性中受益，因此y要滿足式（21）。

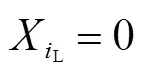
求解上述整數規劃問題，即可得到以使用最少數量的PMU實現所有節點可觀為目標的配置方案。

2.2 基于時空相關性的冗余量測集構造

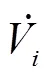
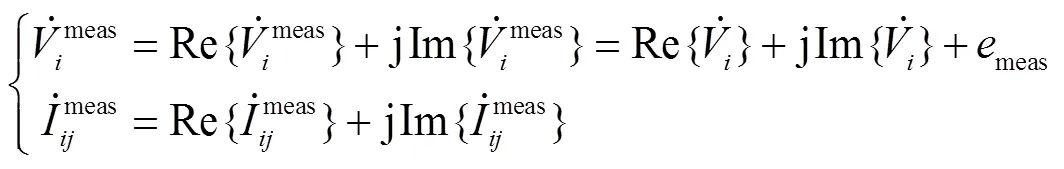
根據基爾霍夫電流定律，與零注入節點ZIB相連的條支路的電流之和為零，故定義虛擬量測為

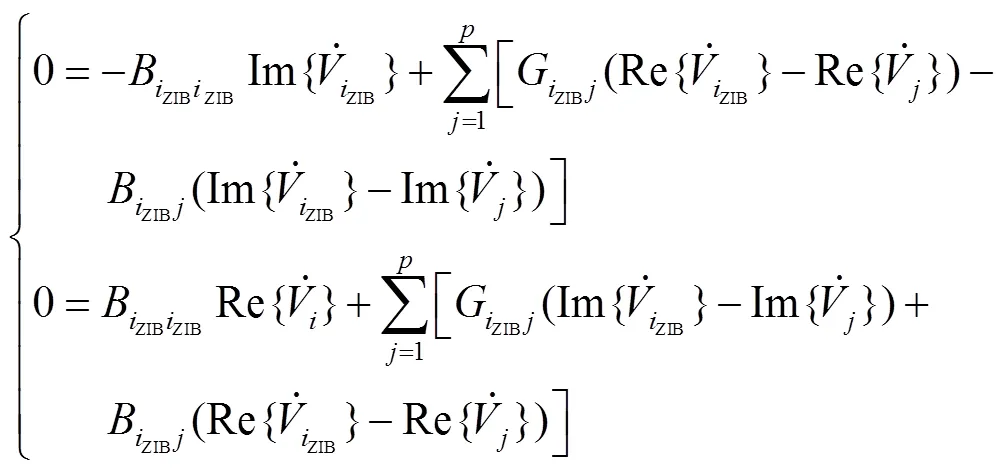
狀態估計需要利用量測冗余來提高估計準確性，而僅包含上述PMU量測和零注入虛擬量測的量測集冗余度較低。DFIG動態模型包含其狀態隨時間變化的規律，因此狀態具有時間相關性，可用于提高量測冗余。在得到各DFIG的狀態預報值之后，計算其各自輸出電流的預報值，并作為虛擬量測參與風電場DFIG機端電氣量估計。與的關系如式（25）所示，將其表示為，即

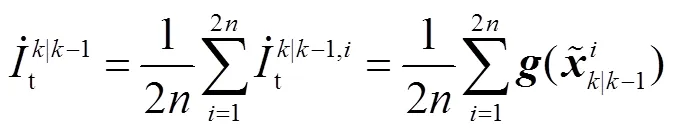
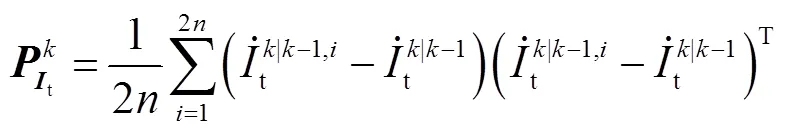
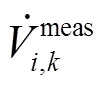
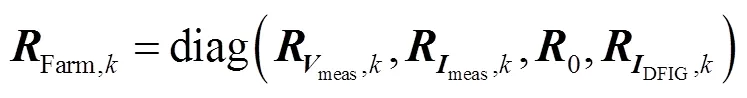
3 DFIG機端電氣量魯棒估計

輸入向量及量測向量中的不良數據都會導致新息異常，難以在DSE執行過程中對二者進行區分。針對該問題，在前述冗余量測集的基礎上，本節通過基于WLAV的魯棒方法來估計所有DFIG機端電氣量，在DSE之前濾除PMU量測不良數據。

3.1 擾動與量測不良數據判別

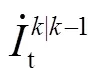
風電場內各DFIG機組間的電氣聯系較緊密，因此正常運行或擾動發生時各PMU的量測變化相似；當某臺PMU量測存在不良數據時，其他PMU出現類似行為的概率很小，即不良數據的空間相關性差。由此，本文對每臺PMU的量測數據進行突變檢測，如果多臺PMU檢測到突變，則認為是擾動數據；如果只有一臺PMU有突變，則認為該臺PMU產生了不良數據。

正常運行時，PMU測量信號相鄰量測點的變化很小，因此對PMU測量結果作差值絕對值運算，可認為其結果只包含噪聲信號；而當擾動發生或存在不良數據時，相鄰量測點的變化較大，則差值絕對值信號中將包含有噪聲與突變信號。因此，通過差值絕對值可以檢測突變，但需確定一個閾值，要求其既能濾除噪聲影響，也能準確檢測擾動或不良數據。考慮到固定閾值的適應性較差，文獻[21]提出了一種適用于電能質量擾動檢測的自適應閾值，本文將其擴展至相量量測信號，如式（29）所示。

式中，τ為時刻閾值；為量測噪聲統計標準差；mean為窗長內的量測幅值信號均值；為差值絕對值信號的方差。

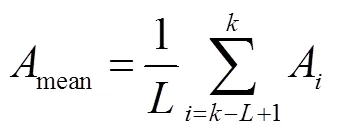
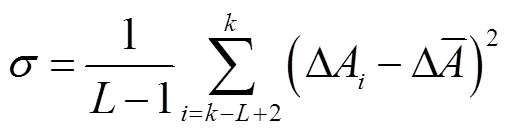
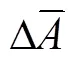
正常情況下量測中的噪聲穩定，只與噪聲有關，故其保持在較小范圍，進而閾值τ較大，差值絕對值不會超過閾值的范圍，即判別無突變；當出現擾動或存在不良數據時，差值絕對值增加，同時方差也會迅速增大，導致閾值減小，差值絕對值就會超出閾值線，即該臺PMU檢測到突變，若多臺PMU同時檢測到突變，則認為擾動發生，否則為不良數據。

3.2 基于WLAV的DFIG機端電氣量估計

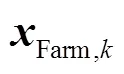
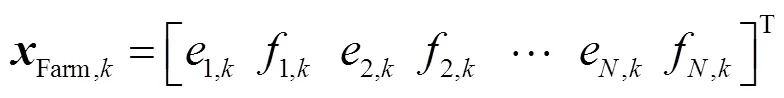
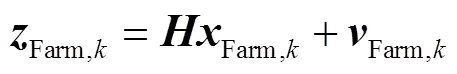
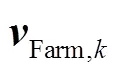
為進一步降低量測不良數據和擾動的影響，在前述降低權重的基礎上，采用具有良好抗差性能的WLAV[22]對DFIG機端電氣量進行估計，目標函數為

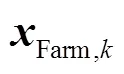
4 基于過程噪聲尺度因子的魯棒CKF

擾動發生時基于擾動前狀態計算得到的狀態預報值|k-1不能及時反映實際狀態變化，由于已經通過DFIG機端電氣量魯棒估計濾除了輸入向量及量測向量中的不良數據，因此當新息異常時，可認為是由|k-1偏離真實值導致的，基于此對CKF進行改進。

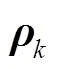
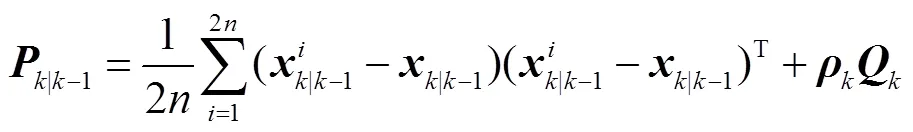
由式（6）可知，過程噪聲估計值應滿足

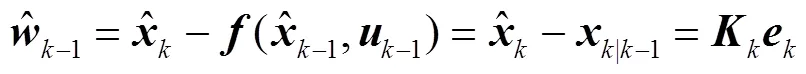
則其協方差矩陣估計值可表示為

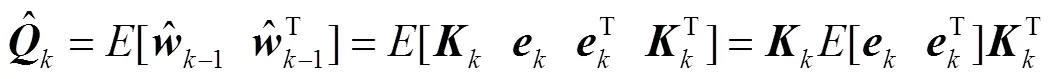
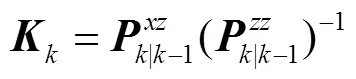
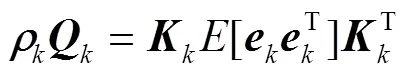
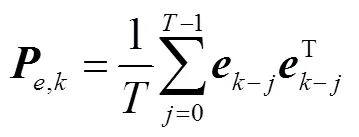
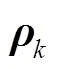
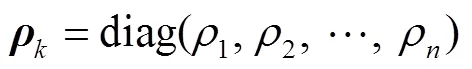
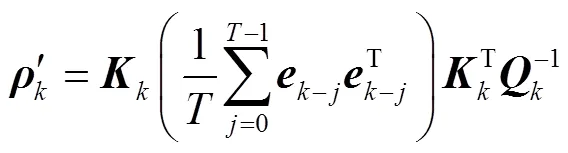
為方便實施，圖3給出了考慮風電場量測相關性的DFIG魯棒動態狀態估計流程。本文所提算法具體步驟總結如下：

1）初始化：輸入參數；利用式（18）～式（21）對風電場PMU進行最優配置；設定初始時刻狀態值0、誤差協方差矩陣0，令=1。

2）預報步：在時刻，利用式（8）～式（10）計算狀態預報向量|k-1及其協方差矩陣|k-1；基于式（25）、式（26）計算DFIG機端電流虛擬量測。

3）機端電氣量估計：利用式（27）、式（28）構造冗余量測集；基于式（29）～式（32）對擾動和不良數據進行判別，并根據判定結果確定量測集各元素的權重；利用式（33）～式（35）估計所有DFIG機端電氣量。

5）令=+1，返回步驟2），進行下一次迭代。

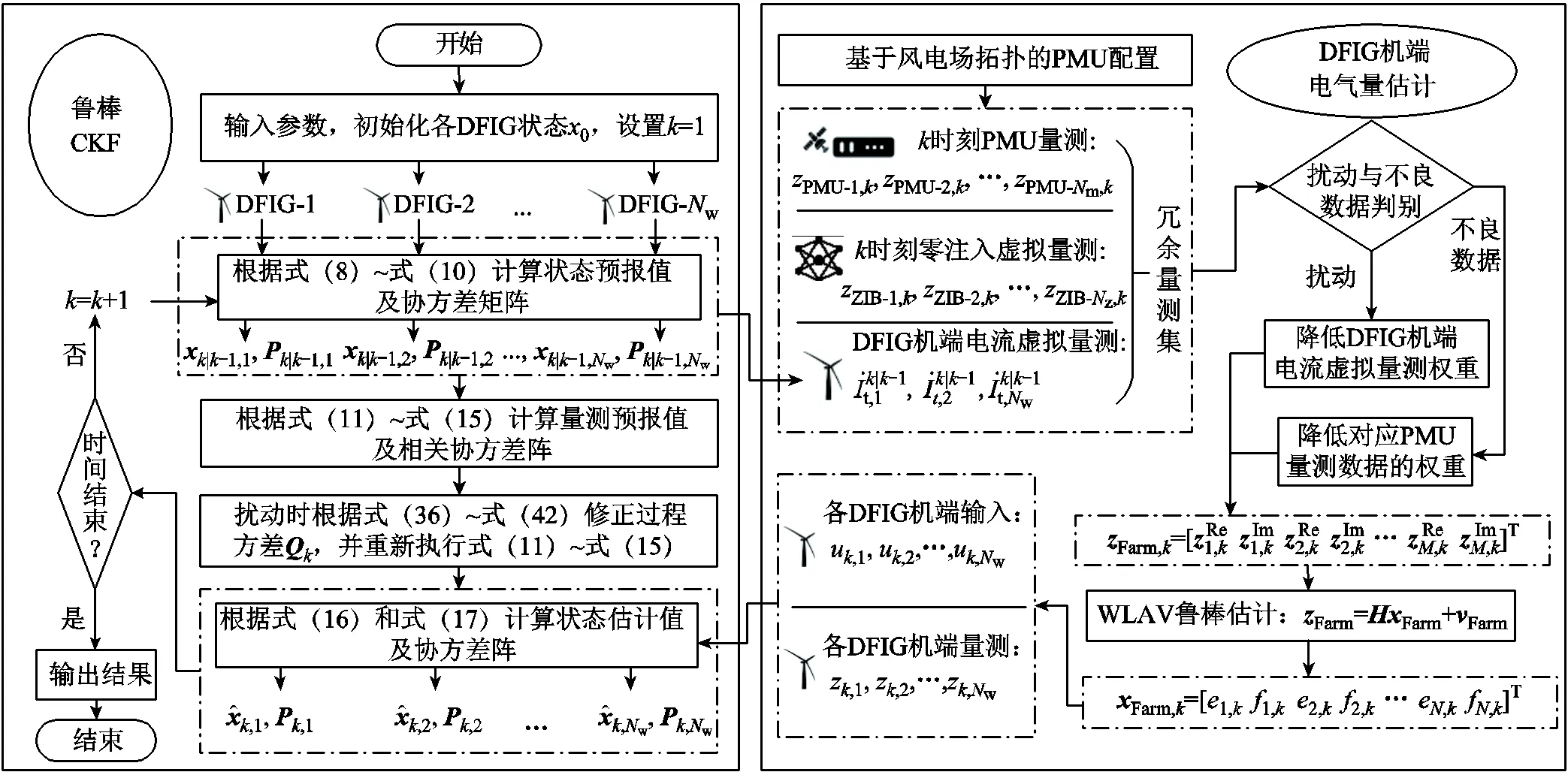
圖3 本文所提方法流程

5 算例分析

5.1 算例1：含16臺DFIG風電場

5.1.1 量測布點及仿真設置

在Matlab/Simulink中構建了如圖4a所示的風電場，DFIG使用Simulink內置的相量模型，采用一機組一箱變的接線方式，16臺1.5MW雙饋風機通過4條集電線路連接至風電場主變壓器，DFIG和風電場的具體參數見附表1。

按照2.1節量測配置方法，輸入上述風電場的拓撲信息，生成節點關聯矩陣，并按以下步驟求解。

1）輸入目標函數系數矩陣1。

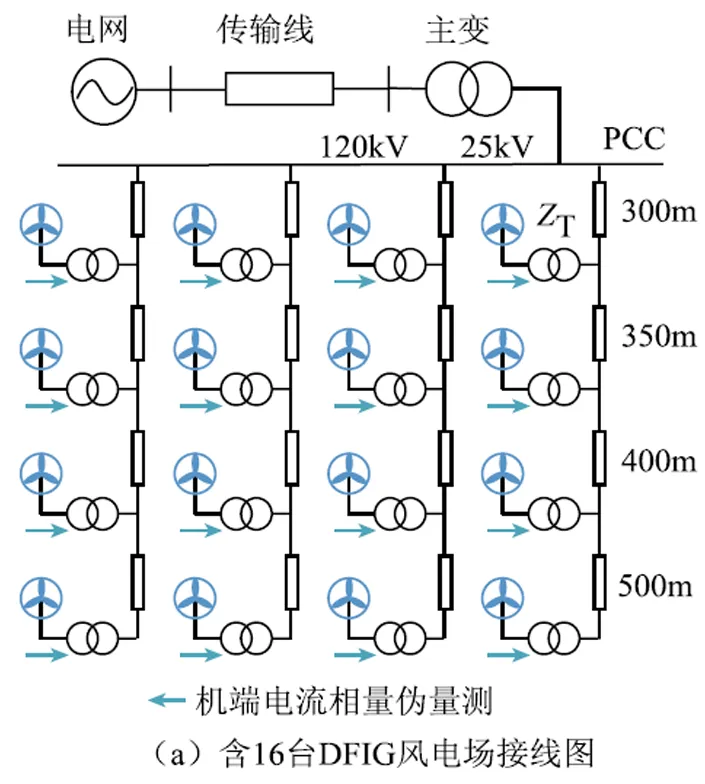
表1 算例1中PMU布點方案詳細信息

Tab.1 Detailed information of PMU placements in case 1

2）根據零注入節點約束和葉子節點約束，設置相關不等式約束ineq≤ineq、等式約束eq=eq中的系數矩陣ineq、eq和約束向量ineq、eq。

3）各元素取0或1，故上限b=1、下限b=0。

4）利用Matlab中intlinprog函數求解，[, min1()] = intlinprog(1,ineq,ineq,eq,eq,b,b)。

所得PMU配置方案如圖4b所示，詳細信息見表1。以最左側集電線路為例，在節點6安裝PMU，可使節點4、5、8可觀測，由于流過支路8-6的電流等于支路7-8的電流，故節點7也可觀測；在節點33安裝PMU，可使節點2可觀測，由于節點2、4為零注入節點，由零注入節點約束可知節點1、3也可觀測，故這一條集電線路的節點都可觀，其他集電線路的分析類似。由上述分析可知，由于考慮了風電場內節點間的電氣聯系，在該風電場每條集電線路配置1臺PMU即可實現該風電場內所有節點可觀測。結合2.2節基于DFIG動態模型所得到的機端電流相量虛擬量測，如圖4a中（藍色）箭頭所示，即可得到用于估計風場內所有DFIG機端電氣量的冗余量測集合。

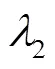
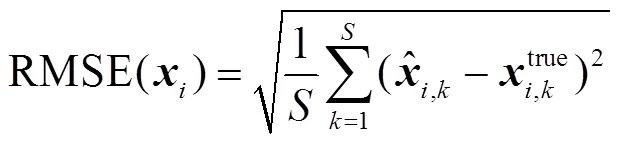
式中，為總的采樣點個數；為時刻第個狀態的估計值；true為時刻第個狀態的真值。

5.1.2 DFIG機端電氣量的估計準確性評價

基于風電場時空維度信息和WLAV來估計所有DFIG的機端電氣量，能夠降低量測需求并濾除不良數據，本節對此進行仿真驗證。

1）量測正常

在正常量測情況下，設置不同幅度的電壓降落和量測噪聲，測試突變檢測的準確性。三相短路的過渡電阻分別設置為1Ω和5Ω，對應風場并網點（Point of Common Coupling, PCC）電壓幅值分別跌落65%和15%，并分別添加1%和0.1%的量測噪聲，檢測結果如圖5所示。

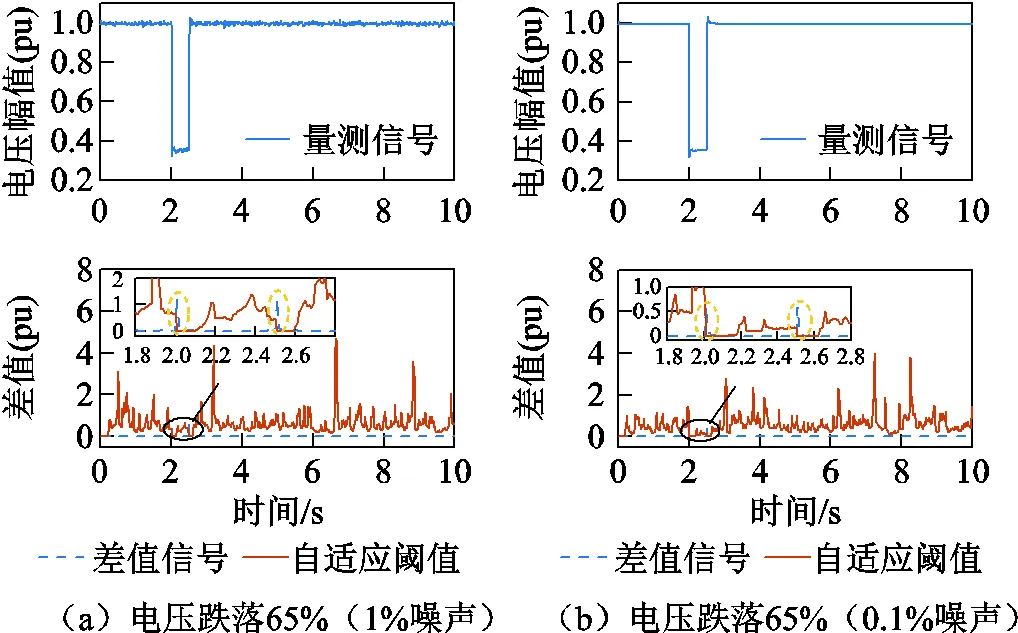
由圖5可知，對于不同幅度電壓降落和噪聲的影響，正常運行時差值信號在閾值以下，發生擾動時差值信號的方差變大，閾值能夠自適應減小，而差值信號則會上升并超過閾值，即能夠準確檢測到擾動導致的突變，且對不同情況的適應性較強。

在上述情況下，風電場內的PMU均檢測到突變，因此判定有擾動，故降低所有DFIG機端電流虛擬量測在機端電氣量估計中的權重。PCC電壓跌落65%時，節點3所連接DFIG的機端電流虛擬量測和估計值如圖6所示，該節點未安裝PMU。由于擾動無法預測，擾動發生后DFIG機端電流預報值存在偏差；通過增大其對應的量測方差后，估計值更傾向于風電場內的PMU量測值，因此能夠準確跟蹤實際值的變化。

為驗證DFIG機端電流虛擬量測對提高估計結果精度的有效性，設置三組量測集：5.1.1節配置方案中PMU測得的電壓電流相量構成量測集1；量測集1和所有DFIG機端電流虛擬量測構成量測集2；假設所有DFIG機端都安裝PMU這一理想情況，其測得的電壓電流相量構成量測集3。圖7比較了這三組量測集下節點3電壓的估計結果，可知量測集1的估計結果雖能跟蹤電壓變化趨勢，但存在較大誤差，這是由于5.1.1節的量測配置方案只保證系統可觀，但量測冗余度低；量測集2的估計結果誤差與量測集3接近，說明利用DFIG機端電流虛擬量測確實可以提高估計結果精度。

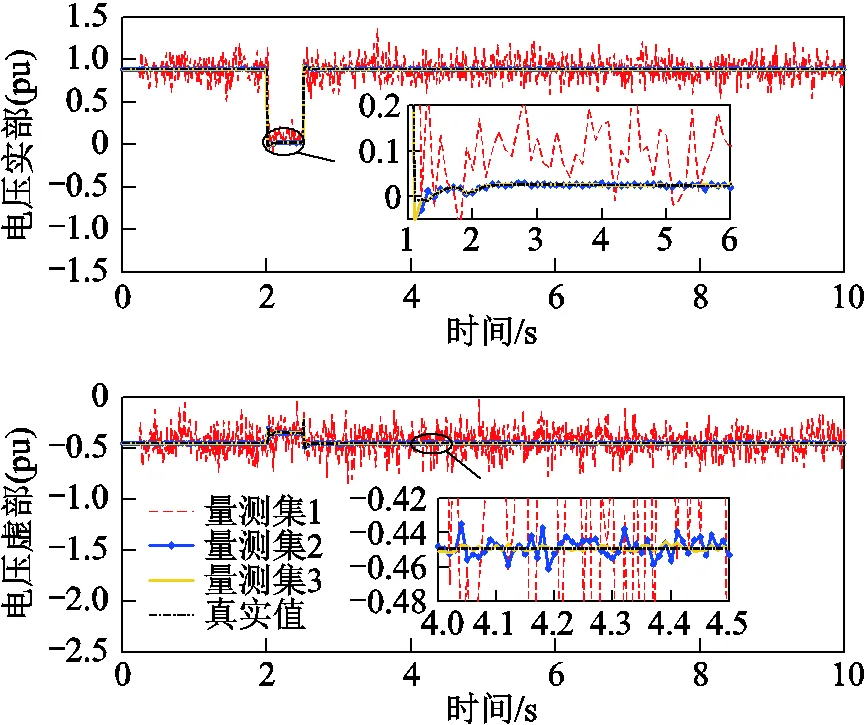
圖7 節點3電壓估計值的比較

表2 不同量測集估計結果RMSE的比較

Tab.2 Comparison of RMSE of different measurement sets

2）量測存在不良數據

在PCC電壓幅值跌落65%時，4.0～4.3s在安裝有PMU的節點6電壓量測幅值中加入10%的隨機不良數據。PCC和節點6的電壓量測幅值及突變檢測結果如圖8所示，可以看出，在2.0s和2.5s時，PCC和節點6電壓幅值的差值信號上升，自適應閾值下降，即都檢測到了突變；在4.0～4.3s時，系統不存在擾動，圖8a中PCC電壓幅值的差值信號遠小于自適應閾值，而節點6的電壓幅值存在不良數據，導致圖8b中的差值信號超過了閾值，即檢測到突變。所有PMU的檢測結果見表3，“√”表示檢測到突變，可知在2.0s和2.5s時所有PMU都檢測到了擾動，因此判定擾動發生；而在4.0～4.3s只有節點6的PMU檢測到擾動，因此判定其存在量測不良數據，進而減小其量測數據的權重。

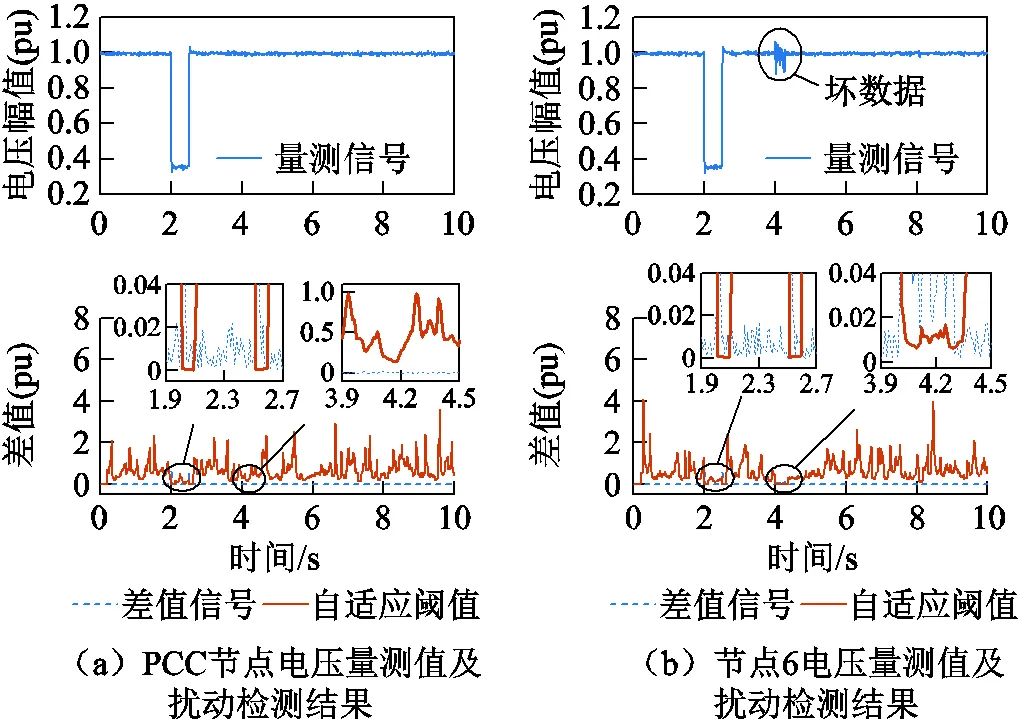
圖8 PCC和節點6的突變檢測結果

表3 擾動與不良數據判別結果

Tab.3 Judgement results of disturbance and bad data

在節點6電壓量測幅值存在不良數據時，節點6和節點3的電壓相量實部估計值如圖9所示，為了突出WLAV對量測不良數據的魯棒性，選擇WLS作為對比。可以看出，對于安裝了PMU的節點6，WLAV和WLS能夠有效降低PMU的量測誤差；在擾動或量測存在不良數據時，WLAV的估計值依然準確；而WLS的估計結果誤差相比量測值小，但仍大于WLAV。對于未安裝PMU的節點3，其節點電壓實部的WLS估計結果受擾動和節點6 的PMU不良數據的影響，而WLAV的估計結果較準確，表現出了較強的魯棒性。

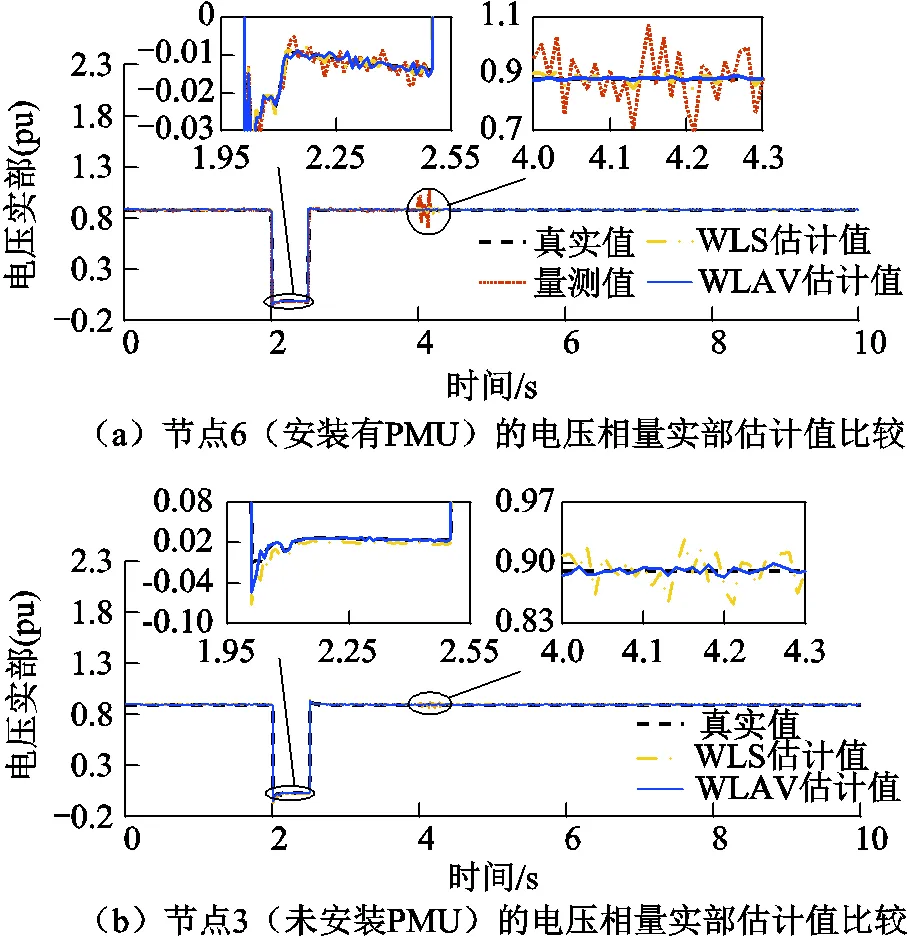
圖9 量測存在不良數據時節點6和節點3的電壓估計結果

5.1.3 DFIG魯棒動態狀態估計的準確性評價

本文所提方法通過DFIG機端電氣量魯棒估計，濾除輸入向量和量測向量中的不良數據，進而引入過程噪聲尺度因子抑制擾動影響，故該方法對輸入和量測不良數據及擾動同時具有魯棒性。本節通過仿真測試其對DFIG動態狀態估計的準確性，并選擇經典CKF作為對比算法1。文獻[14]中只基于新息處理量測不良數據的魯棒CKF作為對比算法2，文獻[25]中基于噪聲估值器的濾波算法作為對比算法3。

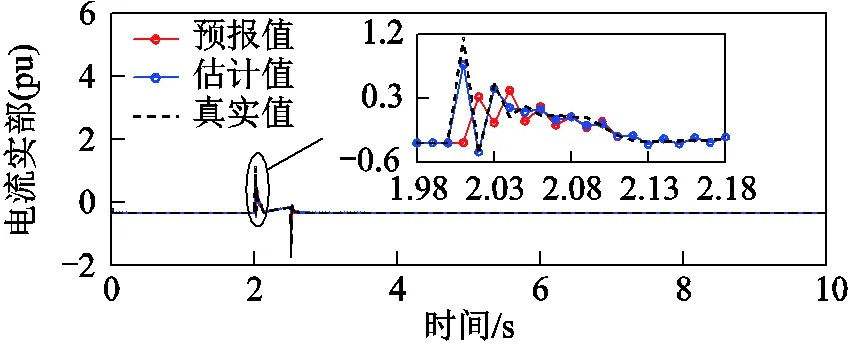
以節點5所連接的DFIG為研究對象，在2.0～2.5s設置三相短路故障，PCC電壓幅值跌落65%；在4.0～4.2s對式（7）量測向量中的輸出有功功率t加入10%的隨機不良數據；在6.0～6.2s對式（7）量測向量中的輸出有功功率t及輸入向量的節點電壓幅值都加入10%的隨機不良數據，四種方法部分狀態的估計結果如圖10所示。由圖10可知，在2.0 s發生故障時，由于本文算法基于過程噪聲尺度因子修正過程噪聲，估計結果較準確；而其他對比方法的估計值存在一定偏差，其中對比算法1和2本身不對擾動時不準確的預報值做處理，而對比算法3對的估計值在下一時刻才起作用，導致時刻預報值|k1的誤差協方差矩陣與實際不匹配，因此無法處理擾動時狀態的大幅變化。在4.0～4.2s只有量測存在不良數據時，本文算法和對比算法2能夠濾除量測不良數據的影響，而CKF和對比算法3的估計結果誤差較大；在6.0～6.2s，由于量測與輸入同時存在不良數據，只有本文算法能夠基于DFIG機端電氣量魯棒估計同時處理這兩種不良數據，估計結果與真實值基本吻合，其他三種方法的估計結果都出現了較大誤差。其中，對比算法2利用新息的異常來檢測并抑制不良數據，但無法處理輸入和量測同時存在不良數據的情況。

圖10 不同方法ωr、ψds與ψqs的估計結果對比

圖11對比了四種方法狀態估計值的RMSE。由于控制器中間變量1～7無實際物理意義，只統計了前8個狀態的RMSE，可知本文所提算法的RMSE最小，表明該方法能夠有效處理擾動的影響，并且輸入和量測都存在不良數據時，也具有較高的魯棒性。

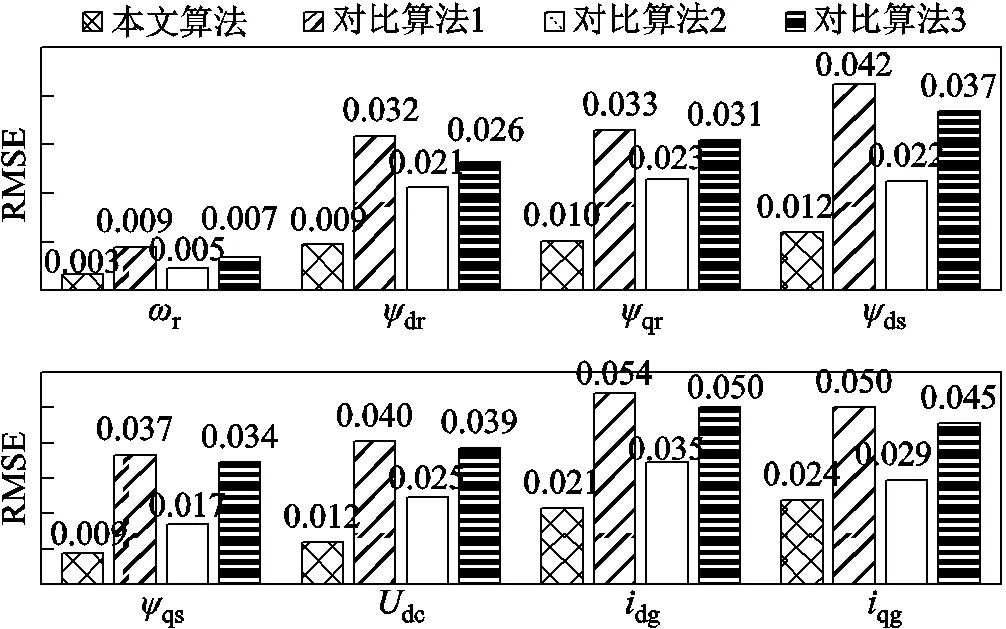
圖11 DFIG狀態估計結果的RMSE比較

此外，經多次測試后取平均，四種方法的單步計算時間見表4。由于考慮了風電場內的量測相關性，本文所提算法計算效率低于其他方法，但仍然能夠滿足實時性需求（PMU數據間隔10ms）。

表4 單步計算時間比較

Tab.4 Comparison of single step computation time

5.2 算例2：某實際風電場

為測試本文所提方法的適用性，以某實際風場[26]為研究對象進行算例分析。該算例中包含了兩個相同的風場，以模擬多風場協調的實際場景。每個風場中，32臺1.5MW雙饋風機通過集電線路連接至風電場主變，如圖12a所示。

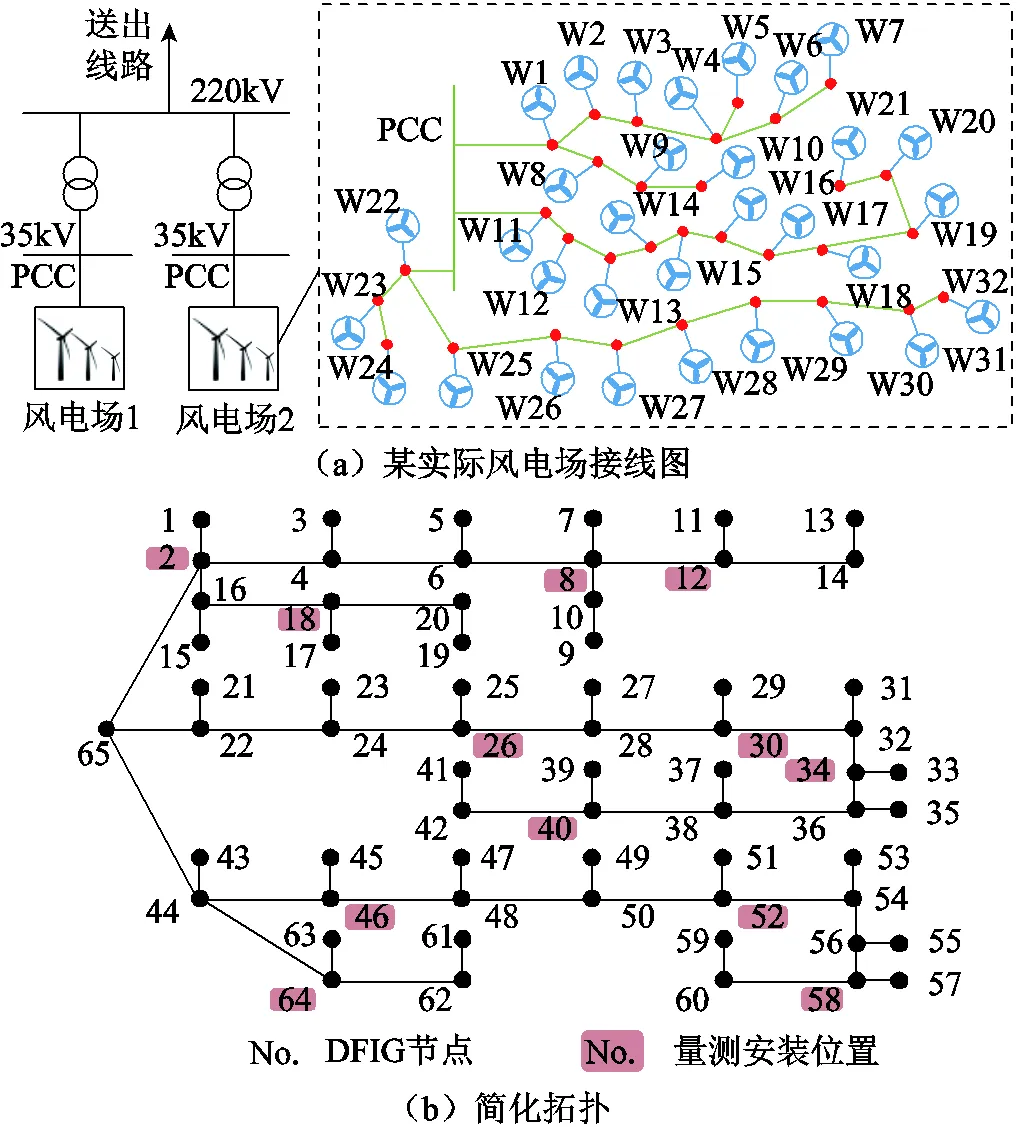
圖12 某實際風電場拓撲和量測配置

按照5.1.1節的PMU優化配置步驟，得到風電場2的布點方案如圖12b和表5所示，風電場1的配置與風電場2相同。可知，對于有32臺DFIG和65個節點的風電場，用12臺PMU可實現所有節點可觀測。

表5 算例2中PMU布點方案詳細信息

Tab.5 Detailed information of PMU placements in case 2

仿真開始時系統運行在穩定狀態，2s時220kV側發生三相短路故障，PCC電壓幅值跌落65%，500ms后故障清除，仿真時間持續10 s，采樣間隔0.01s，其他參數設置與算例1相同。設置與5.1.2節相同的三組量測集，其對應的風電場所有DFIG機端電壓和電流相量估計結果的RMSE均值見表6。可知，本文所提方法對應的量測集2的RMSE較小，且與理想量測集3接近。因此，在較大規模風電場中，將DFIG機端電流預報值作為虛擬量測同樣能夠有效提高量測冗余，并提高機端電氣量估計準確性。

表6 不同量測集估計結果RMSE的比較

Tab.6 Comparison of RMSE of different measurement sets

利用冗余量測集估計得到所有DFIG機端電氣量后，即可對單臺DFIG狀態進行估計。上述場景下，所有DFIG狀態的RMSE均值見表7，可知整體估計結果的平均誤差較小，證明所提方法在較大規模風場以及多風場協調場景下也具有較好的適用性。

表7 所有DFIG狀態估計結果的RMSE均值

Tab.7 Mean RMSE of all DFIGs

進一步地，以風電場2中的雙饋風機W1為研究對象，對有功功率t和節點電壓幅值的量測值分別加入不良數據，以模擬量測和輸入不良數據，具體參數與5.1.3節相同。然后，利用5.1.3節四種方法對風機W1的狀態進行估計，估計結果的RMSE見表8。可知，本文所提方法對應的RMSE最小，即在實際風電場算例中，該方法也具有較好的魯棒性。

表8 不同方法風機W1狀態估計結果的RMSE

Tab.8 Comparison of RMSE of W1 with different methods

6 結論

為克服風電場量測不足及DSE易受不良數據和擾動影響的問題，本文提出一種考慮風電場量測相關性的DFIG魯棒動態狀態估計方法，并通過仿真算例驗證了該方法的有效性，得出以下結論：

1）風電場可視為一個小型輻射狀電網，利用PMU最優配置及量測空間相關性可實現所有節點可觀，進而利用DFIG狀態的時間相關性可在量測不冗余時構造冗余量測集。對于仿真中有16臺和32臺DFIG的風電場，分別需要5臺和12臺PMU就可實現對所有節點狀態的準確估計。

2）在冗余量測集的基礎上，利用PMU量測的空間相關性可有效區分擾動和不良數據，并通過WLAV魯棒方法來估計所有DFIG的機端電氣量。仿真結果表明其能在DSE之前濾除PMU量測不良數據對輸入向量及量測向量的影響，解決了難以在DSE執行過程中對二者進行區分的問題。

3）針對擾動發生時DFIG狀態預報值不準確的問題，引入過程噪聲尺度因子，在擾動時降低預報值權重。仿真結果表明其能有效提高擾動時CKF估計結果的準確性。

附 錄

1. DFIG轉子側和網側變流器及其控制系統

由于變流器的時間常數是秒級，忽略其調制過程，即變流控制器輸出的參考電壓直接作為異步電機的勵磁電壓和換流器網側電壓，其控制框圖如附圖1所示。

正文中的1～7表示換流器控制框圖中7個PI環節的積分狀態變量，用i1～i7表示積分系數，p1～p7表示比例系數。

附圖1 換流器控制框圖

App.Fig.1 Converter control block diagram

積分環節的具體表達式為

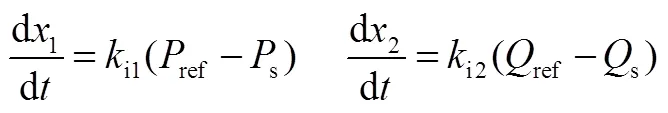
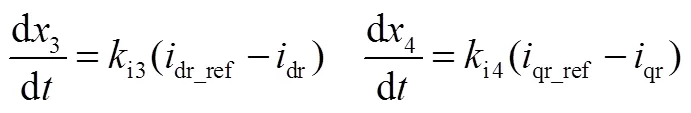
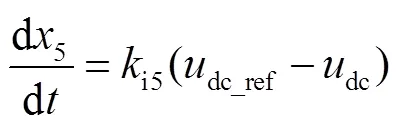
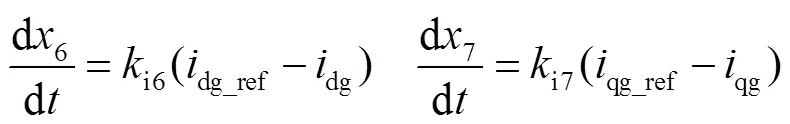
2. DFIG和風電場參數

附表1 DFIG和風電場參數

App.Tab.1 The parameters of DFIG and wind farm

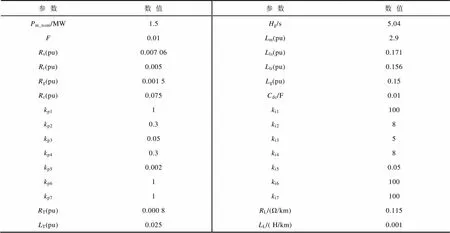
參數數值參數數值 Pm_nom/MW1.5Hg/s5.04 F0.01Lm(pu)2.9 Rs(pu)0.007 06Lls(pu)0.171 Rr(pu)0.005Llr(pu)0.156 Rg(pu)0.001 5Lg(pu)0.15 Rc(pu)0.075Cdc/F0.01 kp11ki1100 kp20.3ki28 kp30.05ki35 kp40.3ki48 kp50.002ki50.05 kp61ki6100 kp71ki7100 RT(pu)0.000 8RL/(Ω/km)0.115 LT(pu)0.025LL/( H/km)0.001

[1] 周博, 艾小猛, 方家琨, 等. 計及超分辨率風電出力不確定性的連續時間魯棒機組組合[J]. 電工技術學報, 2021, 36(7): 1456-1467.

Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.

[2] 陳昌松, 段善旭, 殷進軍, 等. 基于發電預測的分布式發電能量管理系統[J]. 電工技術學報, 2010, 25(3): 150-156.

Chen Changsong, Duan Shanxu, Yin Jinjun, et al. Energy management system of distributed generation based on power forecasting[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 150-156.

[3] Zhao Junbo, Gómez-Expósito A, Netto M, et al. Power system dynamic state estimation: motivations, definitions, methodologies, and future work[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3188-3198.

[4] 賈寧, 王彬, 孫宏斌, 等. 基于全景精細化模型的風電場能量管理系統研制及應用[J]. 電力系統保護與控制, 2016, 44(14): 61-68.

Jia Ning, Wang Bin, Sun Hongbin, et al. Development and application of panoramic fine modeling based wind farm energy management system[J]. Power System Protection and Control, 2016, 44(14): 61-68.

[5] 王彤, 高明陽, 黃世樓, 等. 基于自適應容積卡爾曼濾波的雙饋風力發電機動態狀態估計[J]. 電網技術, 2021, 45(5): 1837-1845.

Wang Tong, Gao Mingyang, Huang Shilou, et al. Dynamic state estimation for doubly fed induction generator wind turbine based on adaptive cubature Kalman filter[J]. Power System Technology, 2021, 45(5): 1837-1845.

[6] Yu Shenglong, Fernando T, Iu H H C, et al. Realization of state-estimation-based DFIG wind turbine control design in hybrid power systems using stochastic filtering approaches[J]. IEEE Transactions on Industrial Informatics, 2016, 12(3): 1084-1092.

[7] Yu Shenglong, Emami K, Fernando T, et al. State estimation of doubly fed induction generator wind turbine in complex power systems[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4935-4944.

[8] Liu Hao, Bi Tianshu, Xu Sudi, et al. A full-view synchronized measurement system for the renewables, controls, loads, and waveforms of power-electronics-enabled power distribution grids[J]. IEEE Transactions on Smart Grid, 2022, 13(5): 3879-3890.

[9] 巫春玲, 胡雯博, 孟錦豪, 等. 基于最大相關熵擴展卡爾曼濾波算法的鋰離子電池荷電狀態估計[J]. 電工技術學報, 2021, 36(24): 5165-5175.

Wu Chunling, Hu Wenbo, Meng Jinhao, et al. State of charge estimation of lithium-ion batteries based on maximum correlation-entropy criterion extended Kalman filtering algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5165-5175.

[10] Anagnostou G, Kunjumuhammed L P, Pal B C. Dynamic state estimation for wind turbine models with unknown wind velocity[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3879-3890.

[11] 焦自權, 范興明, 張鑫, 等. 基于改進粒子濾波算法的鋰離子電池狀態跟蹤與剩余使用壽命預測方法[J]. 電工技術學報, 2020, 35(18): 3979-3993.

Jiao Ziquan, Fan Xingming, Zhang Xin, et al. State tracking and remaining useful life predictive method of Li-ion battery based on improved particle filter algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3979-3993.

[12] 馬安安, 江全元, 熊鴻韜, 等. 考慮量測壞數據的發電機動態狀態估計方法[J]. 電力系統自動化, 2017, 41(14): 140-146.

Ma Anan, Jiang Quanyuan, Xiong Hongtao, et al. Dynamic state estimation method for generator considering measurement of bad data[J]. Automation of Electric Power Systems, 2017, 41(14): 140-146.

[13] 畢天姝, 陳亮, 薛安成, 等. 基于魯棒容積卡爾曼濾波器的發電機動態狀態估計[J]. 電工技術學報, 2016, 31(4): 163-169.

Bi Tianshu, Chen Liang, Xue Ancheng, et al. Dynamic state estimator for synchronous machines based on robust cubature Kalman filter[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 163-169.

[14] 劉朋成, 項中明, 江全元, 等. 基于魯棒容積卡爾曼濾波的同步發電機實時動態狀態估計方法[J]. 電網技術, 2019, 43(8): 2860-2868.

Liu Pengcheng, Xiang Zhongming, Jiang Quanyuan, et al. Real-time dynamic state estimation for synchronous machines based on robust CKF[J]. Power System Technology, 2019, 43(8): 2860-2868.

[15] 魏博, 邵沖, 張柏林, 等. 基于下垂特性的風電場參與電網快速頻率調整實測分析[J]. 電氣技術, 2020, 21(6): 39-44, 62.

Wei Bo, Shao Chong, Zhang Bolin, et al. Actual measurement and analysis of wind power plant participating in power grid fast frequency regulation base on droop characteristic[J]. Electrical Engineering, 2020, 21(6): 39-44, 62.

[16] Simon D. Optimal state estimation[M]. Hoboken: Wiley, 2006.

[17] 李龍源, 付瑞清, 呂曉琴, 等. 接入弱電網的同型機直驅風電場單機等值建模[J]. 電工技術學報，2022: 1-14．

Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs [J]. Transactions of China Electrotechnical Society, 2022: 1-14.

[18] Chen Xuebing, Wei Feng, Cao Shuyu, et al. PMU placement for measurement redundancy distribution considering zero injection bus and contingencies[J]. IEEE Systems Journal, 2020, 14(4): 5396-5406.

[19] Ghosh S, Isbeih Y J, Azman S K, et al. Optimal PMU allocation strategy for completely observable networkswith enhanced transient stability characteristics[J]. IEEETransactions on Power Delivery, 2022, 37(5): 4086-4102.

[20] 劉灝, 朱世佳, 畢天姝. 基于局部離群因子的PMU連續壞數據檢測方法[J]. 電力系統自動化, 2022, 46(1): 25-32.

Liu Hao, Zhu Shijia, Bi Tianshu. Continuous bad data detection method for PMU based on local outlier factor[J]. Automation of Electric Power Systems, 2022, 46(1): 25-32.

[21] 楊曉梅, 羅月婉, 肖先勇, 等. 基于自適應閾值和奇異值分解的電能質量擾動檢測新方法[J]. 電網技術, 2018, 42(7): 2286-2294.

Yang Xiaomei, Luo Yuewan, Xiao Xianyong, et al. A new detection approach of power quality disturbances based on adaptive threshold and singular value decomposition[J]. Power System Technology, 2018, 42(7): 2286-2294.

[22] Rouhani A, Abur A. Linear phasor estimator assisted dynamic state estimation[J]. IEEE Transactions on Smart Grid, 2018, 9(1): 211-219.

[23] 國家質量監督檢驗檢疫總局, 中國國家標準化管理委員會. GB/T 26862—2011 電力系統同步相量測量裝置檢測規范[S]. 北京: 中國標準出版社, 2011.

[24] 國家電網公司. Q/GDW 11491-2015 風電機組建模驗證及參數校驗導則[S]. 北京，2016.

[25] 趙洪山, 田甜. 基于自適應無跡卡爾曼濾波的電力系統動態狀態估計[J]. 電網技術, 2014, 38(1): 188-192.

Zhao Hongshan, Tian Tian. Dynamic state estimation for power system based on an adaptive unscented Kalman filter[J]. Power System Technology, 2014, 38(1): 188-192.

[26] 韓佶, 苗世洪, 李力行, 等. 基于多視角遷移學習的風場內機群劃分及等值風場參數綜合優化[J]. 中國電機工程學報, 2020, 40(15): 4866-4881.

Han Ji, Miao Shihong, Li Lixing, et al. Wind turbines clustering in wind farm based on multi-view transfer learning and synthetic optimization of parameters in equivalent wind farm[J]. Proceedings of the CSEE, 2020, 40(15): 4866-4881.

Robust Dynamic State Estimation of Doubly-Fed Induction Generator Considering Measurement Correlation in Wind Farms

Zhu Maolin Liu Hao Bi Tianshu

（State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Beijing 102206 China）

Wind power is characterized by strong intermittency, random fluctuating and low schedulability. Dynamic state estimation (DSE) of doubly-fed induction generators (DFIGs) based on phasor measurement unit (PMU) can provide reliable data basis for wind farm energy management system, which helps to suppress the influence of wind power fluctuation on power grid. However, DSE of a single DFIG needs input its terminal measurements, but currently it is not common for wind farms (WFs) configuring PMUs for each wind turbine. Besides, DSE based on the prediction-filtering framework of Kalman filter is susceptible to bad measurement data and disturbances. To address these issues, this paper proposes a robust DSE method of DFIG considering the measurement correlation in WFs.

Firstly, considering that a WF can be considered as a small radial grid, its topological characteristics are leveraged to obtain the optimal installation locations of PMUs. And the time-dimension constraint information of DFIG dynamic model is included to construct the redundant measurement set. Secondly, the terminal electrical quantities of all DFIGs are estimated by weighted least absolute value (WLAV) estimation method based on the redundant measurement set. This way, the bad data in the DSE inputs and measurements can be filtered out by WLAV after distinguishing disturbances and bad measurement data. Finally, when the innovation of cubature Kalman filter is abnormal, it can be considered that the prediction vector deviates from the true value. The process noise covariance matrix is then adjusted by introducing a process noise scale factor, which can reduce the influence of the predicted values on the final estimation results. Thus, this integrated method has low requirements for measurement configuration and can deal with disturbances and bad data in the DSE inputs and measurements simultaneously.

Simulation results on a WF with 16 DFIGs show that, only 5 PMUs are needed to make all buses of the WF observable, and the dimension of the measurement set increases from 34 to 50 by incorporating the predicted terminal currents of all DFIGs as virtual measurements. As the measurement redundancy increases, the root-mean-square error (RMSE) of the estimated DFIG terminal electrical quantities reduces from 0.251 to 0.009 which is close to the RMSE of the ideal measurement set. Besides, based on the spatial correlation of the PMU measurements at the different buses, the voltage drop disturbance at the point of common coupling and bad measurement data at Bus 6 are correctly detected and discriminated. And when bad measurement data and disturbances exist, the mean RMSE of the dynamic states estimated by the proposed method is lower than other comparison methods. For example, the RMSE of rotor speed drops from 0.009 to 0.003. Simulation is also carried out on an actual wind farm in a certain area to verify the performance of the proposed method for large scale wind farms, and the results demonstrate its good generalization ability.

The following conclusions can be drawn from the simulation analysis: ① With the optimal configuration of PMUs and the spatial correlation of phasor measurements, all wind farm buses can be observed with a small number of PMUs. The temporal correlation of DFIG dynamic states can be leveraged to construct the redundant measurement to improve the estimation accuracy. ② The spatial correlation of PMU measurements can be used to effectively distinguish disturbances and bad measurement data. And the robust WLAV method is used to estimate the terminal electrical quantities of all DFIGs. It can also filter out the influence of PMU bad data on input vector and measurement vector of DSE, which is difficult to cope with during the DSE execution. ③The process noise scale factor introduced to reduce the weight of prediction value is able to deal with the inaccurate predicted states of DFIG when a disturbance occurs.

Doubly-fed induction generator, dynamic state estimation, measurement correlation, minimum absolute value, robust cubature Kalman filter

10.19595/j.cnki.1000-6753.tces.221468

TM614

國家自然科學基金資助項目（51725702）。

2022-07-29

2022-10-12

朱茂林 男，1996年生，博士研究生，研究方向為電力系統動態狀態估計。E-mail：mlzhu@ncepu.edu.cn

劉 灝 男，1985年生，副教授，研究方向為廣域同步相量測量技術。E-mail：hliu@ncepu.edu.cn（通信作者）

（編輯 赫蕾）