飛行器翼型表面流場數(shù)據(jù)智能分區(qū)*

胡躍迪,蘇 想,李 楠,張麗梅

(北京工商大學(xué)人工智能學(xué)院，北京 100048)

1 引言

隨著復(fù)雜裝備先進設(shè)計制造手段的進步與發(fā)展，計算流體力學(xué)CFD(Computational Fluid Dynamics)的應(yīng)用越來越廣泛[1]，目前，借助高性能計算機系統(tǒng)，可以計算、存儲規(guī)模巨大且復(fù)雜度較高的CFD流場數(shù)據(jù)[2]。由于設(shè)計對象的復(fù)雜度增加，CFD仿真產(chǎn)生的流場數(shù)精度也在不斷提高，因此對流場數(shù)據(jù)的分析和處理也有越來越高的要求，這為流場數(shù)據(jù)后處理帶來了巨大的挑戰(zhàn)。

由于航空航天業(yè)的不斷發(fā)展，飛行器設(shè)計的復(fù)雜度不斷提高，使得飛行器設(shè)計的時間周期愈來越長。設(shè)計人員在飛行器的氣動外形設(shè)計和仿真過程中，往往需要根據(jù)仿真結(jié)果重點分析某一區(qū)域而不是整個氣動外形的各物理參數(shù)計算結(jié)果分布情況，并根據(jù)分析結(jié)果進行設(shè)計優(yōu)化。因此，根據(jù)仿真結(jié)果的多物理場分布自動化地進行區(qū)域劃分，找出技術(shù)人員需要重點關(guān)注的一個或幾個區(qū)域，使設(shè)計師可以對特定的某些流場區(qū)域進行更精細的計算，可以在相當(dāng)程度上提升設(shè)計分析迭代過程的自動化程度，進而提升設(shè)計的效率和質(zhì)量。

Figure 1 Overall technology roadmap圖1 總技術(shù)路線圖

在國內(nèi)，針對流場數(shù)據(jù)后處理可視化的研究已產(chǎn)生了不少系統(tǒng)級成果，如國家數(shù)值風(fēng)洞項目的 NNW-TopViz(National Numerical Windtunnel-TopViz)流場可視分析系統(tǒng)[3]等。

在基本的流場數(shù)據(jù)可視化基礎(chǔ)上，常常還需要針對后處理數(shù)據(jù)進行進一步分析和處理。Str?fer等[4]利用循環(huán)神經(jīng)網(wǎng)絡(luò)識別翼體連接處三維流動中的馬蹄渦，將深度神經(jīng)網(wǎng)絡(luò)應(yīng)用在三維流場中。Franz等[5]將卷積神經(jīng)網(wǎng)絡(luò)的特征學(xué)習(xí)與已有的圖像處理工具特征跟蹤器相結(jié)合，提出了一個基于深度學(xué)習(xí)的渦檢測和跟蹤框架。針對現(xiàn)有機器學(xué)習(xí)方法在旋渦提取中存在的訓(xùn)練集本身并不完全準(zhǔn)確和準(zhǔn)確率評價不夠嚴謹?shù)膯栴}，提出了基于全卷積分割網(wǎng)絡(luò)的旋渦提取方法，用于檢測流場數(shù)據(jù)中的旋渦結(jié)構(gòu)。

還有研究人員利用語義分割[6,7]等方法對仿真結(jié)果進行后處理。姚葉等[8]提出了基于深度學(xué)習(xí)的流場數(shù)據(jù)后處理方法，將可視化和對流場數(shù)據(jù)后處理的機器學(xué)習(xí)方法結(jié)合起來，將三維的流場數(shù)據(jù)轉(zhuǎn)化為二維的流場圖像，再對二維流場圖像進行智能分區(qū)，分區(qū)速度得到了有效的提升。但是，由于在降維的過程中直接舍棄了一個維度的數(shù)據(jù)，使得新得到的二維流場圖像與原三維流場數(shù)據(jù)相差較大，所以得到的分區(qū)結(jié)果的正確率也不理想。

根據(jù)以上研究，本文針對機翼翼型這一類特定問題，提出了基于參數(shù)化算法的流場結(jié)果數(shù)據(jù)降維并智能分區(qū)的方法。該方法總體技術(shù)思路如圖1所示，包含如下4部分：

(1)樣本數(shù)據(jù)集生成：采用參數(shù)化批量機翼翼型建模和網(wǎng)格生成技術(shù)批量生成待求解網(wǎng)格，再利用CFD數(shù)值模擬來批量生成流場數(shù)據(jù)。

(2)將流場數(shù)據(jù)重采樣并矩陣化：基于參數(shù)化算法將3維流場數(shù)據(jù)映射到二維平面，再把平面三角網(wǎng)格流場數(shù)據(jù)重采樣為矩陣數(shù)據(jù)。

(3)設(shè)計并構(gòu)建卷積神經(jīng)網(wǎng)絡(luò)模型，針對流場數(shù)據(jù)分區(qū)任務(wù)進行訓(xùn)練。

(4)通過逆映射將矩陣數(shù)據(jù)重采樣到三維網(wǎng)格，使分區(qū)結(jié)果在原機翼模型上進行可視化展示。

2 參數(shù)化翼型流場數(shù)據(jù)批量計算

以往構(gòu)建流場數(shù)據(jù)集時，一般采用飛行試驗，使用真實飛機在真實場景下飛行得到流場數(shù)據(jù)。如此得到的流場數(shù)據(jù)清晰準(zhǔn)確，但耗時巨大。本文的數(shù)據(jù)集構(gòu)建采用CFD數(shù)值模擬完成。通過變化仿真前的處理參數(shù)，得到大量不同機翼外形的仿真流場數(shù)據(jù)。參數(shù)化數(shù)據(jù)驅(qū)動方式可以使數(shù)據(jù)集批量化自動生成，提升了數(shù)據(jù)集的構(gòu)建效率。

2.1 氣動外形參數(shù)化批量生成及數(shù)值模擬

為了批量生成大量的機翼流場數(shù)據(jù)以構(gòu)建數(shù)據(jù)集，需要使用CFD仿真軟件來進行流場數(shù)值模擬。數(shù)值模擬方法采用基于直角網(wǎng)格的解算器完成。流場數(shù)據(jù)的生成主要分為3個步驟：網(wǎng)格生成及計算參數(shù)設(shè)置；直角網(wǎng)格生成；流場計算。針對生成流場數(shù)據(jù)之前的模型問題，可以通過參數(shù)化驅(qū)動批量修改氣動外形來實現(xiàn)，如圖2所示：(1)定義機翼兩端面曲線種子點；(2)將種子點擬合成線；(3)通過放映方法將線組合成模型。生成不同的機翼模型后，設(shè)置好三角網(wǎng)格密度，然后對機翼模型進行數(shù)值計算，得到流場文件。

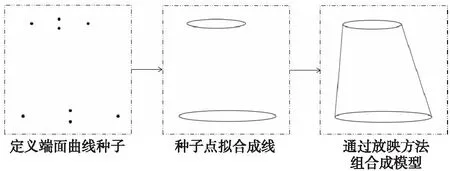
Figure 2 Parametric generation of wing airfoils圖2 參數(shù)化生成機翼翼型

2.2 基于參數(shù)化的表面三維流場數(shù)據(jù)降維

由于高維流場數(shù)據(jù)量大，所以直接對高維流場進行分區(qū)處理時，會使處理時間過長，從而影響效率。如果對高維流場進行降維和矩陣化處理，就可以縮短處理時間,提高效率。

為了更直觀、清晰地展示流場數(shù)據(jù)，更方便對流場數(shù)據(jù)進行后處理，需要提取流場數(shù)據(jù)中某些重要的數(shù)據(jù)。流場數(shù)據(jù)中比較重要的數(shù)據(jù)就是點(三維空間中的x、y、z軸方向的坐標(biāo))、單元(由坐標(biāo)點形成三角網(wǎng)格)和點上對應(yīng)的流場數(shù)據(jù)。所以，需要將這3種數(shù)據(jù)提取出來組成一個新的網(wǎng)格數(shù)據(jù)。為了使三維數(shù)據(jù)降維，需要對數(shù)據(jù)進行參數(shù)化，也就是對生成的網(wǎng)格數(shù)據(jù)進行表面參數(shù)化。通過表面參數(shù)化可以將一個立體幾何的3D頂點坐標(biāo)重新編碼成2D頂點坐標(biāo)。從紋理映射到表面重新網(wǎng)格化已經(jīng)提出了許多參數(shù)化算法。

目前，計算共形幾何在很多領(lǐng)域中得到了廣泛的應(yīng)用。計算共形幾何主要研究保角變換下的不變量和曲面之間的共形映射[9]。為了使得轉(zhuǎn)換后的數(shù)據(jù)與原數(shù)據(jù)盡量相同，需要用到共形映射(即保角變換下不變量)，保角映射局部上保持形狀(三角面片角度)不變。計算共形幾何中的調(diào)和映射主要用于計算虧格為零的封閉拓撲球面或者帶邊界的拓撲圓盤[10 - 12]。調(diào)和映射的基本原理是優(yōu)化調(diào)和能量，當(dāng)調(diào)和能量達到最小時，映射就是調(diào)和映射。輸入一個帶邊界的拓撲圓盤M:

(1)遍歷拓撲圓盤的邊界，存儲邊界點到鏈表，如式(1)所示：

?M={v0,v1,…,vn-1}

(1)

(2)計算整個邊界的長度，如式(2)所示；

(2)

其中，lvi,vi+1為2點[vi,vj]的長度。

(3)設(shè)置邊界條件，如式(3)～式(5)所示；

(3)

(4)

f(vi)=(cosθi,sinθi),vi∈?M

(5)

(4)使用牛頓迭代法優(yōu)化調(diào)和能量,如式(6)所示：

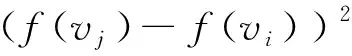
(6)

其中，kij表示調(diào)和能量[13]。

調(diào)和映射是一種固定邊界的參數(shù)化算法，算法高效且簡單，但相比不固定邊界的算法會產(chǎn)生較大的失真。

最小二乘保角參數(shù)化LSCM(Least Squares Conformal Maps parametrization)與調(diào)和映射不同，它不需要有固定的邊界,其中心思想是已知一組點的數(shù)據(jù)(x,y)，可以近似為線性關(guān)系y=ax+b，目標(biāo)為確定常數(shù)a和b，如式(7)所示；

(7)

找到a和b，使得所有yi與axi+b偏差的平方和Q最小。

ARAP(As-Rigid-As-Possible parametrization)是用于計算盡量保持距離(以及角度)的參數(shù)化：每個三角形都映射到試圖保持其原始形狀的平面，直至進行剛性旋轉(zhuǎn)，最后邊界可以自由變形，以最小化失真，可以做到保剛性(即保角又保形)。

ARAP變形算法的核心能量函數(shù)如式(8)所示，通過最小化該能量函數(shù)實現(xiàn)模型的盡可能剛性變形。Ai到Bi進行剛體變換，變換過程中存在旋轉(zhuǎn)矩陣Ri，如式(8)所示：

(8)

其中，Ai和Bi分別表示變形前后模型頂點ai和bi對應(yīng)的變形單元，N(i)表示ai的1-鄰域點的索引，aj和bj分別表示ai和bi的1-鄰域頂點，Ri表示Ai到Bi的最優(yōu)旋轉(zhuǎn)矩陣，Wij是邊eij=(ai,aj)的權(quán)重[14]。

圖3為三維模型經(jīng)過調(diào)和映射，LSCM和ARAP的三角網(wǎng)格角度和坐標(biāo)點距離變化圖。

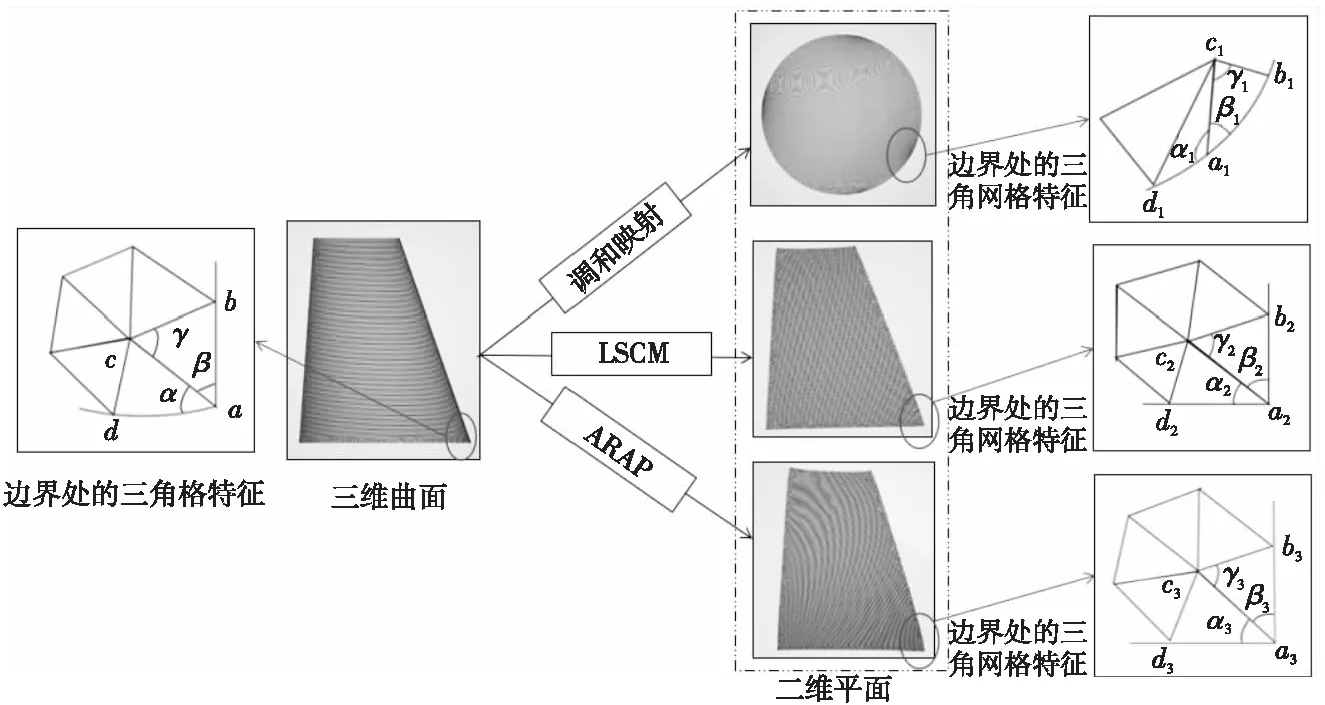
Figure 3 Changes before and after dimensionality reduction by different parameterization methods圖3 不同參數(shù)化方法降維前后的變化

坐標(biāo)點a，b，c和d經(jīng)過調(diào)和映射變?yōu)閍1，b1，c1和d1，經(jīng)過LSCM變?yōu)閍2，b2，c2和d2，經(jīng)過ARAP變?yōu)閍3，b3，c3和d3。從圖3中可以看出，三維模型經(jīng)過調(diào)和映射后邊界處坐標(biāo)點之間的疏密程度發(fā)生的變化大于經(jīng)過LSCM和ARAP發(fā)生的變化。將流場數(shù)據(jù)重采樣為矩陣數(shù)據(jù)是根據(jù)映射后的u和v坐標(biāo)點進行重采樣。為了使重采樣后的矩陣數(shù)據(jù)與原三維流場數(shù)據(jù)更相近，需要映射前后的坐標(biāo)點之間的距離變化最小，距離變化是流場數(shù)據(jù)矩陣化后前后相近程度的重要因素。

LSCM在映射的過程中盡可能地保持三角形的角度相同，ARAP算法在LSCM的基礎(chǔ)上盡可能地保證三角形沒有扭曲地映射在二維平面上。相比于LSCM，經(jīng)過ARAP的坐標(biāo)點與原三維坐標(biāo)更相近，所以只需要討論調(diào)和映射和ARAP對數(shù)據(jù)矩陣化的影響，如圖4所示。三維流場數(shù)據(jù)經(jīng)過調(diào)和映射后部分坐標(biāo)點之間的距離和角度變化較大，將映射后的二維網(wǎng)格數(shù)據(jù)矩陣化后，可以看出新的矩陣數(shù)據(jù)分區(qū)不均等；三維流場數(shù)據(jù)經(jīng)過ARAP后坐標(biāo)點之間的距離和角度變化較小，將映射后的二維網(wǎng)格數(shù)據(jù)矩陣化后，可以看出新的矩陣數(shù)據(jù)分區(qū)均等。

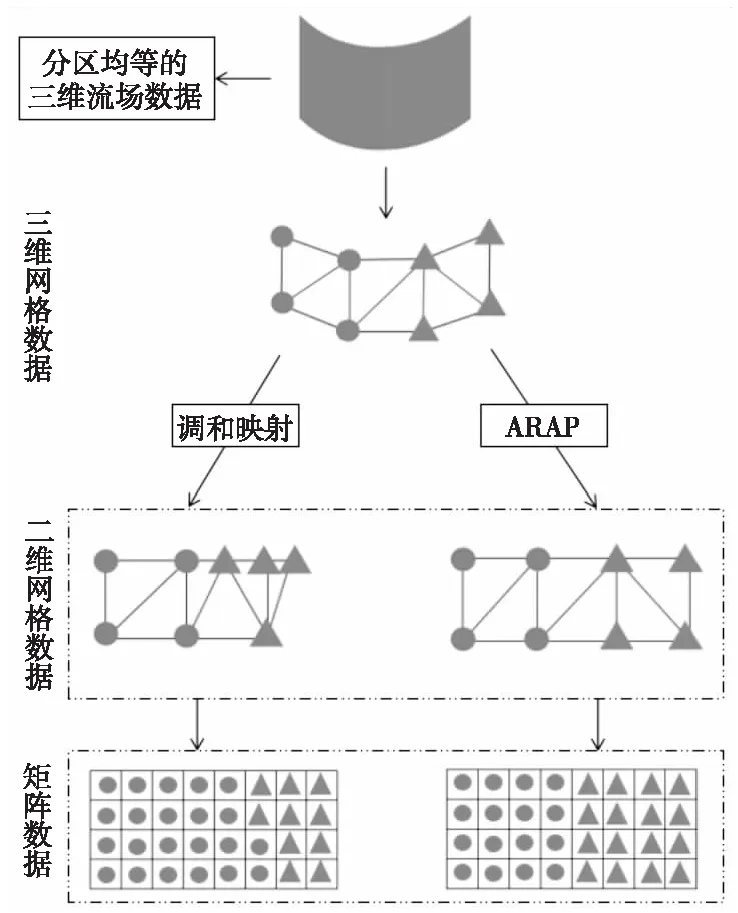
Figure 4 Matrixing with harmonic mapping and ARAP圖4 經(jīng)過調(diào)和映射和ARAP的矩陣化

3 非結(jié)構(gòu)化流場數(shù)據(jù)重采樣及矩陣化

由于智能分區(qū)模型的輸入需要的是結(jié)構(gòu)化的矩陣數(shù)據(jù)，所以要將非結(jié)構(gòu)化的網(wǎng)格數(shù)據(jù)重采樣為結(jié)構(gòu)化的矩陣數(shù)據(jù)。流場數(shù)據(jù)的結(jié)構(gòu)化處理可以在確保流場數(shù)據(jù)信息變化較小的情況下改變流場的結(jié)構(gòu)形式，使得新產(chǎn)生的流場數(shù)據(jù)可以作為智能分區(qū)模型的輸入。對于分析數(shù)據(jù)而言，非結(jié)構(gòu)化數(shù)據(jù)的分析工具目前還處于萌芽和發(fā)展階段，而對于結(jié)構(gòu)化數(shù)據(jù)已有成熟的分析工具，所以有必要將流場數(shù)據(jù)進行結(jié)構(gòu)化處理。

3.1 三角網(wǎng)格流場數(shù)據(jù)矩陣化方法

由于得到的流場數(shù)據(jù)分布在點上而不是單元上，所以先考慮點的位置和點對應(yīng)的流場數(shù)據(jù)。在矩陣化時，先重采樣點的位置，然后在重采樣后的格點上填上對應(yīng)的流場數(shù)據(jù)。

經(jīng)過降維后的三角網(wǎng)格數(shù)據(jù)可以看成一個平面(u,v)坐標(biāo)系上的點，將u，v坐標(biāo)上的點重采樣到三維矩陣AM×N×P上。先找到(u,v)坐標(biāo)系對應(yīng)的矩陣格點位置，如式(9)和式(10)所示：

(9)

(10)

其中，m，n分別為矩陣格點的行和列的位置；M，N分別為矩陣的行數(shù)和列數(shù),(x,y)為u,v坐標(biāo)系上的點。

圖5為矩陣化算法流程圖。圖6是三角網(wǎng)格數(shù)據(jù)矩陣化示意圖，最后得到的是重采樣后的三維矩陣可視化的效果。為了使數(shù)據(jù)矩陣化過程中的誤差最小，需要保證流場數(shù)據(jù)上所有的坐標(biāo)點都有相對應(yīng)的矩陣格點位置。

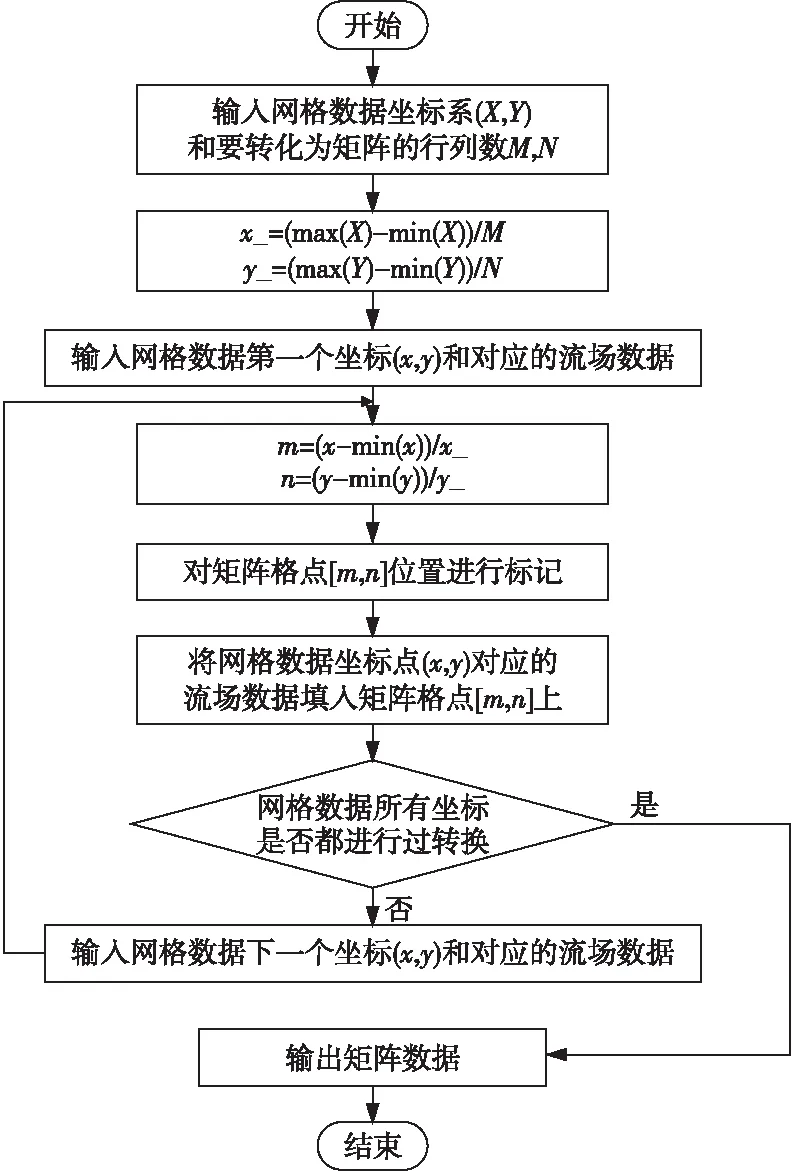
Figure 5 Flow chart of matrixing algorithm 圖5 矩陣化算法流程圖

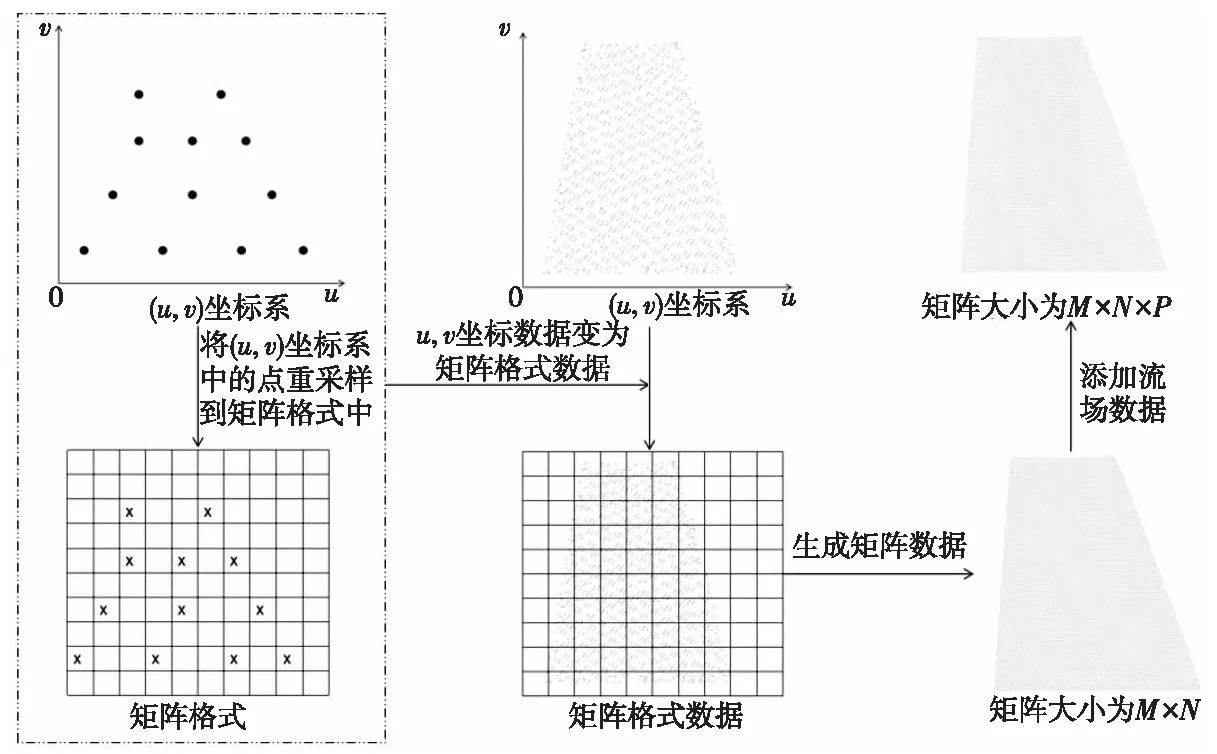
Figure 6 Matrixing of triangular mesh data圖6 三角網(wǎng)格數(shù)據(jù)矩陣化

3.2 矩陣數(shù)據(jù)去稀疏化方法

上文得到的矩陣數(shù)據(jù)可視化后會發(fā)現(xiàn)重采樣后的矩陣數(shù)據(jù)太稀疏，流場數(shù)據(jù)所對應(yīng)的格點分布不密集。為了使重采樣后的矩陣數(shù)據(jù)和原流場數(shù)據(jù)可視化效果相近，需要對矩陣數(shù)據(jù)進行去稀疏化處理。遍歷矩陣的每個格點，使得矩陣每個格點上的元素都為流場數(shù)據(jù)。去稀疏化時需要考慮2種情況，一種是矩陣中存在流場數(shù)據(jù)的格點間隔比較遠，整個矩陣中較稀疏的部分；另一種是矩陣中存在流場數(shù)據(jù)的格點間隔比較近，矩陣中較密集的部分。

圖7為矩陣數(shù)據(jù)去稀疏化示意圖，x為流場數(shù)據(jù)。處理較稀疏區(qū)域：對x1所在的格點進行處理，當(dāng)半徑為R的區(qū)域內(nèi)沒有流場數(shù)據(jù)后將x1填入半徑為r所在的區(qū)域。處理較密集區(qū)域：對沒有流場數(shù)據(jù)的格點進行處理，找到無流場數(shù)據(jù)的格點后，以該格點為圓心，一個格點間距為半徑，按順時針旋轉(zhuǎn)，將碰到的第1個有流場數(shù)據(jù)格點上的數(shù)據(jù)填到圓心處，依次遍歷所有無流場數(shù)據(jù)的格點，最終完成去稀疏化處理。

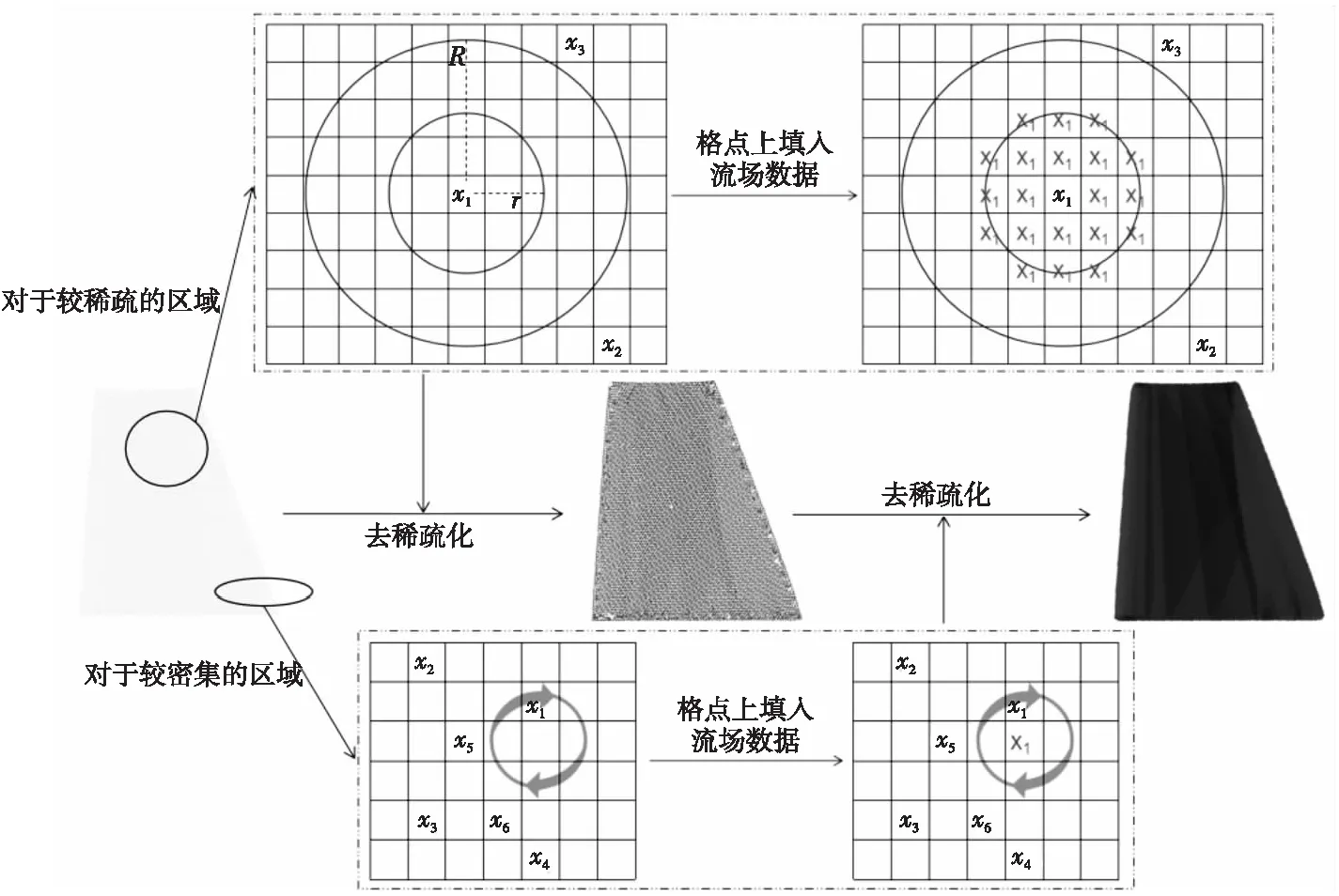
Figure 7 Matrix data de-sparse圖7 矩陣數(shù)據(jù)去稀疏化

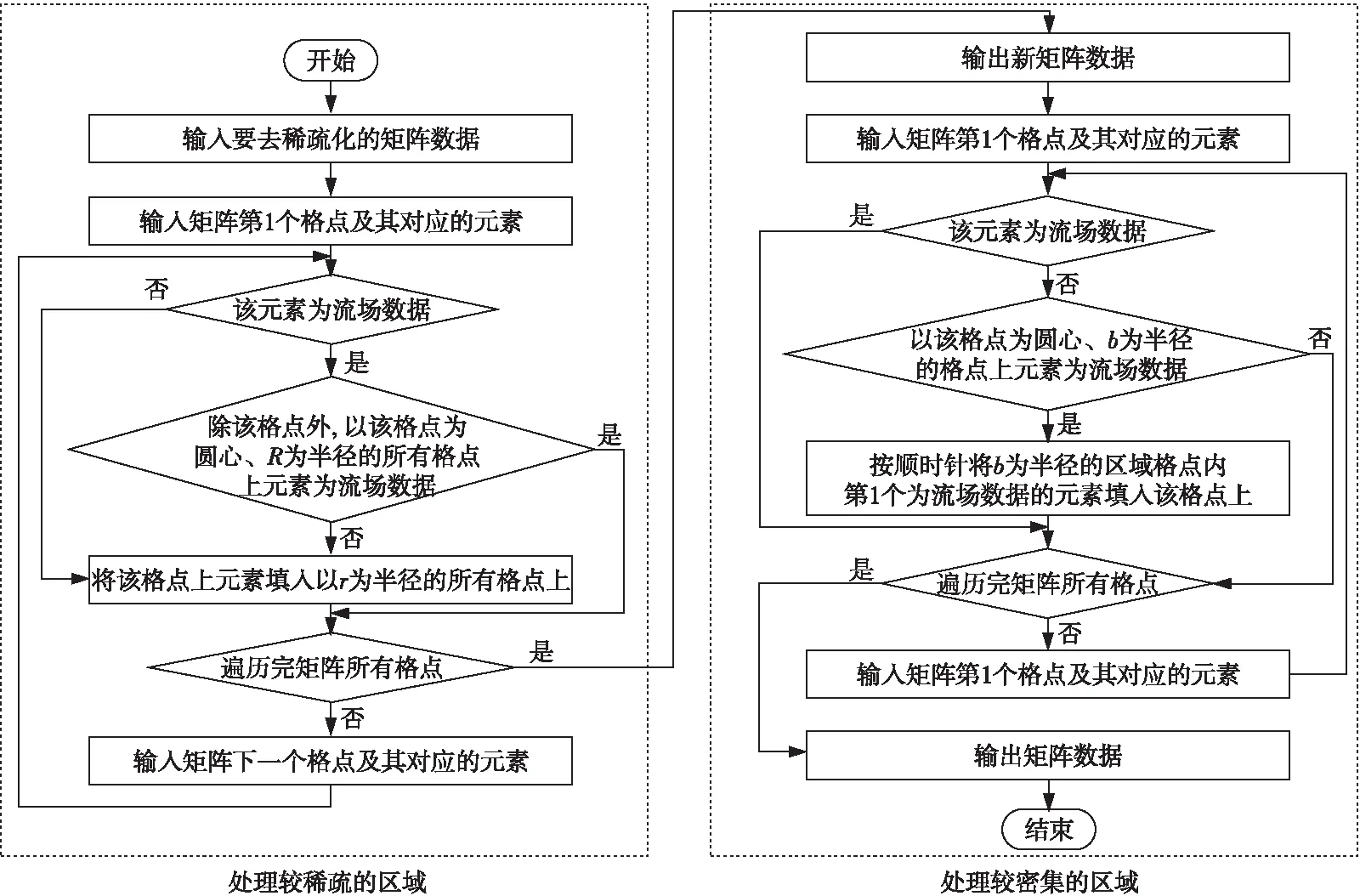
Figure 8 Flow chart of matrix data de-sparse algorithm 圖8 矩陣數(shù)據(jù)去稀疏化算法流程圖

圖8為矩陣數(shù)據(jù)去稀疏化算法流程圖。對于稀疏的部分：遍歷矩陣數(shù)據(jù)中所有元素是流場數(shù)據(jù)的格點，以這些格點為圓心，不同的R(R=2r，r∈N，r<5)值為半徑畫圓(如果r太大，形成的圓區(qū)域過大，區(qū)域格點上肯定存在流場數(shù)據(jù)，所以要將r設(shè)置得小一點)，組成新的格點區(qū)域，如果除圓心處的格點外其他所有格點上的元素都不是流場數(shù)據(jù)，則將半徑為r的圓區(qū)域格點上的所有元素都換成圓心處的格點上的流場數(shù)據(jù)。對于密集的部分：遍歷矩陣數(shù)據(jù)中所有元素不是流場數(shù)據(jù)的格點，以這些格點為圓心，b(b=1，2)為半徑(經(jīng)過第1部分處理后矩陣數(shù)據(jù)中的元素大部分已經(jīng)變?yōu)榱鲌鰯?shù)據(jù)，遍歷完以2為半徑的圓區(qū)域后，所有格點就都可以被流場數(shù)據(jù)賦值)，順時針或逆時針遍歷每個格點，將碰到的第1個為流場數(shù)據(jù)的元素賦值到圓心處的格點上。

4 基于卷積神經(jīng)網(wǎng)絡(luò)的流場分區(qū)模型

4.1 分區(qū)模型結(jié)構(gòu)

在深度神經(jīng)網(wǎng)絡(luò)中，卷積網(wǎng)絡(luò)可以進行特征提取，因此可以利用多層卷積神經(jīng)網(wǎng)絡(luò)來實現(xiàn)特征提取，得到足夠多的特征后再對這些特征進行反卷積，使經(jīng)過卷積層縮小的數(shù)據(jù)還原成原來的大小。通過主干特征提取部分獲得初步的有效特征層；再通過加強特征提取網(wǎng)絡(luò)對得到的初步有效特征層進行上采樣、堆疊和特征融合，獲得最終的特征層；通過卷積最后的特征層進行通道調(diào)整，對數(shù)據(jù)進行智能分區(qū)操作[15]。網(wǎng)絡(luò)模型結(jié)構(gòu)如圖9所示：(1)進行2次3×3的64通道的卷積和1次2×2最大池化；(2)進行2次3×3的128通道卷積和1次2×2最大池化；(3)進行2次3×3的256通道卷積和1次2×2最大池化；(4)進行2次3×3的512通道卷積和1次2×2反卷積；(5)與之前得到的128×128×256矩陣拼接后進行2次3×3的256通道卷積和1次2×2反卷積；(6)與之前得到的256×256×128矩陣拼接后進行2次3×3的128通道卷積和1次2×2反卷積；(7)與之前得到的512×512×64矩陣拼接后進行2次3×3的64通道卷積和1次1×1卷積，以進行通道調(diào)整。

基于卷積神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)的特征是翼型表面物理場的物理信息經(jīng)過降維變化和重采樣后形成的特征圖。通過尋找多物理場中區(qū)域與區(qū)域之間的邊界特征，可以根據(jù)這些重要的物理量進行區(qū)域劃分,使卷積神經(jīng)網(wǎng)絡(luò)更容易對數(shù)據(jù)進行分區(qū)處理。

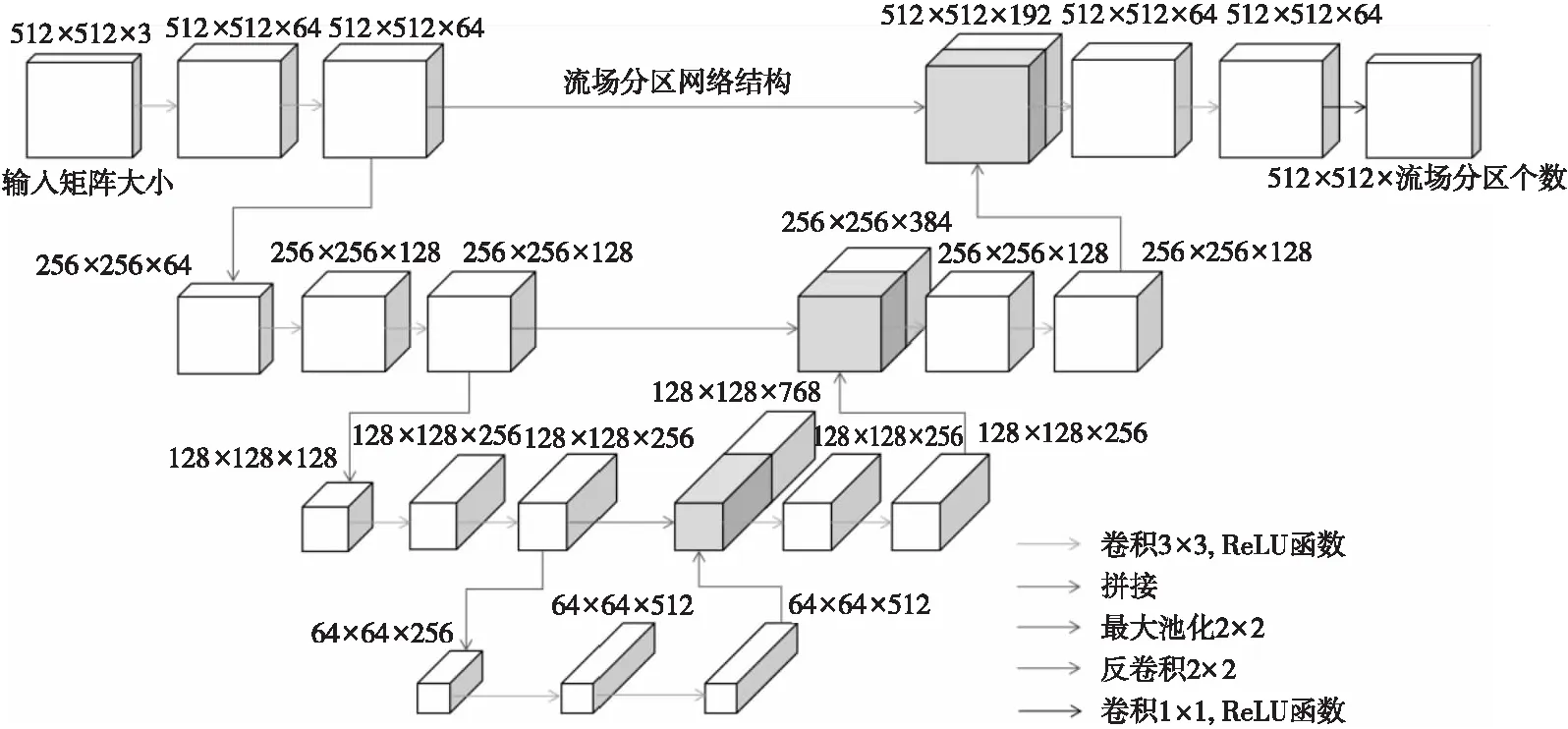
Figure 9 Structure diagram of the proposed model圖9 模型結(jié)構(gòu)圖

本文數(shù)據(jù)集是通過直角網(wǎng)格結(jié)算器的Piflow軟件批量仿真出來的翼型流場數(shù)據(jù)。流場數(shù)據(jù)經(jīng)過降維和矩陣化后得到矩陣數(shù)據(jù)，然后再對矩陣數(shù)據(jù)進行手工標(biāo)記以劃分流場區(qū)域，得到供實驗用的數(shù)據(jù)集。其中數(shù)據(jù)集的90%用于訓(xùn)練，剩余的10%用于測試，最后得到的測試精度為92.62%，測試結(jié)果如表1所示。

Table 1 Test accuracy of the proposed model

4.2 分區(qū)結(jié)果逆映射

流場數(shù)據(jù)經(jīng)過卷積神經(jīng)網(wǎng)絡(luò)進行分區(qū)后得到的分區(qū)結(jié)果是計算結(jié)果的特征分區(qū)，需要將得到的結(jié)果通過逆映射重采樣到三維坐標(biāo)點上，才能使分區(qū)結(jié)果在原機翼翼型上進行可視化展示。

圖10為逆映射算法流程圖。圖11為矩陣數(shù)據(jù)逆映射示意圖。在數(shù)據(jù)矩陣化時對矩陣中元素為流場數(shù)據(jù)的格點進行標(biāo)記；將標(biāo)記后的位置與分區(qū)后的矩陣數(shù)據(jù)進行比較，找到重合的格點位置上對應(yīng)的坐標(biāo)點；再用坐標(biāo)點組成新的三維模型。

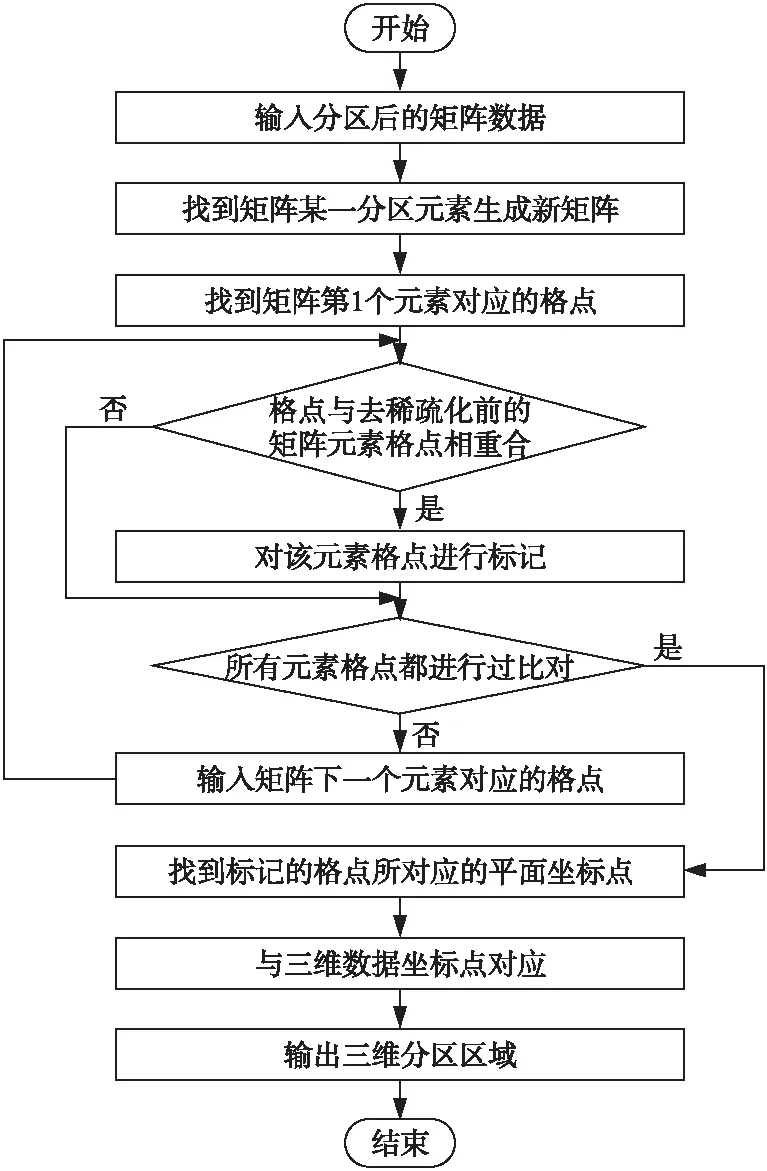
Figure 10 Flow chart of inverse mapping algorithm 圖10 逆映射算法流程圖

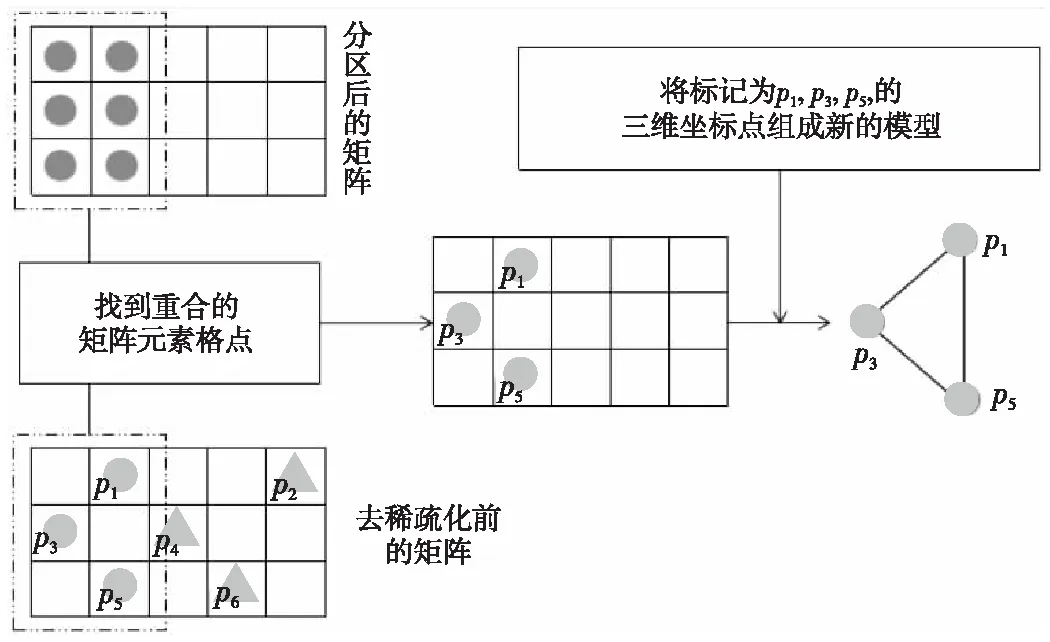
Figure 11 Matrix data inverse mapping圖11 矩陣數(shù)據(jù)逆映射

流場數(shù)據(jù)分區(qū)結(jié)果的可視化效果對比如圖 12所示，圖12a為Piflow生成的流場數(shù)據(jù)，圖12b為手工分區(qū)后的流場數(shù)據(jù)，圖12c為經(jīng)過本文方法智能分區(qū)后的三維分區(qū)區(qū)域與原機翼模型疊加的可視化效果圖。其中，第1個機翼模型有5 309個坐標(biāo)點，手工標(biāo)記的分區(qū)區(qū)域內(nèi)有777個坐標(biāo)點，經(jīng)過實驗后的分區(qū)區(qū)域內(nèi)有693個坐標(biāo)點，正確率為89.2%；第2個機翼模型有7 424個坐標(biāo)點，手工標(biāo)記的分區(qū)區(qū)域內(nèi)有1 208個坐標(biāo)點，經(jīng)過實驗后的分區(qū)區(qū)域內(nèi)有1 064個坐標(biāo)點，正確率為88.1%。

Figure 12 Comparison chart of airfoil partition 圖12 流場分區(qū)對比圖

5 結(jié)束語

本文提出的翼型流場數(shù)據(jù)智能分區(qū)方法，為流場數(shù)據(jù)的后處理和翼型設(shè)計進一步優(yōu)化提供了參考。參數(shù)化批量翼型生成及數(shù)值模擬能夠有效生成翼型訓(xùn)練數(shù)據(jù)集。采用參數(shù)化方法，能夠有效進行流場數(shù)據(jù)降維。通過對流場數(shù)據(jù)進行矩陣化，可以使二維流場數(shù)據(jù)轉(zhuǎn)化為矩陣數(shù)據(jù)，轉(zhuǎn)化后的矩陣數(shù)據(jù)可以作為預(yù)測模型的標(biāo)準(zhǔn)輸入。提出的翼型分區(qū)卷積神經(jīng)網(wǎng)絡(luò)模型能夠有效完成分區(qū)任務(wù)，測試精度達到92%以上。同時,采用數(shù)據(jù)逆映射算法可有效地將矩陣數(shù)據(jù)重采樣到三維表面。

對于流場數(shù)據(jù)的智能分區(qū)而言，本文方法的不足之處在于對處理的流場數(shù)據(jù)的復(fù)雜度有所欠缺。對復(fù)雜的模型而言，參數(shù)化降維比較困難，降維后產(chǎn)生的誤差相對較高。但是，在處理簡單模型時，如機翼等，參數(shù)化降維過程中產(chǎn)生的誤差較小，對分區(qū)的結(jié)果影響不大。針對這些不足，后續(xù)工作將對參數(shù)化方法進行改進。