Lupa q-Bézier曲線的離散卷積生成與求值算法*
耿夢圓,解 濱,韓力文,3,4
(1.河北師范大學數學科學學院,河北 石家莊 050024;2.河北師范大學計算機與網絡空間安全學院,河北 石家莊 050024;3.河北省計算數學與應用重點實驗室,河北 石家莊 050024;4.河北省數學與交叉科學國際聯合研究中心,河北 石家莊 050024)
1 引言
在計算機輔助幾何設計CAGD(Computer Aided Geometric Design)中,Bernstein基函數因其優良性質使得Bézier曲線曲面成為描述自由曲線曲面的重要工具[1-3]。 近年來,q-微積分理論[4]引發眾多研究人員的研究興趣并在超幾何分析、量子力學等領域廣為應用。 其迅猛發展促使基于q-整數的廣義Bernstein算子陸續被提出,其中研究較為廣泛的主要為Lupaq-Bernstein算子和Phillipsq-Bernstein算子。 1987年,Lupa[5]首次提出有理形式的q-模擬Bernstein算子,研究其逼近和保形性質,后被稱之為Lupaq-Bernstein算子。 Ostrovska[6]和Wang等[7]探究了算子的一致收斂性及收斂速度等問題。 1996年Phillips[8]引入基于q-整數的多項式形式的q-Bernstein算子,可由q-差分簡單表示,為便于區分,本文稱之為Phillipsq-Bernstein算子。 隨后Oru?等[9]構造出Phillipsq-Bézier曲線,引起研究人員的關注與研究。 在此帶動與影響下,帶有形狀參數的廣義Bézier曲線曲面在曲線曲面造型上發揮了重要作用。
2014年,Han等[10]依據Lupaq-Bernstein算子構造出基于q-整數的Lupaq-Bézier曲線曲面,得到了曲線的幾何不變性、升階等性質及de Casteljau算法等。 相比于Phillipsq-Bézier曲線,Lupaq-Bézier曲線的函數類型、形狀參數q的取值范圍及端點相切的性質均不同:(1) Phillipsq-Bézier曲線為多項式形式且參數q∈(0,1],而Lupaq-Bézier曲線為有理函數形式且q∈(0,+∞),取值范圍更廣;(2) Phillipsq-Bézier曲線僅與首控制邊相切,而Lupaq-Bézier曲線與首末控制邊均相切。
2 預備知識
2.1 Lupa q-Bézier曲線的相關定義
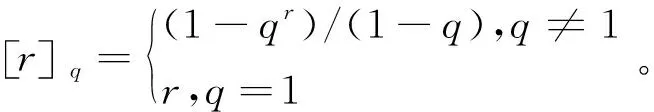
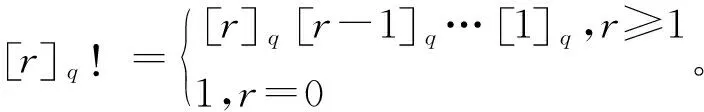
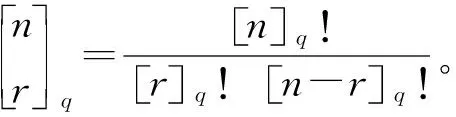
特別地,q-二項式系數滿足Pscal-type關系式,如式(1)和式(2)所示:
(1)
(2)
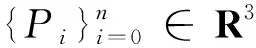
(3)
為n次Lupaq-Bézier曲線,其中:
(4)
為n次Lupaq-Bernstein基函數。 當q=1時,Lupaq-Bézier曲線退化為經典Bézier曲線。
2.2 離散卷積的相關定義
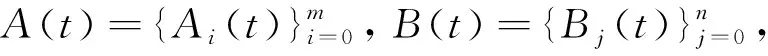
(5)
離散卷積滿足交換律及結合律,如式(6)和式(7)所示:
A(t)?B(t)=B(t)?A(t)
(6)
A(t)?(B(t)?C(t))=(A(t)?B(t))?C(t)
(7)
定義6[20]離散卷積的微分法則,如式(8)所示:
(A(t)?B(t))′=
A′(t)?B(t)+A(t)?B′(t)
(8)
3 離散卷積生成Lupa q-Bézier曲線
3.1 Lupa q-Bernstein基函數的離散卷積形式
根據q-二項式系數滿足的Pascal-type關系式(1),給出Lupaq-Bernstein基函數的遞推關系。
引理1[10]n次Lupaq-Bernstein基函數是2個n-1次Lupaq-Bernstein基函數的仿射組合,如式(9)所示:
(9)
利用此遞推關系式,從零次基函數開始,依次向高一次的基函數遞推,得到Lupaq-Bernstein基函數的向下遞推三角形,如圖1所示。 從上至下第i層的中間節點恰好是第i次的Lupaq- Bernstein基函數。

Figure 1 Downward recurrence of Lupa q-Bernstein basis functions圖1 Lupa q-Bernstein基函數的向下遞推
n次Lupaq-Bernstein基函數出現在第n層向下遞推三角形的底部。 同時,基函數是由頂端到底部第i個位置的所有路徑乘積之和,例如,對于4次Lupaq-Bernstein基函數式(10)成立:
(10)
結合定義5,此過程等同于函數序列離散卷積的計算過程,由此構造出Lupaq-Bernstein基函數的離散卷積形式。
定理1設函數序列如式(11)所示:
k=1,2,…n
(11)
則Ak(t;q)可離散卷積生成n次Lupaq- Bernstein基函數序列,如式(12)所示:
A1(t;q)?…?Ak(t;q)?…?An(t;q)
(12)

注1當q=1時,式(12)退化為經典Bernstein基函數的離散卷積形式[20]。
注2文獻[15]主要圍繞Lupaq-Bernstein基函數的離散概率模型給出離散卷積形式。本文則是從基函數的向下遞推結合路徑角度得到該形式,同時在下文中將進一步發揮離散卷積表示與向下遞推三角形的作用,探究Lupaq-Bézier曲線的特點與優良性質。
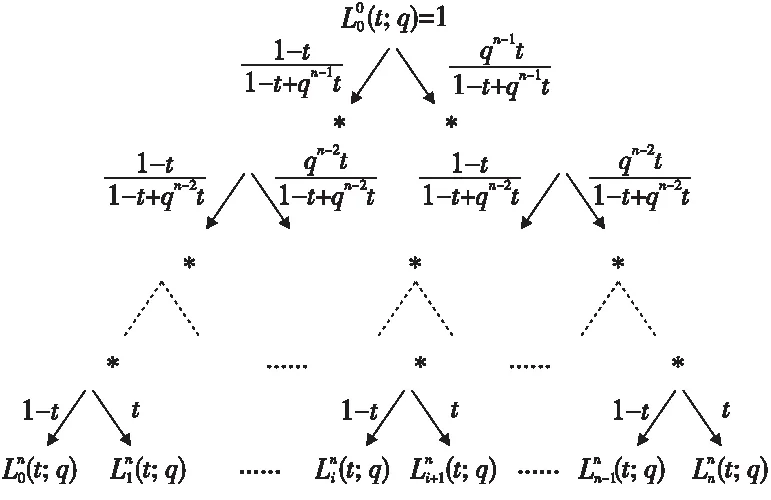
Figure 2 Basis functions constructed by convolutionof function sequences in reverse order圖2 函數序列逆序卷積構造的基函數
3.2 Lupa q-Bézier曲線的de Casteljau算法
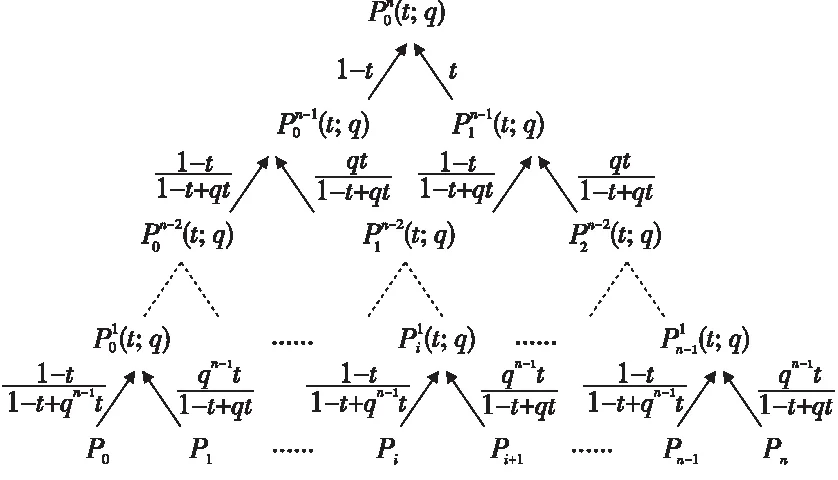
Figure 3 A de Casteljau algorithm for Lupa q-Bézier curve圖3 Lupa q-Bézier曲線的一種de Casteljau算法
定理2對于任一條n次Lupaq-Bézier曲線,基于離散卷積可生成n!種de Casteljau算法。
(13)
如圖4所示,當以圖2定義的離散卷積順序構造時,de Casteljau算法具有顯式矩陣表示[12],記為de Casteljau算法2,如式(14)所示:
(14)
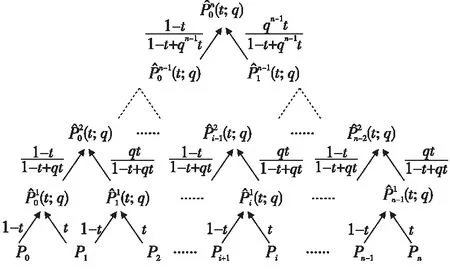
Figure 4 de Casteljau algorithm with explicit matrix representation圖4 具有顯式矩陣表示的de Casteljau算法
注3定理2所提出的n!種de Casteljau算法在計算Lupaq-Bézier曲線上任意點的效率上是一致的,針對不同的使用需求可選擇不同的算法。
例1對于一條形狀參數q=4的3次Lupaq-Bézier曲線,可生成3!種de Casteljau算法,如圖5所示,‘o’點為不同算法求得的曲線上的同一點。
與經典Bézier曲線de Casteljau算法求得切點[21]不同,Lupaq-Bézier曲線de Casteljau算法倒數第2層2節點構成的直線段與曲線相交于2個點,本文將這2個交點統稱為割點。 如圖5所示,不同的de Casteljau算法得到的割點不同,有時為左割點,有時為右割點。 第5節將給出2種de Casteljau算法,分別求得左/右割點的判定條件。
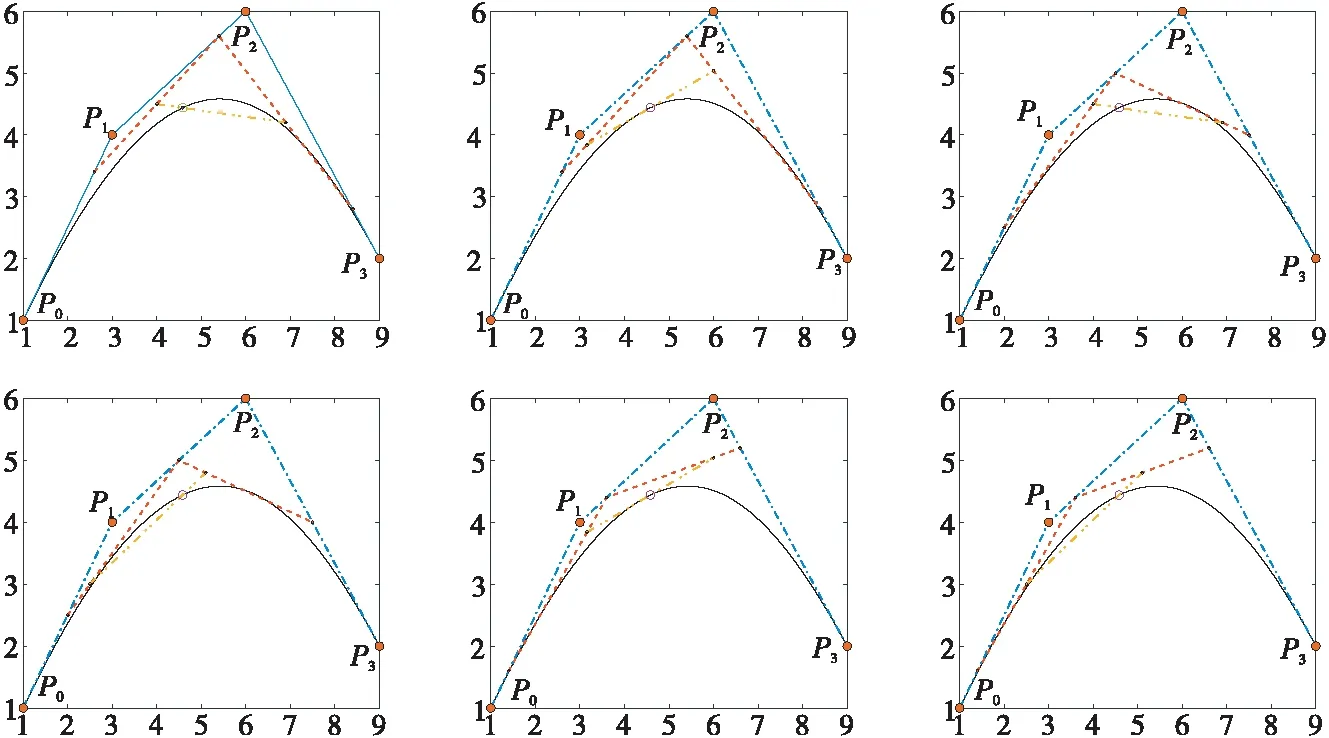
Figure 5 3! de Casteljau algorithms for cubic Lupa q-Bézier curve圖5 3次Lupa q-Bézier曲線的3!種de Casteljau算法
4 速端曲線
定理3設n次Lupaq-Bézier曲線的一階速端曲線表達式如式(15)所示:
(15)
Aj-1(t;q)?Bj(t;q)?Aj+1(t;q)?…?An(t;q)
(16)
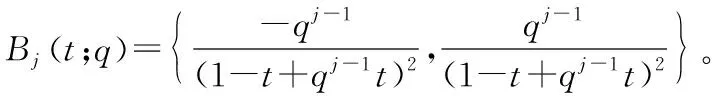
(17)
(18)
當q=1時,該速端曲線是以原曲線控制頂點的向前差分ΔP0和ΔP1為首末控制頂點的一次Bézier曲線;當q∈(0,1)∪(1,+∞)時,二次Lupaq-Bézier曲線的速端曲線是以P′(0;q),P′(1;q)為首末端點的直線段。
除此之外,通過定理3進一步整理可得到首末2個n次Lupasq-Bernstein基函數的導函數的顯式表達式。
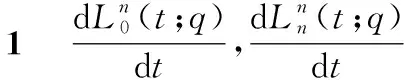
(19)
(20)
根據離散卷積的微分法則可在基函數一階導序列式(16)的基礎上繼續微分,得到基函數的高階導數,進而計算Lupaq-Bézier曲線的高階導矢。
定理4Lupaq-Bernstein基函數的二階導函數序列的離散卷積結構如式(21)所示:
(21)
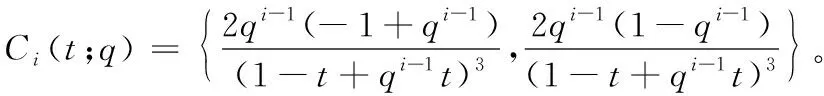
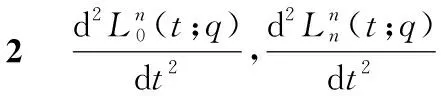
(22)
(23)
5 de Casteljau算法左/右割點分類
圖3與圖4為曲線具有的2種de Casteljau算法。 圖6a和圖6b分別展示了不同形狀參數q下的二次Lupaq-Bézier曲線,其中q=1所表示的曲線為經典Bézier曲線。 由圖6可知,Lupaq-Bézier曲線始終位于控制多邊形與經典Bézier曲線之間,并且通過選取不同的形狀參數q值,可以任意調整曲線形狀,增加曲線造型的靈活性[10]。
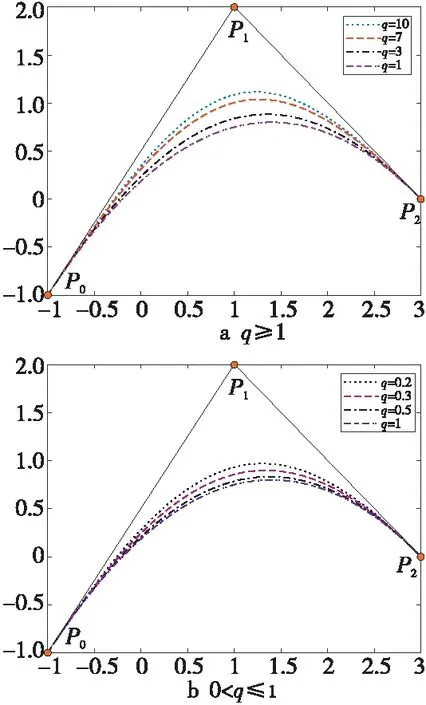
Figure 6 Quadratic Lupa q-Bézier curves with different shape parameters圖6 不同形狀參數的二次Lupa q-Bézier曲線
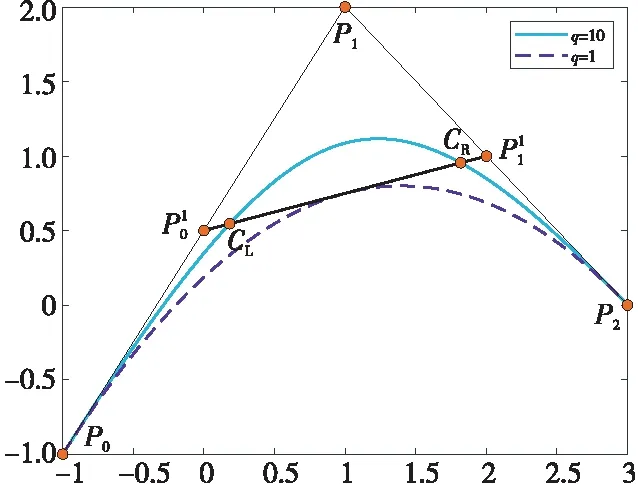
Figure 7 Comparison of de Casteljau algorithmsbetween Lupa q-Bézier curve and classical Bézier curve圖7 Lupa q-Bézier曲線與經典Bézier曲線de Casteljau算法對比
下面分別給出de Casteljau算法1和算法2得到左割點或右割點時的充分必要條件。
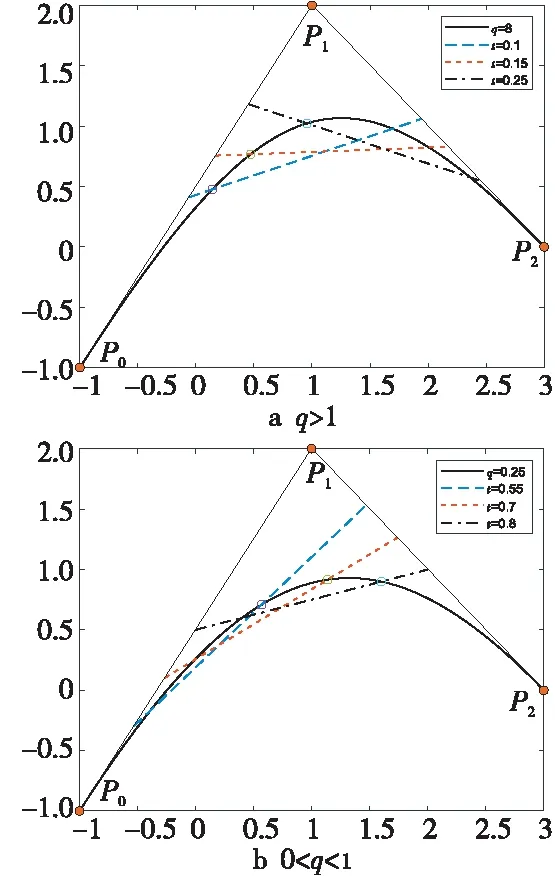
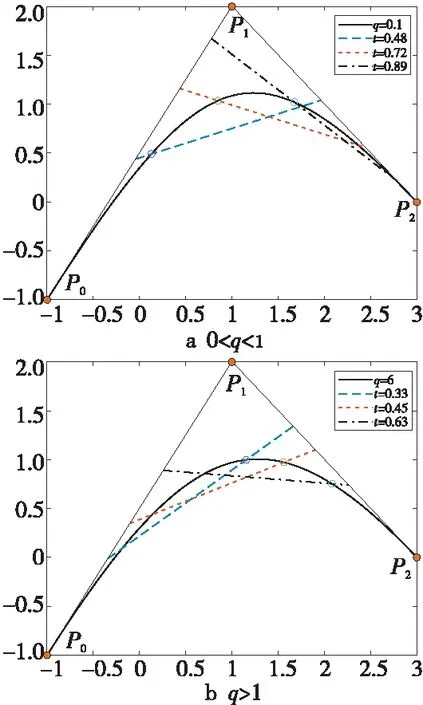
定理5任意給定參數t∈(0,1),de Casteljau算法1求得左割點當且僅當形狀參數q>1;求得右割點當且僅當0 證明對比Lupaq-Bézier曲線de Casteljau算法1與經典Bézier曲線de Casteljau算法,為便于區分,記二次經典Bézier曲線de Casteljau算法節點為和 (24) (25) 定理6任意給定參數t∈(0,1),de Casteljau算法2求得左割點當且僅當形狀參數0 (26) (27) 注4Lupaq-Bézier曲線具有端點插值性,即當參數t=0時,de Casteljau算法1或算法2求得參數對應曲線上一點為P0;t=1時,算法1或算法2求得曲線上一點為P2。 圖8a和圖8b展示了de Casteljau算法1分別在q>1時取不同參數t得到的左割點和0 Figure 8 Left/right cut points gotten by de Casteljau algorithm 1 圖8 de Casteljau算法1得到的左/右割點 Figure 9 Left/right cut points gotten by de Casteljau algorithm 2 圖9 de Casteljau算法2得到的左/右割點 上述定理5和定理6分別給出了de Casteljau算法1和算法2得到左割點或右割點時形狀參數 的取值范圍。 算法3雙割點算法 輸入:控制頂點P0,P1,P2,參數t,q。 輸出:左/右割點CL,CR。 步驟3計算另一割點 步驟4根據形狀參數的取值范圍判斷,倘若q≥1,則CL=C1,CR=C2;若0 定理7給定二次Lupaq-Bézier曲線P(t;q),其中q∈(0,+∞),t∈(0,1),應用雙割點算法3時,節點與左/右割點CL,CR構成的交比固定。 證明當q>1時,利用雙割點算法3中的步驟2與步驟3得到2個割點且CL=C1,CR=C2,則式(28)和式(29)滿足: (28) 0 (29) 證畢。 本文通過引入向下遞推三角形和離散卷積函數序列,提出n次Lupaq-Bernstein基函數的離散卷積結構,并將向下遞推三角形反轉箭頭方向自下而上卷積生成Lupaq-Bézier曲線。 借助離散卷積的交換性,進而得到n!種新的de Casteljau算法。 文中列舉出了其中的2種算法及其優勢,對于其他算法的特征有待進一步探究。 根據對2種de Casteljau算法及其形狀參數q的討論,二次Lupaq-Bézier曲線可選擇性得到左/右割點。 另外給出同時計算2個割點的算法,并證明雙割點算法具有交比不變性。 本文僅得到2個n次基函數導數的顯式表達式。 對于其他基函數導數的具體形式還有待探究。 對于3次或更高次Lupaq-Bézier曲線的割點討論及其應用需要進一步研究。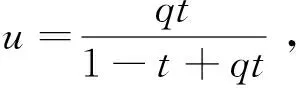

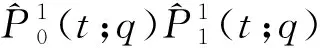
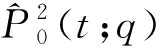
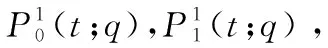
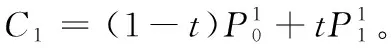
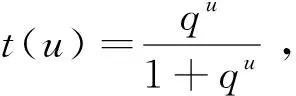
6 結束語

