動力電池低荷電狀態風險預測

任 超

（長安大學 汽車學院，陜西 西安 710064）

隨著我國大力推廣新能源汽車，以及出臺補貼、牌照豁免和購買稅等優惠政策，我國新能源汽車數量迅速增長。到2019年6月為止，我國新能源汽車數量已達到344萬輛。純電動汽車約281萬輛，占新能源汽車的81.74%。它們是新能源汽車的主要組成部分，也是本文的研究對象。但是，由于制造商在銷售電動汽車時宣傳的標準行駛里程與實際巡航范圍相去甚遠，以及汽車報警信息的不完善，導致了車主的在行駛過程中，會長時間以一個低電量行駛。電動汽車長時間低電量行駛會降低電池的壽命，加快電池的損壞。這樣對動力電池是一個很大的損害，會間接造成對環境的污染。為了解決上述問題，基于國家新能源汽車大數據聯盟提供的真實行車數據，本文采用基于數據的方法建立時變模型、行駛距離、電池電壓、電池電流來從多個角度反映動力電池當前剩余電量荷電狀態（State Of Charge, SOC）的工作狀況。通過比對分析，電動汽車上應用最多的是磷酸鐵鋰電池，因此，本文選擇磷酸鐵鋰電池為研究對象。

目前，動力電池SOC的估計方法可分為安培小時法、開路電壓法、內阻法、線性模型法、卡爾曼濾波法，以及使用神經網絡支持向量機智能算法估計動力電池的SOC[1]。李靖建立了二階戴維南等效電路模型，通過實驗數據復現出了電池的開路電壓-電池的荷電狀態（Open Circuit Voltage-State Of Charge, OCV-SOC）關系，結合其他估計算法，對單體磷酸鐵鋰電池的SOC進行了估計[2]。

上述文獻主要基于在諸如實驗或仿真工具的理想條件下獲得的單電池的充電和放電數據來估計SOC。對車輛動力蓄電池SOC的實際運行結果估計提供的指導很少。

一些學者研究新歐洲駕駛循環周期（New European Driving Cycle, NEDC）固定模擬條件下單體電池的SOC估計，獲得的估計精度是較好的，但這忽視了實際駕駛條件的復雜性和可變性，很難將研究結果應用于實踐[3]。

此外，上述研究均基于單動力電池的SOC估計，對于單體電池的SOC估計在應用于整個電池組的SOC估算時無效[4]。

本文從動力電池系統整體和實際應用的角度出發，脫離理想的實驗環境，根據新能源汽車國家大數據聯盟采集的實車運行數據，采用大數據的分析方法。這種方法優點在于，只關注動力電池組系統的整體行為，使用主成分分析法（Principal Component Analysis, PCA），分析出來表征低SOC的特征參數。使用邏輯回歸算法，總結出來動力電池低SOC時各個特征參數的規律，并用總結出來的規律對實車進行預測。使用該方法，無需對單電池的復雜非線性特性、電池組的物理結構和電化學知識等進行考慮，該算法適合于實際運行的整個電池組，充分考慮了汽車真實的行駛時各環境因素的影響。

1 算法理論依據

1.1 主成分分析

新能源汽車大數據聯盟所提供的數據特征值較多，達到34個，每個特征都用來分析不現實，也會加大工作量，所以要進行數據的降維處理，篩選出相關性不高的幾個特征參數進行分析。因此，選用PCA進行數據的降維處理。

PCA即主成分分析方法，是一種使用最廣泛的數據降維算法。主成分分析的基本思想是在盡可能表示原特征的條件下，將原始特征經過一定的算法變化映射到低緯度空間。PCA源于通信理論的K-L變換。其問題可以描述為對于d維空間中的n個樣本，考慮如何能在低維空間中更好地表示它們。

任何形式的變化在數學上都可以抽象成一個映射，或者函數。構建一個函數f(Xm×n)使得這個函數可以將矩陣Xm×n降維，矩陣Xm×n中有m個樣本，每個樣本有n個特征值。所以，所謂的降維，其實是減少n的數量。假設降維后的結構Zm×k，其中k＜n。那么PCA的數學表達可以表示為

為了找到上面說的f(x)，需要做一些工作，在線性空間中，矩陣可以表示為一種映射，所以上面的問題可以轉化為尋找這樣一個矩陣W，該矩陣可以實現上面的映射目的：

假設要把矩陣的維數降為1，也就是最后每個樣本只有一個屬性，即k=1。目標是使降維后的數據在那個坐標軸中的分布盡可能分散，數據分布的離散程度我們用方差來衡量。現在的目標：

最大化新坐標軸上的方差，就是讓數據更加分散：

將問題轉換為

最終目標轉化為

通過求解Lagrange函數，得到結果為Cov(x)ω-αω=0。

令Cov(x)ω=S，Sω-αω=0正好是特征值的定義，也就是α是矩陣S的特征值，ω是矩陣S的特征向量。但是特征值很多，ω到底是哪一個特征值。

同樣道理，如果是需要將數據映射為2維數據，還是求解上述的最大化方差。

原始數據包含34個特征參數，降維后的特征參數只有12個，如表1所示，極大地提高了分析的速度。

表1 降維后的特征參數

1.2 皮爾遜相關系數

皮爾遜相關也稱為積差相關（或積矩相關）是英國統計學家皮爾遜于20世紀提出的一種計算直線相關的方法。

如果兩組數據X:{X1,X2,…,Xn}和Y{Y1,Y2,…,Yn}是總體數據（例如普查結果）那么最后均值為

協方差：

皮爾遜相關系數：

σx是X的標準差，σY是Y的標準差。觀察皮爾遜相關系數的公式：我們發現皮爾遜相關系數可以看成消除了兩個變量量綱影響，即將X和Y標準化后的協方差。因此，兩個變量相關的程度可以使用皮爾遜相關系數來衡量。

皮爾遜相關系數在為-1到1之間波動。系數值1表示變量間呈現正相關；系數值為-1表示變量間呈現負相關。系數值為0意味著兩個變量之間沒有關系。

皮爾遜相關系數的使用條件是變量之間服從正態分布。因為所采集的數據量極大，所以可近似地認為變量之間的分布服從正態分布，可以使用皮爾遜相關系數進行分析。

如下所示為相關系數分析結果：系數值為0意味著兩個變量之間沒有關系。

0.8～1.0，極強相關；0.4～0.6，強相關；

0.2～0.4，弱相關；0.0～0.2，極弱相關。

1.3 邏輯回歸算法

邏輯回歸算法使用對數概率比線函數進行擬合變量間的關系[5]。如下所示：

激活函數：sigmoid函數，表達式為

回歸的結果輸入到sigmoid函數中，最終的輸出結果為[0,1]區間的一個概率值，默認0.5為閾值。

1.4 算法的步驟

步驟1：將收集到的原始數據進行清洗后，用PCA隨數據的特征進行降維，以減少特征參數的個數；

步驟2；對降維后的數據再次進行皮爾遜相關系數的分析，分析出低SOC值時的影響因素，進一步達到降維的目的；

步驟3：按照8:2比例隨機分開初步篩選后的數據，其中一部分作為訓練集，另一部分則為測試集；

步驟4：利用邏輯回歸算法，建立可以識別動力電池低SOC的模型。

2 算例及分析

為了驗證和檢驗算法的可行性和區分效果，文中提取了低SOC報警車輛的信息，并進行了相應的特征提取。然后隨機抽取數據進行實驗。

單獨使用邏輯回歸算法對選取的數據進行求解，對報警的信息進行分類。

2.1 皮爾遜相關系數分析

通過SOC的信息已與各個特征參數之間的相關系數比較分析，選擇最高電壓，最低電壓與電池溫度作為描述電池低SOC值的特征參數。

2.2 參數分析

對報警車輛的最大電壓值做散點記錄，從這半年左右的數據記錄中發現，電池電壓最大值普遍集中在3.475 V量離群點分析在3.500 V之上。電壓最小值及其于3.45 V離散點分布在眾數之下。同樣的，我們描述了電池最大溫度與最小溫度的數據分布，電池溫度最大值分布比較零散，在一小段時間內變化平穩，七月后，電池溫度最大值呈現線性上升趨勢，而在進入秋季，九月左右出現非線性波動下降情況。

2.3 算法求解

首先需要數據歸一化，將特征參量轉換為無量綱的數據，然后數據按照8:2的比例分組。訓練組用于算法參數的訓練，數據量有5 074行；測試組用于算法的檢驗，數據量有1 269行。模型在訓練過程的損失曲線如圖2所示，可以發現，隨著訓練時間的延長，訓練過程中的損失逐漸下降。

圖2 Loss曲線

邏輯回歸輸入：

式中，x1，x2，x3分別表示最大電壓值、最大溫度值、最小電壓值，將5 076組訓練組數據輸入模型中，得到模型的權重和偏置：

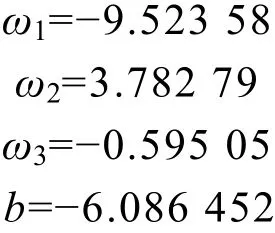
得到輸入函數：

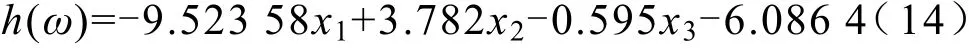
將得到的輸入函數h(ω)代入到sigmoid函數g(ω)中。

若g(ω)＞0.5，輸出1，表示報警；

若g(ω)＜0.5，輸出0，不報警。

用訓練好的模型應用在測試集上，在1 269組測試集中，有兩組預測結果出錯。

精確率和召回率是兩個評估模型好壞的重要標準。

精確率（precision）：預測正確的個數占總的正類預測個數的比例。

召回率（recall）：真實為正例的樣本中預測結果為正例的比例。

該模型的精確率和召回率分別達到了99%和99.8%高的水平，表示該模型可以應用到實際中。

3 結束語

本文基于國家新能源汽車大數據平臺的大量數據，基于邏輯回歸算法，對實際復雜多變工況下動力電池的運行過程進行低SOC值下的特征參數統計，并建立了模型。該模型可以用來預測汽車在真實行駛工況下是否出現低SOC的情況，并進行報警。防止汽車在行駛過程中處在一個低SOC狀態行駛，對電池造成潛在的傷害。

雖然本文模型的估計結果良好，但仍存在一些局限性和需要改進的地方。對于數據質量好壞的確定沒有理想的參考標準。連接到大數據聯盟的汽車數量已達百萬級別。汽車本身的行駛使得車內硬件質量下降將導致收集數據的誤差是不可避免的事，這也是與實驗室條件的差異。盡管本文進行了數據清理工作，但是原始數據的質量是模型結果準確性的根本保證。未來，作者希望通過單車行駛試驗，收集高質量數據將誤差控制在較小的范圍內，從而克服這一問題。