基于機器視覺的直齒輪齒距偏差檢測＊

逯海濱 張 丹 李長安 隋文濤 竇亞萍 張宇凡

（①山東理工大學機械工程學院，山東 淄博 255049；②山東理工大學電氣與電子工程學院，山東 淄博 255049）

齒輪是現代工業生產中最常見的零部件[1]，作為現代工業系統的核心零部件，其結構設計水平和加工精度是決定機械產品性能的決定性因素之一。由于齒輪的幾何結構復雜，測量參數繁多，測量結果的準確性直接關系到齒輪的制造精度和各種性能，因此，快速、準確地測量和分析齒輪的參數和精度具有重要意義。

齒距偏差是評定齒輪精度的幾何元素之一，對其進行齒距偏差檢測至關重要。為了避免人為因素對測量結果造成影響，實現齒輪在線測量，提高齒輪齒距偏差測量的準確率，研究人員引入了機器視覺使用非接觸測量來代替傳統的接觸測量[2-4]，并取得了一定的進展。文獻[5]設計了一種基于機器視覺的齒輪測量系統；但是該系統在面對鏡頭畸變時無法進行校正，測量精度低。文獻[6]搭建的基于機器視覺的齒輪參數測量系統，可以實現各項參數的測量，測量精度可達0.1 mm。文獻[7]使用最小二乘法擬合得到了齒頂圓、齒根圓的半徑；但該方法會受到輪廓曲線提取效果的影響，造成較大誤差。

針對齒距偏差檢測中存在的問題，本文以標準直齒輪為對象，研究了基于機器視覺的齒距偏差研究方法。并引入改進的Zernike亞像素邊緣檢測算法[8-10]，測量得到了齒輪的參數，對進一步提高齒距偏差測量準確性及可靠性具有重要的現實意義。

1 測量系統構成及測量流程

1.1 測量系統構成

本文齒輪齒距偏差測量裝置[11]如圖1所示，主要由CCD工業相機、鏡頭、環形光源、工作臺和計算機等組成。工業相機通過螺栓固定在支架上，其高度通過轉動手輪來調節。測量過程中，將待測齒輪放至工作臺上，調節相機高度及光源亮度使得拍攝的圖像最為清晰，并將采集到的圖像傳輸到計算機上，基于計算機，對采集到的齒輪圖像進行處理并測量出齒輪參數。

圖1 機器視覺裝置構成圖

1.2 測量流程

根據齒距偏差測量原理制定測量流程，測量流程圖如圖2所示。

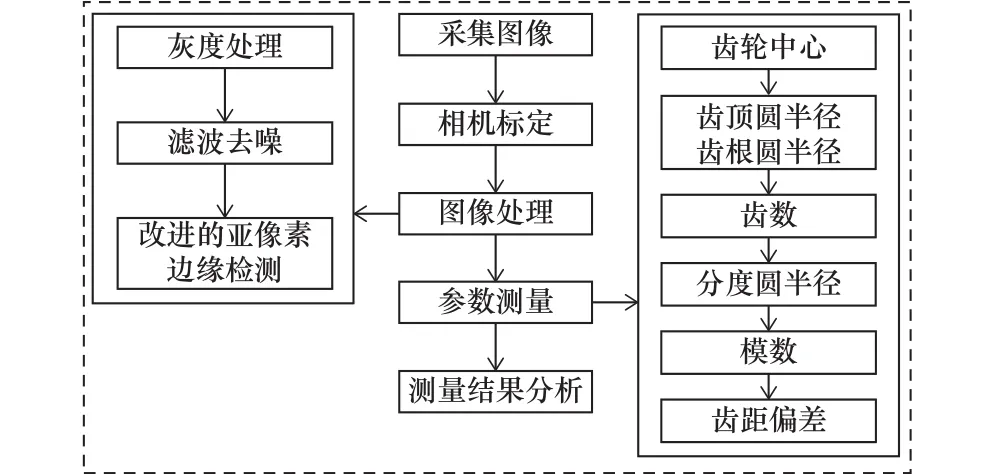
圖2 測量流程圖

2 相機標定與圖像預處理

2.1 畸變校正

為了提升對圖像的測量精度，減少鏡頭畸變的影響，需要對圖像進行畸變矯正[12]。本文采用基于張正友法的相機標定[13]，畸變校正流程如圖3所示。

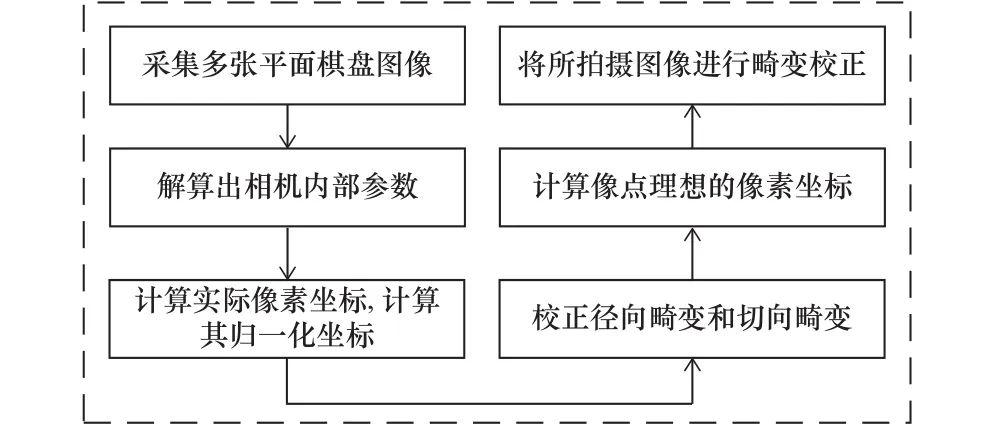
圖3 畸變校正流程

在校正過程中，矯正畸變通過泰勒展開式取前3項。徑向畸變校正中，畸變通過泰勒級數展開式校正為

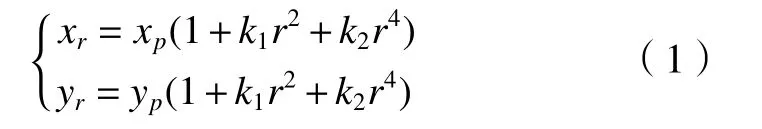
在切向畸變校正中，畸變通過泰勒級數展開式校正為

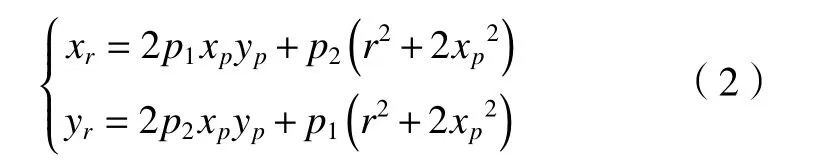
式中：k1、k2為徑向畸變系數；p1、p2為切向畸變系數；(xr,yr)、(xp,yp）為歸一化處理的無畸變像點和實際像點坐標；r為無畸變像點坐標與光學中心的距離。

2.2 像素當量標定

測量齒輪齒距偏差的過程中，需要實現像素坐標尺寸到實際尺寸的轉換。

使用Harris角點檢測算法[14]對校正后的棋盤格進行角點檢測，將提取出的角點作為像素當量標定的特征點。通過計算任意兩個相鄰的同行角點間的物理尺寸和像素數量，得到棋盤格上此行的像素當量，計算多個同行角點的像素當量并取平均值。所得結果即為系統像素當量，測得本系統像素當量：K=0.018 mm/pixel，計算如式（3）所示。

式中：K為系統像素當量；Ki為同行相鄰角點的像素當量；S為相鄰角點物理尺寸設計值；Pi為相鄰角點像素數量。

2.3 圖像預處理算法

本文采用工業相機在背景光源照射下采集，待測圖像如圖4a所示，在獲取待測圖像后，對圖像進行預處理算法，提升待測圖像的質量。為提升圖像處理速度，對圖像進行灰度化處理。

圖4 圖像預處理結果

為避免噪聲干擾對圖像質量的影響，改善圖像清晰度。本文選擇中值濾波對圖像進行濾波去噪處理，圖像預處理后的灰度圖如圖4b所示。

3 改進的Zernike矩亞像素邊緣檢測算法

3.1 Zernike矩邊緣檢測算法原理

對于離散函數f(x,y)，其n階m次Zernike矩可以定義為

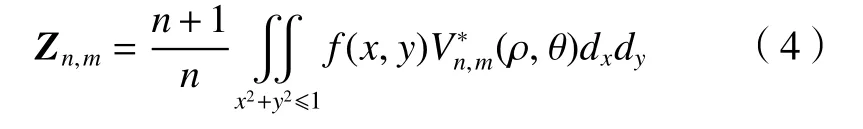
式中：V* n,m(ρ,θ)為核心公式的共軛；ρ為圓點到點（x，y）的距離；θ為矢量ρ與x方向的夾角。

如圖5a所示為Zernike矩理想邊緣模型，圖5b為圖像繞坐標軸旋轉θ角后的邊緣階躍模型，目標區域用陰影區域表示，h表示圖像背景區域的灰度值，k是邊緣階躍高度，l是邊緣線到原點的垂線長度，θ為邊緣線到原點的垂線與x軸的夾角。

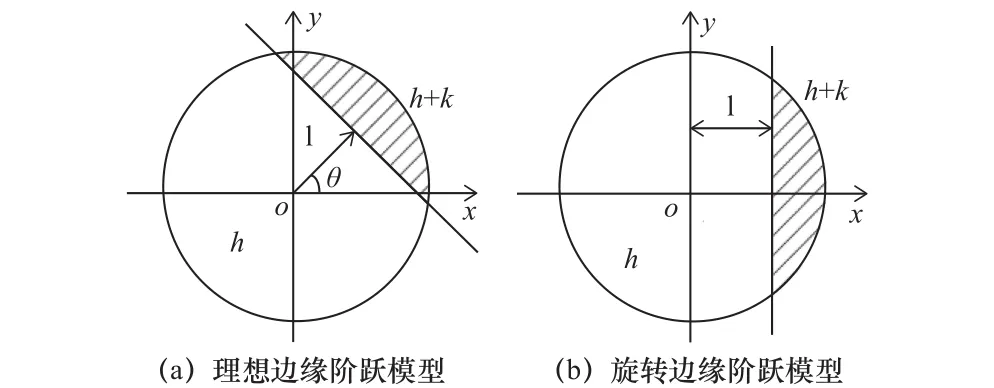
圖5 Zernike矩理想邊緣模型

設邊緣階躍模型繞坐標軸旋轉θ角，根據Zernike矩旋轉不變性可得

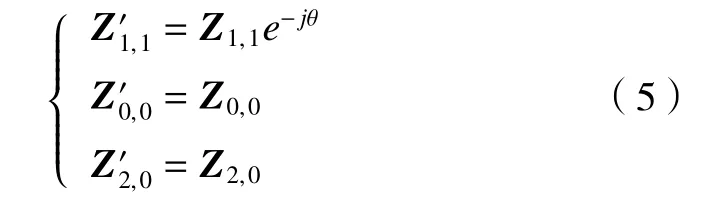
由式（5）中可知旋轉后的圖像關于x軸對稱，并且只有相角發生了變化。將旋轉后的理想邊緣階躍模型積分可得

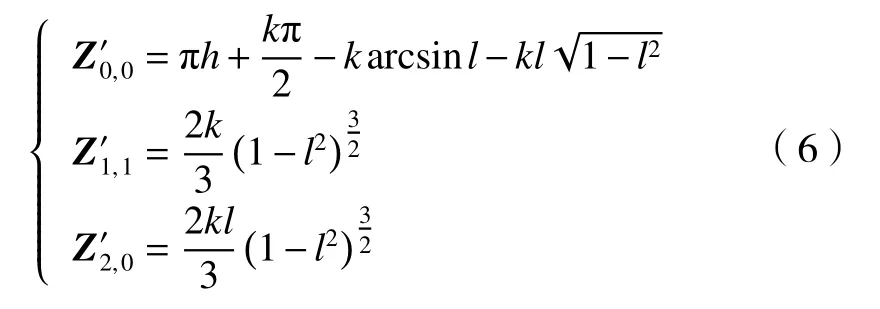
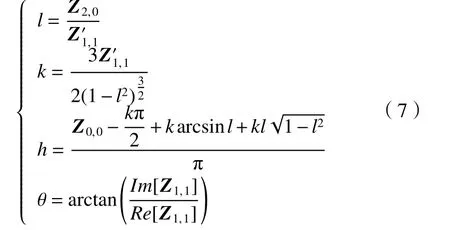
基于Zernike矩的模板效應，需要對亞像素坐標進行修正，利用式（7）對各項參數進行運算，求得修正后的亞像素邊緣坐標為

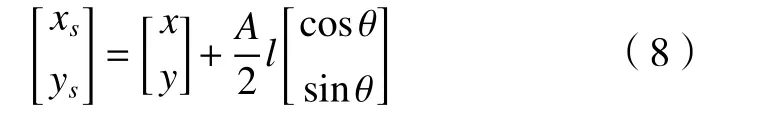
式中：A為模板階數，本文采用7×7模板階數。（xs,ys）為修正后圖像的亞像素邊緣坐標。

3.2 基于運算時間的改進

傳統的Zernike亞像素邊緣檢測算法需要遍歷計算所有像素點的多個正交復數矩，計算效率低且計算時間長。為了減少運算時間，提高亞像素邊緣檢測的效率，本文引入Canny邊緣檢測算法，通過Canny算子對預處理過的圖像進行檢測來實現粗定位，從而將 Canny邊緣檢測與Zernike 矩亞像素邊緣檢測相結合。收集并保存所有Canny算子定位的邊緣點，然后利用Zernike 矩算法對可能的邊緣像素點進行正交復數矩計算，從而實現亞像素點的精確定位。

3.3 改進的Zernike矩邊緣檢測算法實現

本文通過Canny算子對齒輪圖像進行邊緣檢測，并保存所有可能的粗定位邊緣像素點。使用7×7模板，將模板系數與粗定位邊緣像素點做卷積運算，并通過式（7）求取邊緣參數k 、h、 l和θ。當粗定位邊緣像素點滿足Zernike矩邊緣點判斷條件k≥kt且l≤lt時，判斷該像素點為邊緣點，并通過式（8）進行精確計算，獲取亞像素級坐標。遍歷粗定位邊緣像素點即可得到亞像素邊緣。

4 齒輪參數的測量

4.1 齒輪基本參數的測量

（1）齒輪中心（x0，y0）

參照組使用傳統開胸手術方法，患者進行全身麻醉，在患者第5肋間進行消毒后[3]，做手術切口，在確定病灶位置后，將病灶切除，并清掃淋巴結，然后縫合患者傷口并消毒。實驗組使用微創手術方法，患者行靜脈復合全身麻醉，氣管插管，在患者的第4肋間做主操作孔，第8肋間建立輔助操作孔，第7肋間建立觀察孔，將患者病灶切除后，要清洗胸腔[4-7]，然后縫合傷口。

齒輪中心作為齒輪參數測量最基礎也是最重要的參數，其定位的準確度將直接影響后續齒輪參數測量的精度。經過多種方法比較，本文使用重心法進行求取。首先對齒輪的亞像素邊緣進行填充，再對填充的齒輪圖像進行連通區域標識，通過計算得到連通區域的重心點坐標，此坐標即為齒輪中心。

（2）齒頂圓半徑ra

本文采用凸包法求解齒頂圓半徑，通過凸包算法在齒輪亞像素邊緣輪廓外構建外凸包結構，將外輪廓的像素點全部包含在外凸包結構內。外輪廓與外凸包結構會產生多個交點，此時可將交點視為齒輪齒頂圓上的像素點，計算交點到齒輪中心的距離并取平均值，即為齒頂圓半徑。凸包結構圖如圖6所示。

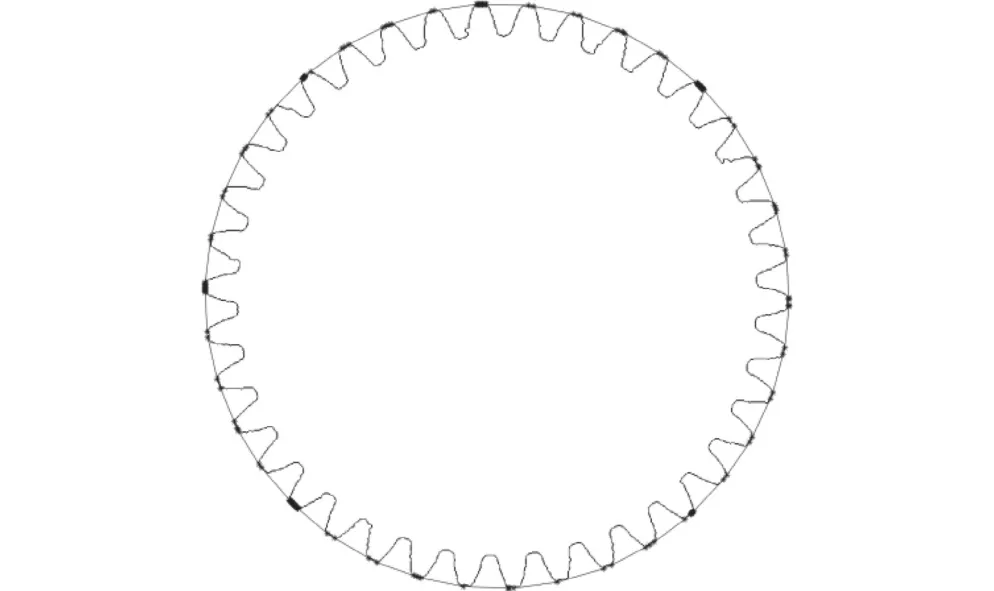
圖6 凸包結構圖

（3）齒根圓半徑rf

求解齒根圓半徑需要先求解出齒輪外輪廓到齒輪中心的距離，此時，齒輪外輪廓到齒輪中心的距離最小的點及其周圍輪廓點可視為齒根圓上的點，將得到的距離最小的40個點視作齒根圓上的點，計算這些點到齒輪中心的距離并取平均值，即為齒根圓半徑。

（4）齒數z

本文使用統計連通域法實現齒輪齒數的快速測量，在獲得齒頂圓和齒根圓的半徑后，以齒輪中心為原點，以二者的平均值為半徑畫圓，以此設計掩模模板，在掩膜中將圓內部灰度值設為255；通過將掩膜與填充后的齒輪圖像相乘，獲取代表齒牙的連通區域；最后統計連通區域的個數，即可得到齒輪的齒數。掩膜結果如圖7所示。

圖7 掩膜處理后的連通域

（5）模數m、分度圓半徑r

本文通過已測得的齒輪參數來求取齒輪模數和分度圓半徑。齒輪模數m計算公式如式（9）所示，式中齒頂高系數取1。分度圓半徑r計算公式如下。

4.2 齒距偏差的測量

求解齒距偏差需要求解齒輪的基本參數，求解齒輪齒距偏差的流程圖如圖8所示。

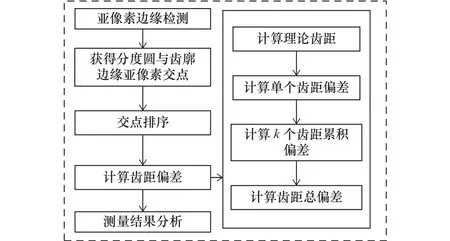
圖8 齒距偏差測量流程圖

本文利用機器視覺測量齒輪的齒距偏差，通過將分度圓與齒輪輪廓相交得到的交點作為依據進行分析，可以實現齒距偏差的精確計算。齒距偏差主要3個衡量方法，分別為單個齒距偏差Δfpt，k個齒距累積偏差Δfpk和距累積總偏差ΔFpk。其算法設計如下：

（1）設定兩幅大小為m×n，背景灰度值為255圖片picture1、picture2。在圖片picture1中，搜索齒輪輪廓的點，并把輪廓點灰度值設為50；在picture2中，以齒輪中心為圓心畫分度圓，并把分度圓點的灰度值設為100，picture1和picture2相加，遍歷灰度值為150的點，這些點就是分度圓和齒輪亞像素邊緣的交點,并將這些點按順時針順序標記為p1,p2,… ,p2k(z為齒輪齒數)。交點順序如圖9所示。

圖9 交點順序

（2）以p1為起始點，求出與其相鄰的同側齒廓的交點p3和圓心之間的角度∠p1op3。

設兩交點的坐標為（x1，y1）,（x3，y3）,由平面旋轉矩陣原理可得

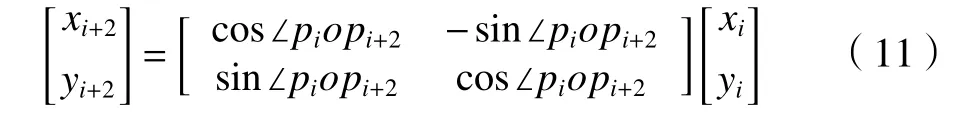
兩交點之間距離和夾角為

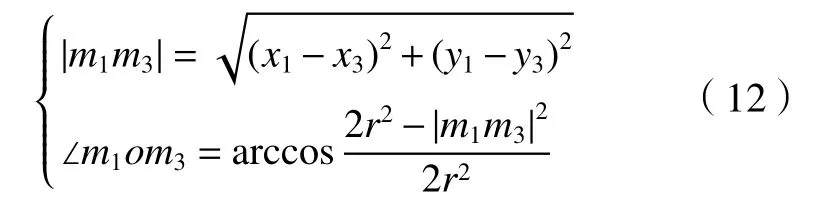
由此可得任意兩交點ma、mb間的夾角為

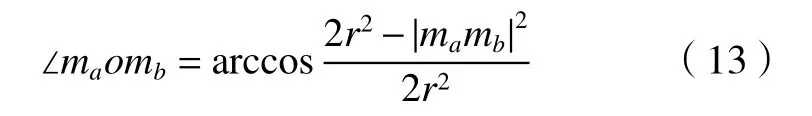
（3）計算兩交點理論齒距p，可得

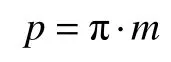
（4）求出對應的齒距偏差。

計算單個齒距偏差 Δfpi，得

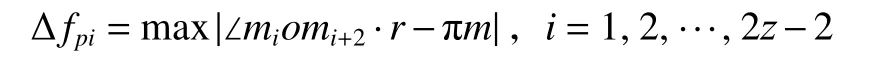
計算k個齒距累積偏差Δfpk，得

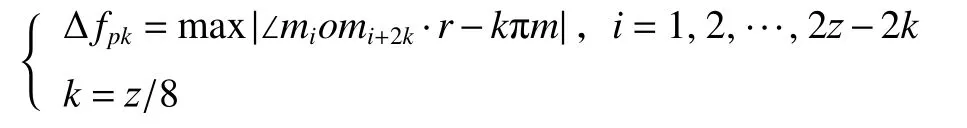
計算齒距累積總偏差ΔFpk，得

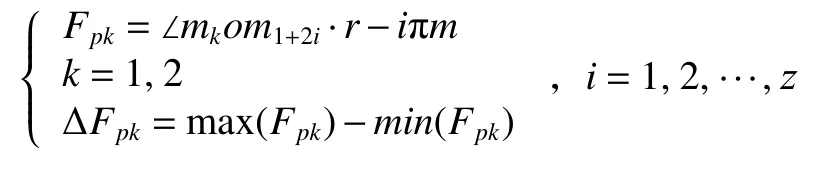
5 實驗結果與分析

為了驗證基于機器視覺的直齒輪齒距偏差測量方法的準確性，本文使用齒頂圓直徑為120 mm，模數m=3 mm，齒數z=38的直齒圓柱標準齒輪作為實驗對象。

5.1 齒輪基本參數測量

設計程序實現前述的算法，并分別使用本文算法和人工測量完成齒輪參數測量，并對測量結果進行比較和分析，人工測量如圖10所示，測量結果如表1所示。

圖10 人工測量

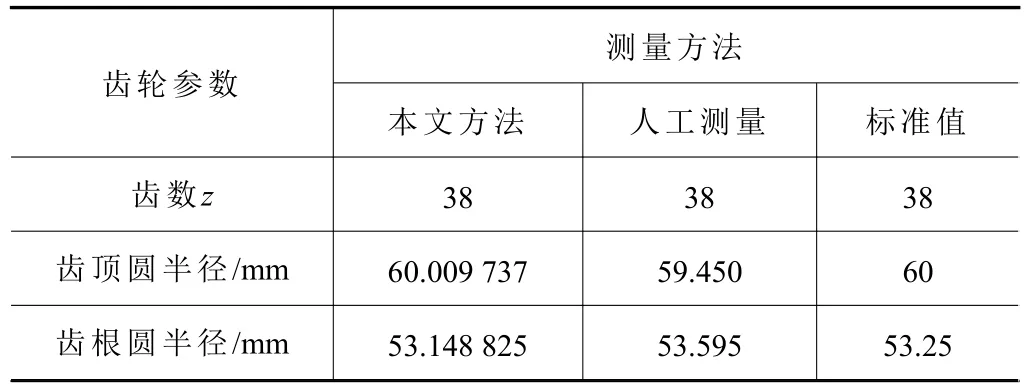
表1 實際尺寸與測量尺寸結果

對比本文算法和人工測量的齒頂圓、齒根圓半徑值。本文算法精確度高于人工測量，且誤差在0.02%以內，可以滿足實際測量需求。

5.2 齒距偏差測量

由前述齒距偏差測量方法，對單個齒距偏差和任意k個齒距累積偏差進行了測量，由前述可得，本系統像素當量：K=0.018 mm/pixel=18 μm/pixel。由表2可知，最大單個齒距偏差為11.81 μm。

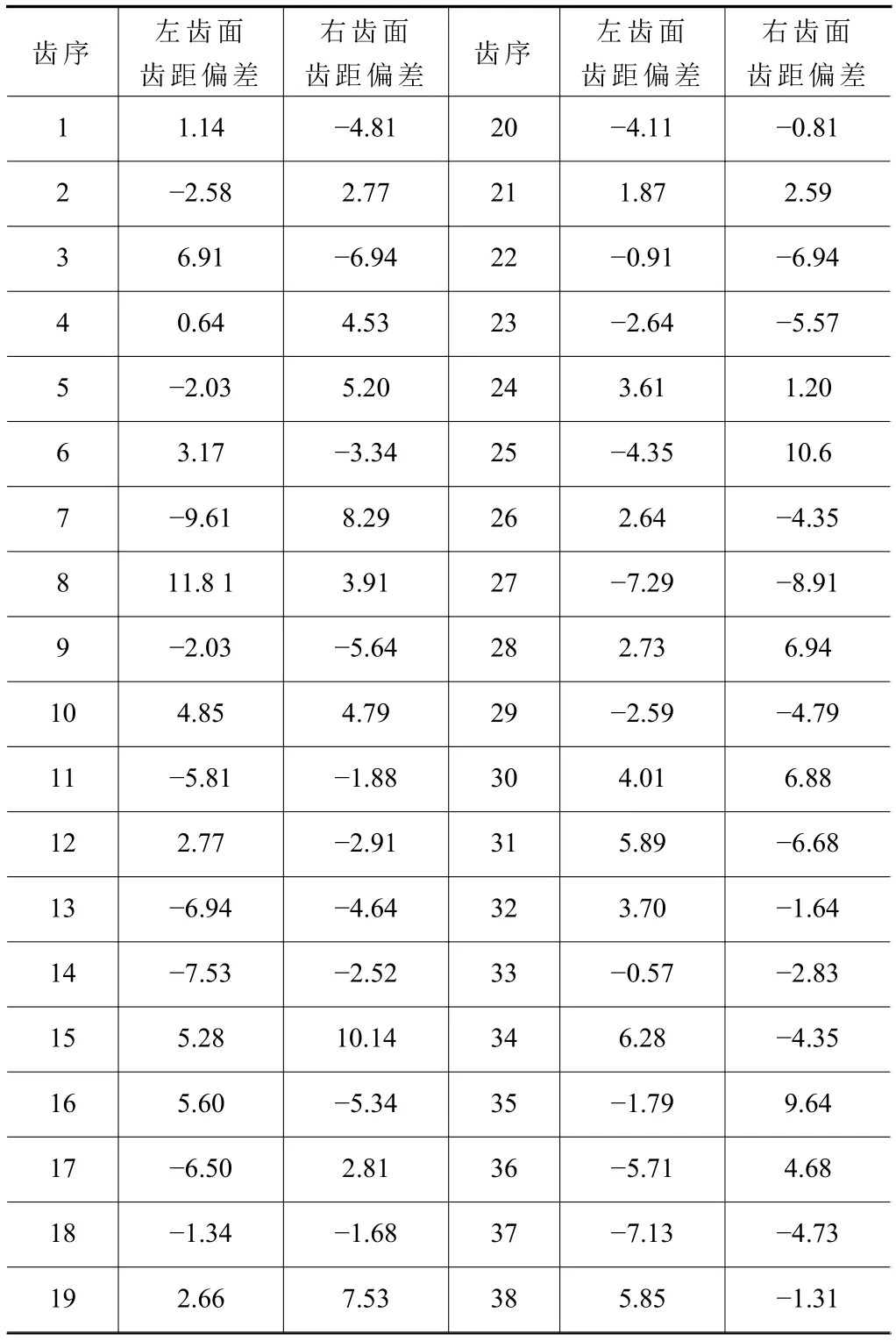
表2 任意單個齒距偏差測量結果 μm

如圖11所示，折線分別代表左齒面和右齒面的k個齒距累積偏差的測量結果，由于k值取小于z/8的最大整數，本文取k=4。由圖可知，左齒面最大k個齒距累積偏差23 μm，右齒面最大k個齒距偏差17 μm。齒距累積總偏差21.05 μm。各項偏差的最大值都在合理范圍之內。

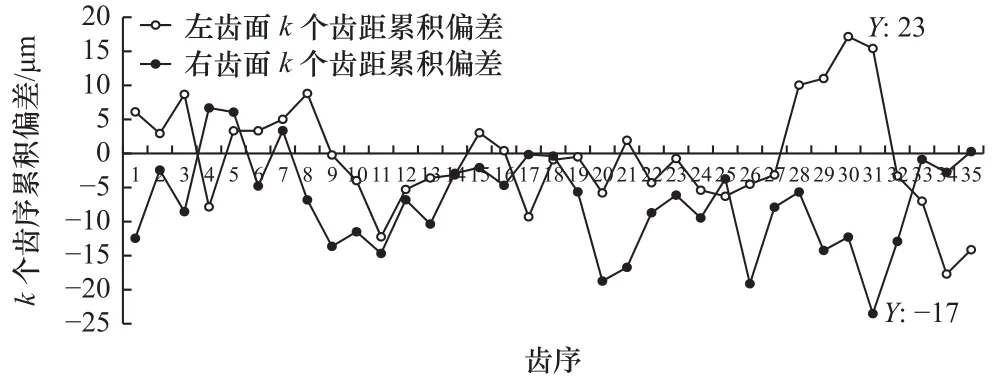
圖11 k個齒距累積偏差

6 結語

本文采用于機器視覺檢測方法對齒距偏差進行檢測，并通過直齒輪（齒頂圓直徑為120 mm，模數m=3 mm，齒數z=38）進行了實驗驗證。實驗表明，齒頂圓和齒根圓直徑的最大誤差小于0.02%，左齒面最大單個齒距偏差為11.81 μm，右齒面最大單個齒距偏差為10.6 μm。k個齒距累積偏差和齒距累積總偏差均滿足6級精度等級。在后續的研究當中，還需要進一步研究齒輪的其他幾何特征精密測量方法，提高綜合應用性。