有色信源卷積混合盲源分離算法*

莫海歌，胡顯智，戴旭初

（中國科學技術大學，安徽 合肥 230026）

0 引言

盲源分離是指僅根據(jù)觀測信號，利用信源和混合矩陣的部分先驗信息恢復出信源的信號處理技術，在通信信號處理[1-3]、音頻信號處理[4-5]、生物信號處理[6-7]等領域都具有廣泛的應用。根據(jù)混合方式的不同，盲源分離可分為瞬時混合信號的盲源分離和卷積混合信號的盲源分離，后者又被稱為盲解卷積。其中，瞬時混合指的是各個通道的觀測信號都僅由當前時刻的信源線性混合疊加而成，卷積混合則是各通道觀測信號由若干個不同時刻的信源線性混合疊加而成。在實際環(huán)境中，由于多徑效應，信號經(jīng)過反射、折射后會經(jīng)過不同路徑先后到達接收端。多個不同延時、不同方向的信號分量相互疊加就形成了卷積混合，這是十分常見的現(xiàn)象。因此，研究卷積混合盲源分離問題具有重要的現(xiàn)實意義。

目前求解卷積混合盲分離的方法主要分為頻域方法和時域方法兩類。頻域方法[8-10]的主要思路是利用短時傅里葉變換將信號轉換到時頻域，利用時域卷積等價于頻域乘積的性質，將卷積混合盲源分離問題變成求解若干個頻點的瞬時混合盲源分離問題。瞬時混合盲源分離固有的排序模糊性和幅度模糊性使得在各個頻點進行瞬時盲分離后不同頻點之間信源的順序和幅度可能不一致。排序不一致會導致無法得到一個信源的完整頻譜，從而無法逆變換到時域中。幅度不一致會導致信源在各個頻點處乘以未知的系數(shù)，等價于在時域上進行了未知濾波器的濾波，得到信源的濾波版本。目前使用獨立矢量分析（Independent Vector Analysis，IVA）[11]可以解決排序模糊問題，但幅度模糊問題無法徹底消除[12]。

時域方法則是在時域設計解混濾波器，將混合信號通過此濾波器后就可以得到信源的估計。大致有盲抽取[13]和先白化后分離[14-15]2 種思路。前者屬于“一步法”，利用高階統(tǒng)計量同時進行盲分離和盲解卷積，將獨立信源逐一抽取出來；后者屬于“兩步法”，先利用二階統(tǒng)計量進行盲解卷積，再利用高階統(tǒng)計量進行盲源分離。但是，這些方法都要求信源在時間上是獨立同分布的（即白色信源），不適用于時間上具有相關性的有色信源的情況。

文獻[16]提出了一種基于子空間的方法，利用子空間分解，將卷積混合模型轉化為瞬時混合模型進行求解。該方法可以用于有色信源，但是要求卷積混合多項式矩陣中每個列多項式矢量的階數(shù)相同且精確已知，同時該方法只有在高信噪比下才能獲得較好的分離性能。

利用信源有色特性對卷積混合多項式矩陣的作用機制，通過模型轉換，本文提出一種新的有色信源卷積混合盲源分離算法。該算法將有色信源的多通道卷積混合模型轉換為白色激勵源FIR 濾波器后，再進行卷積混合的級聯(lián)模型。根據(jù)這個轉換的等效模型，首先使用基于白化的方法求出白色激勵源以及等效的卷積混合多項式矩陣；其次估計出等效的卷積混合多項式矩陣中每列的最大公因式，該公因式即為FIR 濾波器估計；最后將估計的白色激勵源作用到估計的FIR 濾波器上，其響應即為原始有色信源的估計。相比于現(xiàn)有的方法，本文方法消除了卷積混合多項式矩陣中各個列多項式矢量的階數(shù)一致且已知的限制，不僅可以有效地分離有色信源，而且具有更好的抗噪聲性能。

1 信號模型和假設條件

1.1 信號模型

不失一般性地，考慮信源為有色源、傳輸通道為多通道FIR濾波器的多輸入多輸出（Multiple-Input Multiple-Output，MIMO）卷積混合的場景。假設信源個數(shù)為M，接收通道數(shù)為N，卷積階數(shù)為L，觀測信號為：

式中：s(k)=(s1(k),s2(k),…,sM(k))T是M×1維的有色信源向量；x(k)=(x1(k),x2(k),…,xN(k))T是N×1維的多通道觀測信號；Hl是第l個延時信源抽頭所對應的N×M維的傳輸矩陣；n(k)是N×1 維的觀測噪聲，且獨立于s(k)。

若使用多項式矩陣表示傳輸通道的傳遞函數(shù)，則信號模型（1）可表示為：

式中：H(z) 是關于z-1的多項式矩陣，

為了便于描述，本文稱H(z)為卷積混合多項式矩陣。

1.2 假設條件

對于信號模型（1）和（2），有如下的一些假設：

（1）N＞M；

（2）rank {H(z)}=M,?z≠0；

（3）{s(k)}是零均值、空間相互獨立的有色源信號矢量，即對于任意的i≠j，si(k)和sj(k)相互獨立；同時，對于任意的i=1,…,M，存在τ≠0，使得E[si(k+τ)si*(k)]≠0，上標“*”表示共軛運算。

特別地，根據(jù)平穩(wěn)隨機信號理論，si(k)可表示為平穩(wěn)白色源wi(k)激勵FIR 濾波器fi(k)的輸出信號，即si(k)=fi(k)wi(k)，用矢量形式可表示為：

式中：F(z)=diag{f1(z),…,fM(z)}是M×M的對角多項式矩陣，而且對于i≠j，fi(z)≠fj(z)；w(k)=(w1(k),…,wM(k))T是白色的激勵源矢量，即E{w(k+τ)wH(k)}=IMδ(τ)，IM表示M×M的單位矩陣。

（4）{n(k)}是零均值的高斯空時白噪聲，即E{n(k+τ)nH(k)}=σn2INδ(τ)。

卷積混合盲源分離的目標是在上述的假設條件下，從觀測信號x(k)中估計出有色信源s(k)，本文將通過基于白化的盲解卷積、信源有色特性估計、有色信源恢復等方法來實現(xiàn)這個目標。

2 基于白化的盲解卷積

2.1 信號模型轉換

將式（3）代入式（2），有：

需要指出的是，上述兩個觀察是本文設計算法的重要依據(jù)。

本節(jié)的后續(xù)部分將詳細介紹基于文獻[15]的白化盲解卷積的算法，以獲得信號模型（4）中白色信源w(k)和等效卷積混合多項式矩陣的估計。

2.2 解卷積多項式矩陣的結構

基于信號模型（4）和觀察1，文獻[15]表明，存在一個Le階的M×N的多項式矩陣G(z)，即：

使得

式中：IM是M×M的單位陣。

式（8）表明，存在一個多項式矩陣G(z)能夠消除信號模型（4）中對w(k)的卷積作用，故稱G(z)為“解卷積多項式矩陣”。因此，基于信號模型（4），從觀測到的卷積混合信號x(k)中分離出白色信源w(k)的關鍵是如何求解G(z)。

將式（5）和式（7）代入式（8），比較等式兩邊z-m項的系數(shù)矩陣，得到：

式中：當m-l＜0 或m-l＞Le時，Gm-l=0。將式（9）用矩陣的形式來表示，則有：

其中，

令(·)?表示偽逆運算，則式（10）可表示為：

則由式（7）、式（12）和式（13），有：

式（14）表明，解卷積多項式矩陣G(z)有特定的結構，它等于常數(shù)矩陣與一個多項式矩陣Ga(z)的乘積。另外，根據(jù)式（11）和式（13）可知，Ga(z)的系數(shù)矩陣也有特定的結構，而且由的系數(shù)矩陣唯一確定。下面將充分利用這些特定的結構，設計求解Ga(z)和的方法。

2.3 Ga(z)和的估計

2.3.1 Ga(z)的估計

根據(jù)式（13），估計Ga(z)的關鍵是估計SSH。令：

獲得了SSH的估計后，根據(jù)式（13），就可以直接得到多項式矩陣Ga(z)的估計。

在獲得Ga(z)的估計后，令：

綜合式（14）和式（20），可得到G(z)的估計為：

2.4 白色信源w(k)的估計

由于RH是滿秩的常數(shù)矩陣（未知），w(k)是白色源信號矢量，因此式（24）所表示的信號模型是一個典型的瞬時混合盲源分離模型，可以使用聯(lián)合近似對角化（Joint Approximate Diagonalization of Eigenmatrices，JADE）[17]、快速魯棒不動點獨立成分分析（Fast and Robust Fixed-Point Algorithms for Independent Component Analysis，F(xiàn)astICA）[18]等瞬時盲分離算法求出解混矩陣D，從而獲得w(k)的估計即：

式中：? (k)是分離后殘留噪聲；P是M×M的置換矩陣，表示排序的模糊性。特別地，利用功率歸一化，可以消除的幅度模糊性。

根據(jù)信號模型（4），以及w(k)具有白色特性、w(k)與n(k)的不相關性，有：

2.6 抗噪聲性能的改善

上述的白色信源w(k)和等效的多項式卷積混合矩陣的估計方法，都是基于式（8）的準則來設計的。很顯然，該準則沒有考慮噪聲的影響，因此可能會導致估計的中含有較大的噪聲分量? (k)，如式（25）所示。

從信道均衡的角度來看，式（8）的準則是“迫零準則”，其抗噪聲能力較弱。為了改善抗噪聲性能，考慮使用“MMSE 準則”來估計w(k)的延遲版本，d＞0。具體地，設計一個Le階的多項式矩陣Gd(z)，即：

使得

且滿足

利用正交原理，不難得到：

2.7 算法實現(xiàn)步驟

綜合上述討論和分析，基于白化的盲解卷積算法的具體實現(xiàn)步驟總結如下文所述。

式中：T 是樣本總數(shù)。

（3）利用式（13）估計濾波器Ga(z)的各階系數(shù)，并根據(jù)式（17）獲得vs(k)的估計。

（5）根據(jù)式（23）和式（24），計算y(k)，并且使用瞬時混合盲分離算法（如JADE 算法）對y(k)進行盲源分離，得到

（7）利用式（30），計算出多項式矩陣Gd(z)，并根據(jù)式（28）估計出

3 信源有色特性fi(z)的估計

3.1 求解近似公共零點的原理

設gj(z)的零點集合為Ωj={zj1,zj2,…,zjLj}，j=1,2,…,N，其中Lj是gj(z)的階數(shù)。

3.1.1 構造可能的近似公共零點的集合

應該注意到多項式gj(z)的階數(shù)可能是不同的，即Lj的大小不相等。不失一般性，假設g1(z)的階數(shù)最小，L1≤Lk，L1≤Lk。

首先，從Ω1中選取第1 個元素z11，以該元素作為種子來構造可能的近似公共零點集合Φ1，構造過程如下文所述。

（1）依次對Ω2,Ω3,…,ΩN中的每個元素計算它們與z11之間的歐式距離，從而找到每個集合中與z11最近的一個元素，即：

很明顯，集合Φ1,Φ2,…,都可能是公共零點集合。

3.1.2 評估每個集合中元素的聚集度

由式（34）的定義可知，dp越小，表明Φk中元素在z平面上的幾何位置越靠近，聚集程度越高；反之，則聚集程度越低。

3.1.3 確定一組近似公共零點

理論上，公共零點集合對應的dp值應為0，非公共零點對應的dp值較大，但是由于噪聲和計算誤差等因素的影響，公共零點集合對應的dp值為一個較小的值。

3.2 求解近似公共零點的步驟

（2）根據(jù)式（32）及相關的原理，構造可能的近似公共零點的集合Φ1,Φ2,…,ΦL1；

4 有色信源的恢復

式中：P是M×M的置換矩陣。

5 仿真實驗及分析

本節(jié)通過仿真實驗驗證本文提出的算法的有效性，并與現(xiàn)有的兩類典型算法（白化算法[15]、子空間算法[16]）進行性能比較。相比于本文算法，白化算法沒有基于最大公因式提取的信源有色性fi(z)估計這個步驟。

實驗中的噪聲為高斯白噪聲，信噪比定義為：

采用歸一化均衡均方誤差（Normalized Equalization Mean-Square Error，NEMSE）[15]來評估盲源分離的性能。對于信源i，NEMSE 定義為：

式中：E[·]是指對獨立的100 次實驗結果進行平均。

5.1 實驗1：H(z)列矢量的階數(shù)相等時的性能對比

仿真實驗中，實驗參數(shù)設置如下：

（1）信源數(shù)M=2，觀測信號的數(shù)目N=3，樣本數(shù) T=10 000。

（2）卷積混合多項式H(z)為：

即H1(z)的兩個列矢量的階數(shù)相等，L=1。

（3）兩個有色信源是由概率分布為拉普拉斯分布的獨立同分布的兩個白色信源，經(jīng)過1 階的FIR 濾波器得到的，對角的多項式矩陣F(z)為：

（4）G(z)的階數(shù)Le=3；在求解近似公共零點的算法中，閾值ε=0.2；瞬時盲分離算法均選擇JADE算法；估計的算法中，設置延時d=1。

圖1 是真實有色信源和使用本文算法分離出的有色源的部分波形。比較圖1（a）和圖1（c）、圖1（b）和圖1（d）可知，在忽略幅度模糊的情況下，二者的波形十分相似，表明本文的算法能夠有效地分離出兩個有色信源。

圖1 真實信源和本文算法分離的信源波形

圖2 是3 種算法的NEMSE 隨信噪比變化的曲線。通過對比可知：白化算法的分離性能最差，特別是在SNR大于15 dB 后，NEMSE 出現(xiàn)了性能地板，這主要是白化算法要求信源必須是具有白色特性所致，表明白化算法不適合直接用于有色源的卷積混合盲分離；子空間算法的分離性能較好，且分離性能隨著信噪比的增大而逐漸提高；本文算法的分離性能最好，與子空間的算法相比，在信噪比為15～30 dB 時，NEMSE 有4～5 dB 的性能增益。

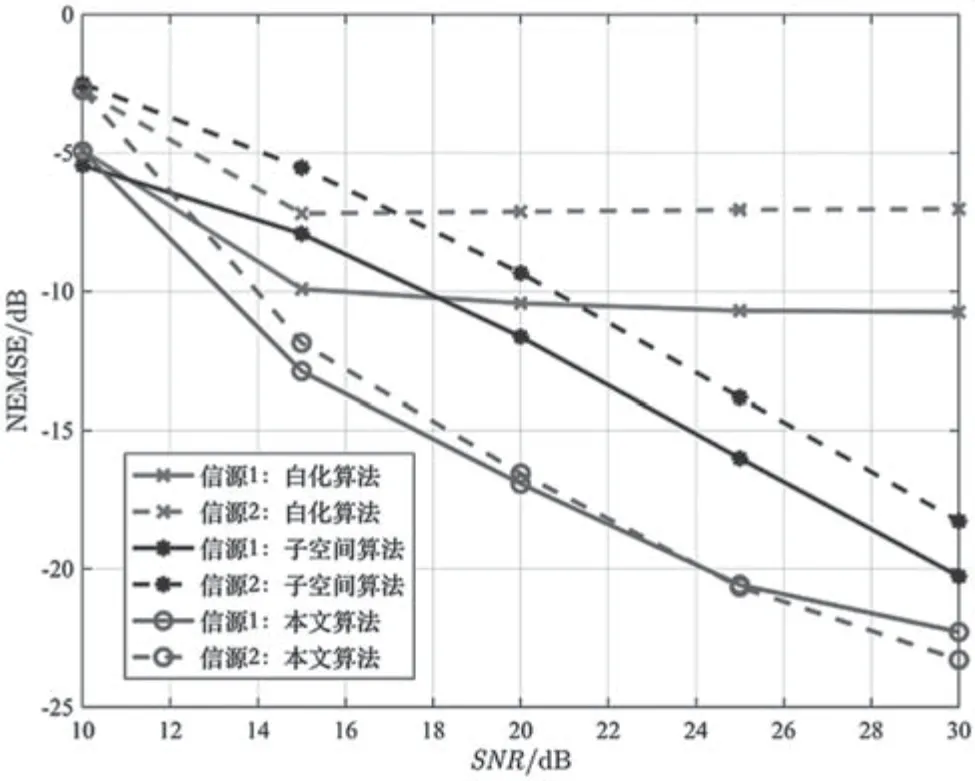
圖2 NEMSE－信噪比的關系曲線（H(z)=H1(z)）

5.2 實驗2：H(z)列矢量的階數(shù)不等時的性能對比

實驗2 與實驗1 的主要不同之處在于卷積混合多項式矩陣H(z)不同，即與信源1 和2 相對應的多項式列矢量的階數(shù)不同，分別為2 階、1 階，具體為：

圖3 NEMSE－信噪比的關系曲線（H(z)=H2(z)）

從圖3 可以看出，當兩個有色源所對應的卷積混合階數(shù)不等時，白化算法的性能與實驗1 基本相同，表明白化算法對不同有色源卷積階數(shù)的一致性不敏感，但總體性能表現(xiàn)較差；子空間算法的分離性能嚴重下降，特別是信源2 的分離性能最差，表明子空間算法對不同信源卷積混合的階數(shù)的一致性非常敏感，其主要原因是子空間算法要求卷積混合多項式矩陣的各階系數(shù)矩陣必須滿秩，而本實驗中的H2(z)顯然不滿足這個條件，因此導致算法的性能嚴重惡化；本文提出算法仍表現(xiàn)良好，能夠很好地適應卷積混合的階數(shù)不等的情況，而且抗噪聲的能力明顯優(yōu)于白化算法和子空間算法。

6 結語

本文通過對有色源建模、觀測信號的模型轉換，將有色源卷積混合盲分離問題分解為白色源卷積混合盲分離、列多項式矢量最大公因式提取兩個子問題，并詳細描述了求解兩個子問題的方法和步驟。仿真實驗結果表明，不論每個有色源卷積混合的階數(shù)是否相等，本文提出的算法都能有效進行分離，而且抗噪聲的性能也明顯優(yōu)于現(xiàn)有的其他算法。

另外，本文提出的算法已應用到某工程項目中，在不同的實際場景下進行了實驗測試，結果表明，本文算法性能穩(wěn)定，能夠適應實際環(huán)境的變化，具有很好的實際應用價值。