四分裂導線-間隔棒體系直流融冰時子導線不同步脫冰動力響應分析

祝 賀，王瑋琦,2，邢宏超,2，廖漢梁，陳 桓,2，武文韜,2，周月帥,2

(1.東北電力大學 建筑工程學院，吉林 吉林 132012；2.吉林省輸電工程安全與新技術實驗室，吉林 吉林 132000)

在我國南方地區冬季，低溫雨雪天氣會造成電網設備嚴重覆冰，大面積停電，給人民日常生活帶來巨大影響。目前冬季輸電線路覆冰已經成為威脅我國電網安全運行最嚴重的自然災害之一[1-2]。

目前采取的除冰方法已有30多種，但大多數除冰方法受實際操作難度及經濟效益的影響無法在輸電線路中應用。對于輸電線路除冰方法，采用直流融冰產生焦耳熱的方法是最為快遞有效的除冰方法。與其他除冰方式之間進行對比，直流融冰方法操作簡單便于維護，在安全方面對電網的影響較小[3-6]。

很多國內外學者對輸電導線覆冰脫落的動力響應進行了研究，王璋奇等[7-8]對輸電導線脫冰振動過程中的動張力進行實驗研究，分析了不同脫冰速度及不同脫冰方式下導線的動張力變化特性。黃新波等[9]通過建立多檔導線計算模型，對脫冰時導線的不平衡張力在脫冰方式及覆冰厚度等因素下，對導線脫冰不平衡張力進行分析。文獻[7-9]都是對覆冰導線在脫冰時的張力變化進行研究，分析不同脫冰方式下導線的動張力變化特性。

李宏男等[10]通過建立單導線試驗模型，采取質量塊等效代替覆冰模擬，測量不同覆冰厚度、速度等工況下導線張力及跨中跳躍高度。Ji等[11]采用ADINA軟件中3D梁單元建立一種新型覆冰導線模型，并與其在冬季室外100 m檔距上進行的脫冰試驗數據進行對比分析，驗證了其提出新型模型的準確性。Jamaleddine等[12]在實驗室對長度為3.22 m的兩檔輸電導線縮尺模型進行模擬試驗，通過控制電磁鐵脫落方式模擬導線覆冰脫落，同時采用ADINA仿真分析軟件進行數值模擬，對導線脫冰后的跳躍高度進行分析。文獻[10-12]使用不同方法模擬覆冰進行實驗，對導線覆冰脫落后的動態響應進行計算。

伍川等[13]通過有限元仿真，建立不同型號導線模型，分析在不同覆冰厚度、檔距等工況下導線的跳躍高度。吳天寶等[14]通過ADINA軟件有限元仿真，分析不同覆冰厚度、脫冰位置、導線長度等工況下，覆冰導線脫冰后跳躍高度的影響。晏致濤等[15]在有限元仿真中，采用三自由度懸索單元，通過生死單元法模擬覆冰脫落，研究高差對導線跳躍高度的影響。Gao等[16]建立酒杯塔塔線體系，考慮初始張拉力作用，計算不同脫冰方式的導線脫冰跳躍高度。文獻[13-16]采用有限元分析軟件，分析覆冰導線在不同脫冰方式下的跳躍高度隨時間變化的情況。

沈國輝等[17]將分裂導線等效合成單導線進行計算，提出分裂導線與合成單導線覆冰脫落時的等效計算方法。董永星等[18]分析了六分裂導線-間隔棒體系中子導線間不同步脫冰時，分裂導線體系的跳躍高度、導線張力及扭轉角度。Huang等[19-20]進行導線脫冰的縮尺試驗與數值模擬結果進行對比驗證，對最大脫冰跳躍高度計算公式進行改進，模擬四分裂導線在不同扭矩作用下的扭轉特性。文獻[17-20]對分裂導線體系脫冰跳躍高度及扭轉角度進行研究。

以上研究都關注了導線在脫冰時的動力響應，分析不同導線型號、覆冰厚度、檔距等產生的影響，在導線覆冰脫落的過程中，未考慮融冰電流產生的影響。對分裂導線體系，相關學者在覆冰脫落過程中將分裂導線等效成單導線計算，忽略了各子導線間不同步脫冰現象，并對不同步脫冰時分裂導線體系整體的動力響應進行計算，但忽略了受間隔棒約束作用下各子導線的脫冰跳躍及橫向擺幅情況。在實際融冰操作過程中，分裂導線體系存在不同步脫冰現象，分裂導線體系脫冰時受間隔棒約束作用產生橫向擺幅，進而造成分裂導線體系發生扭轉。為此根據我國西南地區線路中最常使用的四分裂導線，利用ANSYS有限元軟件，對四分裂導線-間隔棒體系計算，分析不同子導線脫冰下導線的位移及扭轉角度，研究四分裂導線體系直流融冰時各子導線不同步脫冰動力響應。

1 四分裂導線-間隔棒體系直流融冰振動方程

四分裂導線在直流融冰過程中，由于融冰電流的作用，導線焦耳熱不斷產生，冰層不斷融化，導線受的荷載主要是覆冰荷載，對于動態導線體系結構，覆冰荷載和位移都是時間t的函數。

基于達朗貝爾原理，采用集中質量法將導線等效為N個集中質量點，每個質量點包含豎直、水平和扭轉這三個自由度，建立輸電線路導線直流融冰過程的動力學方程[21]，見式(1)

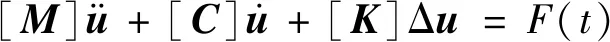
(1)

式(1)中的F(t)為動態冰荷載，隨直流融冰過程覆冰進行脫落從而變化，見式(2)

F(t)=[ρ導V導+ρ冰V冰(t)]g

(2)

式中，g為重力加速度，取9.8 m/s2。

2 四分裂導線-間隔棒體系直流融冰計算條件

根據實際直流融冰操作過程中經驗，對于分裂導線來說，存在脫冰不同步現象，分裂導線中子導線脫冰時間不一致，在實際融冰過程中無法做到全部導線同時進行覆冰脫落。本文考慮四分裂導線-間隔棒體系直流融冰時，不同子導線覆冰脫落時的跳躍分析，參考蔣興良等[22]在湖南雪峰山直流融冰試驗中，觀察記錄導線直流融冰時大部分導線覆冰在較短時間脫落的現象，為了解不同子導線脫冰時分裂導線體系中各子導線的動力響應，子導線均按100%脫冰率進行計算。

在有限元建模過程中，結合南方電網實際運行參數，對輸電線路和脫冰參數進行確定，將輸電導線的檔距取為200 m，導線型號為LGJ-400/50，導線具體參數見表1。

表1 LGJ-400/50導線結構特性參數Tab.1 Structural characteristics of LGJ-400/50 conductor

本文選取覆冰工況為我國西南地區冬季較為常見的20 mm雨凇覆冰情況進行分析，在20 mm覆冰時，由DL/T 5511—2016《直流融冰系統設計技術規程》[23]計算LGJ-400/50導線臨界融冰電流，在臨界電流區間內，根據南方電網直流融冰操作經驗，計算1 000 A融冰電流對應融冰時間，計算結果見表2。

表2 直流融冰過程參數Tab.2 Dc melting process parameters of Dashe Line

對四分裂導線-間隔棒體系中對子導線進行編號，分別討論單根子導線脫冰、兩根子導線脫冰、三根子導線脫冰、四根子導線脫冰不同工況下，分裂導線體系的脫冰動力響應。具體子導線編號命名情況見圖1。

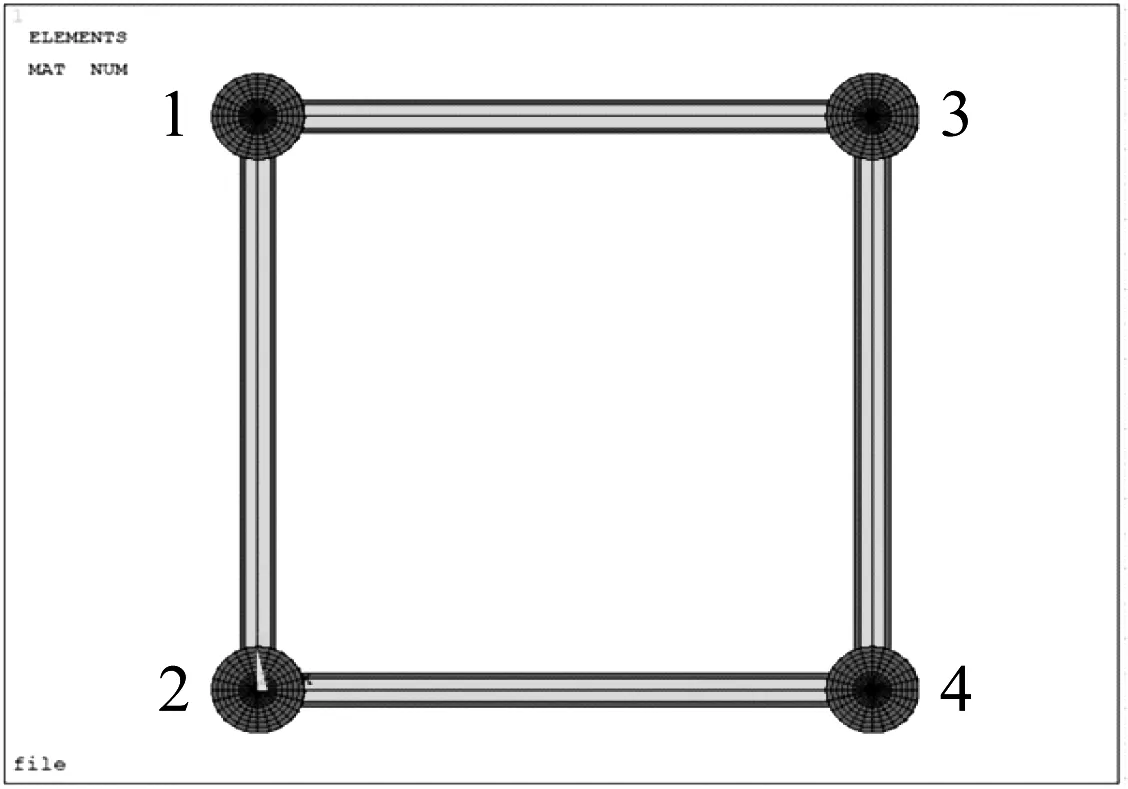
圖1 各子導線命名情況圖Fig.1 Diagram of sub-conductor naming

3 四分裂導線-間隔棒體系有限元模擬

3.1 四分裂導線-間隔棒體系有限元模型

由文獻[24]可知，對于輸電線路塔線體系來說，輸電塔的固有頻率要比輸電導線的固有頻率大很多，指出輸電線路塔線體系耦合效應對于輸電導線的脫冰動力響應的影響較小，可忽略不計。

四分裂導線-間隔棒體系建模過程中，間隔棒采用BEAM188單元，考慮間隔棒對導線之間的約束，間隔棒布置位置按照500 kV輸電線路實際工程情況進行布置。輸電線路中布置的LGJ-400/50四分裂導線，采用JZFD4-45400型間隔棒，各子導線之間間距為450 mm，該間隔棒由鋁合金制成重量為7.5 kg，在有限元計算中，對間隔棒建模采用等效建模方式。計算將間隔棒總重平均分配到四根等效圓棒上，通過已知的間隔棒重量及鋁合金密度，計算得出等效圓棒的截面半徑尺寸，通過鉸接方式與導線進行連接，間隔棒布置方式見圖2。

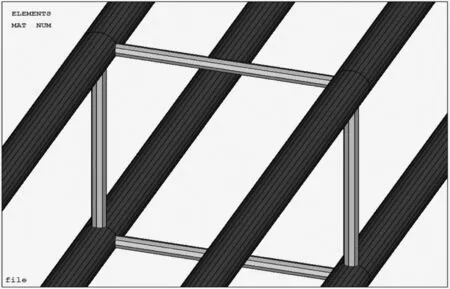
圖2 四分裂導線-間隔棒體系有限元模型圖Fig.2 Finite element model of quad bundle conductor spacer system

四分裂導線采用SOLID45單元進行模擬，采用SOLID45單元為了更好的模擬實際融冰過程中導線的情況，比以往采用LINK10單元建模時的模擬計算精度更加準確，充分保證了導線截面內部節點位移，在融冰電流作用下能夠更好的反應出導線融冰時的具體狀態。冰單元采用SOLID45進行模擬，彈性模量取為107Pa[25]，通過ANSYS有限元軟件中布爾運算將其與鋼芯鋁絞線合為一體，使導線和冰之間共節點，不產生相對滑移，覆冰導線有限元模型見圖3。

圖3 覆冰導線有限元模型圖Fig.3 Finite element model of iced conductor

建模時通過將鋼芯、鋁線和冰層之間進行分層建模，更加接近于實際工程條件。分層建模方式見圖4，內部層為鋼芯層，中間層為鋁線層，最外層為冰層。圖4中網格單元均為六面體，且高度對稱，整體均勻分布，規則整齊，可大大提高計算速度及精度。將兩端位置作為導線懸掛點，在分裂導線體系兩端各子導線節點處施加三自由度約束作為邊界條件。

圖4 四分裂導線-間隔棒體系網格劃分圖Fig.4 Grid division diagram of quad bundle conductor spacer system

3.2 有限元模型準確性驗證

為驗證有限元模型的準確性，需要取以往直流融冰下導線的結果進行分析對比，實際直流融冰條件不易模擬，導致目前對直流融冰導線動態響應實驗數據較少。通過與Meng等[26]在武漢國家電網研究中心建立的等比例235 m檔距輸電導線脫冰動態特性試驗結果進行對比分析。試驗中通過等效重力法將覆冰質量計算，由實際沙袋重物進行覆冰等效，通過電動切割器控制懸掛重物鋼繩模擬覆冰脫落。

選取Meng等[26]試驗中的B-3工況進行驗證，數據對比圖見圖5。試驗中其檔距為235 m的LGJ-630/45鋼芯鋁絞線，覆冰厚度15 mm，單檔100%脫冰，通過在有限元軟件中按B-3工況建立完全一致計算模型，將導線兩端施加三自由度約束，采用布爾運算將冰層附加在導線上，通過生死單元法，殺死覆冰單元模擬覆冰脫落，計算時將導線平均劃分為100個單元，計算時間步長為0.05 s。

本文阻尼計算根據瑞利阻尼(Rayleigh)假設，阻尼矩陣[C]是質量矩陣[M]和剛度矩陣[K]的線性組合，見式(3)。

[C]=α[M]+β[K]

(3)

式中：α為質量阻尼系數；β為剛度阻尼系數，由式(4)，式(5)求得。

(4)

(5)

式中：ωi,ωj分別為導線的第i階和第j階的振動頻率，由ANSYS有限元軟件計算求得；ξi,ξj分別為導線的第i階和第j階的振型的阻尼比，覆冰導線阻尼比取值為臨界阻尼的10%[27]。

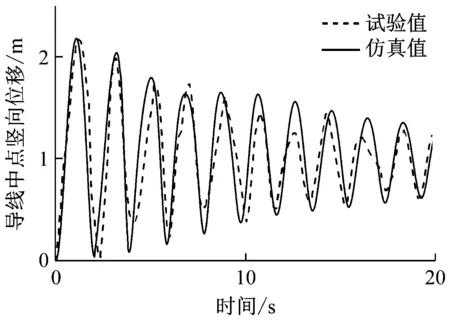
圖5 有限元數據與試驗數據對比圖Fig.5 Comparison between finite element data and test data

由圖5，本文采用SOLID45單元建模進行生死單元法模擬覆冰脫落的計算模型與Meng進行的脫冰試驗結果吻合較好，導線脫冰跳躍高度及趨勢保持一致，說明此方法模擬的準確性，為下文分析奠定基礎。

3.3 覆冰導線找形分析

首先設置單元類型和材料屬性，其次對實體單元施加一個較大的初應變值，設置較小的彈性模量并施加自重荷載，通過此方法可以節省時間并滿足高精度。同時基于找形分析法，以水平張力和弧垂對應關系為收斂條件進行迭代，最后得到覆冰導線在自重及覆冰荷載作用下的初始變形。找形完畢后進行重啟動分析，恢復覆冰導線的實際參數，設置材料實際應變。在ANSYS有限元軟件中對覆冰導線找形后數據進行提取，通過懸鏈線狀態方程[28]對理論值計算，與導線理論計算值進行對比分析，計算數據見表3。

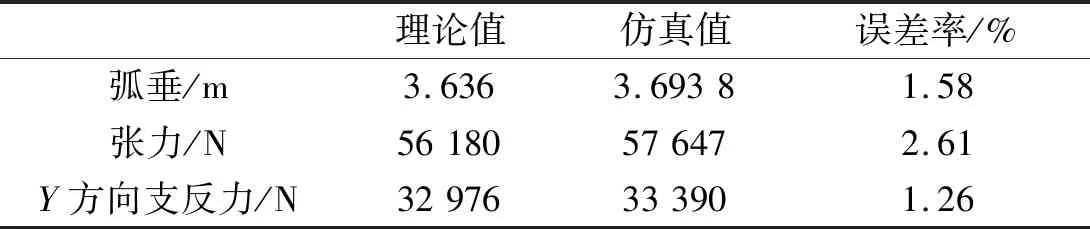
表3 導線找形數據對比分析Tab.3 Comparison and analysis of conductor shape finding data

3.4 覆冰導線預應力狀態下模態分析

覆冰導線在初始線形狀態下存在預應力，對分裂導線體系兩端施加三自由度約束，進行模態分析，繼而得到覆冰導線的頻率，可知結構剛度與變形快慢。圖6展示了四分裂導線-間隔棒體系前六階振型圖。

由振動理論，在結構振動過程中起主要作用的為較低階模態，高階模態對動力響應影響較小，并且衰減速度快，故只考慮低階頻率模態進行分析，調用有限元分析數據，表4為四分裂導線-間隔棒體系各階頻率及主要振型。

4 四分裂導線-間隔棒體系覆冰脫落響應分析

根據表2計算結果，同時結合南方電網實際操作過程中融冰經驗，在有限元計算過程中對于LGJ-400/50導線直流融冰，單導線融冰電流采取1 000 A進行融冰，四分裂導線則應采取單導線融冰電流的四倍大小進行融冰。采用生死單元法，殺死覆冰單元模擬覆冰脫落。研究參數包括四分裂導線-間隔棒體系中四根子導線同時脫冰、單根子導線脫冰、兩根子導線脫冰、及三根子導線脫冰的情況。

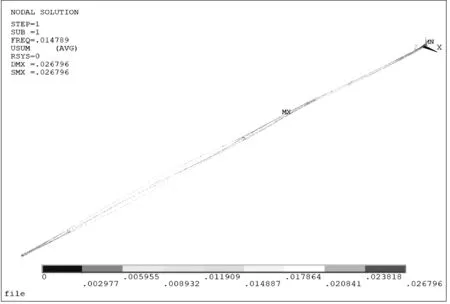
(a) 第一階振型

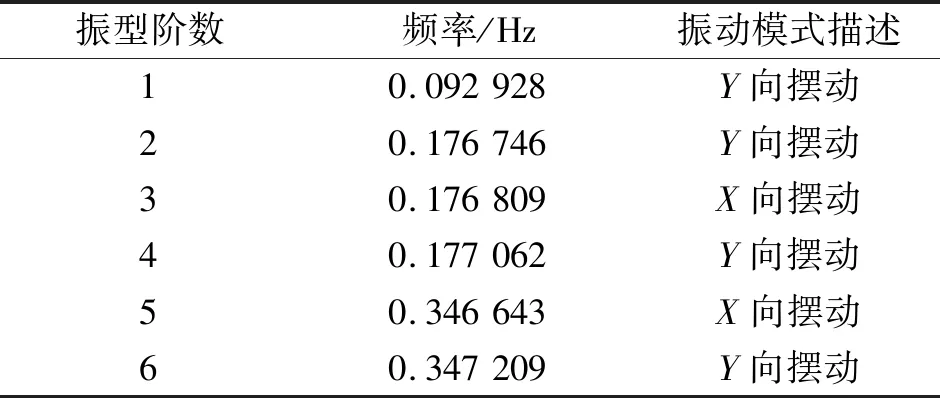
表4 導線六階模態固有頻率和振型描述Tab.4 Description of the sixth mode natural frequency and mode of the conductor

4.1 四根子導線同步脫冰分析

分析四根子導線同時脫冰下的動力響應，為更好的了解在融冰電流作用下導線脫冰的動力響應。考慮在自然狀態下無融冰電流、此覆冰條件下電網實際融冰電流1 000 A及規程計算最大融冰電流1 350 A，計算四根子導線的脫冰跳躍高度，由于四根子導線同步脫冰時，每根子導線的位移基本一致，相互之間無影響，故選取相同編號子導線中點脫冰跳躍高度，位移時程曲線見圖7。

圖7 不同融冰電流下導線中點豎向位移時程曲線Fig.7 Time-history curve of vertical displacement of midpoint of conductor under different melting current

表5為四根子導線同步脫冰時，在不同融冰電流作用下，導線最大跳躍高度位移及脫冰完成后穩定位置高度。

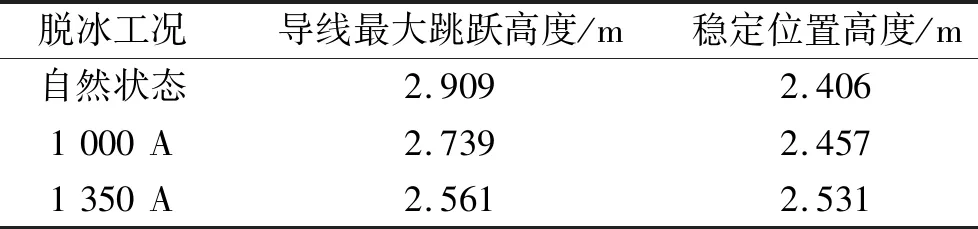
表5 不同工況導線脫冰跳躍值Tab.5 Deicing jump values of conductors under different working conditions

由圖8和表5，在相同覆冰厚度影響下，導線覆冰脫落時的跳躍高度隨融冰電流的增加而降低，同時融冰電流越大，導線覆冰脫落后穩定位置的位移越低，為更好的分析這一現象的產生，提取相同編號子導線中點在覆冰脫落時導線張力值，導線張力情況見表6。

表6 不同工況導線中點張力值Tab.6 Midpoint tension values of conductors under different working conditions

表6結果表明，在不同融冰電流的作用下，導線的水平張力會隨著融冰電流的增加而減小。在融冰電流的作用下，導線的結構發生變化，導線的線長隨融冰電流的增加而變長，進而導致覆冰脫落后穩定位置的位移降低，同時融冰電流越大，導致導線覆冰脫落后的跳躍高度降低。

4.2 單根子導線脫冰

分析單根子導線脫冰的影響時，由于四分裂導線-間隔棒體系為對稱結構，故選取2號子導線脫冰，其余三根子導線不脫冰進行研究分析。

圖8、9結果表明，在2號子導線脫冰時，2號子導線的豎向跳躍幅度最大，其余三根未脫冰子導線也發生跳躍現象，3號子導線的跳躍幅度最小，1號子導線的跳躍幅度最大。對于導線的橫向擺幅位移，各子導線橫向擺幅基本呈現對角線對稱趨勢，脫冰的2號子導線橫向擺幅較小，與對角線未脫冰3號子導線橫向擺幅基本一致，未脫冰的1號子導線與4號子導線的橫向擺幅較大，橫向最大擺幅位移達到0.3 m。

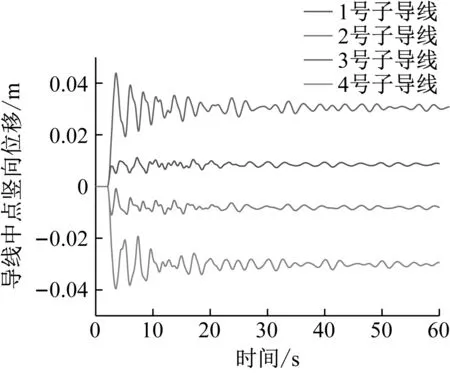
圖8 單根子導線脫冰時各子導線中點橫向擺幅位移時程Fig.8 Lateral swing displacement time history of midpoint of each sub-conductor during deicing of single sub-conductor

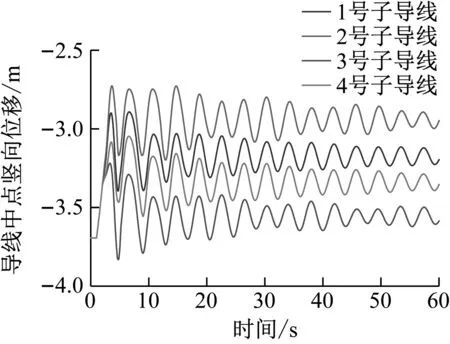
圖9 單根子導線脫冰時各子導線中點豎向跳躍位移時程Fig.9 Vertical jump displacement time history of midpoints of each sub-conductor during deicing of single sub-conductor

圖10為單根子導線脫冰時，四分裂導線-間隔棒體系的扭轉角度時程，結果表明扭轉角最大達到13.6°，當脫冰完成四分裂導線-間隔棒體系整體扭轉9.8°。

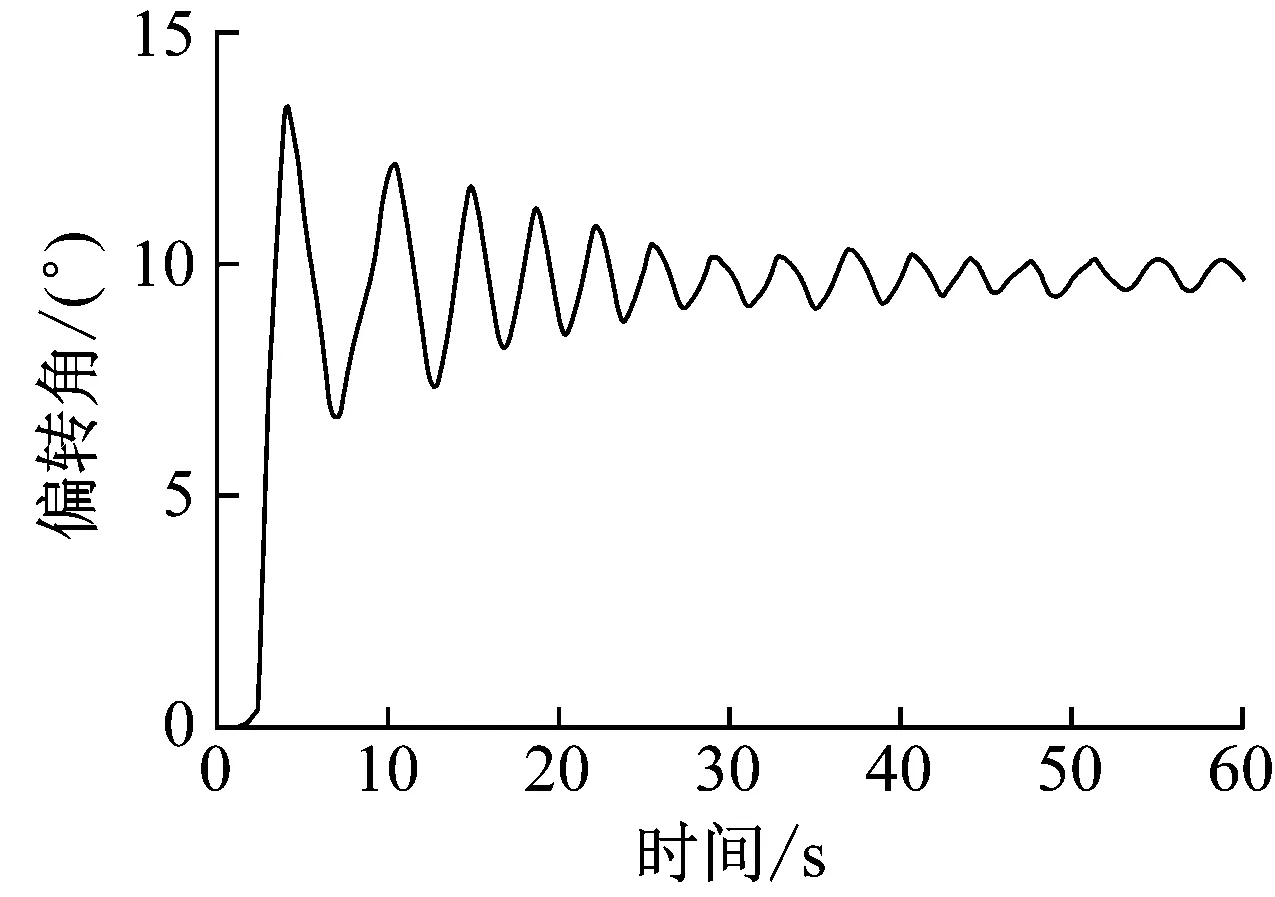
圖10 單根子導線脫冰時分裂導線體系扭轉角時程Fig.10 Torsional angle time history of split conductor system during deicing of single sub-conductor

4.3 兩根子導線同步脫冰分析

分析兩根子導線脫冰時，存在三種情況的脫冰方式，分別為對角線兩根子導線脫冰，上端兩根子導線脫冰，下端兩根子導線脫冰。

4.3.1 對角線子導線同步脫冰分析

選取1號子導線與4號子導線兩根在同一對角線上子導線進行脫冰，在對角線兩根子導線同步脫冰時，對四分裂導線-間隔棒體系不同子導線情況進行分析。

圖11、圖12、圖13結果表明，對角線子導線同時覆冰脫落時，1號子導線與4號子導線的橫向擺幅的位移基本呈對稱趨勢，在同一對角線上的未脫冰的2、3號導線橫向擺幅的位移趨勢相同，最大橫向擺幅的位移僅為5×10-4m。脫冰的1、4號導線豎向跳躍高度位移與未脫冰導線振動趨勢相同，分裂導線體系偏轉角度較小，子導線呈現同步振動跳躍現象。

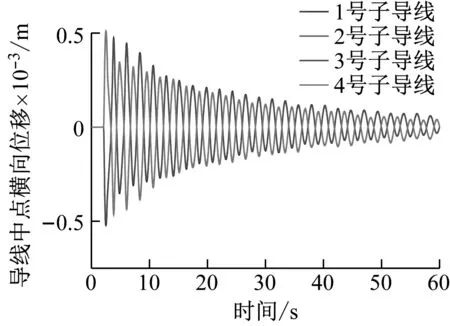
圖11 對角線子導線脫冰時各子導線中點橫向擺幅位移時程Fig.11 Lateral swing displacement time history of the midpoint of each sub-conductor during deicing of diagonal sub-conductor

圖12 對角線子導線脫冰時各子導線中點豎向跳躍位移時程Fig.12 Vertical jump displacement time history of the midpoint of each sub-conductor during deicing of diagonal sub-conductor

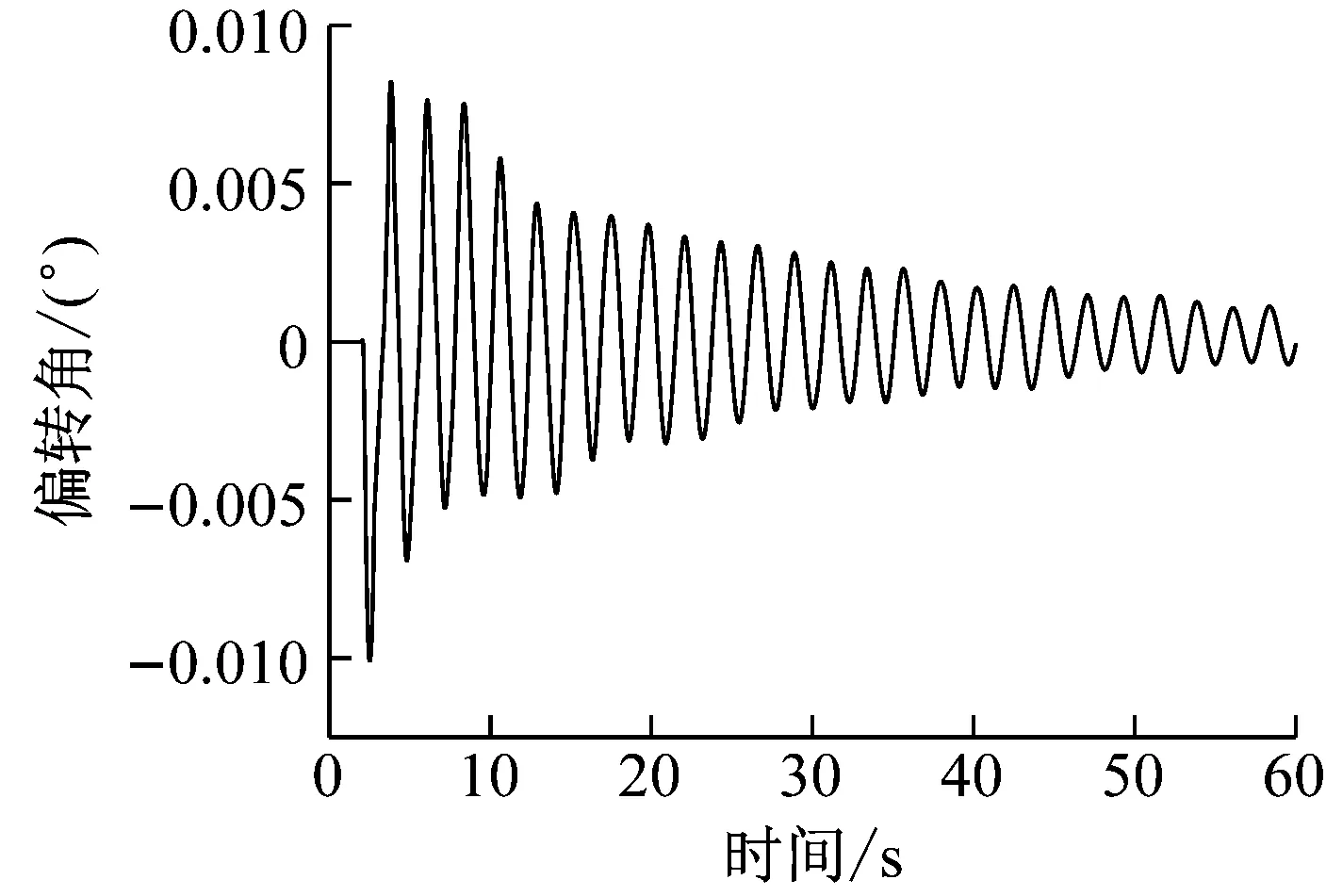
圖13 對角線子導線脫冰時分裂導線體系扭轉角時程Fig.13 Torsional angle history of split conductor system during deicing of diagonal sub-conductor

4.3.2 同側兩根子導線同步脫冰分析

選取3號子導線與4號子導線兩根在同一側上子導線進行脫冰，在同側兩根子導線同步脫冰時，對四分裂導線-間隔棒體系不同子導線情況進行分析。

圖14、圖15、圖16結果表明，在3、4號同側子導線脫冰時，其橫向擺幅的位移比未脫冰的1、2號子導線小，豎向跳躍的位移比未脫冰的1、2號子導線大，分裂導線體系的扭轉角度最大達到16.3°。在同側子導線脫冰時，分裂導線體系一側的重量下降，在間隔棒約束的作用下，分裂導線體系整體向脫冰一側扭轉。

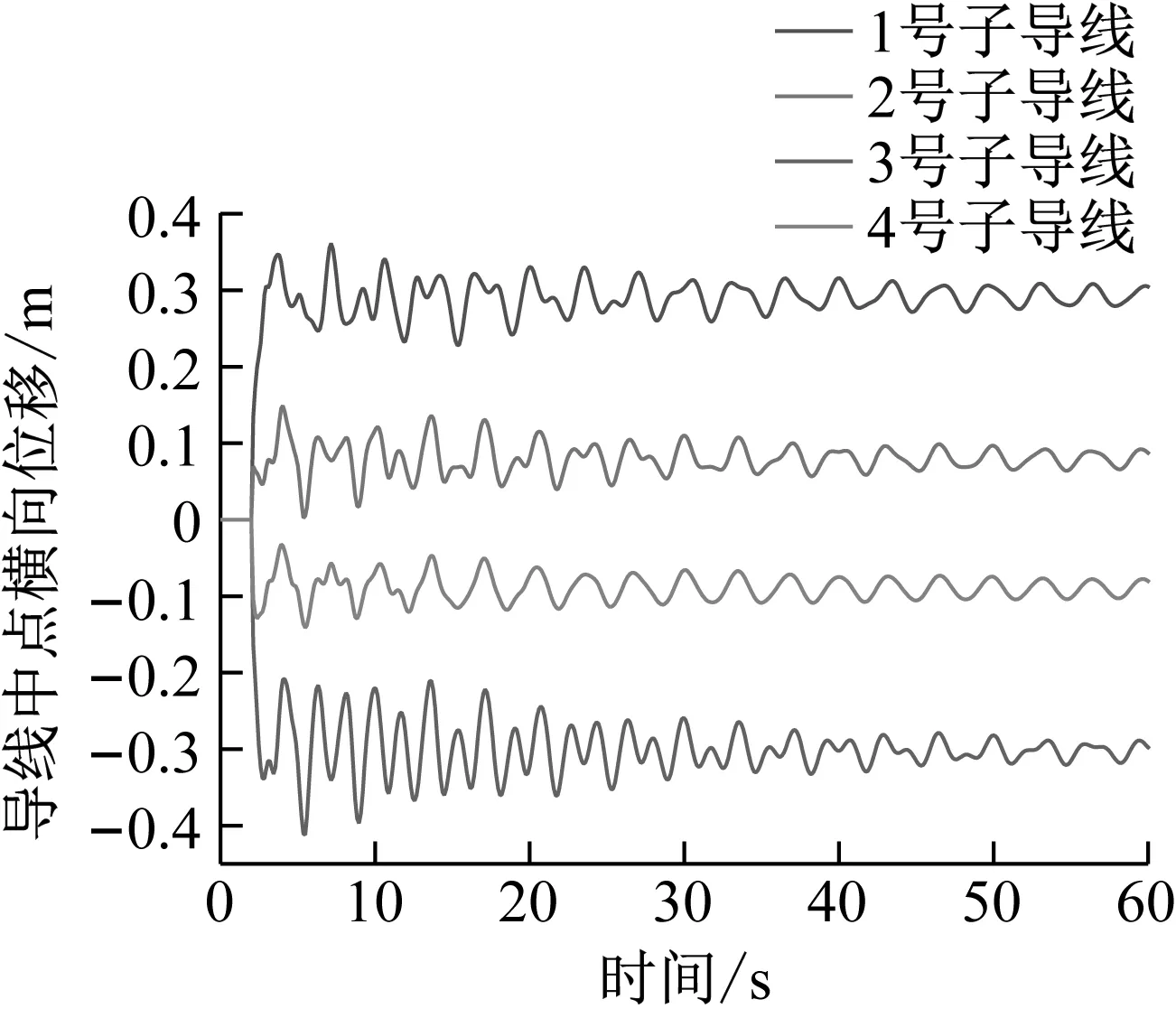
圖14 同側子導線脫冰時各子導線中點橫向擺幅位移時程Fig.14 Lateral swing displacement time history of midpoint of each sub-conductor during deicing of same side sub-conductor

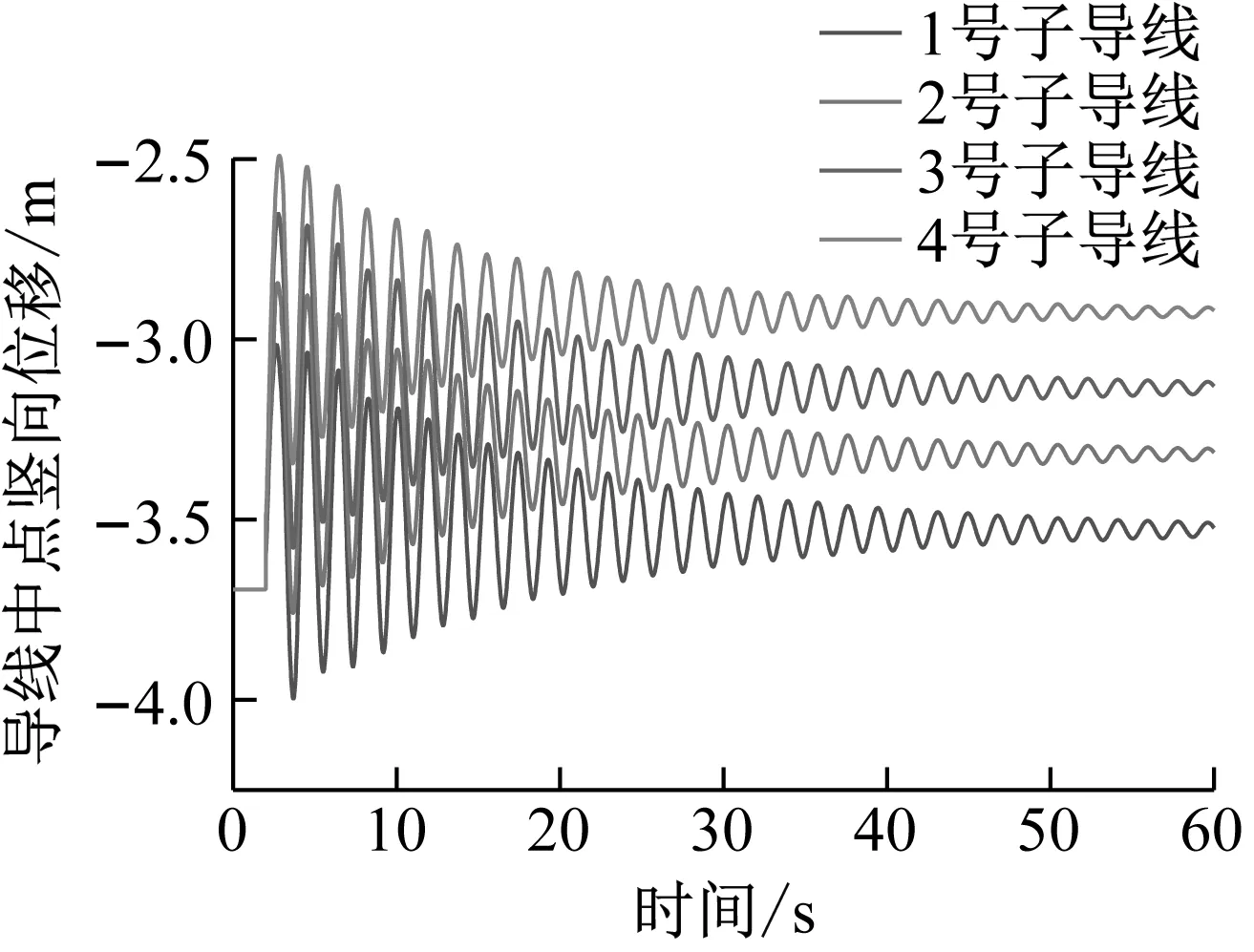
圖15 同側子導線脫冰時各子導線中點豎向跳躍位移時程Fig.15 Time history of vertical jump displacement of midpoint of each sub-conductor during deicing of same side sub-conductor

圖16 同側子導線脫冰時分裂導線體系扭轉角時程Fig.16 Torsional Angle time history of split conductor system during deicing of same side sub-conductor

4.3.3 下方兩根子導線同步脫冰分析

選取2號子導線與4號子導線兩根在分裂導線體系中下方子導線進行脫冰，對四分裂導線-間隔棒體系不同子導線情況進行分析。

圖17、圖18、圖19結果表明，分裂導線體系下方的2、4號子導線同時脫冰時，四根子導線的橫向擺動幅度較小，位移僅為5×10-4m。四根子導線的豎向跳躍趨勢保持一致，脫冰跳躍高度較大的為分裂導線體系中下側的3號子導線。在下方兩根子導線同步脫冰時，四分裂導線-間隔棒體系的扭轉最大角度為0.038°，扭轉角度較小，整體趨于穩定狀態。

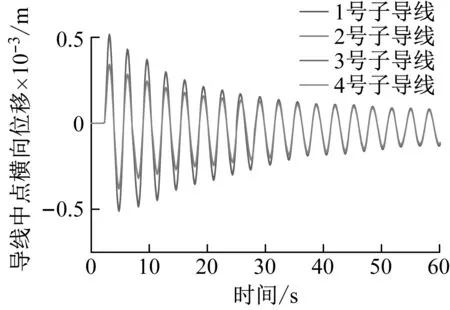
圖17 下方子導線脫冰時各子導線中點橫向擺幅位移時程Fig.17 Lateral swing displacement time history of midpoint of each sub-conductor during deicing of the lower sub-conductor

圖18 下方子導線脫冰時各子導線中點豎向跳躍位移時程Fig.18 Vertical jump displacement time history of the midpoints of each sub-conductor during deicing of the lower sub-conductor

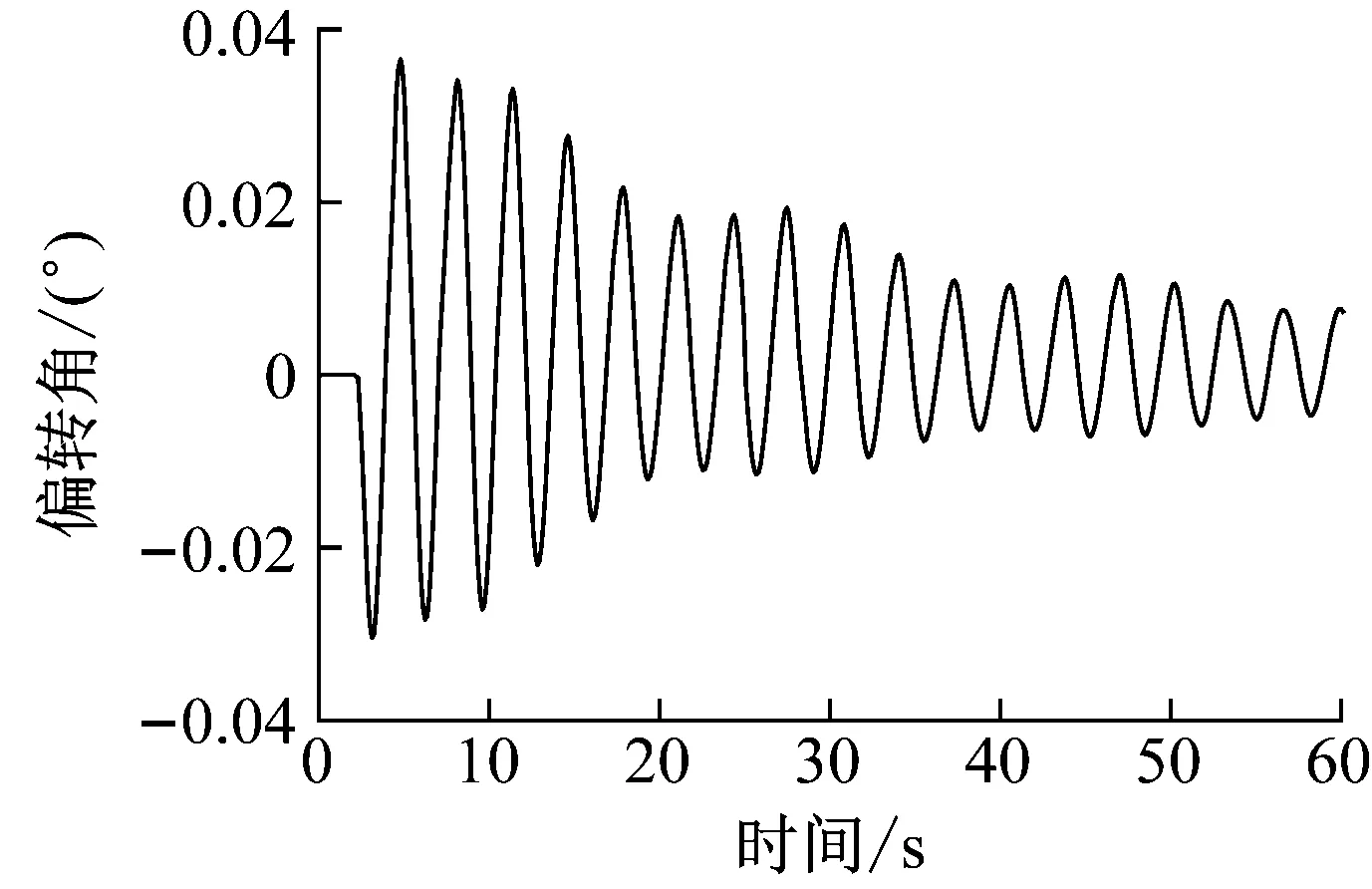
圖19 下方子導線脫冰時分裂導線體系扭轉角時程Fig.19 Torsional angle time history of split conductor system during deicing of lower sub-conductor

4.4 三根子導線同步脫冰分析

選取1、3、4號子導線脫冰進行研究，對四分裂導線-間隔棒體系不同子導線情況進行分析。

圖20、圖21、圖22結果表明，未脫冰2號子導線的橫向擺幅的位移，與其他三根脫冰導線比幅度較大，最大可達0.17 m，分裂導線體系橫向擺幅受間隔棒作用相互約束，對角線上子導線間橫向擺幅基本呈對稱趨勢。對于導線脫冰跳躍高度，未脫冰的2號子導線的脫冰跳躍高度的位移最小，4號脫冰導線位于四分裂導線-間隔棒體系下方，脫冰跳躍高度的位移最大。當三根子導線同步脫冰時，四分裂導線-間隔棒體系的扭轉最大達到12.8°，脫冰完成時，四分裂導線-間隔棒體系整體扭轉8.2°。

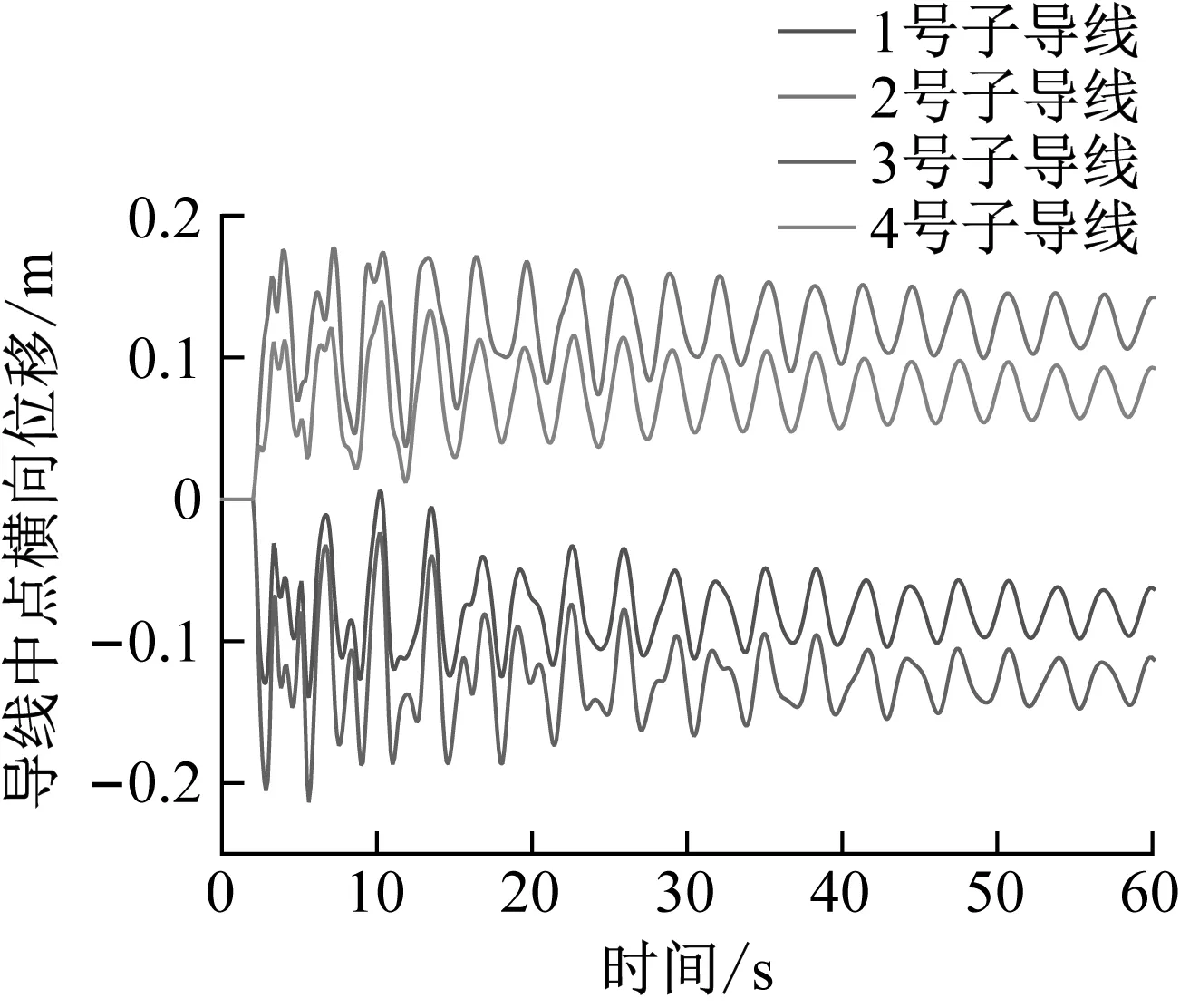
圖20 三根子導線脫冰時各子導線中點橫向擺幅位移時程Fig.20 Lateral swing displacement time history of the midpoint of each sub-conductor during the deicing of three sub-conductor

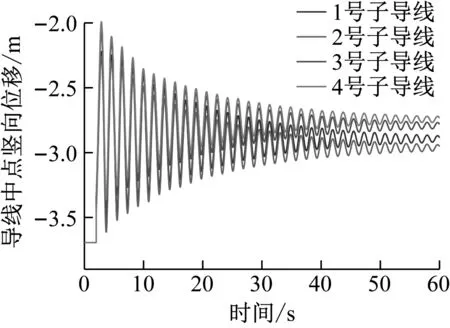
圖21 三根子導線脫冰時各子導線中點豎向跳躍位移時程Fig.21 Vertical jump displacement time history of the midpoints of each sub-conductor during deicing of three sub-conductor

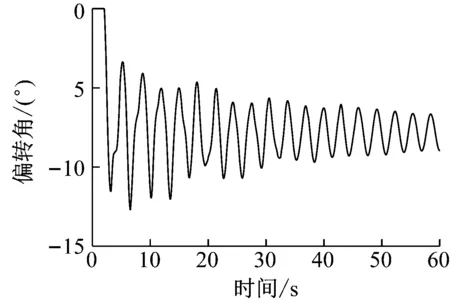
圖22 三根子導線脫冰時分裂導線體系扭轉角時程Fig.22 Torsional angle time history of split conductor system during deicing of three sub-conductor

4.5 計算結果分析

將本文計算結果與脫冰跳躍最大高度理論公式進行對比。目前我國輸電線路設計規程[29]中計算脫冰跳躍最大高度公式沿用前蘇聯的計算方法，見式(6)。

H=m(2-l/1 000)Δf

(6)

式中：l為檔距；Δf為覆冰導線脫冰前后弧垂差；m為考慮導線脫冰狀況引入的常量，整檔完全脫冰時取為1.0。

文獻[30]通過數值模擬，采用線性回歸法將計算結果進行擬合，總結出較短檔距下導線脫冰跳躍高度的計算簡化公式，見式(7)。

H=1.82Δf

(7)

根據規程公式(6)及簡化公式(7)，與文中有限元計算結果進行對比，分析四分裂導線體系中子導線不同步脫冰時，分裂導線體系穩定狀態下對角線子導線脫冰及下方子導線脫冰工況，結果對比見表7。

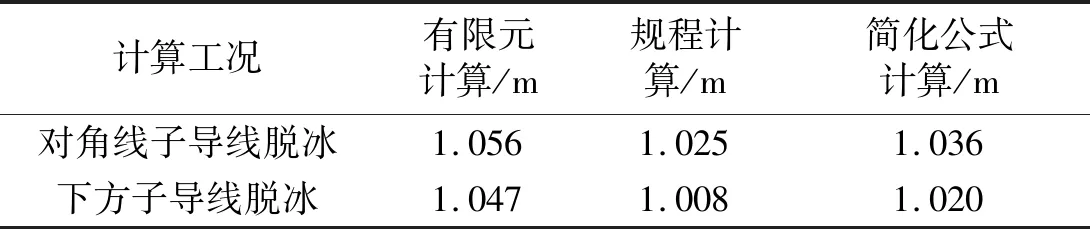
表7 分裂導線體系脫冰跳躍最大高度對比Tab.7 Comparison of maximum height of deicing jump in split conductor system

表7中結果表明，四分裂導線體系不同步脫冰時對角線子導線脫冰及下方子導線脫冰工況，文中有限元計算導線最大跳躍高度與規程及簡化理論公式結果相近，誤差率在4%以內。

5 結 論

本文采用ANSYS有限元軟件中LS-DYNA PrepPost模塊，進行非線性結構動力學分析，考慮實際導線情況，對導線進行分層建模，進行覆冰導線找形分析，施加融冰電流采用生死單元法模擬覆冰脫落，與現有文獻中的數據進行對比，驗證了該方法的可靠性，并得出以下結論：

(1) 對于SOLID實體單元導線找形分析，基于找形分析法，以水平張力和弧垂對應關系為收斂條件進行迭代計算，并與弦鏈線狀態方程理論計算結果進行對比，計算值與理論值誤差率在3%以內。

(2) 據相關規程，對導線臨界最小融冰電流及最大融冰電流進行計算，分析得出在融冰電流作用下，導線脫冰跳躍高度隨融冰電流增加而減小，導線脫冰后穩定位置隨融冰電流增加而變大。根據這些影響規律，對實際工程中的線路融冰操作提供相關操作依據。

(3) 四分裂導線-間隔棒體系不同步脫冰時，對角線兩根子導線同步脫冰及下側兩根子導線同步脫冰時，導線橫向擺動幅度位移較小，豎向跳躍高度一致，分裂導線體系脫冰時整體呈現穩定趨勢。在分裂導線實際融冰操作過程中，建議選擇對角線子導線及下側子導線同步融冰，避免導線覆冰脫落時，分裂導線體系發生扭轉現象。

(4) 當單根子導線、同側子導線脫冰及三根子導線同步脫冰時，分裂導線體系下方子導線豎向跳躍高度較上方子導線較大，同時各子導線間存在橫向擺動幅度大，導致分裂導線體系脫冰時發生扭轉，同側子導線脫冰時扭轉角度最大達到16.6°，脫冰過程中各子導線間易發生碰撞，增加導線磨損風險。