一種基于北斗解調秒的鎖相模型

羅畢錕，羅畢鋒

（電子科技大學 自動化工程學院，四川成都，611731）

0 引言

高精度時間頻率體系作為國家信息基礎設施，是國家戰略資源。世界主要發達國家都高度重視時頻體系建設。時間頻率關系到國家安全和關鍵經濟領域的主權和安全，因此世界各國，特別是主要發達國家，政府投入巨資研究開發相關技術，并不斷完善時間頻率體系建設，以求保持領先地位。

授時體系是一個國家時頻體系的基本技術支撐，為滿足不同的需求，發達國家各自都建成或正在建設完善通過電話、網絡、低頻時碼、長/短波電臺和衛星等交叉互補的授時系統。先進的空—陸結合的授時體系已經成為其龐大工業、經濟、軍事等發展不可或缺的高科技支撐。其中，衛星授時是時間頻率體系中最主要授時手段之一，其授時精度高、覆蓋地域范圍廣、且使用方便。

而我國現有的時間頻率設備大量的都是“即收即用”，無自主保持能力，或者采用“實時授時+設備內部晶振守時”，晶振存在頻率準確度和老化率差、時間累計誤差大的缺點，不具備長時間高精度的守時能力。

使用解調秒的晶振鎖相模型是一種使用北斗衛星的解調秒的高穩定性對晶振進行調相，以達到和標準的解調秒同步的模型，可提供高準確度的10MHz頻率信號輸出。

1 理論模型

■ 1.1 模型整體框圖

頻率同步系統是使用鎖相環實現的。鎖相環是一種能夠跟蹤輸入信號相位的閉環自動控制系統，廣泛應用于信號處理、時鐘同步、倍頻、頻率綜合等領域。它根據輸入信號和反饋信號的相位差來調整壓控振蕩器的輸出頻率，達到輸入信號頻率和輸出信號頻率相等，輸入信號和輸出信號保持恒定的相位差，從而達到鎖定的目的。

其中，時間間隔測量負責比較本秒和參考秒的相位差；卡爾曼濾波器能夠很好地控制環路相位校正的速度和精度；壓控振蕩器給出一個10M信號，一部份作為輸出，另一部分通過分頻產生本地PPS信號與參考秒進行相位比較。

當本秒與參考秒相位保持一個恒定的差值，輸入信號頻率和輸出信號頻率趨于相等，從而達到頻率鎖定的目的。

圖1 頻率同步原理框圖

■ 1.2 相差跟蹤模型

本模型利用北斗的解調秒信號具有長期穩定的特性作為參考標準，比對出與10MHz晶振分頻秒的相位誤差Δt（單位：s），采用Kalman濾波控制算法對Δt進行平滑濾波，利用準確度Δf/f=Δt/τ(τ是取樣間隔，這里τ=1)計算出OCXO的準確度，最后通過微調OCXO的壓控電壓實現頻率鎖定。

北斗衛星的授時秒信號的特性曲線如圖，可以看出衛星授時信號的長期特性是穩定的,可以用于OCXO的頻率校準。但是衛星授時信號的短期抖動性極大，約有5E-8量級。因此需要對北斗衛星的解調秒進行濾波后使用。

圖2 衛星解調秒信號的特性曲線

1.2.1 Kalman 濾波器原理

要利用衛星授時信號對OCXO快速校準必須進行濾波處理減小短期抖動。在本模型中，采用卡爾曼濾波算法。

Kalman濾波器是一種基于最小均方誤差準則的最優線性時域濾波，采用狀態空間的方法描述系統，算法采用遞推形式，無凈差。濾波算法不需要過去的全部觀測數據，僅僅根據前一次的估算值的最近一個觀測數據來估計當前值。

Kalman濾波算法的系統狀態描述方程：

式(1)中X為系統狀態，A和B為狀態轉移矩陣，k為時間系數，U為系統的已知輸入，W為過程噪聲向量。

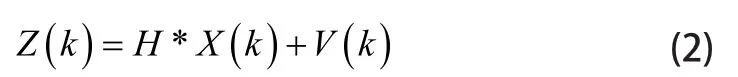
式(2)中Z是系統測試值，V是測量噪聲，H是線性連接矩陣。

圖3是Kalman濾波算法的基本步驟，P是系統狀態，X是對應的協方差，R為測量噪聲的協方差，Q為過程噪聲的協方差。

圖3 Kalman濾波器算法工作圖

1.2.2 Kalman 濾波器模型

本模型通過實時比對參考秒與60MHz信號的相位差，利用Kalman濾波算法輸出頻率控制量修正OCXO的頻偏。

OCXO的相位輸出模型為：

其中a是初始相位，b是頻率偏差，c是頻率漂移，?ξ1(t)是晶振的相位噪聲，?ξ2(t)是測量噪聲。

在此相位模型下有三個狀態參數，分別是相位、頻率以及頻漂，我們在Kalman濾波器中包括這三個參數，則系統的狀態方程為：

其中x1、x2及x3分別是相位、頻率和頻漂，輸入的測量值是參考秒與OCXO之間的相位，故測量矩陣為：

狀態方程可以表示為如下形式：

A是系統的狀態轉移矩陣,A

設定相位x1，頻率x2及頻漂x3的Kalman過程噪聲為及分別是相位白噪聲、頻率白噪聲和頻率游走噪聲的方差，此時測量噪聲協方差對于采用1pps信號測量而言，測試時間τ=1。

系統過程噪聲協方差矩陣此時可表示為：

σ1、σ2及σ3的取值如下：

式中hα是表征各種噪聲強弱的常數，α對應不同的噪聲類型（α=2對應白調相噪聲，α=0對應白調頻噪聲，α=-2對應隨機游動調頻噪聲）。

■1.3 PID控制模型

圖4 PID原理框圖

常見的數字PID控制方法有位置式和增量式，位置式PID算法每次輸出與整個過去狀態有關，計算式中要用到過去偏差的累加值，容易產生較大的累積誤差；而增量式PID只需計算增量，當存在計算誤差或精度不足時，對控制量計算的影響較小。

本模型采用了增量型PID控制算法，該算法數學模型如下：

?y(n)為n時刻輸出電壓的步進值，為比例增益，δ為比例帶，為積分系數，T為控制時間，TI為積分時間，稱為微分系數，TD為微分時間。

在本模型中，由于每次調節后OCXO都需要一定的時間使其輸出頻率穩定下來，即對它的控制具有較大的滯后性，并且由于對輸出頻率的調節精度和相位噪聲指標要求較高，所以每次頻率的拉動幅度不宜過大，并且拉動周期相應要長，即KP和KI不能過大，而KD可以相應的增大。

2 MATLAB仿真及實物驗證

■2.1 Kalman濾波器模型MATLAB仿真

我們利用MATLAB對上面的Kalman濾波器模型進行仿真，結果如圖5所示。

圖5 Kalman濾波器模型仿真結果

圖5中，上下較突出部分是原始數據，另一條是Kalman濾波器給出的預測值，可以明顯的看出經過Kalman濾波器后，數據相位抖動明顯減小，從仿真的結果看，前述模型能很好的滿足解調秒信號對晶振鎖相的需求。

■2.2 增量式PID控制模型MATLAB仿真

我們繼續利用MATLAB對PID控制模型進行仿真，結果如圖6所示。

圖6 增量式PID控制模型仿真結果

我們可以清楚的從仿真圖像上看出，通過該種增量式PID控制模型，系統對輸出的信號有非常明顯的收斂效果，可以清晰的發現輸出信號與標準時間的相位差可以快速的拉近并保持。

■ 2.3 實物驗證

我們將上述設計進行了實物生產與實際測試。在晶振鎖相過程中我們對其頻率準確度進行測量，鎖定曲線如圖7所示。

圖7 鎖定過程

晶振在進行充分預熱后，在經過20min的頻率鎖相時間后，本秒與參考秒的同步精度控制在100ns以內，進入鎖定狀態，準確度優于2E-10量級，如圖8所示。

圖8 晶振鎖相20min后的頻率準確度

經過24小時鎖相后的頻率平均準確度可以達到5 67E-14，如圖9所示。

3 結語

本文提出了一種利用Kalman濾波器對晶振輸出信號相位與北斗解調秒相位差進行處理后，使用增量式PID控制，對晶振的壓控端進行調節，從而實現對晶振的信號鎖相，提高晶振輸出信號的準確度的模型。該模型在MATLAB和實際實驗中均能使晶振在鎖相24小時后達到6E-14量級的頻率準確度指標，可以滿足無線基站、通信設備、時間基準、導航系統等無人值守環境下的晶振使用需求。

圖9 晶振鎖相24小時后的頻率準確度