基于振動信號多特征值的電力變壓器故障檢測研究

杜厚賢 劉 昊 雷龍武 仝 杰 黃建業 馬國明

基于振動信號多特征值的電力變壓器故障檢測研究

杜厚賢1劉 昊1雷龍武2仝 杰3黃建業2馬國明1

（1. 新能源電力系統國家重點實驗室（華北電力大學） 北京 102206 2. 國網福建省電力有限公司電力科學研究院 福州 350007 3. 中國電力科學研究院有限公司 北京 100192）

在基于振動的電力變壓器故障檢測領域，現有研究大多是針對某一特定型號或電壓等級變壓器開展的縱向比較，由此形成的診斷算法泛用性較差。為解決上述問題，該文提出了一種基于振動信號多特征值的電力變壓器故障檢測方法，搜集整理了不同電壓等級、不同型號變壓器正常與典型故障下的振動信號，統計了振動主頻分布情況，改進了100Hz占比、總諧波畸變率的計算式，分別將兩特征值的分類效果提高了79%、76%。提出了兩段式故障診斷流程，利用截斷正態分布擬合方法與合成少數類過采樣技術（SMOTE）對故障數據進行擴充，進一步提高了分類精度。測試結果表明，算法對正常、故障變壓器的識別準確度達到92.6%，適用于多變壓器的橫向診斷和對不同測點、不同工作狀態下數據的分類。

電力變壓器 振動 特征值 橫向診斷 兩段式診斷

0 引言

在變壓器故障檢測的諸多方法中，振動分析法以其檢測快速、對變壓器影響小、檢測精度高的優點，受到了國內外專家學者的廣泛關注[1-11]。變壓器在運行過程中，由于繞組受到周期性電磁力、鐵心的磁致伸縮[12-14]作用，將產生以100Hz為基頻，包含100Hz倍頻的振動信號[1-2]，當發生繞組變形、鐵心松動等故障時，于油箱壁測得的振動信號波形將發生改變，因此可通過分析變壓器的振動特征來反映其健康狀態[3]。河海大學馬宏忠等通過提取振動信號各頻段的能量，構造了由三個診斷特征組成的繞組變形診斷模型，檢測出兩臺測試變壓器的繞組變形故障并對比了二者故障的嚴重程度[4]；浙江大學熊衛華等使用希爾伯特-黃變換對變壓器正常和故障狀態下的振動信號進行分解，比較了變壓器故障時振動能量分布的變化情況[5]；西安交通大學汲勝昌等對變壓器的振動信號進行小波包分解，以分解后各頻段的能量構造特征矢量，分析了變壓器故障前后特征值變化情況[7]；華北電力大學劉云鵬課題組實地測量了162臺超、特高壓變壓器的聲紋特征，構造了主頻、振動熵等五個故障診斷特征值，通過劃定各特征值的預警閾值實現了對變壓器正常與不同故障工況的識別[8]；M. Bagheri等對變壓器鐵心繞組的振動特點進行了數學分析，通過機器學習方法開發了基于振動信號的變壓器運行狀態預測模型，實現了變壓器故障早期診斷[9]；C. Bartoletti等在分析變壓器振動特點的基礎上，提出了包含三個特征值的特征向量，在對新、舊、故障三類變壓器的區分上取得了良好效果[10]。

盡管上述研究取得了很大進展，但在實際應用中仍存在一些難以解決的問題：①現有研究大多是針對某一特定型號或電壓等級變壓器開展的縱向比較，由此形成的診斷算法難以推廣到其他型號或電壓等級的變壓器，泛用性較差；②在振動歷史數據缺失的情況下，基于時間域縱向對比的算法失效；③在診斷特征向量的構造上，目前廣泛使用“100Hz占比”、“總諧波畸變率（Total Harmonic Distortion, THD）”等診斷指標[8,10,15]，但變壓器正常運行時普遍存在的200Hz、300Hz等倍頻分量，將影響其診斷效果；④現場測量的變壓器大多處于正常工況，缺乏故障工況的振動數據，而在實驗室條件下人為設置故障，無法獲取足量的不同型號、不同電壓等級變壓器振動數據，數據的缺失與不平衡將嚴重影響算法的分類效果。

為了解決上述問題，本文提出一種基于振動信號多特征值的電力變壓器故障檢測方法，在搜集整理各電壓等級變壓器正常運行與繞組變形、鐵心松動、繞組松動、直流偏磁四類典型故障振動信號的基礎上，首先分析了變壓器正常運行時振動主頻的分布情況，優化了“100Hz占比”、“THD”特征值的計算公式；其次構造了變壓器工況模糊評價算法，提出了兩段式診斷流程；然后提出了振動特征值的截斷正態分布擬合方法，并采用合成少數類過采樣技術（Synthetic Minority Over-sampling Technique, SMOTE）對故障數據進行擴充，進一步提高分類準確度；最后隨機抽取測試數據對算法進行檢測，證明算法的準確性和有效性。

1 變壓器振動檢測分類模型的建立

1.1 振動特征值的選擇與優化

振動特征值法是目前廣泛采用的變壓器故障分析方法，此方法從變壓器的振動機理出發，構造振動信號特征值，實時計算其變化情況，并與同一變壓器歷史數據或同型號變壓器的正常工況數據進行比對，即可判斷被測變壓器的工作狀態。單個特征值的診斷效果往往有限，一般采取多個特征值聯合診斷的方法，其中使用較多的包括100Hz占比和總諧波畸變率（THD）。變壓器內部發生繞組變形、機械部件松動等故障時，線匝的位移、預緊力的缺失使得鐵心、繞組的模態特性和受力情況趨于復雜，由文獻[4,10,16]的實測結果可知，上述故障時的振動特征常表現為頻譜基頻占比下降、高頻占比增大、頻譜復雜度增大。100Hz占比反映變壓器基頻振動比例，傳統計算公式為[4,8,15,17]

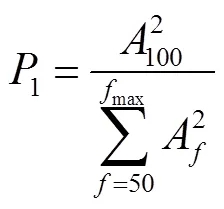
式中，A為頻譜中頻率點（單位為Hz）處的幅值，m/s2或V；100為頻譜中基頻幅值，即=100Hz時的幅值；max為考慮的最大頻率。

THD反映變壓器振動的諧波含量，文獻[10]中采用的計算式為

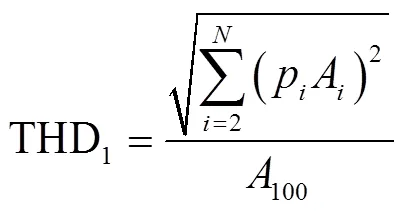
式中，A為第次諧波幅值；為諧波次數；p為第次諧波的權重，滿足p=。其理論依據為故障常導致振動高次諧波分量增加，其頻率與故障嚴重程度呈正相關，將高次諧波賦予更高權重可使得較小的高頻分量提升也能引起特征值的顯著增大，對故障更加靈敏。文獻[18]中采用的計算式為

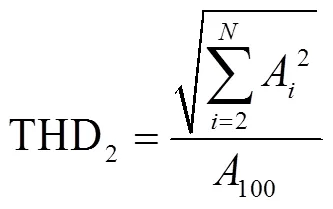
可以看出，式（1）將頻譜中100Hz作為變壓器正常運行的唯一特點，將50Hz等奇次諧波與200Hz等倍頻分量作為故障的特征；式（2）、式（3）以100Hz為基波，以倍頻分量為諧波，通過計算諧波比重實現故障診斷。但如前文所述，變壓器在正常運行時仍可能產生較大比例的倍頻振動分量。某330kV和500kV變壓器正常運行時于油箱壁測得的振動頻譜如圖1所示。由于受振動的非線性[19]和共振的影響，頻譜中倍頻幅值大于基頻幅值，此時使用100Hz占比進行故障診斷將產生較大的誤差。開展多變壓器橫向比較時，不同電壓等級的變壓器尺寸不同，使其共振特征頻率差異較大，導致頻譜諧波比重各異，使得THD閾值劃分困難，影響分類效果。

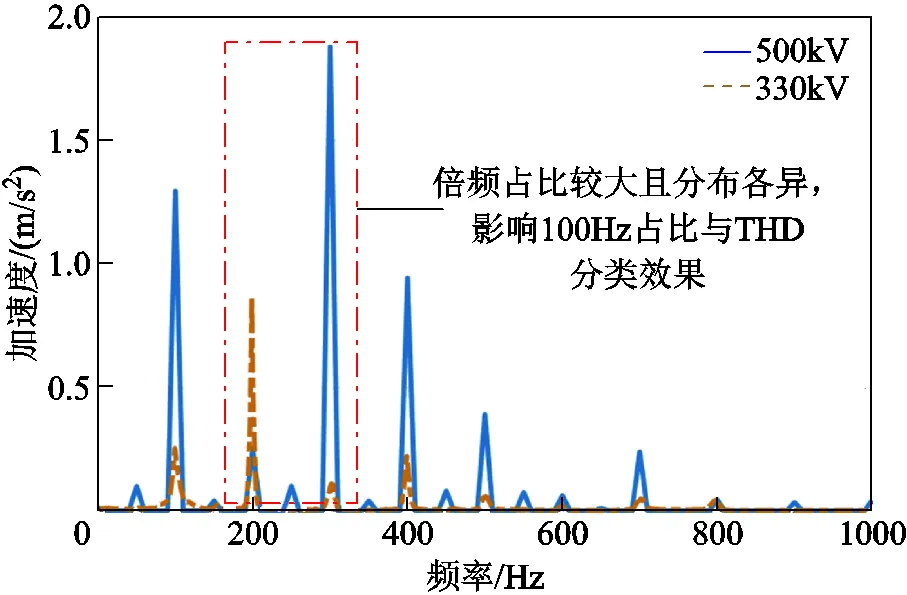
圖1 某330kV和500kV變壓器正常工況下的振動頻譜

為減小倍頻的影響，本文將低頻倍頻分量納入正常范圍，對兩特征值進行如下修改：①將100Hz占比改為低頻占比；②將THD的基頻由100Hz改為100Hz和較低頻率的倍頻，稱為倍頻THD。兩特征值相應的計算式分別為

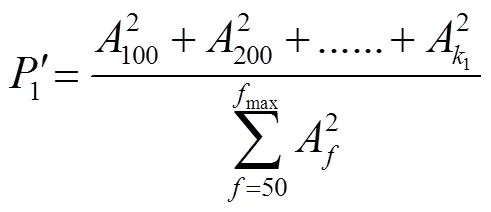
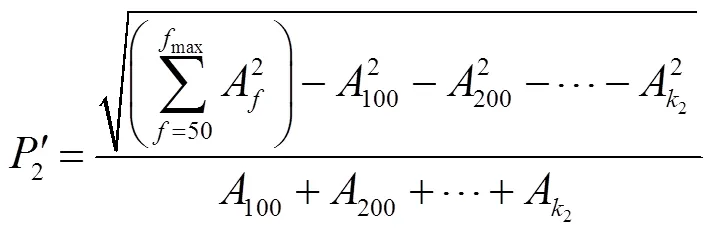
式中，1、2分別為兩特征值中正常工況的頻率上限。

除上述兩特征值外，另選取了奇偶次諧波比、振動熵、低頻奇偶比三個特征值。

1）奇偶次諧波比3，反映直流偏磁等故障造成的頻譜奇次諧波增大現象[15]。

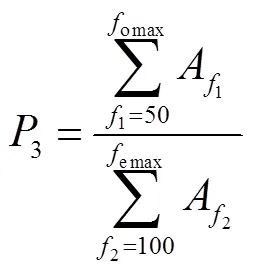
2）振動熵4，取自信息熵的概念，反映頻譜能量的離散程度。變壓器發生繞組變形或機械松動時頻譜能量集中度下降，導致振動熵增大[8]。

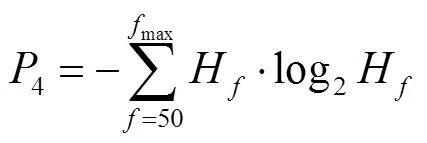
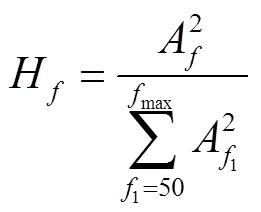
式中，H為頻率（單位為Hz）處的振動能量占比。

3）低頻奇偶比5。作為奇偶次諧波比的補充，奇偶次諧波比反映頻譜全局情況，變壓器故障較輕時不足以引起高頻率奇次分量的大幅增長。

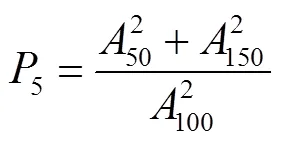
式（4）～式（9）中，式（6）的求和步長為100Hz，其余式中求和步長為50Hz。

本文以上述五個特征值為基礎，建立了用于多變壓器橫向對比的故障診斷模型。

1.2 基于截斷正態擬合的一次診斷過程

不同特征值對不同故障類型的敏感度不同，為避免各特征值間互相影響，將總診斷流程劃分為一次診斷和二次診斷兩部分，兩段式診斷流程示意圖如圖2所示。

一次診斷部分采用低頻占比、倍頻THD、振動熵三個特征值進行變壓器狀態的初步診斷，主要流程分為兩步：①使用包含正常與典型故障的不同電壓等級變壓器振動信號作為訓練集，分別計算其低頻占比、倍頻THD、振動熵并進行截斷正態擬合，得到正常、故障工況下三特征值的擬合曲線；②將正常、故障數據特征值的擬合曲線做比、歸一化可得到各特征值對應的診斷曲線，待測新數據通過與診斷曲線對應即可實現初步分類。以低頻占比為例的一次診斷流程如圖3所示，故障常導致變壓器低頻振動占比下降，因此其數據分布與擬合曲線均表現為正常樣本較高，故障樣本較低的特點。

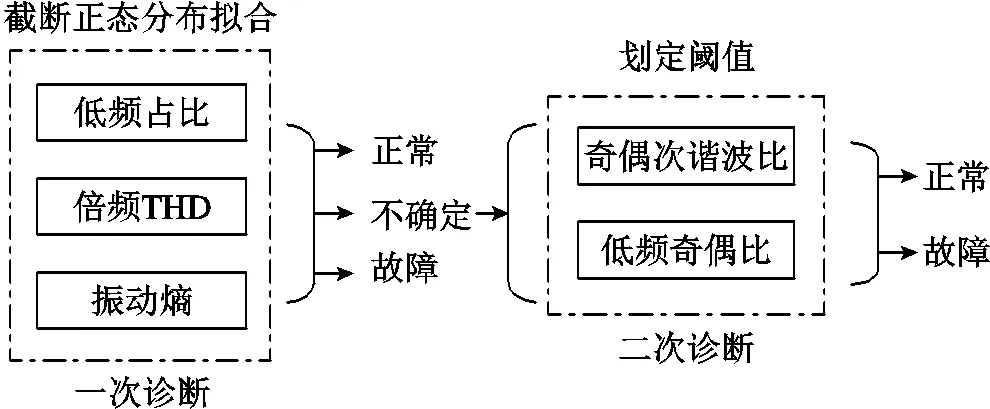
圖2 兩段式診斷流程示意圖

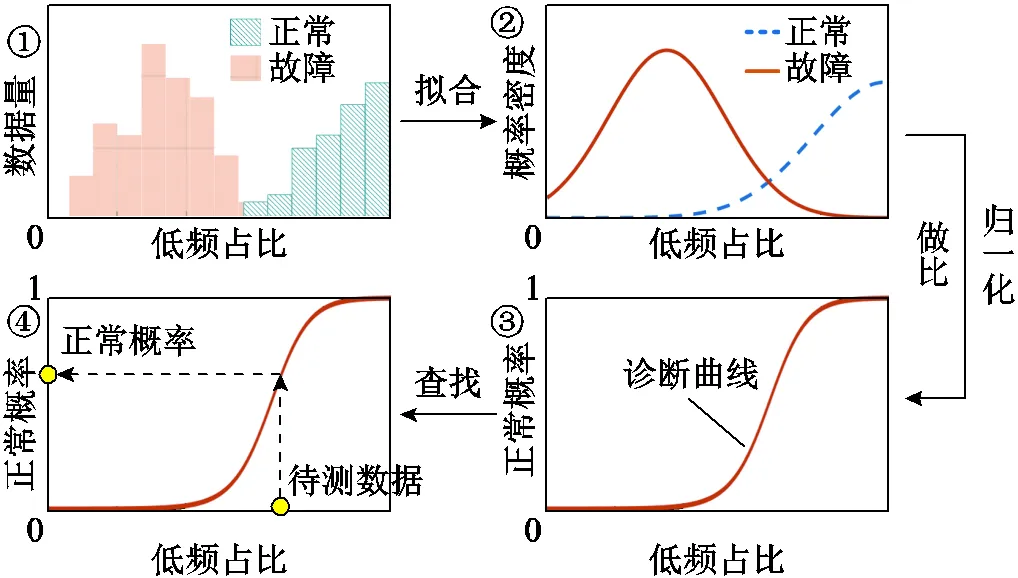
圖3 一次診斷流程

由于各特征值均有定義域限制，因此本文摒棄傳統的正態擬合，改用截斷正態擬合，其概率密度函數為

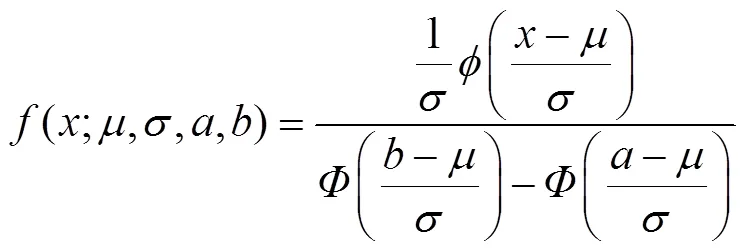
式中，和分別為未截斷之前數據的平均值和標準差；(·)為標準正態分布概率密度函數；(·)為標準正態分布的累積分布函數；和分別為截斷的下、上閾值。由參考文獻[20]可知，針對平均值為、標準差為、截斷下界為l、截斷上界為r的截斷正態分布(,2;l,r)，有

其中

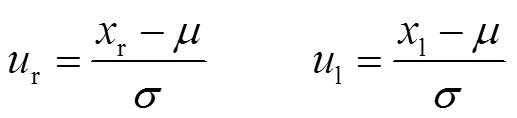
式中，為截斷正態分布的概率密度函數；為要進行截斷正態分布擬合的數據數量。使用牛頓-拉夫遜法迭代求解式（11）中的偏微分方程組即可得到,的估計值。

變壓器正常、故障的界限具有模糊性，因此定義同一特征值下正常、故障數據的截斷正態概率密度曲線之比為該特征值的“診斷曲線”，以此反映某數據來自正常運行變壓器的概率（如圖3中的③所示）。

使用變異系數法確定三個特征值的權重，流程如下：

1）計算訓練集各特征值的均值μ和標準差σ。

2）計算變異系數v，v=σ/μ。

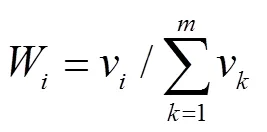
設某測試數據的三個特征值對應到各自診斷函數的結果分別為1、2、3，則聯合診斷結果為

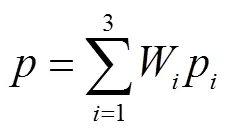
式中，p為某未知數據來自健康變壓器的概率。通過對p劃定閾值S1、S2可對待測變壓器工況進行進一步分類，一次診斷變壓器工況分類原則如圖4所示。

綜上所述，一次診斷的總流程如下：

1）對待測數據頻譜進行低頻占比、倍頻THD、振動熵特征值計算。

2）將各特征值計算結果分別對照各自的診斷曲線，讀取正常概率值。

3）由式（12）計算得到聯合診斷結果。

4）若≥2，直接判定為正常；若≤1，直接判定為故障；若1＜＜2，將數據標記為“不確定”，發送至二次診斷進一步分類。

1.3 二次診斷過程

二次診斷使用奇偶次諧波比、低頻奇偶比兩個特征值進行不確定數據的進一步分類，采取劃定閾值的方法，將特征值處于正常閾值之外的樣本直接判定為故障，其流程如圖5所示。

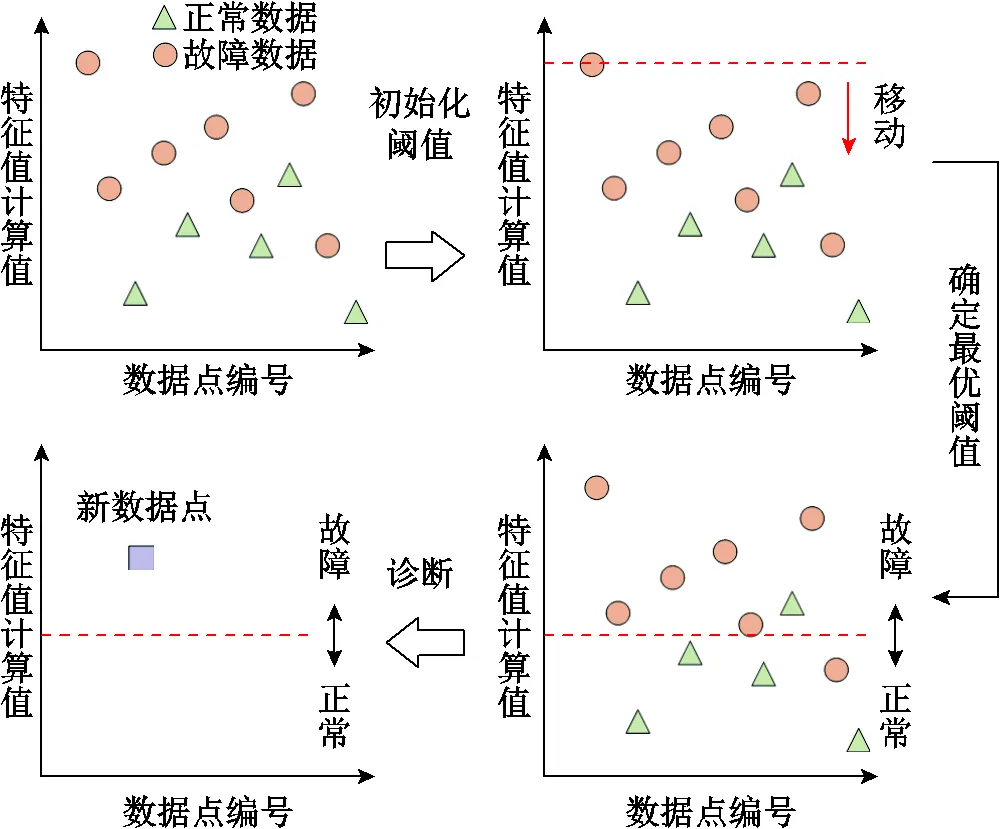
圖5 二次診斷流程

兩特征值閾值確定流程與工況判定準則如下：

1）使用訓練集數據對二次診斷模型進行訓練，計算其奇偶次諧波比、低頻奇偶比。

2）以計算結果最大值作為初始閾值。

3）向下移動閾值，實時記錄特征值診斷正確度，確定正確度最高的最優閾值。

4）若某不確定數據的任一特征值計算結果大于對應閾值，即判定為故障。

兩特征值的二次診斷閾值經訓練集確定后，對于新輸入的測試集可以直接對照此閾值進行診斷。

2 正常工況振動頻率區間的確定

為了確定變壓器正常工況下的振動頻率分布區間，進而確定式（4）、式（5）中1、2的最優取值，搜集整理了文獻[4, 6, 21-41]中的數據和現場測得的數據共104組，包括69組正常工況數據和35組故障工況數據，對應變壓器電壓等級范圍為2～500kV，涉及工作狀態包含空載、輕載和額定負載，數據詳細信息見表1。隨機選擇54組正常數據與23組故障數據作為訓練集，15組正常數據與12組故障數據作為測試集，統計訓練集除100Hz基頻外的振動主頻分布結果如圖6所示。由圖6可見，不考慮基頻時，正常變壓器的振動主頻主要分布在200Hz和300Hz，分布于400Hz和500Hz的數據量較少，而故障變壓器的振動主頻在150～600Hz范圍內分布較為均勻。

表1 變壓器振動數據信息

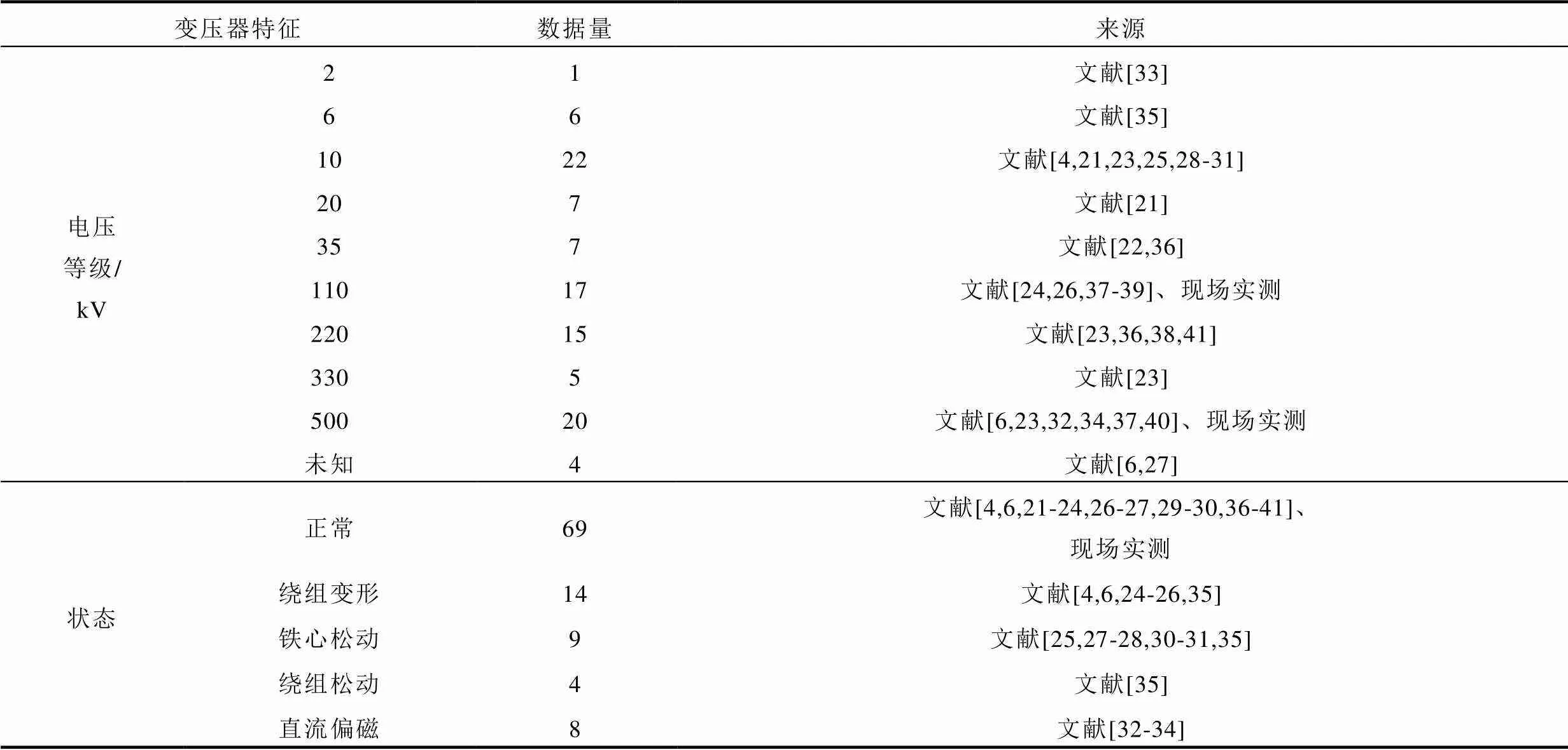
Tab.1 Vibration data information

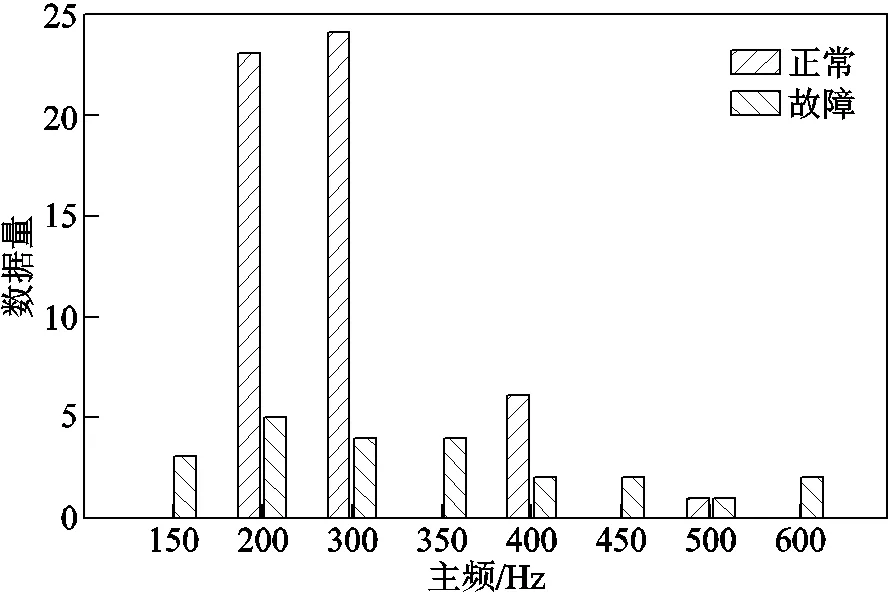
圖6 訓練集數據振動主頻統計直方圖

基于以上分析，取1、2為200～500Hz，max為1kHz，以區間重合度表征低頻占比、倍頻THD對訓練集數據的分類效果。區間重合度的定義為：給定兩個集合、，其區間重合度為、交集大小與、并集大小的比值，即

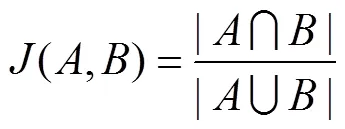
區間重合度越大表明兩集合的重疊區域越多，特征值分類效果越差，其上限為1。不同1、2取值下兩優化特征值分類效果見表2。

表2 不同1、2取值下兩優化特征值分類效果

Tab.2 Classification effect of two optimized eigenvalues under different k1 and k2 values

從表2可知，當1、2均取400Hz時兩特征值具有最優的分類效果，因此將100Hz、200Hz、300Hz和400Hz作為正常的指標，將500Hz等高次倍頻分量與奇次諧波作為故障的指標。為了對比兩優化特征值和原特征值的分類效果，分別計算了77組訓練集數據的100Hz占比、低頻占比、THD、倍頻THD，結果分別如圖7、圖8所示。

由圖7和圖8可見，兩優化特征值相比于原特征值分類效果明顯提升，抗振動倍頻干擾能力增強，其分類結果的區間重合度顯著下降，分類效果分別提升了79%、76%。圖8中三特征值的縱坐標相差較大，是由于THD1對應的式（2）與THD2對應的式（3）將100Hz作為基頻置于分母，使得計算值由于分子倍頻分量的影響被抬高，并且式（2）中將高次諧波賦予更高權重，導致計算結果進一步增大。而倍頻THD對應的式（5）將100～400Hz置于分母，緩解了倍頻分量對結果的抬高作用。

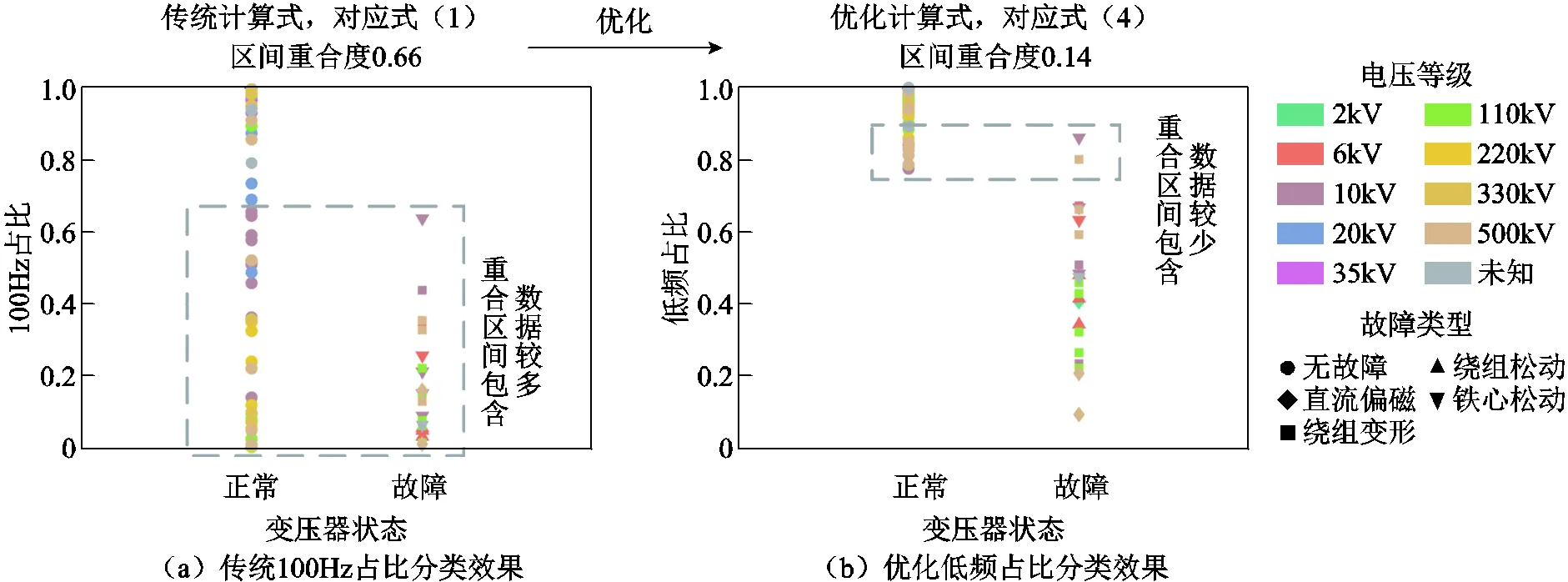
圖7 100Hz占比優化效果

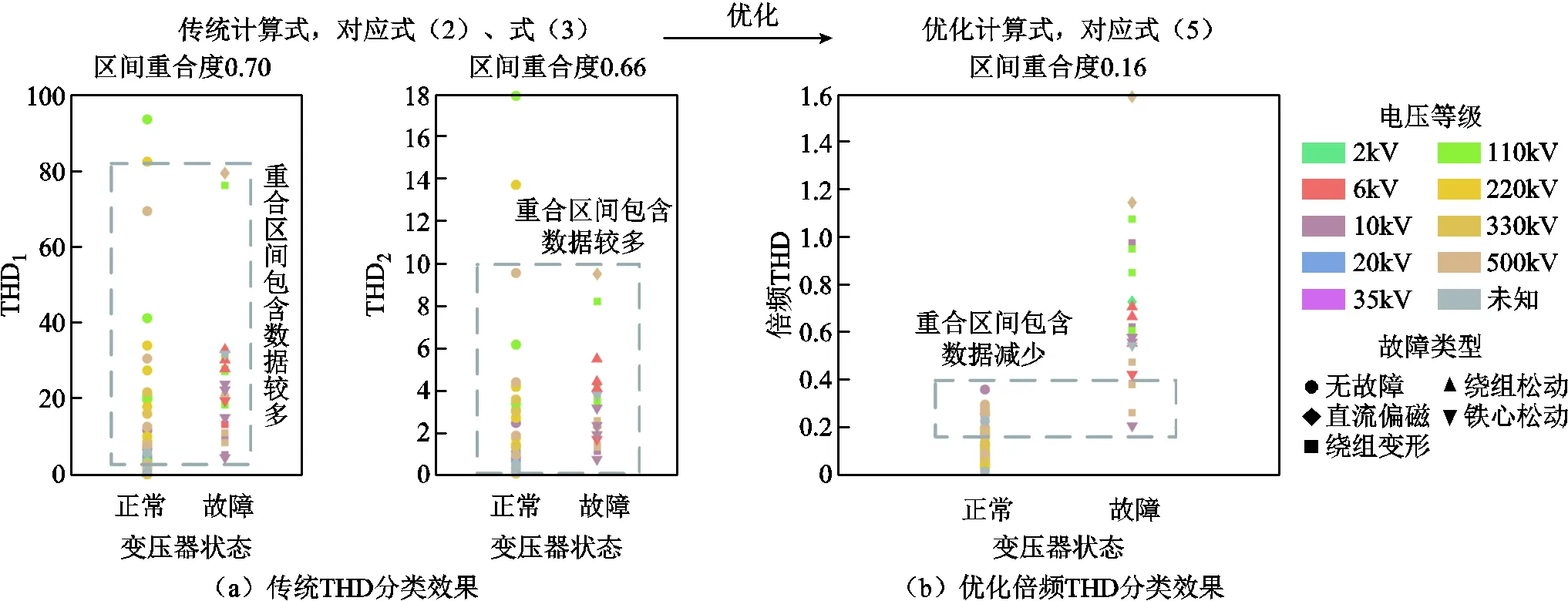
圖8 THD優化效果

3 故障檢測模型的測試

3.1 模型訓練過程

為檢驗模型整體的分類效果，使用77組訓練集訓練模型的截斷正態擬合曲線、診斷曲線與分類閾值，使用27組測試集對模型進行檢測。

首先按式（10）、式（11）對各特征值進行截斷正態擬合訓練，正常數據倍頻THD特征值的分布直方圖和擬合曲線如圖9所示。可見，擬合曲線能較好地反映特征值的分布情況，表明使用截斷正態分布擬合具有合理性。訓練集低頻占比的概率密度曲線和診斷曲線如圖10所示。

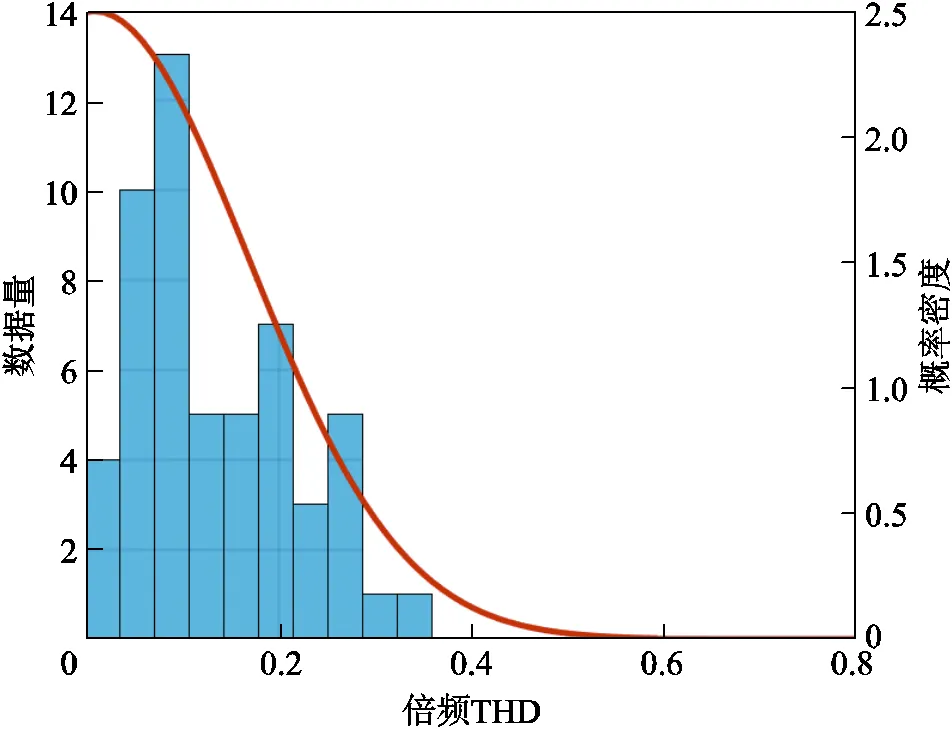
圖9 訓練集正常工況數據倍頻THD特征值的分布直方圖和擬合曲線

使用1.2節介紹的變異系數法計算一次診斷中三特征值的權重，結果見表3。

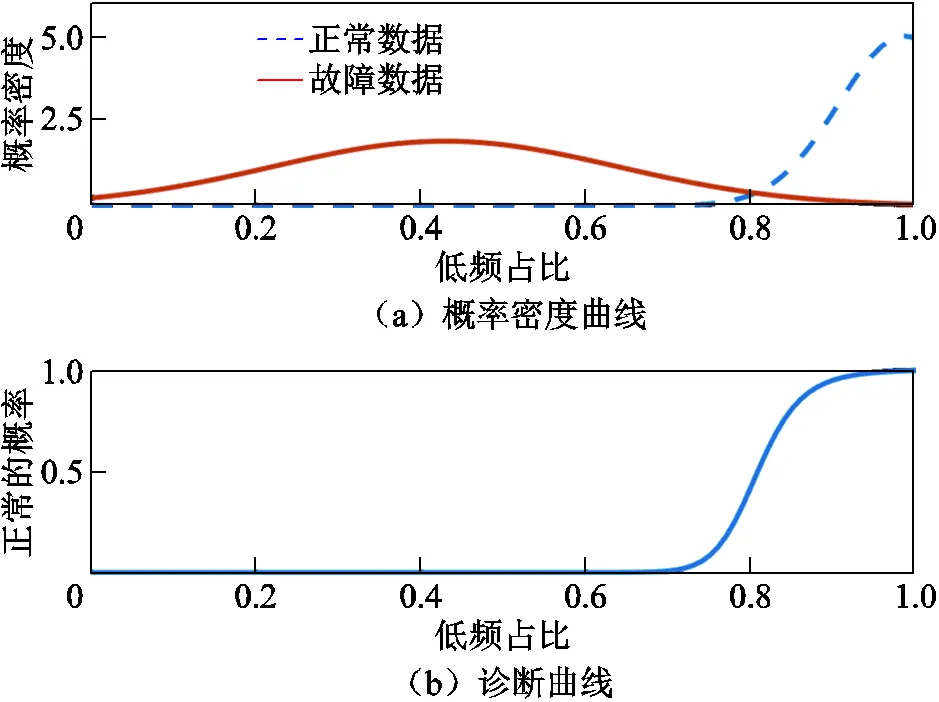
圖10 訓練集低頻占比概率密度曲線與診斷曲線

表3 一次診斷特征值權重

Tab.3 Primary diagnostic eigenvalue weight

本文雖收集了大量數據，但由于實際情況中故障的變壓器較少，因此仍存在故障數據不足的問題。為緩解數據不平衡對分類效果的影響，使用SMOTE算法對故障數據進行擴充，使得故障數據量由23組擴充為54組，與正常數據量相等。

由于SMOTE算法應用十分廣泛，已有不少學者對此進行了深入研究，本文不再贅述，SMOTE算法原理和在變壓器故障診斷領域的應用可參閱文獻[42]。

將擴充后的共108組訓練集數據輸入一次診斷，其結果如圖11所示，計算正常、故障數據診斷結果的平均值分別為0.860、0.087，將其作為“正常閾值”與“故障閾值”，分別對應圖4中的2、1。

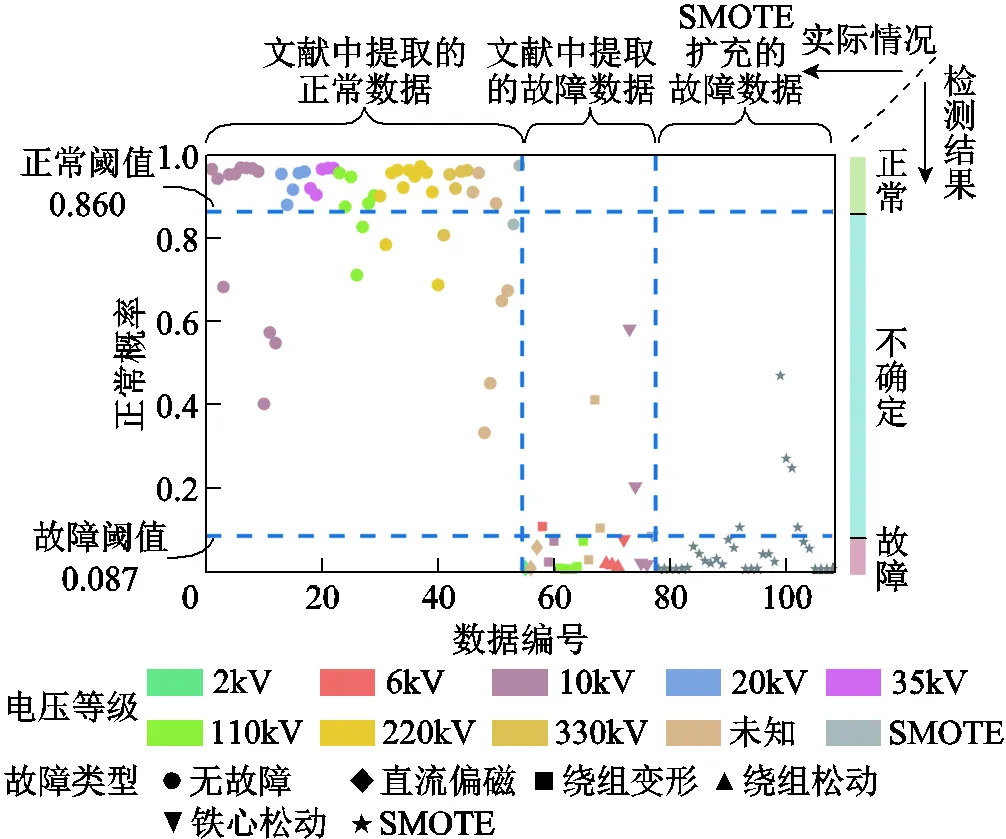
圖11 算法對擴充后訓練集數據的一次診斷結果

由圖11可知，一次診斷成功地將故障數據與正常數據進行了初步區分，大部分正常樣本的正常概率計算結果高于閾值，判定結果符合實際情況。但由于變壓器工況模糊性因素的存在，部分正常樣本被診斷為了“不確定”。故障樣本中直流偏磁、繞組松動和大部分SMOTE擴充樣本成功診斷為故障，部分繞組變形、鐵心松動樣本被診斷為“不確定”。

將圖11中除SMOTE擴充數據外的20組“不確定”數據發送至1.3節所述的二次診斷部分，特征值閾值計算結果見表4，診斷結果如圖12所示。圖12中虛線對應數據表示兩特征值閾值，二次診斷在全部20組不確定數據中正確診斷出13組，起到了對一次診斷的補充作用。

表4 二次診斷特征值閾值

Tab.4 Eigenvalue threshold in secondary diagnosis

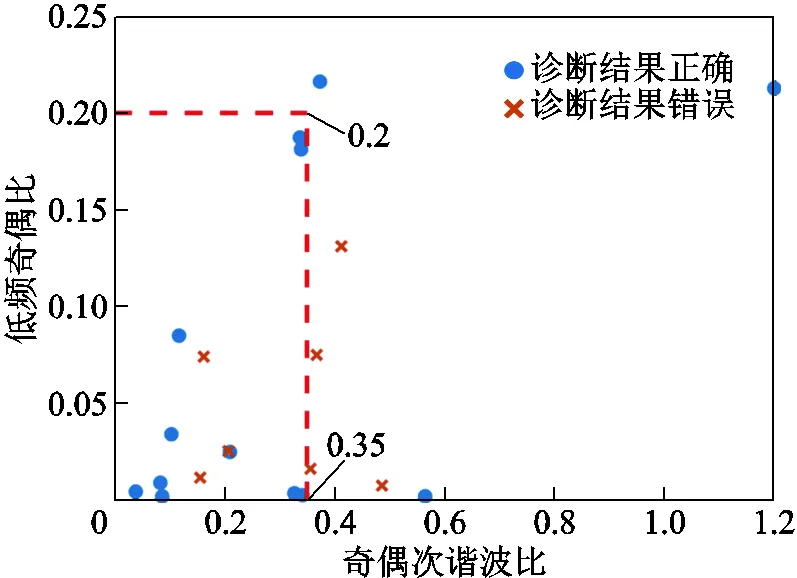
圖12 算法對20組訓練集不確定數據的二次診斷結果

上述針對訓練集數據的一次診斷和二次診斷正確分類出70組樣本，準確度達到91%，表明訓練得到的截斷正態擬合曲線、診斷函數以及判定閾值對多變壓器的橫向診斷具有一定的合理性與適用性。

3.2 模型測試過程

上述27組測試集數據中包含15組正常樣本、3組鐵心松動樣本、3組繞組變形樣本、1組繞組松動樣本和5組直流偏磁樣本。將測試集數據輸入經過訓練的模型，其一次診斷與二次診斷結果分別如圖13、圖14所示。可以看出，一次診斷后，有11組數據被判定為“不確定”；二次診斷后，所有的故障數據均被正確診斷出，但有兩組正常數據被誤診為故障，算法對于不同電壓等級的變壓器分類準確度達到92.6%。

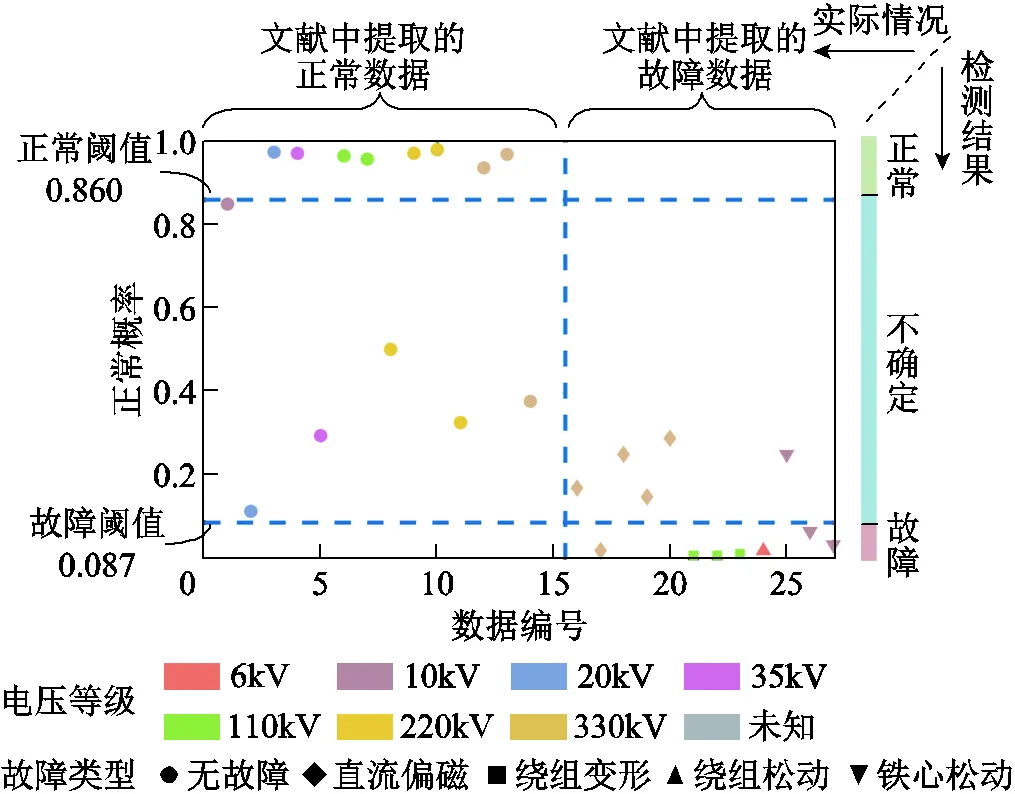
圖13 訓練完成的算法對測試集數據的一次診斷結果

圖14 訓練完成的算法對11組不確定數據的二次診斷結果

圖14中部分數據的低頻奇偶比較大，主要原因是①～③號數據的故障類型均為直流偏磁，故障時變壓器在直流磁場的影響下出現鐵心磁場半波飽和，表現為低頻奇次諧波振動分量顯著增大，進而引起低頻奇偶比升高。

為了評估測點位置對模型的影響，對一臺500kV變壓器正常運行時多測點的振動開展了實測，振動測點布置位置如圖15所示。以圖15中各測點測量結果為正常數據集，以文獻[24]中對110kV變壓器繞組變形時六個測點的測量結果為故障數據集，算法一次診斷結果如圖16所示。其中，故障測點的布置位置與圖15相似，均位于油箱壁表面對應三相繞組處。結果表明一次診斷實現了多測點數據的正確分類，算法適用于來自不同測點數據的診斷。

圖15 振動測點布置位置

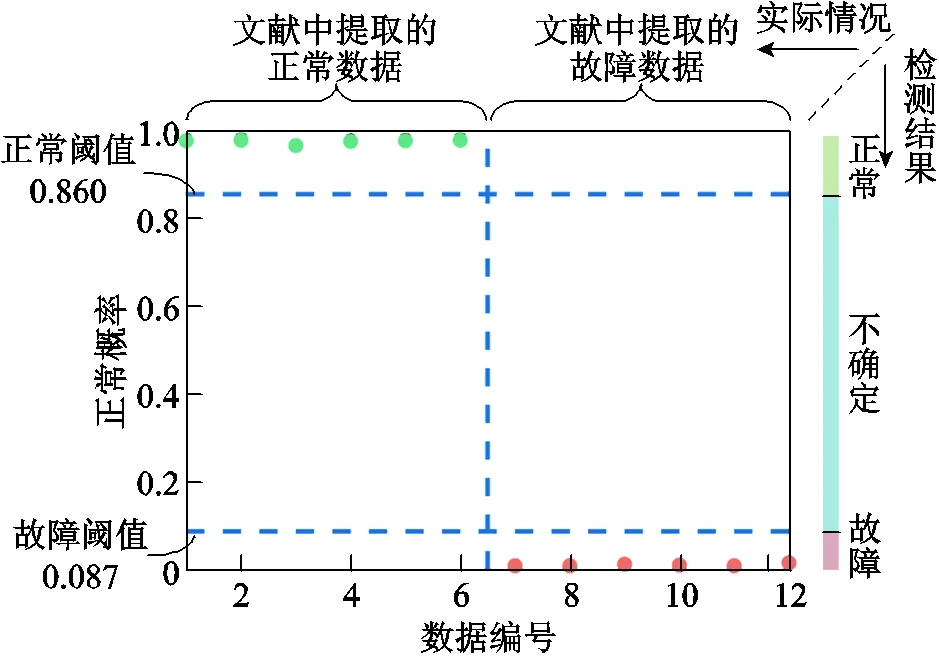
圖16 算法對500kV變壓器正常、110kV變壓器繞組變形下各六個測點的一次診斷結果

為了評估模型是否適用于不同工作狀態下的振動樣本分類，使用15組測試集進行測試，數據信息見表5。算法一次、二次診斷結果分別如圖17、圖18所示，整體診斷正確率較高，僅將一組故障樣本誤診為正常，表明算法適用于不同工作狀態下數據的診斷。

表5 包含不同工作狀態的15組測試集數據信息

Tab.5 Contains 15 sets of test set data information with different working states

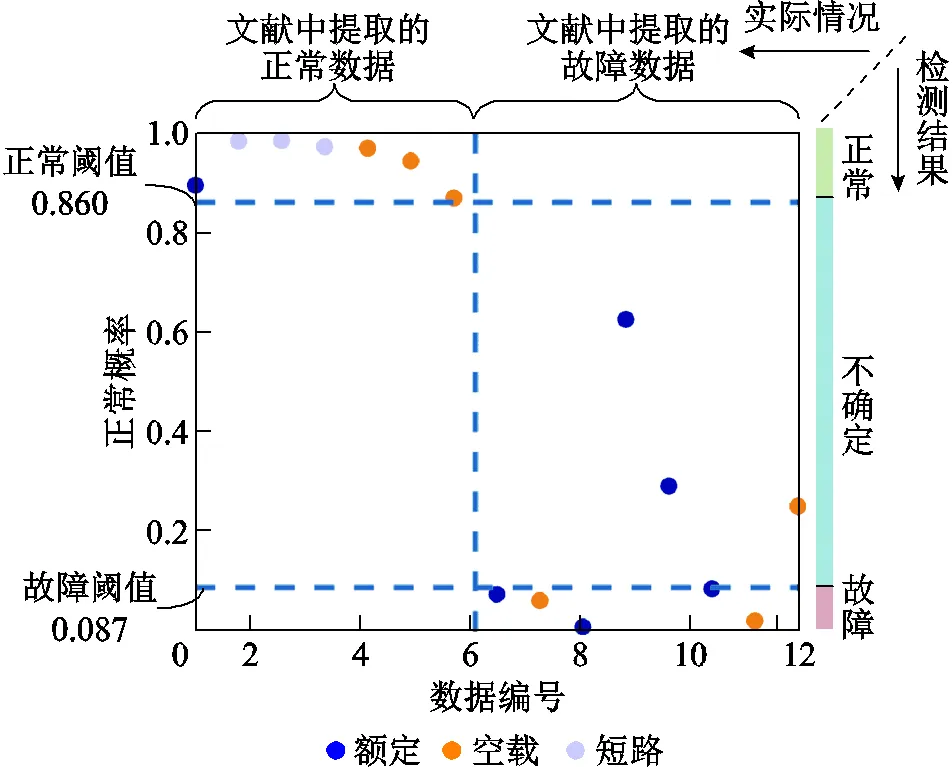
圖17 對15組包含不同工作狀態數據的一次診斷結果

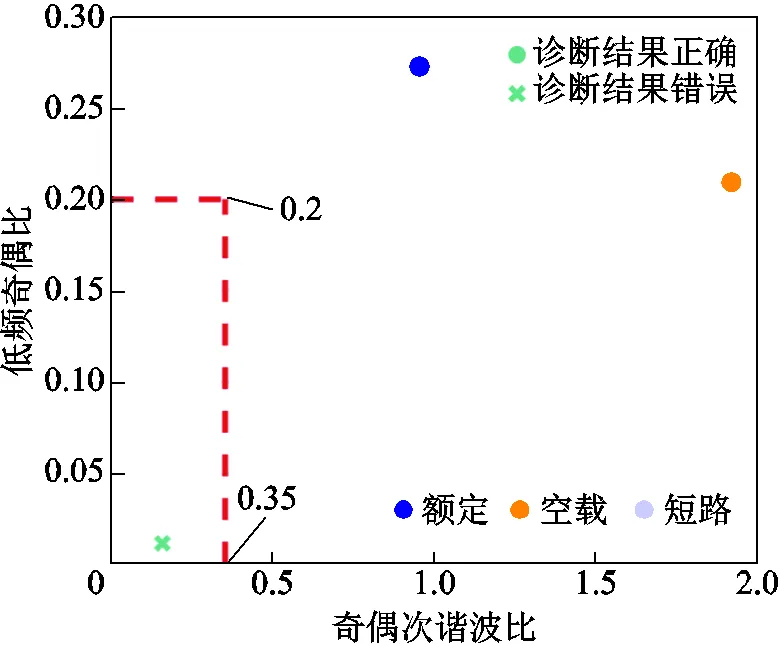
圖18 對15組包含不同工作狀態數據的二次診斷結果

4 結論

本文搜集整理了各電壓等級變壓器正常和典型故障下的振動信號，提出了一種基于振動特征值的多變壓器故障橫向診斷方法。主要結論如下：

1）統計了變壓器振動主頻分布情況，將100～400Hz分量納入正常的范圍，對傳統的100Hz占比、總諧波畸變率計算式進行了改進，大幅提升了兩特征值的分類效果。

2）構造了兩段式診斷流程，一次診斷使用截斷正態函數進行數據擬合，考慮了特征值定義域限制與變壓器工況界限的模糊性；二次診斷對一次診斷的“不確定”數據進行進一步分類。

3）使用SMOTE算法對故障數據進行擴充，緩解了數據不足和類別不平衡的問題。

4）使用27組數據進行測試，結果表明算法對正常、故障變壓器的分類準確度達到92.6%，適用于不同變壓器的橫向診斷和對不同測點、不同工作狀態數據的分類。

[1] 汲勝昌, 程錦, 李彥明. 油浸式電力變壓器繞組與鐵心振動特性研究[J]. 西安交通大學學報, 2005, 39(6): 616-619, 658.

Ji Shengchang, Cheng Jin, Li Yanming. Research on vibration characteristics of windings and core of oil-filled transformer[J]. Journal of Xi'an Jiaotong University, 2005, 39(6): 616-619, 658.

[2] Lavalle J C. Failure detection in transformers using vibrational analysis[D]. Cambridge: Massachusetts Institute of Technology, 1986.

[3] 程錦, 李延沐, 汲勝昌, 等. 振動法在線監測變壓器繞組及鐵心狀況[J]. 高電壓技術, 2005, 31(4): 43-45, 48.

Cheng Jin, Li Yanmu, Ji Shengchang, et al. Application of vibration method on monitoring the winding and core condition of transformer[J]. High Voltage Engineering, 2005, 31(4): 43-45, 48.

[4] 馬宏忠, 耿志慧, 陳楷, 等. 基于振動的電力變壓器繞組變形故障診斷新方法[J]. 電力系統自動化, 2013, 37(8): 89-95.

Ma Hongzhong, Geng Zhihui, Chen Kai, et al. A new fault diagnosis method for power transformer winding deformation based on vibration[J]. Automation of Electric Power Systems, 2013, 37(8): 89-95.

[5] 熊衛華, 趙光宙. 基于希爾伯特-黃變換的變壓器鐵心振動特性分析[J]. 電工技術學報, 2006, 21(8): 9-13.

Xiong Weihua, Zhao Guangzhou. Analysis of transformer core vibration characteristics using Hilbert-Huang transformation[J]. Transactions of China Electrotechnical Society, 2006, 21(8): 9-13.

[6] 郭俊, 汲勝昌, 沈琪, 等. 盲源分離技術在振動法檢測變壓器故障中的應用[J]. 電工技術學報, 2012, 27(10): 68-78.

Guo Jun, Ji Shengchang, Shen Qi, et al. Blind source separation technology for the detection of transformer fault based on vibration method[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 68-78.

[7] 汲勝昌, 劉味果, 單平, 等. 小波包分析在振動法監測變壓器鐵芯及繞組狀況中的應用[J]. 中國電機工程學報, 2001, 21(12): 24-27.

Ji Shengchang, Liu Weiguo, Shan Ping, et al. The application of the wavelet packet to the monitoring of the core and winding condition of transformer[J]. Proceedings of the CSEE, 2001, 21(12): 24-27.

[8] 劉云鵬, 王博聞, 周旭東, 等. 基于162臺超、特高壓變壓器的聲紋特征預警閾值劃定研究[J]. 華北電力大學學報(自然科學版), 2021, 48(5): 45-53.

Liu Yunpeng, Wang Bowen, Zhou Xudong, et al. Threshold delineation research for early warning of voiceprint eigenvalues based on 162 sets of EHV and UHV transformers[J]. Journal of North China Electric Power University (Natural Science Edition), 2021, 48(5): 45-53.

[9] Bagheri M, Zollanvari A, Nezhivenko S. Transformer fault condition prognosis using vibration signals over cloud environment[J]. IEEE Access, 2018, 6: 9862-9874.

[10] Bartoletti C, Desiderio M, Di Carlo D, et al. Vibro-acoustic techniques to diagnose power transformers[J]. IEEE Transactions on Power Delivery, 2004, 19(1): 221-229.

[11] 趙莉華, 徐立, 劉艷, 等. 基于點對稱變換與圖像匹配的變壓器機械故障診斷方法[J]. 電工技術學報, 2021, 36(17): 3614-3626.

Zhao Lihua, Xu Li, Liu Yan, et al. Transformer mechanical fault diagnosis method based on symmetrized dot patter and image matching[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3614-3626.

[12] 李夢星, 張艷麗, 姜偉, 等. 機械應力下電工鋼片磁滯與磁致伸縮回環滯后特性模擬[J]. 電工技術學報, 2022, 37(11): 2698-2706.

Li Mengxing, Zhang Yanli, Jiang Wei, et al. Simulation of hysteresis and magnetostrictive loop hysteretic characteristics of electrical steel sheets under mechanical stress[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2698-2706.

[13] 李勁松, 梁振宗, 孫英倫, 等. 閉合Fe-Si結構中磁致伸縮引起的機械共振研究[J]. 電工技術學報, 2022, 37(6): 1321-1328.

Li Jinsong, Liang Zhenzong, Sun Yinglun, et al. Study of mechanical resonance induced by magnetostriction in closed structures based on Fe-Si[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1321-1328.

[14] 遲青光, 張艷麗, 陳吉超, 等. 非晶合金鐵心損耗與磁致伸縮特性測量與模擬[J]. 電工技術學報, 2021, 36(18): 3876-3883.

Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of loss and magnetostrictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.

[15] 余長廳, 黎大健, 陳梁遠, 等. 基于聲紋及振動的變壓器故障診斷技術研究[J]. 高壓電器, 2019, 55(11): 248-254.

Yu Zhangting, Li Dajian, Chen Liangyuan, et al. Transformer fault diagnosis technique based on voiceprint and vibration[J]. High Voltage Apparatus, 2019, 55(11): 248-254.

[16] Hong Kaixing, Huang Hai, Fu Yaqiong, et al. A vibration measurement system for health monitoring of power transformers[J]. Measurement, 2016, 93: 135-147.

[17] 潘志城, 鄧軍, 謝志成, 等. 換流變壓器和交流變壓器振動信號特征的比較分析[J]. 變壓器, 2020, 57(3): 35-40.

Pan Zhicheng, Deng Jun, Xie Zhicheng, et al. Comparion and analysis of characteristics of vibration signal of converter transformer and AC transformer[J]. Transformer, 2020, 57(3): 35-40.

[18] Bagheri M, Nezhivenko S, Naderi M S, et al. A new vibration analysis approach for transformer fault prognosis over cloud environment[J]. International Journal of Electrical Power & Energy Systems, 2018, 100: 104-116.

[19] 鐘思翀, 祝麗花, 王前超, 等. 電力變壓器振動噪聲分析及其有源降噪[J]. 電工技術學報, 2022, 37(增刊1): 11-21.

Zhong Sichong, Zhu Lihua, Wang Qianchao, et al. Electromagnetic vibration of power transformer and active noise reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 11-21.

[20] 章棟恩. 截斷正態分布參數估計的EM算法[J]. 北京輕工業學院學報, 1998, 16(2): 72-76.

Zhang Dong'en. Estimation of parameter for truncated normal distribution via the EM algorithm[J]. Journal of Beijing Institute of Light Indusry, 1998, 16(2): 72-76.

[21] 鄭婧, 王婧頔, 郭潔, 等. 電力變壓器鐵心振動特性分析[J]. 電子測量與儀器學報, 2010, 24(8): 763-768.

Zheng Jing, Wang Jingdi, Guo Jie, et al. Vibration analysis of power transformer cores[J]. Journal of Electronic Measurement and Instrument, 2010, 24(8): 763-768.

[22] 洪凱星, 潘再平, 黃海. 電力變壓器繞組軸向振動的建模與分析[J]. 變壓器, 2010, 47(12): 32-36.

Hong Kaixing, Pan Zaiping, Huang Hai. Modeling and analysis of winding axial vibration of power transformer[J]. Transformer, 2010, 47(12): 32-36.

[23] 朱葉葉, 汲勝昌, 張凡, 等. 電力變壓器振動產生機理及影響因素研究[J]. 西安交通大學學報, 2015, 49(6): 115-125.

Zhu Yeye, Ji Shengchang, Zhang Fan, et al. Vibration mechanism and influence factors in power transformers[J]. Journal of Xi'an Jiaotong University, 2015, 49(6): 115-125.

[24] Hong Kaixing, Huang Hai, Zhou Jianping. Winding condition assessment of power transformers based on vibration correlation[J]. IEEE Transactions on Power Delivery, 2015, 30(4): 1735-1742.

[25] 劉勝軍, 孫志鵬, 沈辰, 等. 基于振動頻譜分析和總諧波畸變率的電力變壓器故障診斷方法研究[J]. 電網與清潔能源, 2021, 37(3): 86-91.

Liu Shengjun, Sun Zhipeng, Shen Chen, et al. Research on fault diagnosis of power transformers based on spectral analysis of vibration signals and total harmonic distortion[J]. Power System and Clean Energy, 2021, 37(3): 86-91.

[26] Hong Kaixing, Jin Ming, Huang Hai. Transformer winding fault diagnosis using vibration image and deep learning[J]. IEEE Transactions on Power Delivery, 2021, 36(2): 676-685.

[27] 吳書有. 基于振動信號分析方法的電力變壓器狀態監測與故障診斷研究[D]. 合肥: 中國科學技術大學, 2009.

[28] 郝震, 龍凱華, 趙燕坤, 等. 引起變壓器異常振動的兩種缺陷的診斷[J]. 中國電力, 2014, 47(6): 55-60, 65.

Hao Zhen, Long Kaihua, Zhao Yankun, et al. Abnormal vibration diagnostic methods of transformers caused by two defects[J]. Electric Power, 2014, 47(6): 55-60, 65.

[29] 高沛, 王豐華, 蘇磊, 等. 直流偏磁下電力變壓器的振動特性[J]. 電網技術, 2014, 38(6): 1536-1541.

Gao Pei, Wang Fenghua, Su Lei, et al. Analysis on vibration characteristics of power transformer under DC bias[J]. Power System Technology, 2014, 38(6): 1536-1541.

[30] Tian Haoyang, Peng Wei, Hu Min, et al. Feature extraction of the transformer core loosening based on variational mode decomposition[C]//2017 1st International Conference on Electrical Materials and Power Equipment (ICEMPE), Xi'an, China, 2017: 598-602.

[31] 王豐華, 王邵菁, 陳頌, 等. 基于改進MFCC和VQ的變壓器聲紋識別模型[J]. 中國電機工程學報, 2017, 37(5): 1535-1543.

Wang Fenghua, Wang Shaojing, Chen Song, et al. Voiceprint recognition model of power transformers based on improved MFCC and VQ[J]. Proceedings of the CSEE, 2017, 37(5): 1535-1543.

[32] 李冰, 王澤忠, 劉海波, 等. 直流偏磁下500kV單相變壓器振動噪聲的試驗研究[J]. 電工技術學報, 2021, 36(13): 2801-2811.

Li Bing, Wang Zezhong, Liu Haibo, et al. Experiment on vibro-acoustic characteristic of 500kV single-phase transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2801-2811.

[33] 王佳音, 白保東, 劉宏亮, 等. 直流偏磁對變壓器振動噪聲的影響[J]. 電工技術學報, 2015, 30(8): 56-61.

Wang Jiayin, Bai Baodong, Liu Hongliang, et al. Research on vibration and noise of transformers under DC bias[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 56-61.

[34] 陳青恒, 馬宏彬, 何金良. 直流偏磁引起的500kV電力變壓器振動和噪聲的現場測量與分析[J]. 高壓電器, 2009, 45(3): 93-96.

Chen Qingheng, Ma Hongbin, He Jinliang. Field monitoring and analysis on vibration and noise of 500 kV electrical transformer under DC current biasing[J]. High Voltage Apparatus, 2009, 45(3): 93-96.

[35] 羅世豪. 基于聲紋的干式變壓器典型缺陷識別研究[D]. 北京: 華北電力大學(北京), 2021.

[36] 陳彥文. 220kV油浸電力變壓器繞組變形在線診斷方法研究[D]. 沈陽: 沈陽工業大學, 2017.

[37] 朱柯佳. 高噪聲環境下變壓器聲紋特征提取方法研究[D]. 北京: 華北電力大學(北京), 2021.

[38] 吳國鑫. 變壓器故障聲紋檢測與診斷方法研究[D]. 北京: 華北電力大學(北京), 2021.

[39] Ding Qiaolin, Yuan Yimin, Li Zhong. A wavelet analysis of three-dimensional surface vibration signal of running power transformer[J]. Advanced Materials Research, 2014, 1049/1050: 634-637.

[40] Zheng Jing, Huang Hai, Hong Kaixing, et al. Blind source separation of vibration signals for fault diagnosis of power transformers[C]//2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 2014: 412-417.

[41] Ding Dengwei, Zhang Xinghai, Liu Rui, et al. Research on the winding and iron core operation state of transformer based on the vibration acoustic fingerprint[C]//2016 International Conference on Condition Monitoring and Diagnosis (CMD), Xi'an, China, 2016: 420-423.

[42] 劉云鵬, 和家慧, 許自強, 等. 基于SVM SMOTE的電力變壓器故障樣本均衡化方法[J]. 高電壓技術, 2020, 46(7): 2522-2529.

Liu Yunpeng, He Jiahui, Xu Ziqiang, et al. Equalization method of power transformer fault sample based on SVM SMOTE[J]. High Voltage Engineering, 2020, 46(7): 2522-2529.

Power Transformer Fault Detection Based on Multi-Eigenvalues of Vibration Signal

Du Houxian1Liu Hao1Lei Longwu2Tong Jie3Huang Jianye2Ma Guoming1

（1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Beijing 102206 China 2. State Grid Fujian Electric Power Research Institute Fuzhou 350007 China 3. China Electric Power Research Institute Beijing 100192 China）

Vibration signal analysis is an essential part of power transformer fault detection. The current researches mainly compare the transformers of a specific type or a single voltage level. The resulting detection algorithm is unsuitable for the transformers of different types, and the generality is poor. This paper proposed a power transformer fault detection algorithm based on vibration multi-eigenvalues to solve the above problem. The vibration signals of transformers under normal, winding deformation, winding loosening, core loosening, and DC magnetic bias statuses were collected, involving a voltage level range of 2～500kV. The above data were classified by using traditional eigenvalues of the 100Hz amplitude proportion, the total harmonic distortion (THD) considering high-frequency proportion and THD without considering high-frequency proportion, to verify whether the traditional eigenvalues have the ability of classification. The interval coincidence degree was used to represent the classification effect. The traditional eigenvalues were interfered by the harmonics of the vibration, and the interval coincidence degree of the classification results were 66%, 70% and 66%, respectively. The results showed that the traditional eigenvalues cannot be used to diagnose the transformers of different types.

According to the analysis of the transformer vibration spectrum, the vibration of core and winding is nonlinear and has an influence on the resonance of mechanical parts. This results in a particular proportion of harmonics in the transformer vibration spectrum under normal operation, which affects the classification effect of eigenvalues seriously.

In order to optimize the eigenvalues, the vibration harmonics of lower frequency were brought into normal range. Firstly, the main vibration frequency distribution of transformers under normal and fault conditions was obtained in this paper, which were distributed within 200～500Hz in normal situations, and were evenly distributed within 150～600Hz in cases of fault. By analyzing various frequency combinations, the 200～400Hz harmonic components were considered as normal situations to maximize the classification effect of the two eigenvalues. The optimized classification interval coincidence degrees of the low-frequency proportion and the upper THD were reduced to 14% and 16%, respectively. The classification accuracy was improved by 79% and 76%, compared with the original eigenvalues.

Because different eigenvalues have different sensitivities to various faults, a two-step fault detection process including primary and secondary diagnosis was proposed to avoid the influence of multiple eigenvalues. The primary diagnosis was based on low frequency proportion, upper THD and vibration entropy, and the SMOTE algorithm was used to expand the fault data to realize the balance of the data set. After that, the truncated normal distribution was used for data fitting and constructing the diagnosis function. By calculating the probability that the sample came from a normal transformer, the result was divided into three categories: normal, uncertain and fault. Based on the odd and even harmonics ratio and the low-frequency odd and even harmonics ratio, the data diagnosed as "uncertain" in the primary diagnosis were further classified by demarcating threshold in the secondary diagnosis. The testing set was used to test the overall algorithm classification effect, and the results showed that the fault diagnosis accuracy was up to 92.6%.

In summary, the method proposed in this paper is suitable for transformer detection with different types, different measuring point distributions and different working conditions.

Power transformer, vibration, eigenvalue, transverse diagnosis, two-step diagnosis

10.19595/j.cnki.1000-6753.tces.221422

TM41

杜厚賢 男，2000年生，博士研究生，研究方向為電力設備狀態檢測與故障診斷。E-mail：Du_houxian@163.com

馬國明 男，1984年生，教授，博士生導師，研究方向為電氣設備在線監測與故障診斷，高電壓與絕緣技術。E-mail：ncepumgm@163.com（通信作者）

國家電網有限公司科技資助項目（5700-202121258A-0-0-00）。

2022-07-24

2022-08-23

（編輯 李冰）