基于點特征的直角坐標系空間直線度偏差評價
杜紅楓,陳曉航,王治忠,張乃方
(1.西安交通大學 科學與教育發展研究院,陜西 西安 710049;2.西安航天發動機有限公司,陜西 西安 710061)
0 引言
空間直線度偏差是指實際空間直線相對于理想空間直線的偏移變動量。在機械制造與檢測測量領域中,準確評價空間直線度偏差具有重要意義。在大尺寸軸、孔類零件的生產和加工過程中,受加工設備、加工方式的影響使零件產生空間直線度偏差,會直接影響產品的性能、壽命和質量。因此,建立一套符合直角坐標系下的空間直線度偏差測量與評價方法十分必要。
在前期開展的研究中[1-4],空間直線度偏差的定義與基本數學模型已被建立,為后續研究空間直線度偏差評價方法提供了良好的基礎。目前,空間直線度偏差評價方法分為幾何誤差建模方法和參數優化方法兩類。
幾何誤差建模方法依靠誤差模型的空間幾何關系建立偏差評價模型。文獻[5]提出了一種空間直線度坐標測量的不確定度計算方法,以保證空間直線度坐標測量結果的完整性和有效性;文獻[6]和[7]分別基于最小二乘方法提出了改進的空間直線度偏差評價模型,進而提高測量與評價的正確性。幾何誤差建模方法適用于數據量不大的情況,但是由于誤差模型與測量結果直接相關,精確建模難度較大。為了降低建模難度,提高計算精度,文獻[8]提出了一種基于切比雪夫范數的空間直線擬合模型,以提高軸線的擬合精度;文獻[9]至[11]提出了不同的基于幾何關系優化的空間直線度偏差線性逼近算法,在一定程度上提高了測量精度,但是計算效率有待提升。
參數優化方法的原理是將測量結果作為最優解進行尋優,本質上屬于非線性優化問題,適用于傳統數學計算難以處理的求解過程。文獻[12]和[13]給出了基于遺傳算法的空間直線度誤差評定方法,遺傳算法可解決幾何優化中存在的不足,但變量初始變化范圍及算法參數選取會在一定程度上影響結果的穩定性。為了提高計算效率,一些學者利用智能優化算法[14-15]處理測點擬合軸線的方向向量;也有一些學者研究了其它多目標優化算法,文獻[16]至[21]建立了空間直線度偏差計算模型,將非線性優化問題線性化處理。由于數據處理過程中,優化目標和核心尋優策略存在差異,導致參數優化方法在一些實際應用條件下計算效率較低。
為解決目前直角坐標系下空間直線度偏差評價方法建模難度大的問題,提出了基于點特征的直角坐標系空間直線度偏差評價方法。以直角坐標系下空間直線度測量法為研究對象,建立了空間直線度偏差評價數學模型。著重研究了空間直線度偏差測量模型、基于點特征的空間直線度偏差評價模型、基于點特征的空間直線度偏差最小區域評價方法,依托模型點特征關系,高效、準確地實現直角坐標系下的空間直線度偏差評價。最后利用三坐標測量機開展測量實驗,對該方法的可行性與準確性進行驗證。
1 空間直線度測量模型與數學模型
1.1 直角坐標系下空間直線度的測量模型
空間直線度偏差的測量模型由測量評價空間決定。截面測量法是圓柱體幾何量偏差最有效的測量評價空間模式[22],本文提出的空間直線度偏差測量模型建立在截面測量法的基礎上。如圖1所示,直角坐標系下空間直線度偏差測量模型由采樣、定心、擬合、評價四個部分組成,最后通過軸線的控制位置獲得空間直線度偏差測量與評價的結果。
1)采樣:在測量空間中通過測量儀器獲得被測圓柱體具體形貌的過程被稱為采樣,通過采樣獲得被測圓柱體位置參數,使被測圓柱體以數字形式復現。
2)定心:截面測量法可獲得多個截面輪廓的坐標數據,將截面輪廓坐標數據代入數學模型,可計算得出截面中心位置。計算獲得多個截面輪廓中心,從而真實客觀地獲取多截面的共有軸線。
3)擬合:對多個測量截面中心進行線性擬合,得到空間直線度偏差測量與評價基準—圓柱體中心軸線。中心軸線是實現坐標變換的基礎,也是圓柱體位置校正的基準線。
4)評價:在確定中心基準軸線后,需要對圓柱體中心軸線空間位置進行變換與投影。利用最小二乘法和最小區域法獲得包容軸線的圓柱半徑以對空間直線度偏差進行評價。
1.2 直角坐標系下空間直線度的數學模型
直角坐標系下空間直線度偏差的測量數據以笛卡爾坐標數據為主,這類數據由符合笛卡爾坐標系的測量儀器(如三坐標測量機、坐標投影儀等)獲得。根據直角坐標系下的空間直線度偏差測量模型,將被測圓柱體放置于直角坐標系內。在圓柱體上沿軸向方向均勻選取測量截面S1,S2,…Si(所有測量截面S均與儀器測量坐標系基準測量平面平行),測量截面數N≥ 5,i= 1,2,3,…N。每個測量截面的測量點數M≥ 5,各個測量點的坐標為Pij(xij,yij,zij),j= 1,2,3,…M。如果被測圓柱體零件軸向方向與Z軸平行,單一測量截面輪廓F(x,y)可表示為
F(x,y)=C1x2+C2y2+C3xy+x+C4y+C5(1)式中:C1,C2,C3,C4,C5為空間單一測量截面的輪廓系數。
為了降低計算誤差,將式(1)中x的系數設置為1。設置對稱矩陣A和B,根據單一測量截面的輪廓數據,利用最小二乘法計算截面輪廓系數。A和B的表達式為
則截面輪廓系數矩陣C為

其具體表達式為
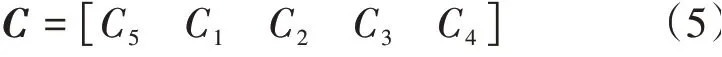
當獲得第i個截面輪廓系數C1i,C2i,C3i,C4i,C5i后,可得第i個測量截面中心坐標Poi(xoi,yoi,zoi),其中
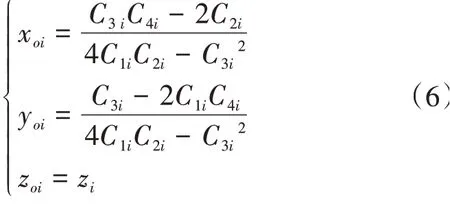
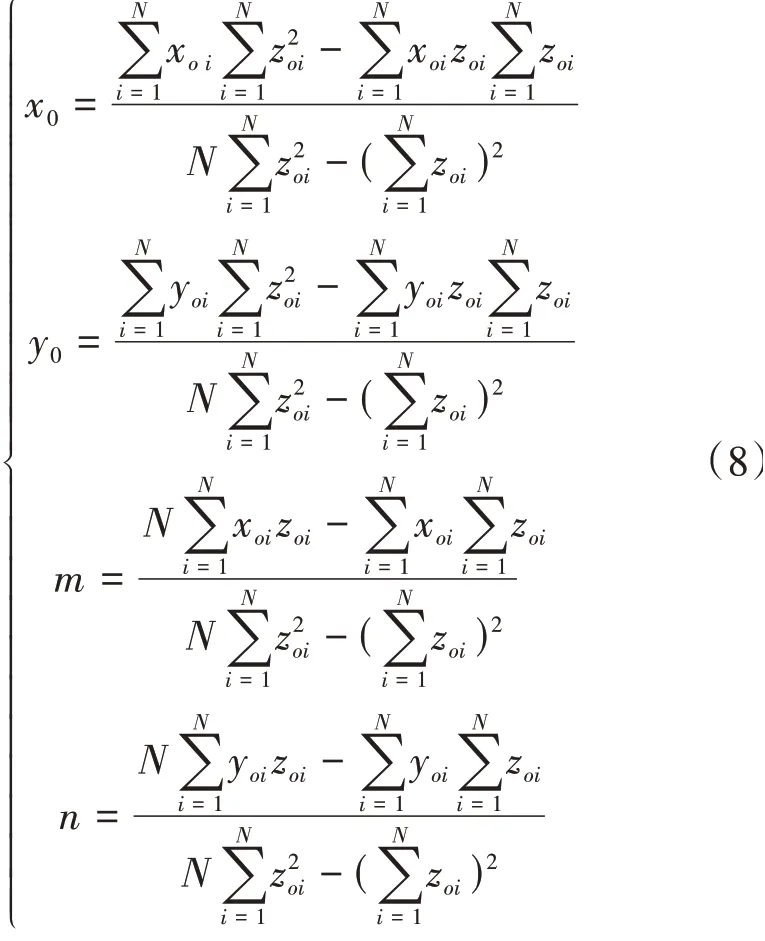
直角坐標系下空間直線度偏差評價模型的基礎是確定中心軸線位置。在截面測量法中,需要對多個測量截面中心進行空間擬合處理,從而獲得被測圓柱體的中心軸線。設圓柱體零件軸線的空間向量n=(m,n,1),x0和y0是空間軸線與XOY坐標平面的交點P0(x0,y0,0)的坐標,利用最小二乘法獲得被測圓柱體軸線的空間表達式為
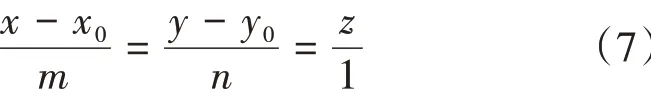
將被測圓柱體的多個測量截面中心用軸線相關聯,可獲得測量空間中被測圓柱體的軸線,如圖2所示。
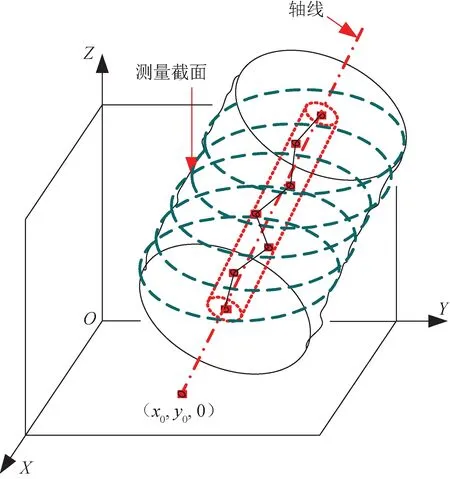
圖2 圓柱體空間軸線模型Fig.2 Model of spatial axis of cylinder
通過最小二乘法對多個測量截面中心進行擬合,可獲得被測圓柱體軸線表達式為
1.3 直角坐標系下測量空間中的統一
獲得了被測圓柱體的空間軸線后,需要對軸線及各個測量截面中心進行坐標轉化。坐標轉化的實質是將測量坐標系與工件坐標系統一,從而降低計算過程中產生的誤差,并提高模型計算效率。在直角坐標系下,坐標轉化包括坐標的移動和轉動。為了滿足測量坐標轉化的要求,以圖2中XOY坐標平面作為基準坐標平面,由此獲得的旋轉與平移組合轉化矩陣TXOY為
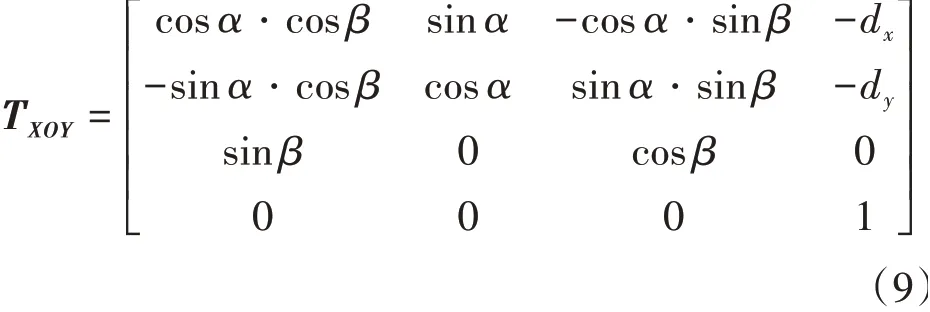
式中:α,β分別為軸線繞直角坐標系X軸,Y軸的旋轉角度,分別為坐標沿X軸,Y軸的平移量。
測量坐標轉換完成后,需要根據基準坐標平面對測量坐標值進行平面投影。以XOY坐標平面作為基準坐標平面,對應的投影轉化矩陣為
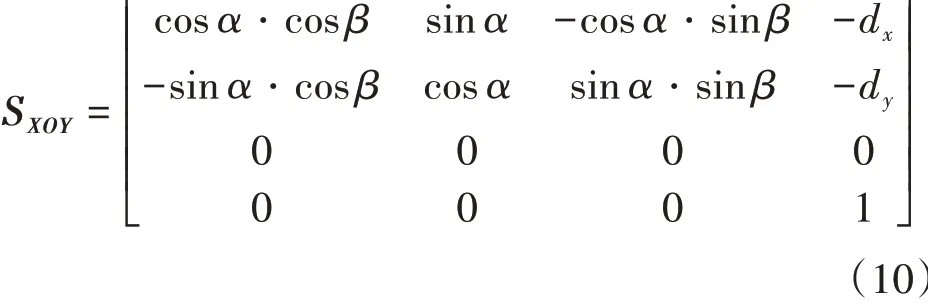
2 空間直線度偏差評價模型
利用多個測量截面中心的空間測量坐標在基準坐標平面的投影數據對空間直線度偏差進行評價,即確定截面中心投影數據的包絡區域。符合最小條件的空間直線度偏差為包絡被測圓柱體測量截面中心的最小的圓柱直徑,即空間包絡被測圓柱體軸線的最小圓柱的直徑。
2.1 空間直線度偏差最小二乘評價模型
設各個測量截面中心點到軸線的距離為Loi,則最小二乘空間直線度偏差SDLS為
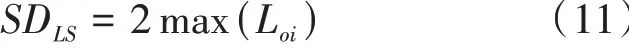
最小二乘空間直線度偏差評價模型由距離軸線最遠的測量截面中心確定,即“1+0”模型,該模型在投影面的結構如圖3所示。
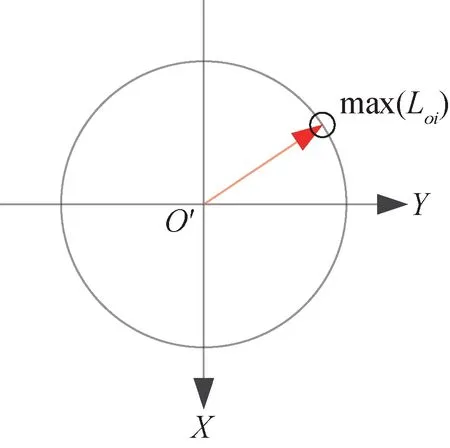
圖3 最小二乘空間直線度偏差評價模型Fig.3 Model of least square evaluation for spatial straightness deviation
“1 + 0”模型是指1個特征點必須在包絡所有測量截面中心的圓柱面投影輪廓上,即這個特征點距離軸線最遠。另外,在具有直角坐標系的測量儀器中,空間直線度偏差的測量應盡量滿足“小偏差、小誤差”條件。假設測量誤差足夠小,且可以降低被測圓柱工件軸線的位置誤差,為了降低測量誤差對測量結果的影響,采樣點數量應為偶數,且采樣點在測量路徑上應等間隔分布。
2.2 空間直線度偏差最小區域評價模型
最小區域空間直線度偏差是符合最小條件評定要求的。按照最小條件評定空間直線度偏差的本質是尋找最優的被測圓柱體空間直線位置,進而獲取Loi的最優解。由于空間直線度偏差模型為單一包容輪廓模型,參考圓柱度偏差的最小區域評價模型,空間直線度偏差最小區域評價中包絡被測圓柱體軸線的輪廓由2個點、3個點或者4個點構成,即“2 + 0”,“3 + 0”或者“4 + 0”模型,3種模型在投影面的結構如圖4所示。
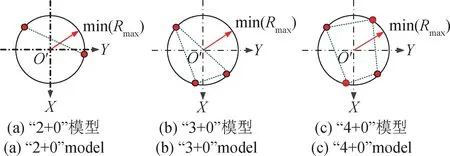
圖4 最小區域空間直線度偏差評價模型Fig.4 Models of minimum zone evaluation for spatial straightness deviation
在圖4中,“2 + 0”,“3 + 0”,“4 + 0”模型分別指2個、3個、4個特征點必須在包絡所有測量截面中心的圓柱面投影輪廓上,且這2個點、3個點、4個點構成的投影截面輪廓圓半徑R最小。三種模型均不存在內包絡圓柱面,因此無內包絡圓柱特征點,這與圓柱度偏差評價模型存在區別。“2 + 0”模型是“3 + 0”模型的退化形式,“4 + 0”模型是“3 + 0”模型的進化形式,三種模型中形成的包絡截面輪廓的最小外接圓直徑即為最小區域空間直線度偏差SDMZ,其表達式為
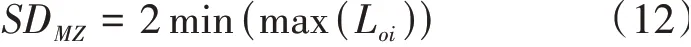
3 基于點特征的空間直線度偏差最小區域評價
基于點特征的空間直線度偏差最小區域評價建立在空間直線度偏差最小二乘評價的基礎上。基于點特征的最小區域評價由最小二乘評價模型演化而來。首先將被測圓柱的空間軸線和各個測量截面中心進行空間坐標轉化,之后以圓柱體軸線作為投影軸對測量截面中心進行投影,然后利用最小二乘方法獲得投影測量數據的軸心位置,并完成數據的初始處理。
在測量坐標系投影面上,通過投影點獲得被測圓柱體最小二乘中心軸線投影點Op后,以Op點為坐標原點對各測量點的坐標進行平移,獲得各點坐標值P'oi(x'oi,y'oi),然后依據各測點坐標構建空間直線度偏差最小區域評價模型。具體步驟為:
1)在投影平面內,從P'oi中找出距離Op最遠的采樣點M1(xM1,yM1),以及距離M1最遠的點M2(xM2,yM2)。
2)由M1,M2通過弦線截交關系中心V1(xV1,yV1)。由式(13)計算P'oi到V1(xV1,yV1)的距離,搜尋距離V1最遠的點M3(xM3,yM3)。
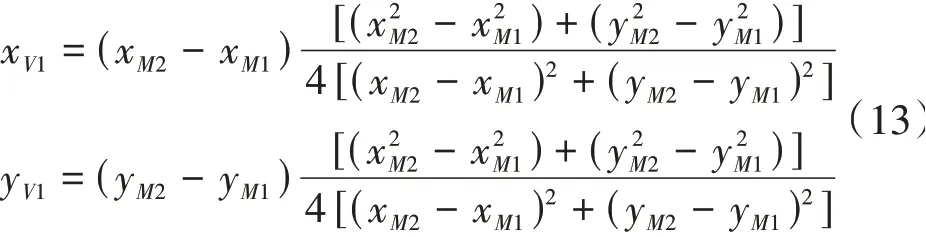
若|V1M3| ≤ |V1M1|,則M1,M2為“2 + 0”模型的特征點,空間直線度的偏差為2|V1M1|;若|V1M3| >|V1M1|,則M1,M3繼續通過虛擬中心迭代。
3)當M1,M2,M3迭 代 不 發 生 變 化 時,M1,M2,M3為“3 + 0”模型的特征點。通過3個點計算特征圓的圓心V2(xV2,yV2)的坐標為
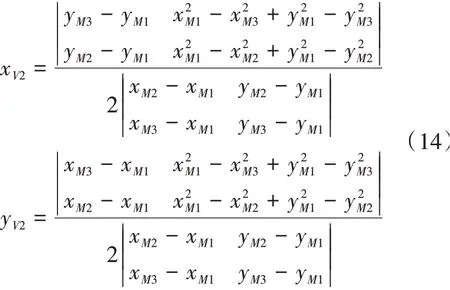
4)計算P'oi到V2的距離,搜尋距離V2最遠的點M4(xM4,yM4)。若|V2M4| ≤ |V2M1|,M1,M2,M3構成“3 + 0”模型,空間直線度偏差為2|V2M1|;若|V2M4| > |V2M1|,M1,M2,M4繼通過3個點計算特征圓的圓心進行迭代。
5)當M1,M2,M4迭代不發生變化時,M1,M2,M3,M4為“4 + 0”模型的特征點。通過四點計算特征圓的圓心V3,空間直線度偏差為2|V3M1|。由于空間坐標的特殊性,“4 + 0”模型實質是“3 + 0”模型的進化形式。
4 空間直線度偏差測量與評價的實驗測試與驗證
為了驗證基于點特征的直角坐標系下空間直線度偏差評價方法的有效性,結合實際測量件對研究內容進行驗證。測量對象為柴油內燃機活塞頭部(缸內導引面),需根據實測數據獲得活塞頭部形狀與輪廓誤差。利用HEXAGON Global Class SR 575型三坐標測量機來測量和評價活塞活頭部5 ~ 25 mm處的直線度偏差,要求空間直線度偏差控制在0.05 mm以內,測量截面采樣點數為400,測量截面數量為11個。實驗裝置如圖5所示。

圖5 實驗裝置圖Fig.5 Experimental setup
實驗中,三坐標測量機的最大允許誤差(MPEp)為2.3 μm,定位可重復性為0.5 μm,實驗室溫度條件為20 ℃。三坐標測量機測頭分別對被測活塞頭部圓柱面測量5次,測量結果如表1所示。由測量結果中可知:最小二乘空間直線度偏差為0.0276 mm,最小區域空間直線度偏差為0.0246 mm;被測活塞頭部軸線的X,Y方向向量接近于0,說明Z軸方向向量為1,證明坐標軸之間的誤差很小;最大測量相對誤差為1.5 μm,并且空間直線度偏差均小于0.05 mm符合要求,證明了基于點特征的直角坐標系空間直線度偏差評價方法的有效性與準確性。
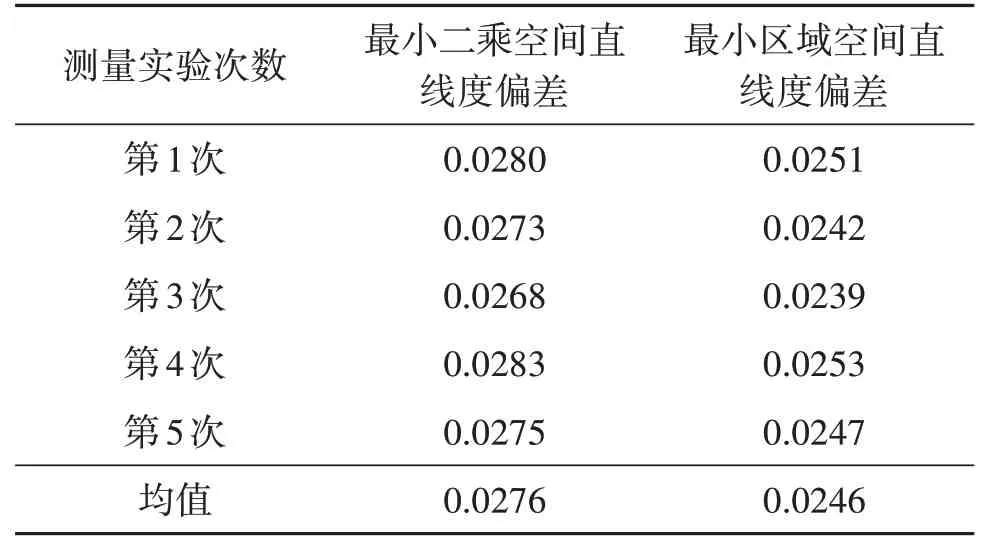
表1 活塞頭部空間直線度偏差測量結果Tab.1 Measurement results of spatial straightness deviation of the piston head mm
5 結論
在分析現有空間直線度偏差評價方法特點的基礎上,提出了基于點特征的直角坐標系下空間直線度偏差評價方法。根據評價模型的點特征關系,建立了直角坐標系下最小區域空間直線度偏差評價方法。重點研究了空間直線度偏差測量的數學模型,以及基于點特征的空間直線度偏差最小二乘和最小區域評價模型,有效降低了評價過程中的建模復雜度,提升了運算效率。該方法可廣泛應用于直角坐標系下圓柱體類零件的空間誤差測量領域,對于控制圓柱體類部件的加工質量具有重要意義。

