從“只見樹木”到“俯瞰森林”*
——解題教學案例

孔維娜 陳惠汝 冷 悅

（黃岡師范學院 湖北黃岡 438000）

一、背景信息

美籍匈牙利數學家喬治·波利亞（George Polya，1887-1985）為了回答“一個好的解法是如何想出來的”這個令人困惑的問題，專門研究了解題的思維過程，并把研究所得寫成《怎樣解題》一書。這本書的核心是分析解題的思維過程得到一張“怎樣解題”表，該表包括“了解問題”“擬定計劃”“實現計劃”和“回顧”四個步驟。波利亞曾說“掌握數學就意味著善于解題”，解題教學是中學數學教學的重要組成部分，它不僅是實現數學課堂教學目標的手段，而且對培養學生分析問題和解決問題的能力具有非常重要的作用。通過解題教學理論學習與教學實踐，能夠實現對數學及數學教學本質的進一步認識。

本案例源于一次模擬題，將其作為教學案例，是因為它突出了學生數學思維的訓練，全面滲透了波利亞“怎樣解題表”的過程，教學設計具有典型，具有推廣的價值。通過設計解題教學，解決了三角函數中一道看似無從下手的求余弦值題目。教師認為學生已經掌握了三角函數的性質、定理以及垂線的定理、向量的計算。但是學生對于題目中給出的垂線條件卻無法應用，于是出現了教與學思維不同步以及學生之間認知沖突的矛盾，經過教師的啟發式教學，學生將已有的概念進行整合，利用向量的數量積實現問題的轉化，不僅解決了這道問題，而且通過舉一反三，學生的數學思維得到進一步提升。

G老師任教于南京普通高中多年，教學經驗豐富。他的這節解題教學案例選用的是一次模擬考試，在考試結束后他發現有道題的檢測結果非常不理想，正確率只有9%。該題目顯示在△ABC中，已知是的垂心（三角形三條高所在直線的交點），，求cos∠BAC的值。

老師反思：為什么這么多的學生都不會做這道題甚至毫無頭緒呢？而關于三角函數的性質、定理，向量的計算都教過了，課后習題掌握的也不錯，但是學生為什么無法解出這道題呢？

教師通過合理地設計解題教學，有效地組織解題教學，可以發展學生的思維能力，提高他們的數學教學基本素養。基于此，老師發現波利亞的解題理論和這一題目相契合，因此編制了關于本題的解題教學設計。

二、案例正文

在上課前，G老師把測試卷發放到同學們手中，并和該題正確的學生進行了短暫的交流。上課開始的時候，G老師表明今天這節課的學習目標就是解決一道正確率極低的題，隨后，將本題寫到了黑板上，讓大家仔細審題。

【教學片段1】

1.已知和未知弄清楚了嗎？

師：請大家說說看，解題之前要做什么？

生1：明白已知和未知。

師：數學家波利亞曾經說過：“回答一個尚未弄清的問題是愚蠢的”。我相信大家都不愿意成為一個愚蠢的人，那我們先來看看這道題所包含的已知信息和未知信息有哪些？

生1：已知：

未知的是cos∠BAC的值。

師：已知的H和向量AH有什么特征？

生1：已知的H是△ABC的垂心且知道向量的關系式。

師：那你能從已知得到什么呢？

教師自評：在開展本次案例教學之前，我聽過幾位教師的同題講解，有的教師直接省略審題環節，對例題進行講解，節省了大把的時間，但不利于學生養成良好的解題習慣。因此，我毫不猶豫地帶領學生從審題環節入手，讓學生通過審題抓住題目中的關鍵信息，進而為解決問題打好基礎。

2.解題思維如何產生？

在完成初步的審題之后，G老師帶領學生進行解題方法的探索。

【教學片段2】

G老師給了同學們10分鐘獨立思考的時間。他在教室轉了一圈，發現大多數同學的狀態是緊鎖眉頭，仰視著黑板，沒有什么思路的樣子。個別同學在紙上寫出了一些關系式，根據關系式得出了一個式子，但大多數同學止步于此，再無其他進展。G老師便開始詢問同學們在解題的過程中遇到了哪些困難？好多同學反映：結論要求cos∠BAC就需要知道△ABC中邊角關系，將兩邊平方，平方后雖然出現了cos∠BAC，但也出現了無法處理，也就沒辦法解題。這時，G老師啟發學生們將各種數學知識聯系起來。

師：這道題考察什么樣的方法，源頭在哪里？教材中有沒有此類方法的例子？大家找找看課本中是否有這樣的例子。同學可以小組合作。5分鐘過后，G老師請各小組代表匯報本組的討論進展。

組1：回歸教材（蘇教版）必修5第13頁余弦定理的證明。教材中對向量等式兩邊平方證得余弦定理。我們這個方法，將兩邊進行了平方，卻沒有辦法做下去。

在這里教師詢問1組的學生，那么你們有什么條件沒有用到呢？是不是一定要平方才能得到邊角關系呢？在教師的提問下，其他小組得到了啟發。

組2：小組2在教師的啟發下，回歸教材（蘇教版）必修5第6頁正弦定理的證法2，在△ABC中，不妨設∠C為最大角，過點A做AD⊥BC于D。

師：大家找的都很好，我們通過對余弦定理和正弦定理的回歸學習，理解了“向量的數量積是將向量等式轉化為數量等式的常用工具”。同時發現原題目中H是△ABC的垂心這一條件，可以將向量關系轉化為數量關系解決問題。請各小組繼續討論，數量積應該怎么轉化？

2.鐘后，小組3的同學們舉手，躍躍欲試，G老師請他們分享結果。

組3：老師，我們可以利用H是△ABC的垂心這一條件，知道，同理我們可得，通過兩個垂直的條件利用數量積的轉化可得出cos∠BAC的值。師：很好，請說出你的推導過程。

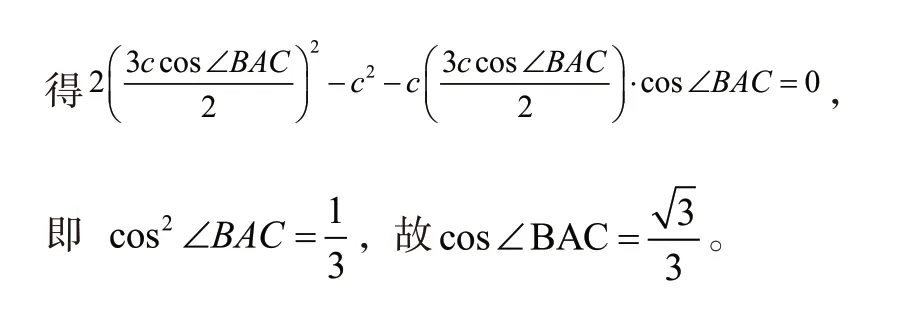
師：這個解法很漂亮。那是怎么想到的呢？

組3：我們就是根據回顧的正弦和余弦定理的證明過程得知的，通過把向量積的問題轉化為數量關系，進而求出∠ BAC 的余弦值。

師：一個好的解題方式就這樣產生了，哪個同學愿意分享一下自己的收獲呢？

生2：在解題思路的探索過程中，我發現了轉化思想的重要性，將一個未知的問題轉化成自己所學過的知識，降低解題的難度。另外，通過本題的學習，我還知道好的念頭是解決成功的法寶，在本題中數量積是很有用的一個工具。

師：這位同學總結得很好。

教師自評：“H是△ABC的垂心”這個條件怎么用是解決這個問題的關鍵所在。在整個解題的過程中，我覺得解題的目標重在引導學生學會如何思考構建數學思維是非常重要的，強調轉化思想更為重要。只有將已學的各個部分有機地聯系起來，才能夠成功地將題目中的已知條件轉化，即形成初步的數學思維，使問題迎刃而解。波利亞告訴我們：“一個好念頭的基礎是過去的經驗和已知的知識，僅僅到記憶不足以產生好的念頭。”因此，我覺得鼓勵學生將已有知識和現有的知識連接起來是很重要的。

3.解題計劃的實施過程

與同學們一起制定解題計劃之后，G老師安排生3到黑板上書寫解題過程，并要求其他同學在草稿紙上完成。

【教學片段3】

師：請大家看黑板，說一說生3的解題過程是不是很完整？

生4：他在計算時，雖然將兩種情況都寫了出來，但是沒有將兩個結論聯系起來，故沒有得出的余弦值。

師：那我們應該怎么解決這個問題呢？

生5：應該將（2）中得出的結論代入到（1）式中才能得出正確的結論。

師：數學是一門非常嚴謹的學科，相較于其他學科，數學對人的考驗更大。在條件不充分的情況下就不能下結論，具有整體的聯系觀念也是非常重要的。如果解題不規范，就不能算是完整的解題。通過這一點，波利亞告訴了我們，相比擬定解題計劃，實施計劃要容易得多。但在這一過程中，最主要的就是耐心！耐心寫出每一步，確保每一步計算的準確性，而且要學會將解出的答案進行前后聯系。

G老師利用實物投影儀展示了其他四個同學的解題過程，對他們的解題過程進行了評價，對他們忽略的細節進行補充。

教師自評：在解題的過程中，學生認為對問題有了解題的思路且算出結果就是完成任務了。但是他們對解題過程的規范性卻不夠重視，常常出現會做的題目拿不到滿分的情況，或是因為書寫問題導致失分現象嚴重，這些都不利于學生數學素養的培養。因此，我覺得解題教學中的書寫環節是非常重要的，要求學生必須在黑板上或者筆記本上規范的寫出解題過程，進而及時的發現他們的錯誤進行糾正，讓他們產生深刻的印象。解題計劃的實施是培養學生嚴謹性的重要環節，是不能忽視的。

4.反思過程是必要的嗎？

完成了前面三個教學環節之后，解題回顧與反思還有必要嗎？老師通過下面的教學片段充分體現了回顧和反思在解題教學中的重要性。

【教學片段4】

師：請大家先不要收起草稿本，你們有沒有在解題結束之后回頭再看看解題過程呢？也許你會有意想不到的發現。

（聽到老師發問之后，同學們一個個瞪大了雙眼，在同學寫的解題過程中尋找。）

生6：老師，我發現這道題很典型，知道∠BAC的余弦值，如果再給定一個條件，關于正弦的，也可以求出它的正弦值，知道正弦值和余弦值之后，同樣也可以得出正切值。

師：很好，我發現同學們真正的掌握了這節課所要達到的目標。

生7：老師，我發現只要是與向量有關，均可將向量積轉化為數量積，將復雜的數學問題轉化為簡單的問題。

師：是不是很有趣？你有什么感悟呢？

生8：很多題目之間都是有關聯的，舉一反三的思維是非常重要的。

師：是的。當我們做完一個題目后，一定要學會檢查與回顧，解題的最大收益不在于做的題多，而在于質量，“題海戰術”是我們現在最不提倡的。

教師自評：在教學的過程中，很多老師往往最容易忽略的是檢驗與回顧。波利亞在《怎樣解題》中指出：解題“最重要的那部分就是回去再看一下完整的解答”，解題教學的舉一反三是必要的。