磁力耦合機電產品電磁-結構多場聯合仿真方法研究
蔣圣鵬,唐曉峰,李佳圣,侯如非,王藝偉
(上海機電工程研究所,上海 201109)
磁力耦合機電產品被廣泛應用于工業、裝備等領域,其機電特性研究是設計應用的基礎。目前對于磁力耦合機電產品的研究可分為解析法、動力學仿真和電磁仿真。陳興球[1]應用靶板變形理論和經典力學方法計算了激活機構的撞擊能量與熱電池底部激活部分厚度的關系,試驗結果表明該方法具有較好的準確性;梁東升[2]進行了引信電源旋轉撞擊和翻轉限制機構的動力學仿真,仿真結果證明了激活裝置可有效激活熱電池;朱春暉[3]基于Maxwell 軟件對磁后坐能源進行了電磁仿真,得出了各個尺寸大小與電源的感應電動勢和功率的關系曲線,并用于指導激活機構的設計。孔超等[4]通過多體動力學仿真進行了某導彈電磁彈射裝置的發射穩定性分析,驗證了電磁彈射技術在某型導彈發射上應用的可行性。楊毅鈞等[5]通過Maxwell二維和三維電磁仿真試驗,進行激活器銜鐵構型的優化,并通過試驗驗證了該方案的可行性。
以上對于磁力耦合機電產品的研究均通過單一場的計算完成,但磁力耦合機電產品中的電磁-結構耦合特性較為復雜,單一場仿真無法充分反映產品電磁-結構耦合工作特性,需進行電磁-結構多場聯合仿真。
本文以激活裝置為研究對象,提出了一種帶扭簧蓄能機構的激活裝置,基于麥克斯韋電磁場方程和結構動力學方程計算并分析激活裝置輸出電壓及其影響因素。通過電磁-結構多場聯合仿真計算激活裝置磁力參數和輸出電壓,測試激活裝置性能,搭建測試系統并獲取激活裝置輸出電壓,驗證磁力耦合機電產品中的電磁-結構多場聯合仿真計算方法的準確性。
1 研究對象
本文提出了一種帶扭簧蓄能機構的激活裝置如圖1所示,由激活扳手、主動軸、蓄力扭簧、激活器等組成。其中激活器又包括從動軸、銜鐵、永磁體、線圈等,結構如圖2所示。
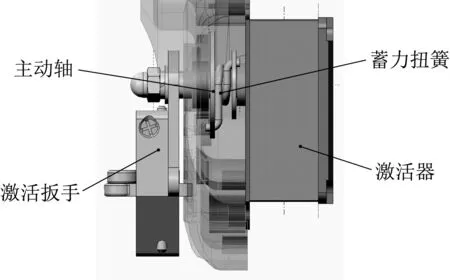
圖1 激活裝置Fig.1 The activation device
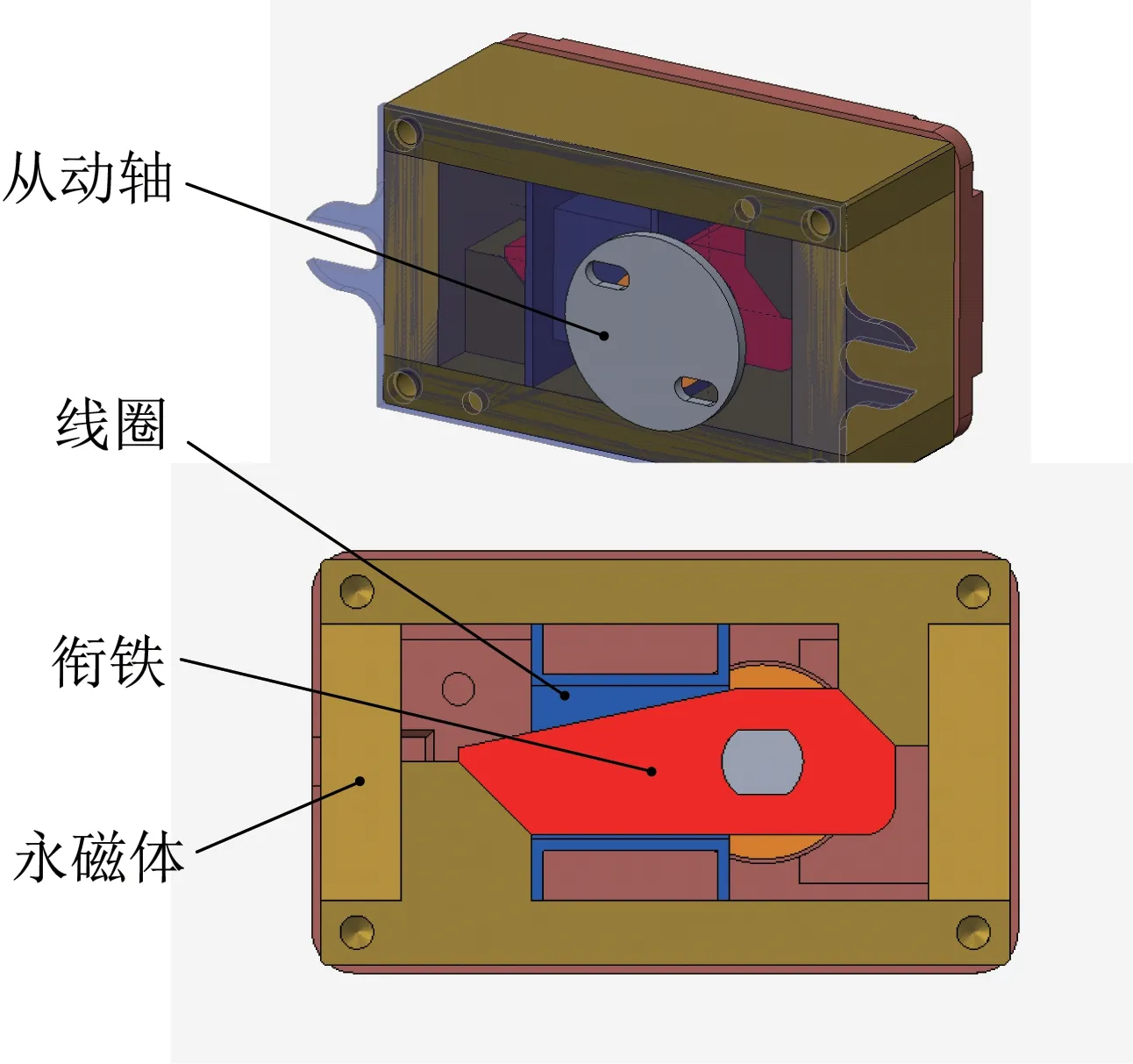
圖2 激活器結構Fig.2 The structure of activator
蓄力扭簧兩端分別插入主動軸和從動軸中,通過扣動激活扳手使主動軸轉動,與從動軸產生位移差,隨著位移差的增大蓄力扭簧持續蓄力,當蓄力扭簧的轉矩大于永磁體對銜鐵的磁力矩時,扭簧將銜鐵高速彈開,激活器磁路變化使穿過線圈的總磁通量發生變化,產生感應電動勢。該裝置依靠蓄力扭簧提升激活瞬間銜鐵轉動速度和速度的一致性,保證了激活裝置電壓幅值和電壓輸出的一致性。
2 研究方法
2.1 電磁-結構仿真理論
基于麥克斯韋方程組進行激活裝置電磁計算[6],即
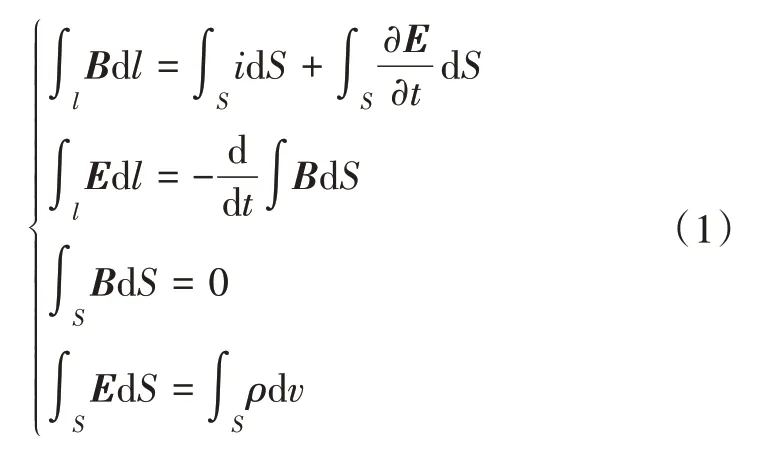
式(1)中,B為磁場強度;S為線圈截面積,i為經過環路曲面的電流;E為電場強度;ρ為電荷。
根據式(1)中的第二個方程,激活器線圈兩端電勢差為

式(2)中,V為感應電動勢;E為電場強度;N為線圈匝數;B為磁場強度;S為線圈截面積,ω為銜鐵轉動角速度;α為轉角。
考慮電路線阻,激活器輸出電壓作用于火工品的電壓為
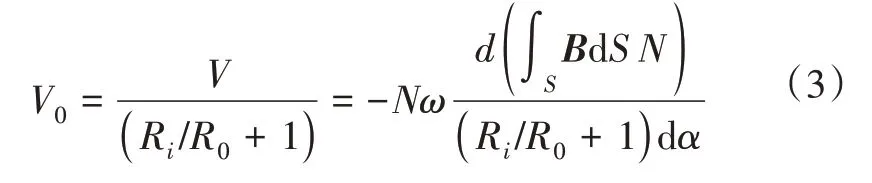
式(3)中,V0為火工品兩端激活電壓;Ri為線圈內阻;R0為火工品阻值。
激活裝置磁力大小可由麥克斯韋電磁力公式計算[7],即

式(4)中,φ為工作氣隙磁通;μ0為真空磁導率。
激活裝置全工作流程可分為兩個階段。
第一階段:激活扳手以角速度ω繞軸勻速轉動,磁力矩(Tm)克服銜鐵偏心重力矩(Tg)和扭簧彈力矩(Ts),使銜鐵吸附在側板上。激活裝置各項參數如下所示:

式(5)中,α為激活扳手轉角,β為銜鐵轉角,k為扭簧剛度。
第二階段:扭簧彈力矩Ts>Tm0+Tg,銜鐵彈開并加速運動。加速過程可由動力學方程描述,即
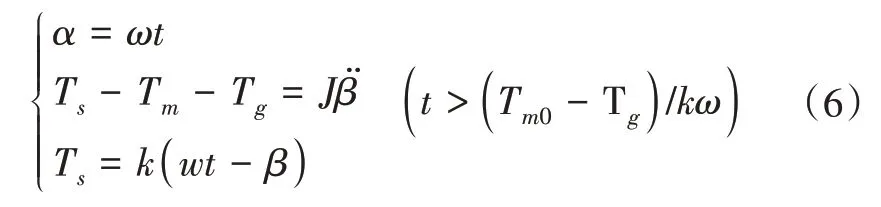
式(6)中,磁力矩Tm隨銜鐵轉角變化而變化,可通過式(4)計算得到;銜鐵轉速和轉角可通過計算動力學方程如式(5)和(6)求解;線圈磁通量與銜鐵轉角有關,因此,可將銜鐵轉角作為式(2)的輸入計算激活裝置輸出電壓。
2.2 電磁仿真建模
在激活裝置三維電磁有限元建模前,為了便于仿真計算,對模型進行了合理簡化:
(1)線圈中單根導線橫截面積較小,忽略渦流產生的不均勻效應;
(2)模型材料各向同性,可忽略磁滯的影響;
(3)計算參數均為25℃下的標準值,忽略磁導率和電導率受溫度影響。
基于以上假設,進行激活裝置三維電磁有限元建模,保留主磁路元件,包括永磁體、兩個側板和銜鐵。其中永磁體材料為 N48H 釹鐵硼,剩磁Br≥13.49KGS;矯頑力Hc≥1032KA/m;磁能BHmax≥349.9kJ/m3。銜鐵和左右側板材料為電工純鐵DT4E,矯頑力Hc≤48KA/m;矯頑力時效增值ΔHc≤4.8KA/m;最大磁導率μm≥0.0113H/m。
求解類型選定為靜磁場求解,激勵由永磁體提供,無需額外設置,指定模型邊界,將空氣界面法線方向磁感設為0。為了研究磁力矩隨銜鐵角度的變化情況,將銜鐵角度變量設置為0~20°,步長為0.1°,最終得到三維電磁仿真模型如圖3所示。

圖3 激活裝置三維電磁仿真模型Fig.3 Electromagnetic simulation model of the activation device
2.3 動力學仿真建模
在電磁仿真模型的基礎上,建立動力學模型。將電磁仿真中的磁力矩-角度計算結果以Spline 的形式輸入Adams,在Adams 軟件中建立激活裝置的動力學仿真模型,如圖4所示。

圖4 激活裝置動力學仿真模型Fig.4 Dynamic simulation model of the activation device
扳手、銜鐵和轉軸添加鉸鏈約束,銜鐵上施加順時針方向磁力矩,磁力矩隨角度變化情況通過電磁仿真得到。銜鐵與連桿之間定義扭簧,激活扳手以5(°)/s的角速度逆時針勻速轉動。激活裝置蓄力角α0=10°,扭簧剛度k=80N · mm/(°),預緊力=400N · mm。
3 電磁-結構仿真結果
基于麥克斯韋電磁場方程,建立激活裝置磁場得到磁場強度云圖和磁力線分布如圖5所示,磁力矩隨角度變化情況如圖6所示。激活裝置處于靜平衡位置即銜鐵角度為0時,激活裝置磁力矩為0.83 N·m。隨著銜鐵角度增大,磁力矩逐漸減小。
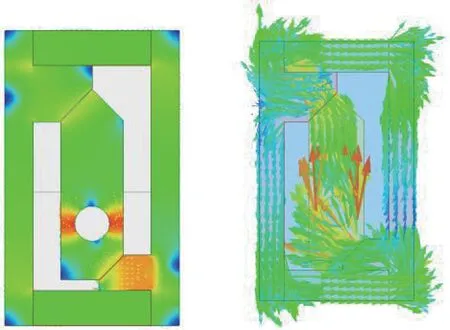
圖5 激活裝置磁場強度云圖Fig.5 Magnetic flux density of the activation device

圖6 激活裝置磁力矩-角度關系曲線Fig.6 Magnetic moment curve of the activation device
將電磁仿真得到的磁力-角度值作為動力學仿真的輸入,對激活裝置進行動力學仿真,得到仿真計算結果如圖7所示,結果表明當激活扳手以5(°)/s 的角速度勻速轉動,銜鐵在0~1 s 靜止不動,這是由于銜鐵所受磁力矩小于扭簧彈力矩,銜鐵被緊緊吸住。當彈簧壓縮量達到10.4°后,銜鐵所受彈力矩大于磁力矩,銜鐵脫開并進行加速運動,銜鐵運動10°后,彈簧彈力矩與磁力矩平衡,銜鐵開始隨連桿一起以5(°)/s 的角速度勻速轉動。銜鐵脫開瞬間由于扭簧彈力矩作用,銜鐵將會以最大3043(°)/s的速度切割磁感線。
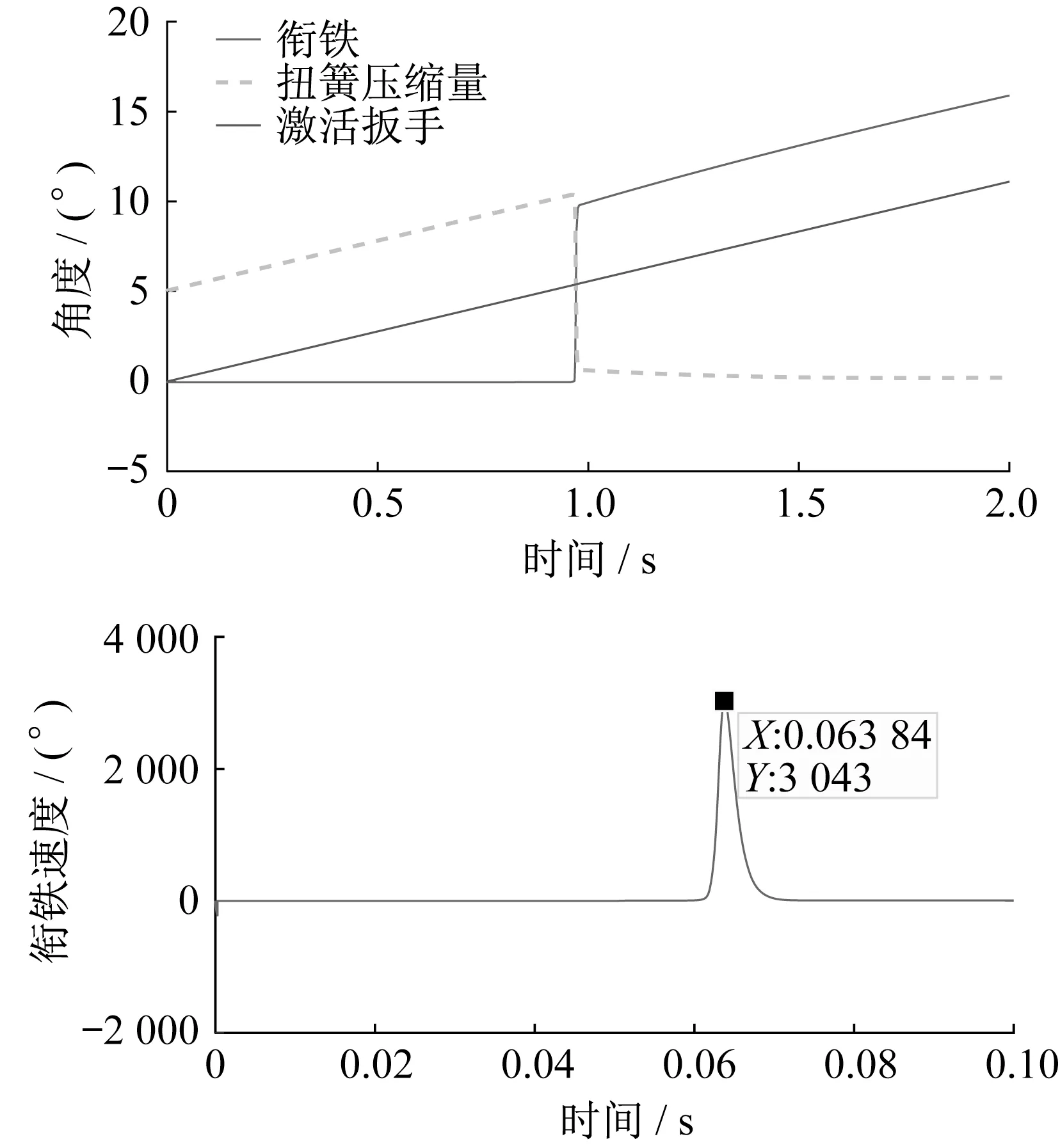
圖7 動力學仿真結果Fig.7 Dynamic simulation results
將動力學仿真計算得到的銜鐵角度-時間關系θ=f(t)代入電磁仿真計算的磁通-角度關系F=f(θ)中,可求得激活裝置磁通隨時間變化的曲線,如圖8所示。通過式(3)可計算激活裝置輸出電壓,如圖9所示。仿真結果表明,銜鐵脫開瞬間通過線圈的磁通發生突變,根據電磁感應原理,線圈產生較大電壓,最大電壓可達1.95 V。

圖8 激活裝置磁通量-時間關系曲線Fig.8 Magnetic flux-time curve of the activation device
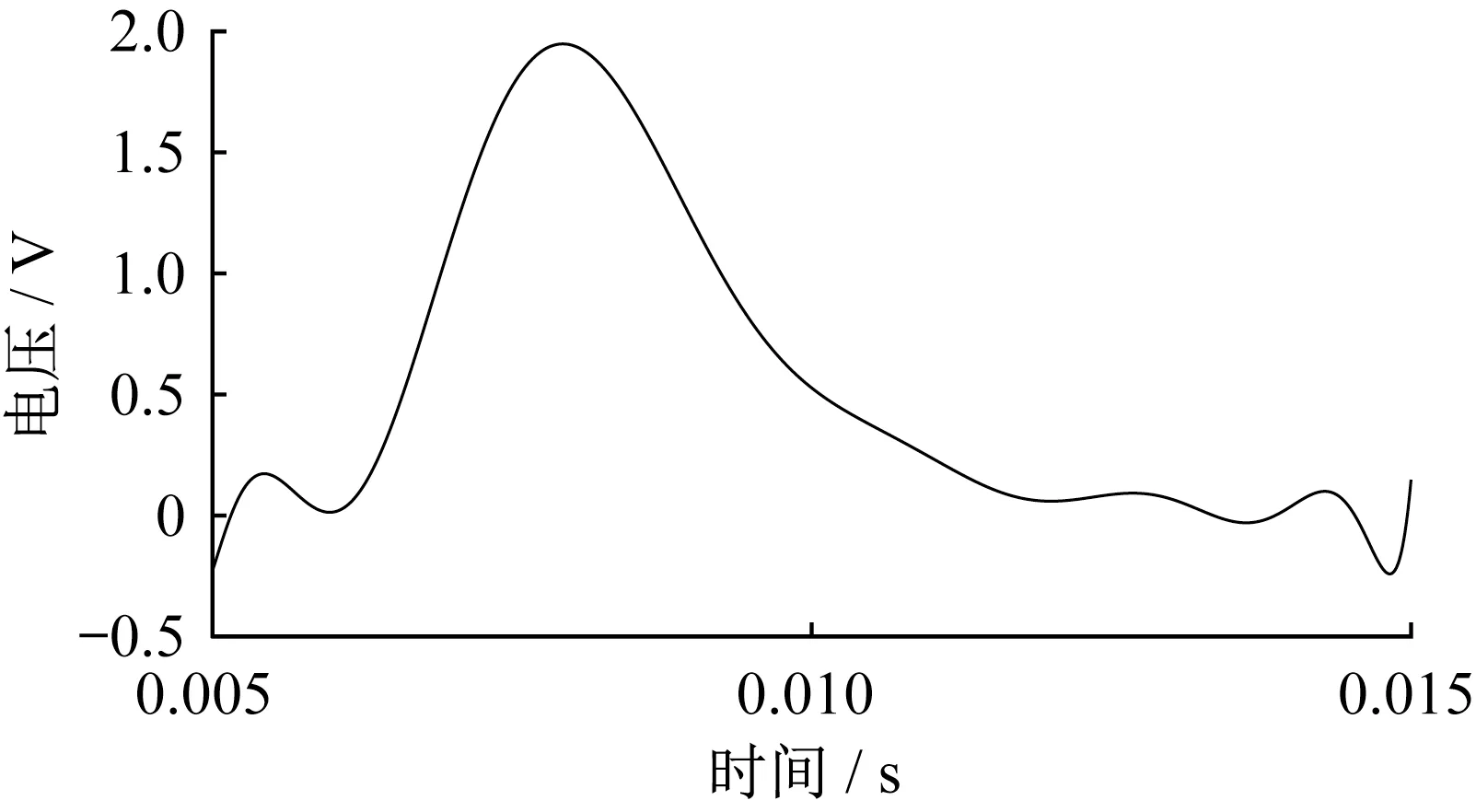
圖9 激活裝置輸出電壓-時間關系曲線Fig.9 Voltage-time curve of the activation device
4 激活裝置性能測試驗證
為驗證激活裝置輸出電壓,對激活裝置進行磁力矩和輸出電壓測試。磁力矩測試時,在激活器輸出軸上增加轉接力臂工裝,使用推力機推動轉接工裝,根據脫開瞬間推力機推力換算得到磁力矩。在進行輸出電壓測試時,根據如圖10(a)所示的電路原理圖搭建測試電路如圖10(b)所示,其中激活器作為電源,1 Ω 電阻作為火工品模擬負載,示波器用于測試負載的脈沖電壓-時間關系。
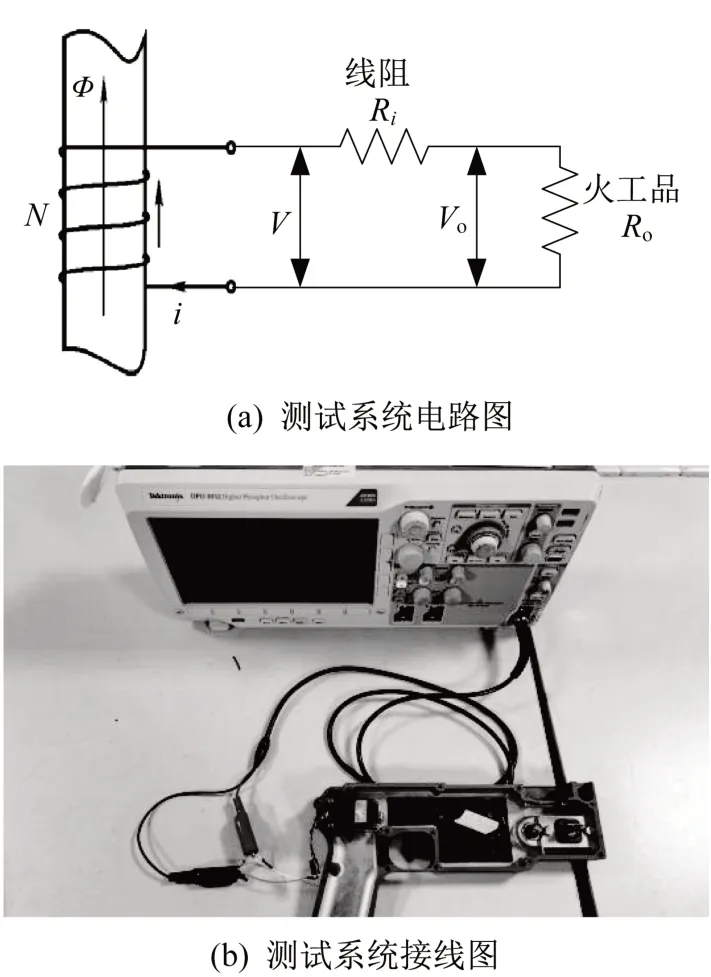
圖10 輸出電壓測試系統Fig.10 Output voltage test system
通過激活裝置磁力矩和輸出電壓測試,得到測試結果如表1所示。磁力矩仿真計算誤差為4.65%,輸出電壓仿真計算誤差為2.60%,仿真與試驗結果誤差在5%以內,驗證了仿真方法的準確性。
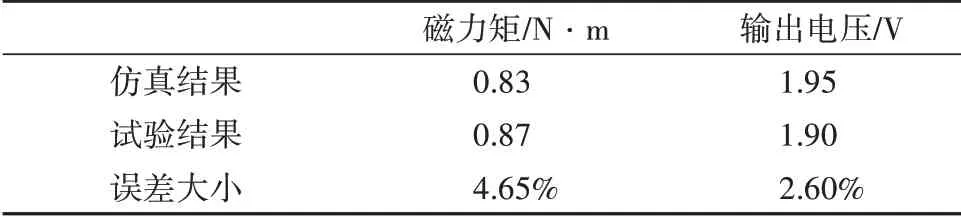
表1 激活裝置測試結果Tab.1 Test result of the activation device
5 結 論
為充分反映機電產品電磁-結構耦合工作特性,本文提出了一種電磁-結構多場聯合仿真方法。基于麥克斯韋電磁場方程和結構動力學方程分析了激活裝置輸出電壓及其影響因素,構建電磁-結構多場聯合仿真模型并開展仿真計算方法研究,最后通過激活裝置電壓測試驗證計算方法的準確性。得到結論如下:
(1)本文所述的電磁-結構多場聯合仿真方法可充分反映磁力耦合機電產品的工作特性,獲取產品的電磁參數和動力學參數。
(2)電磁-結構聯合仿真方法具有較高的計算精度,與試驗測試結果對比誤差可控制在5%以內。
本文提出的電磁-結構聯合仿真方法對磁力耦合機電產品性能研究具有參考價值。

