大面積超薄蒸汽腔力學特性仿真分析
聶曉展,程 鑫,王珊珊,李春煜,楊 光*,吳靜怡
(1.上海交通大學制冷與低溫工程研究所,上海 200240;2.上海衛星裝備研究所,上海 200240)
如今,隨著電子技術的快速發展,電子設備中元件的集成度越來越高,使得設備的單位面積發熱功率逐漸增大。研究表明,電子器件表面的平均熱流密度已達到100 W/cm2以上,局部表面的熱流密度更高[1]。發熱功率的增大將導致電子器件工作溫度顯著提高,而工作溫度過高是電子器件失效的最主要原因之一,其失效率隨著工作溫度的升高呈指數增長趨勢[2]。因此,為保證電子器件高效、穩定地運行,必須利用有效的散熱技術防止過高的工作溫度。解決高熱流密度散熱的首要問題便是如何把集中的熱源快速擴展至大面積表面進行冷卻[3]。
在平板熱管的基礎上,可實現高效徑向熱擴散的蒸汽腔逐漸被廣泛關注,其工作原理為:熱源與蒸汽腔的蒸發側直接接觸,蒸發側毛細芯內的液體工質吸收熱源輸入熱量蒸發形成蒸汽,壓差驅動蒸汽在空腔內迅速擴散,并在另一端冷凝側釋放潛熱后凝結成液體。冷凝過程中釋放的熱量可由外部冷卻如自然對流或輻射換熱帶走。冷卻下來的液體工質沿著內腔吸液芯和支撐柱表面的毛細結構回流到被加熱區,從而形成工作循環。因此,良好的溫度均勻性、高效的熱擴散能力是蒸汽腔的顯著優勢,這為解決航空航天一些高功率電子、光電器件的迫切散熱需求提供了一種具有前景且有效的解決方案[4]。
目前對蒸汽腔的研究主要集中于優化蒸汽腔內毛細結構,提高液體輸運效率。Ranjan 等人[5]對毛細芯結構中薄膜蒸發的微尺度模型進行了研究,分別對4種不同幾何形狀的毛細芯進行了建模,并對其蒸發性能進行了比較。Lurie 等人[6]對蒸汽腔內燒結芯體最佳幾何形狀的拓撲優化方法進行了數值模擬研究,研究表明采用最佳形狀的毛細芯可提高蒸汽腔的運行性能,最大可將其傳熱能力提高到具有恒定厚度毛細芯的蒸汽腔的兩倍。Peng等人[7]提出并研究了生物形態葉形結構毛細芯;Hwang等人[8]研發了多動脈蒸汽腔。結果均表明,使用上述特殊幾何形狀的毛細芯降低了毛細芯對水的阻力,從而可以向蒸發器區域提供更快速的液體回流。
除毛細結構以外,蒸汽腔中另一關鍵結構是支撐柱。蒸汽腔中的支撐柱主要起到承力以及增加額外的液體回流通道2 個方面的作用[9]。針對蒸汽腔內的支撐柱,大多研究的關注點是支撐柱作為液體回流通道時對蒸汽腔總體傳熱性能的影響。Min等人[10]研究了直徑為5 cm 的圓形蒸汽腔,通過理論推導發現,隨著蒸汽腔內支撐柱半徑的減小,蒸汽腔總熱阻也會下降,但是由于支撐柱表面的微結構需要提供足夠的毛細力來防止液體阻塞,故支撐柱的半徑存在一個最小值。Hwang 等人[11]通過實驗發現,相比于無支撐柱的蒸汽腔,多支撐柱蒸汽腔具備明顯的低熱阻、高熱流密度的特點。Hsieh 等人[12]通過分離變量,給出了有無支撐柱情況下,腔體內溫度分布的三維解析解,并從蒸汽擴散阻力角度,考察了2 種情況下,蒸汽腔的傳熱性能變化。
隨著航天技術的發展,電子元件尺寸和功率的增大導致蒸汽腔散熱面積的增大,而外界環境的真空和較高的散熱元件溫度,會使大面積蒸汽腔產生相比于在地面工作條件下更大的內外壓差和變形。所以,保證蒸汽腔整體的力學性能尤為重要。目前,與蒸汽腔力學性能相關的定量規律仍不明確。因此,本文將從腔體結構出發,通過各結構參數對腔體最大應力的影響,探究腔體各結構參數對其力學性能的影響規律。
1 研究方法及理論依據
大面積超薄蒸汽腔的散熱面積可達1 平方米以上,而厚度僅為幾毫米,內部支撐柱呈規律性周期分布。如果采用整體建模,將導致計算量過大,并且由于蒸汽腔在水平厚度方向和垂直厚度方向上尺度的差異,網格很難捕捉微觀特性,從而不能保證仿真精度,故采用局部建模的方法,通過局部性能預測整體性能。在力學中,針對這種宏觀尺度較大且微觀結構具備周期對稱性的研究對象,通常采用代表體元法(Represents volume element method,RVE)。
1.1 代表體元法
代表體元法通過分析結構微觀尺度的力學性能,預測宏觀尺度下結構的力學性能,可以在保證計算精度的前提下,快速建立有限元分析模型,減少計算時間[13-14]。代表體元法是基于整體結構漸進均勻化以及周期性邊界條件的前提下提出的。隨著單位面積支撐柱數量的增多,支撐柱間距變小,腔體內不同位置支撐柱的應力分布趨于一致。此時,研究單個支撐柱的應力分布等效于蒸汽腔所有支撐柱的應力分布。圖1(a)為代表單元示意圖,其中d為支撐柱直徑,h為底板板厚,圖中A1為支撐柱橫截面積,A2為正六邊形總面積,(A2-A1)/A2為孔隙率,取為ε。在圖1(b)中,分別進行了蒸汽腔的整體建模和局部建模。對比兩者可發現,其應力分布一致,并且最大應力僅相差8%。
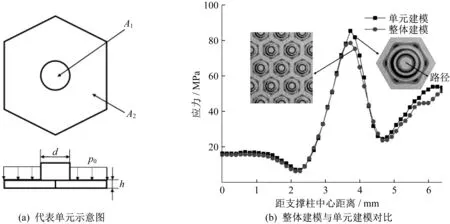
圖1 不同建模方法的對比Fig.1 Comparison of different modelling methods
1.2 力學建模基礎
在彈性力學中,當薄板受到一般載荷時,總可以把每一個載荷分解為2 個分載荷,一個是作用在薄板中面之內的所謂縱向載荷,另一個是垂直于中面的所謂橫向載荷[15]。顯然該模型所受載荷為橫向載荷,它們所引起的應力,形變和位移可以按薄板彎曲問題求解。
對于正n邊形薄板的小撓度彎曲,當n無限大時,模型趨近于圓形薄板,所以可以參考圓形薄板的軸對稱彎曲。
極坐標下彈性曲面微分方程為
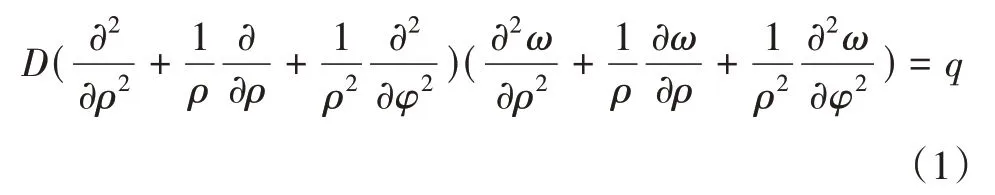
當橫向荷載q=q(ρ),撓度ω=ω(ρ)時,式(1)可簡化為
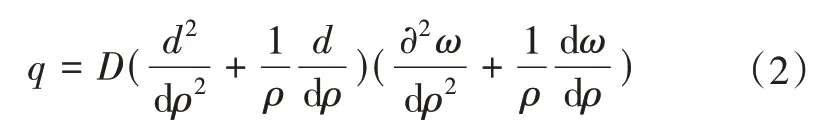
對式(2)積分4 次,便得到軸對稱彎曲問題的撓度解答,即
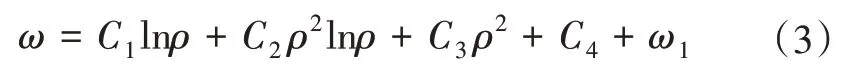
對于受均布荷載q=q0的薄板,特解
代入邊界條件可解得C1、C2、C3、C4,進而得到ω的表達式。
極坐標下薄板內力公式為
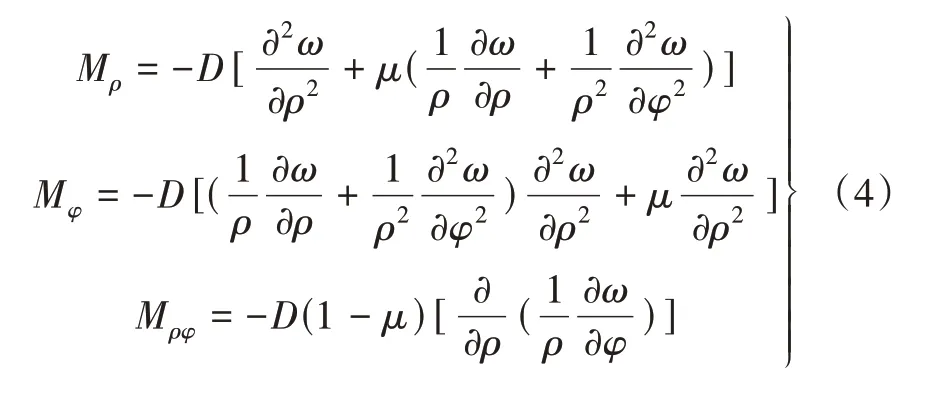
對于任意一點應力,有
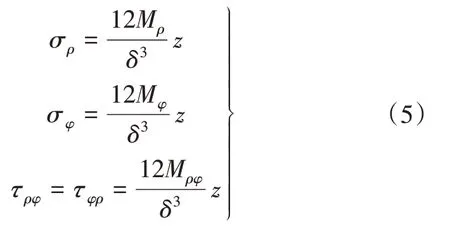
通過以上分析,對于周邊固定圓形薄板受均布荷載q0的情況,應力情況為
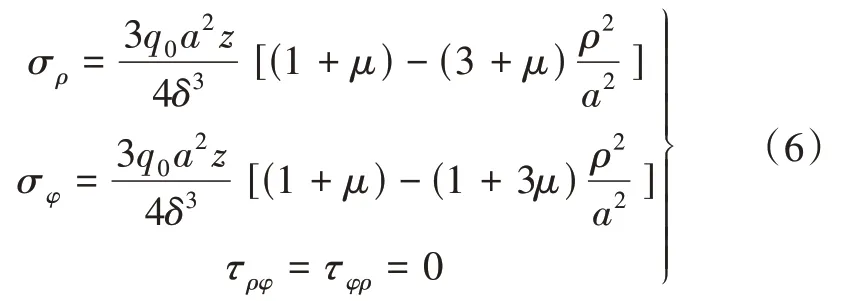
其中,a為圓形薄板的半徑,δ為板厚,μ為材料的泊松系數。
1.3 有限元仿真方法
有限元仿真是力學分析中的常用方法。對于代表單元仿真模型(圖1(a)),設置正六邊形周邊邊界和支撐柱上表面為對稱邊界條件,上板面施加均布荷載q0=8 MPa,由于支撐柱與板面連接處會產生應力集中,在連接處設置1 mm 的對稱倒角。材料為6061 鋁合金。采用控制變量的方法,分別選取不同的支撐柱直徑d、孔隙率ε、板厚h和均布荷載q0,依次判斷各變量對單元體最大應力σMAX的影響。
由于本文代表單元模型結構的特殊性,無法通過解析解進行仿真精度校驗,故需建立合理的驗證模型。正n邊形與圓形有一定相似性,且n越大,相似性越高;代表單元模型中支撐柱與底部薄板接觸位置的應力集中是使該模型無法得到精確解析解的主要因素,考慮支撐柱直徑為0 的極限情況。此時驗證模型為圓形薄板的軸對稱彎曲,可以由式(6)得到精確的解析解。
驗證模型取半徑15 mm、厚度2 mm 的圓形薄板,對薄板周邊施加固定約束,薄板上表面施加1 MPa 均布荷載,材料為6061 鋁合金。通過Ansys 有限元仿真軟件,求得驗證模型中心位置應力大小為26.86 MPa。相同條件下式(6)求得的解析解為30.23 MPa,仿真誤差為11%,具備一定的仿真精度。
2 實驗結果與討論
對于大面積蒸汽腔結構穩定性問題,主要需要考慮在腔體最大應力位置不發生損壞或斷裂,即保證腔體應力不超過腔體材料的屈服應力。本節將通過有限元仿真探究代表單元中各參數對蒸汽腔體最大應力的影響,并得到腔體最大應力隨各參數變化的函數關系。
已知軸對稱圓形薄板的應力分布與本文代表單元模型應力分布相似,由式(6)可知圓形薄板的最大應力在ρ=0,z=h/2處取得,有
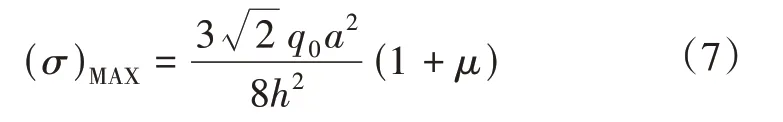
其中,a2=S圓形/π,故有
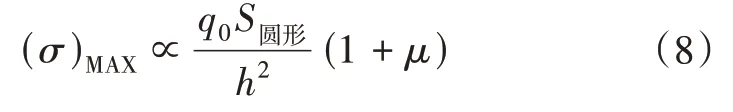
可見當其他條件一定僅改變圓板半徑時,其最大應力正比于薄板的受力面積。代表單元模型最大應力表達式應與式(8)一致,其受力面積為

代入式(8)有
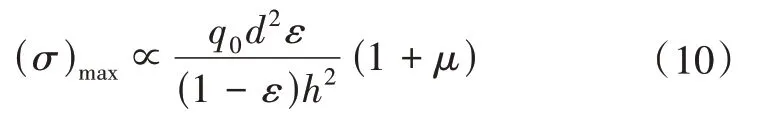
式(10)可表征代表單元中各參數對結構最大應力的影響趨勢,通過下文的仿真數據可以確定各參數與最大應力之間準確的函數關系和具體的系數大小。
2.1 支撐柱直徑對單元體最大應力的影響
如圖2(a)所示,當固定板厚時,相同柱直徑下,孔隙率越大,最大應力越大;相同孔隙率下,結構的最大應力隨著支撐柱直徑的增大而增大;不同孔隙率下,擬合函數中柱直徑前的比例系數不同但指數項相同,都為2.1,說明比例系數與孔隙率有關,指數項與孔隙率無關。如圖2(b)所示,當固定孔隙率時,相同柱直徑下,板厚越大,最大應力越小;相同板厚下,結構的最大應力隨著支撐柱直徑的增大而增大;且不同板厚下,擬合函數中柱直徑的指數項相同,都為2.1,故板厚只影響直徑項前的比例系數,與指數項無關。
由圖2可知,仿真結果中柱直徑對最大應力的影響趨勢與式(10)相一致。代表單元模型中支撐柱直徑對結構最大應力的影響符合如下表達式:
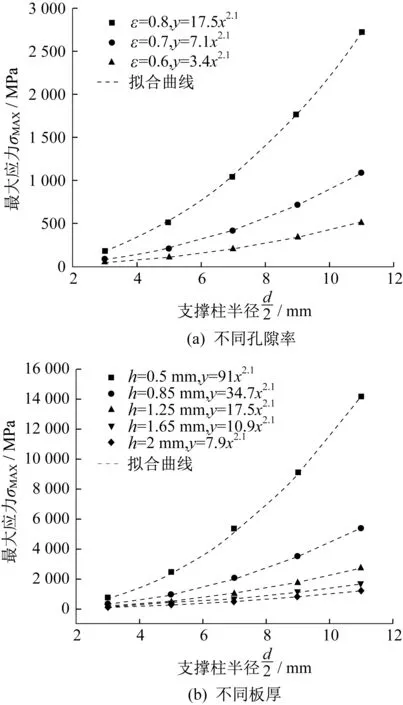
圖2 柱直徑對最大應力的影響Fig.2 Influence of column diameter on the maximum stress
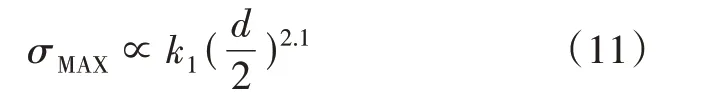
其中,k1為待定系數,包含孔隙率和板厚的影響,而直徑的指數項為固定值2.1,作為式(10)中直徑指數項的修正。
2.2 孔隙率對單元體最大應力的影響
由式(10)可知,孔隙率對最大應力影響的形式應為無量綱ε/(1 -ε),以ε/(1 -ε)為橫坐標,最大應力為縱坐標,在不同支撐柱直徑和板厚條件下得到仿真結果,如圖3所示。
如圖3(a)所示,當固定板厚時,相同孔隙率下,最大應力隨著支撐柱直徑的增大而增大;相同柱直徑下,最大應力隨著孔隙率的增大而增大;不同柱直徑只影響ε/(1 -ε)的比例系數,對其指數項無影響。如圖3(b)所示,當固定柱直徑時,相同孔隙率下,最大應力隨著板厚的增大而減小;相同板厚下,最大應力隨著孔隙率的增大而增大;不同的板厚同樣只影響ε/(1 -ε)的比例系數,指數項與圖3(a)中一致,都為1.534。因此,孔隙率對最大應力的關系式為
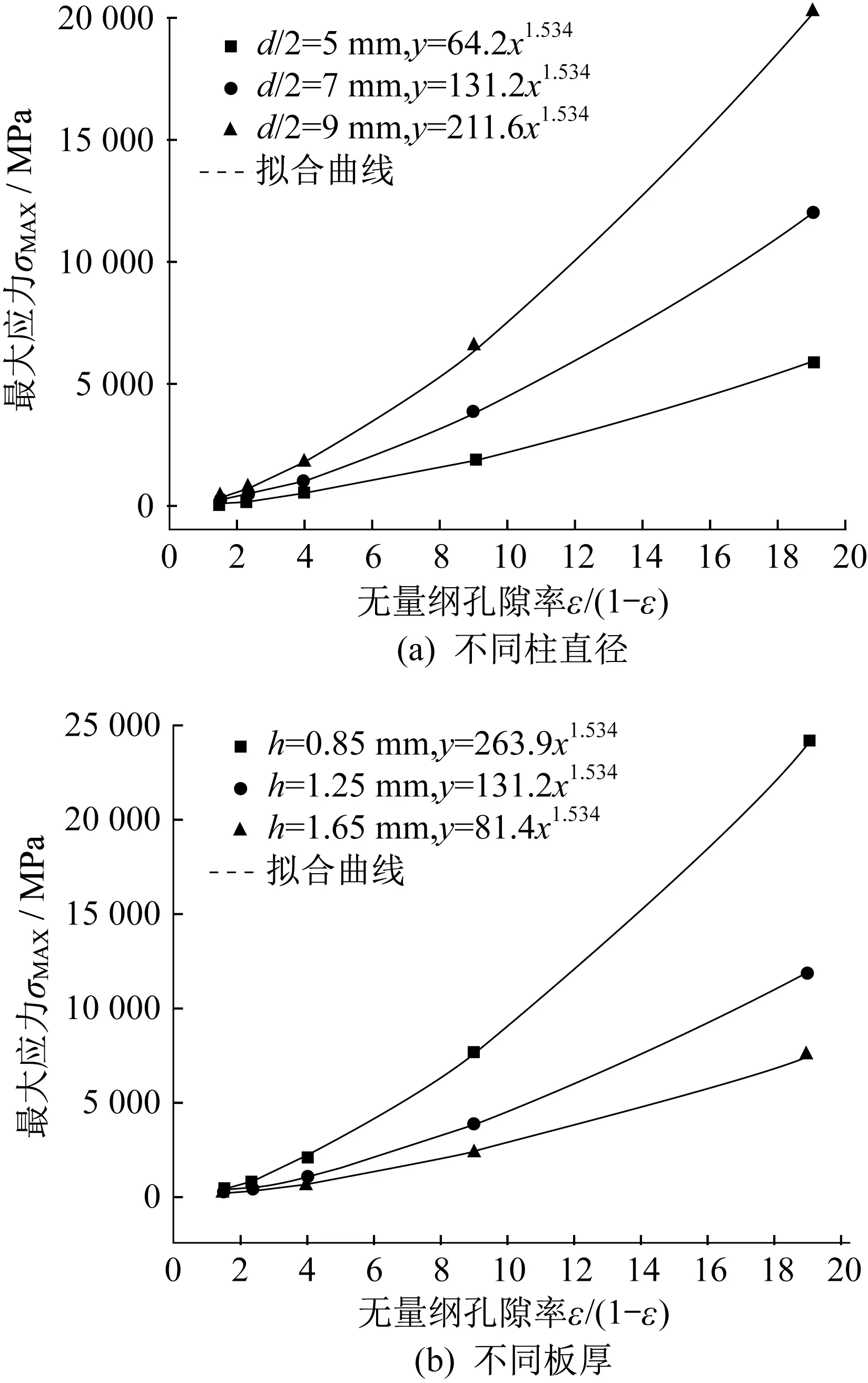
圖3 孔隙率對最大應力的影響Fig.3 Influence of porosity on the maximum stress
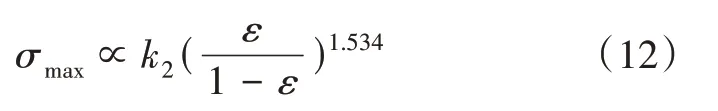
其中,k2受板厚和支撐柱直徑大小的影響,可以發現式(12)中孔隙率對最大應力的影響規律與式(10)相吻合,其中指數項1.534 為式(10)中相應ε/(1 -ε)指數項的修正值。
2.3 板厚對單元體最大應力的影響
如圖4(a)所示,當固定支撐柱直徑時,相同板厚下,最大應力隨著孔隙率的增大而增大;相同孔隙率下,最大應力隨著板厚的增加而減小;不同的孔隙率只影響擬合函數中的比例系數和常數項,對板厚的指數項無影響。由圖4(b)可知,當固定孔隙率時,相同板厚下,最大應力隨著柱直徑的增大而增大;相同支撐柱直徑下,最大應力隨著板厚的增加而減小;不同的柱直徑下板厚的指數項相同。可以發現板厚與最大應力呈負相關,與式(10)相一致,當改變孔隙率和柱直徑時,板厚的指數項皆為-1.94,故板厚與最大應力的函數關系可表示為
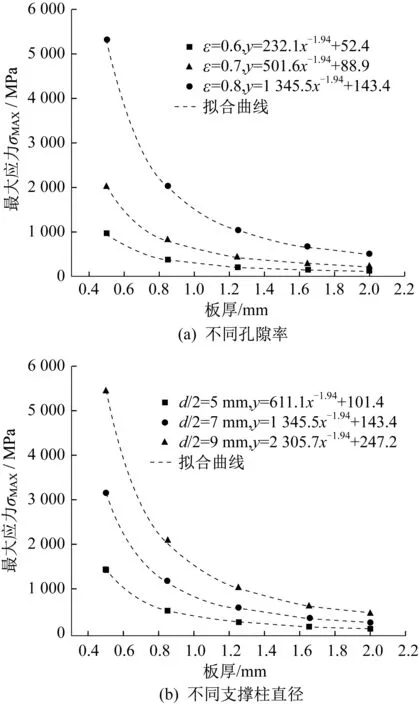
圖4 板厚對最大應力的影響Fig.4 Influence of plate thickness on the maximum stress
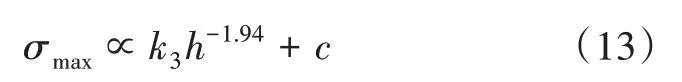
其中,k3、c與孔隙率和支撐柱直徑有關,指數項-1.94為式(10)中板厚指數項的修正值。
2.4 腔體內外壓差對單元體最大應力的影響
由式(10)可知,當單元體結構確定時,腔體內外壓差與單元體的最大應力呈正比例關系,最大應力隨著內外壓差的增大而增大。若某一單元體結構在腔體內外壓差p0=8MPa 時最大應力為σ0,則通過圖5可知,同一結構不同壓力p0下的最大應力σmax為
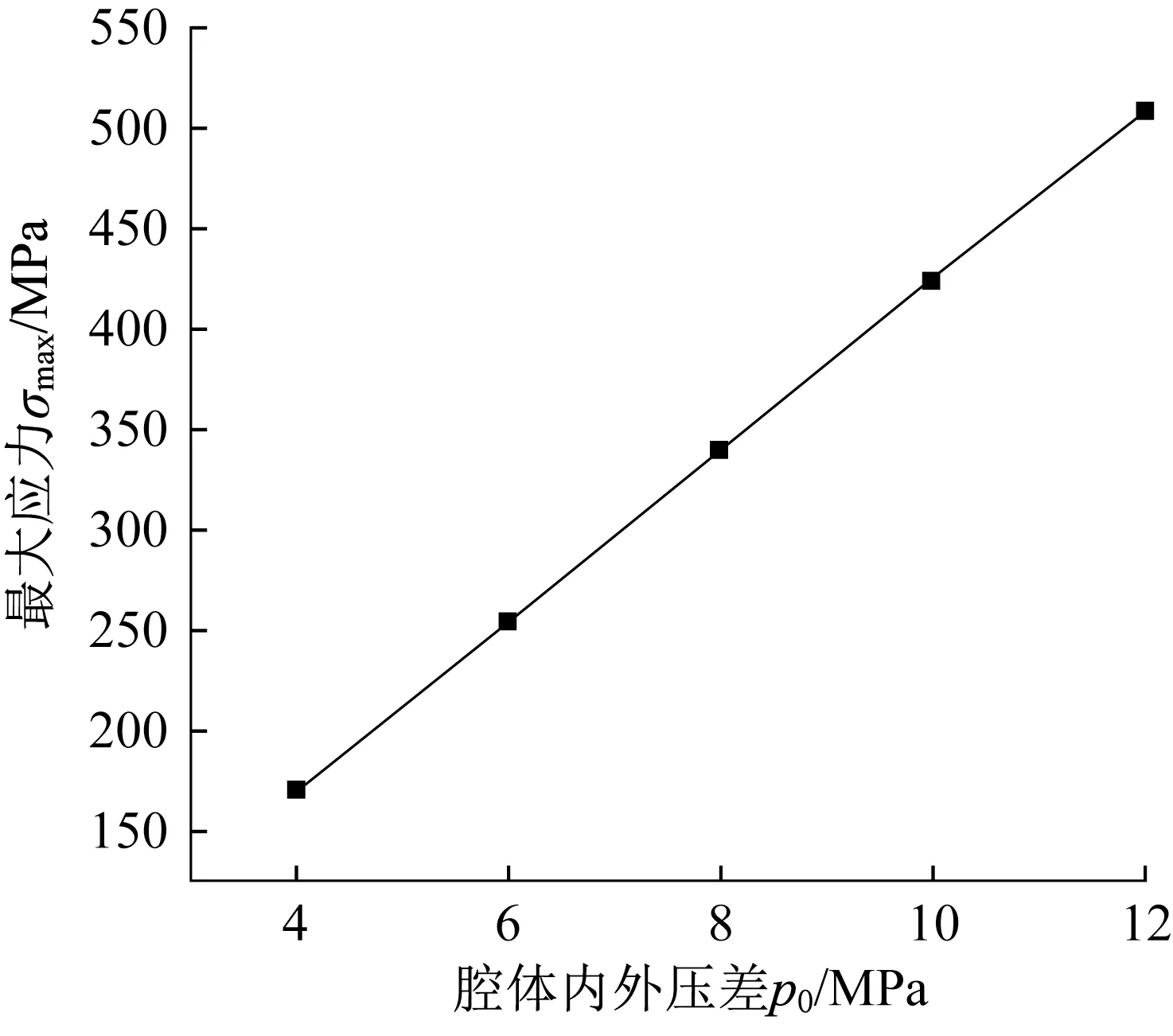
圖5 腔體內外壓差對最大應力的影響Fig.5 Effect of differential pressure on the maximum stress
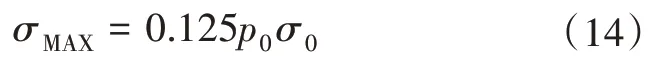
2.5 最大應力關聯式
在上文中,分別討論了代表單元中的3 個結構參數以及腔體內外壓差如何分別影響最大應力,確定了各自與最大應力的函數關系式。采用分離變量的方法,對上述式(11)-(14)進行擬合,可得如下函數擬合結果:
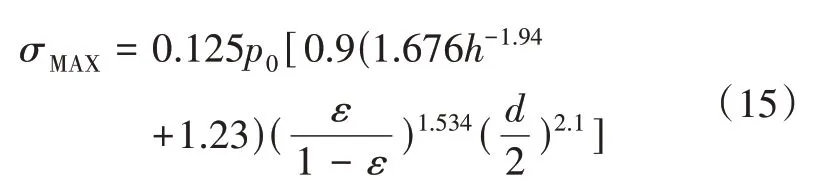
其中,σmax為蒸汽腔最大應力(MPa)、h為蒸汽腔上下板厚(mm)、ε為孔隙率、d為支撐柱直徑(mm)、p0為腔體內外壓差(MPa)。
同時對擬合所產生的誤差進行了預估。對于大多數合金或純金屬,它們的屈服應力都在1000 MPa 以內,故選取了1000 MPa 以內的仿真值,將其與相同參數條件下的擬合函數所求值進行了比較,兩者平均相對誤差為13%,證明擬合函數具備一定的擬合精度。
3 結 論
我國航天技術的發展對大面積超薄蒸汽腔的力學性能提出了更高的要求。本文借助有限元仿真和代表體元法,分別對影響蒸汽腔力學性能的結構參數進行了研究。通過仿真計算,確定了各參數與腔體最大應力的具體函數關系。結果表明,蒸汽腔最大應力受蒸汽腔上下板板厚、孔隙率、支撐柱直徑、腔體內外壓差等因素共同影響。
(1)當孔隙率和板厚一定時,支撐柱直徑與腔體最大應力呈正相關,即最大應力隨著支撐柱直徑的增大而增大,其影響規律近似于二次函數。進一步確定支撐柱直徑的指數項為2.1,比例系數與孔隙率和板厚有關。
(2)當支撐柱直徑和板厚一定時,最大應力隨著孔隙率的增大而增大,且孔隙率以無量綱ε/(1-ε)的形式對最大應力產生影響,無量綱ε/(1-ε)的指數項為1.534,比例系數與支撐柱直徑和板厚有關。
(3)當支撐柱直徑和孔隙率一定時,板厚與腔體最大應力呈負相關,即最大應力隨著板厚的增大而減小,板厚指數項為-1.94,其比例系數與常數項均與支撐柱直徑和孔隙率有關。
(4)當蒸汽腔結構確定時,腔體的最大應力隨蒸汽腔內外壓差增大而增大,兩者呈正比例關系。
(5)在以上結論的基礎上,歸納出了支撐柱直徑、孔隙率、板厚和內外壓差對最大應力共同作用的函數關系式,通過該關系式可以對不同結構參數蒸汽腔的最大應力進行合理預估,對大面積超薄蒸汽腔的設計具有一定參考價值。
由于蒸汽腔在不同應用場景下的復雜熱源條件,本文未將溫度梯度對腔體應力的影響納入考慮,未來需要更加全面地進行熱應力評估,即結合蒸汽腔內工質的相變換熱,求解腔體的溫度場,分析熱應力對腔體力學性能的影響。

