基于線模量波速時間差的10 kV自閉/貫通線路故障測量

劉秦娥，王曉東

（國網(wǎng)湖北省電力有限公司襄陽供電公司，湖北 襄陽 441100）

0 引 言

鐵路10 kV自閉/貫通線，在鐵路電氣系統(tǒng)中具有重要的作用。但因為線路附近常有各種施工現(xiàn)場，復(fù)雜環(huán)境等因素，經(jīng)常造成線路故障，且造成的故障類型多變復(fù)雜，想要定位故障也較為困難[1-3]。

目前，傳統(tǒng)的故障測距方法主要有2種，即阻抗法和行波法。但上述的2種方法在10 kV自閉/貫通線路不再適用。因為該線路的在平常狀態(tài)下是單個電源供電，且由架空線路和電纜線路2種線路混合線路構(gòu)成的。故障點產(chǎn)生的故障行波含有2種分量，一種是線模分量，另一種是零模分量。區(qū)分這2種分量的重要因素之一是這2個行波分量的波速不同[4-7]。因而本文針對該特點將其按照線路段上不同的波阻抗進行分段。由此根據(jù)行波到達同一端的時間差值作為故障測距的關(guān)鍵變量，從而便可以計算出故障距離。

1 混合線路模量波速法故障測距

電纜-架空線混合線路模型如圖1所示，其中M、N為線路2端，將線路平均分成n份，分別為x1,x2,…,xn。

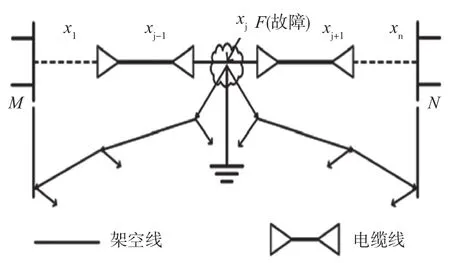
圖1 電纜-架空線混合線路模型

由圖1可知，xjF表示在t0時刻，線路j發(fā)生單相接地短路故障（其中F為發(fā)生故障的位置），則由相關(guān)模分量的計算公式為

式中：t1為線模分量到達端線的時間；t0則為零模分量；第i段線路中線模波速和零模波速分別為相應(yīng)的計算結(jié)果為

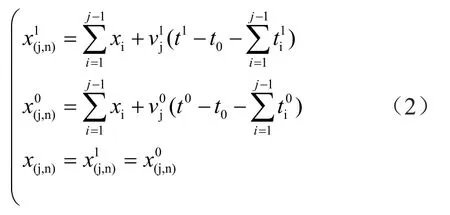
當j=1時，作下述等式變換

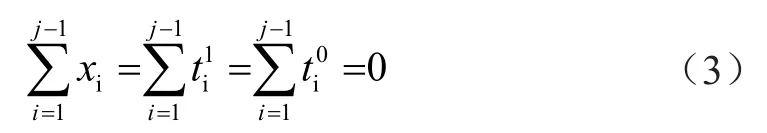
同時，化簡式（2）可得

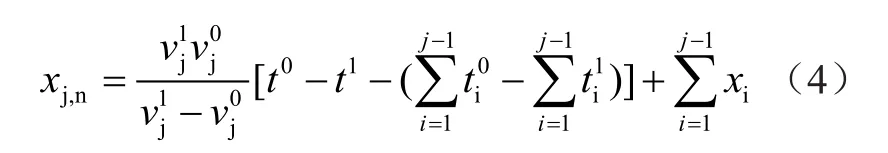
若令

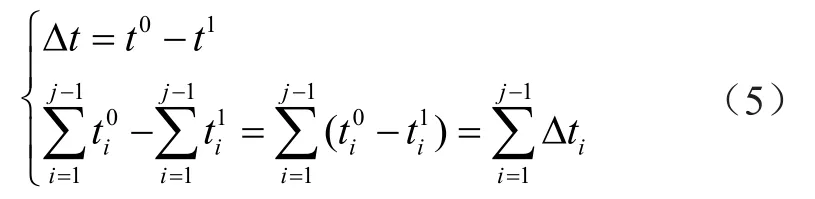
則式（4）則可化簡為

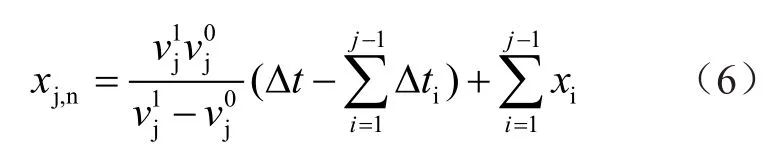
由式（6）可得

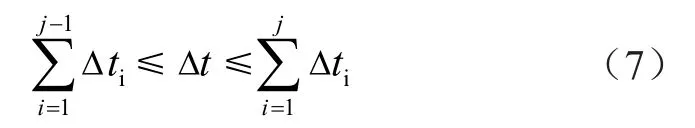
則上式即為故障距離計算的判別式。

2 故障定位的具體實現(xiàn)方法

2.1 模量分量的波形獲取

通過解耦的方法獲得模量分量的波形。如圖2所示為3個橫模分量行波的演示圖。空間模量是前2個分量，其傳播的方法是以輸電線路為1個回路；地中模量則是以大地為分量。

2.2 兩個模分量的波速計算

在分布參數(shù)電路中，通過求解電磁波波動方程即可確定波速，公式為

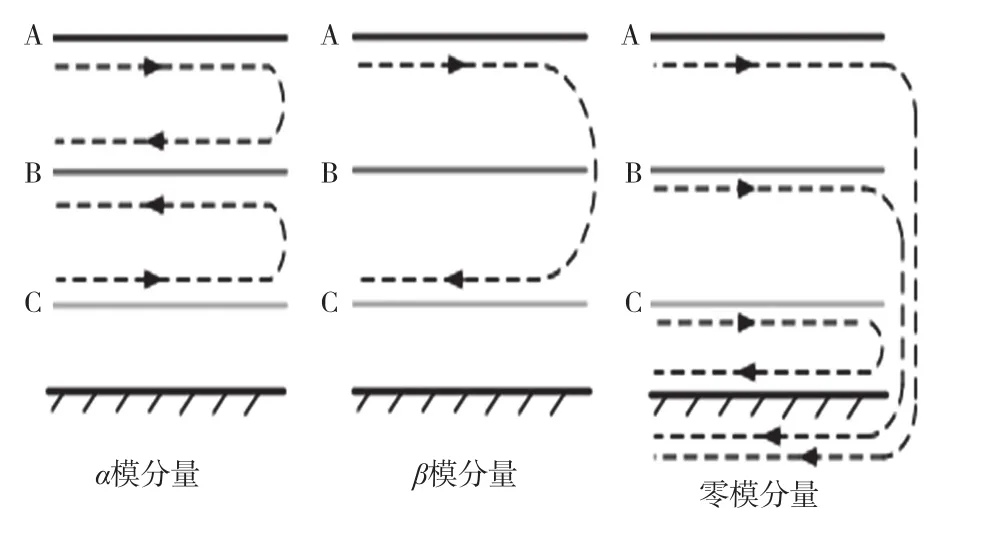
圖2 三相輸電線路的α、β、零模分量

式中：vq為行波波速；w為角頻率；βq為衰減常數(shù)。衰減常數(shù)計算公式為

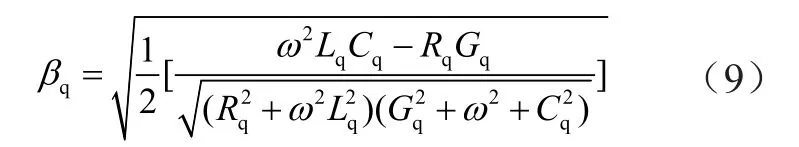
式中：Rq、Lq、Cq和Gq分別為均勻有損輸電線單位長度正序、負序或零序的電阻、電感、電容和電導(dǎo)。

當系統(tǒng)正常運行時的波形是平穩(wěn)的，而一旦發(fā)生故障，則波形會出現(xiàn)突變，出現(xiàn)1個非平穩(wěn)信號，由波形出現(xiàn)的突變點來確定行波的波頭位置[8]。

本文使用小波變換的波形變換算法來識別波形發(fā)生突變，如圖3所示為小波變換時域圖。

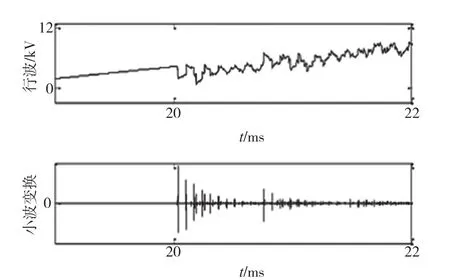
圖3 故障行波及其小波變換時域圖

可以由上述算法快速檢測到波頭。

3 仿真分析

為了驗證本文提出算法的有效性，通過MTLAB的仿真模塊來進行驗證。首先建立1個10 kV自閉/貫通的線路，為了保證架空線路和電纜線路的混合，本文使用電纜和架空線路交替的模型，一共6段混合線路。本文設(shè)線路總長度為60 km,則每段混個線路的長度為10 km。根據(jù)式（6）和判別式（7），得到如圖4所示的曲線。

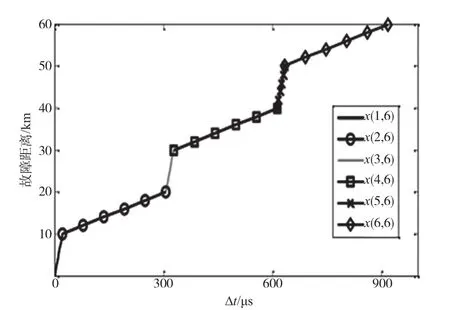
圖4 仿真模型故障距離與模量行波時間差特性曲線

在仿真中，設(shè)置仿真時長為0.04 s,采樣的頻率為2 MHz,則得到的線路首端分量行波如圖5、圖6所示。

圖5 線模故障電壓行波

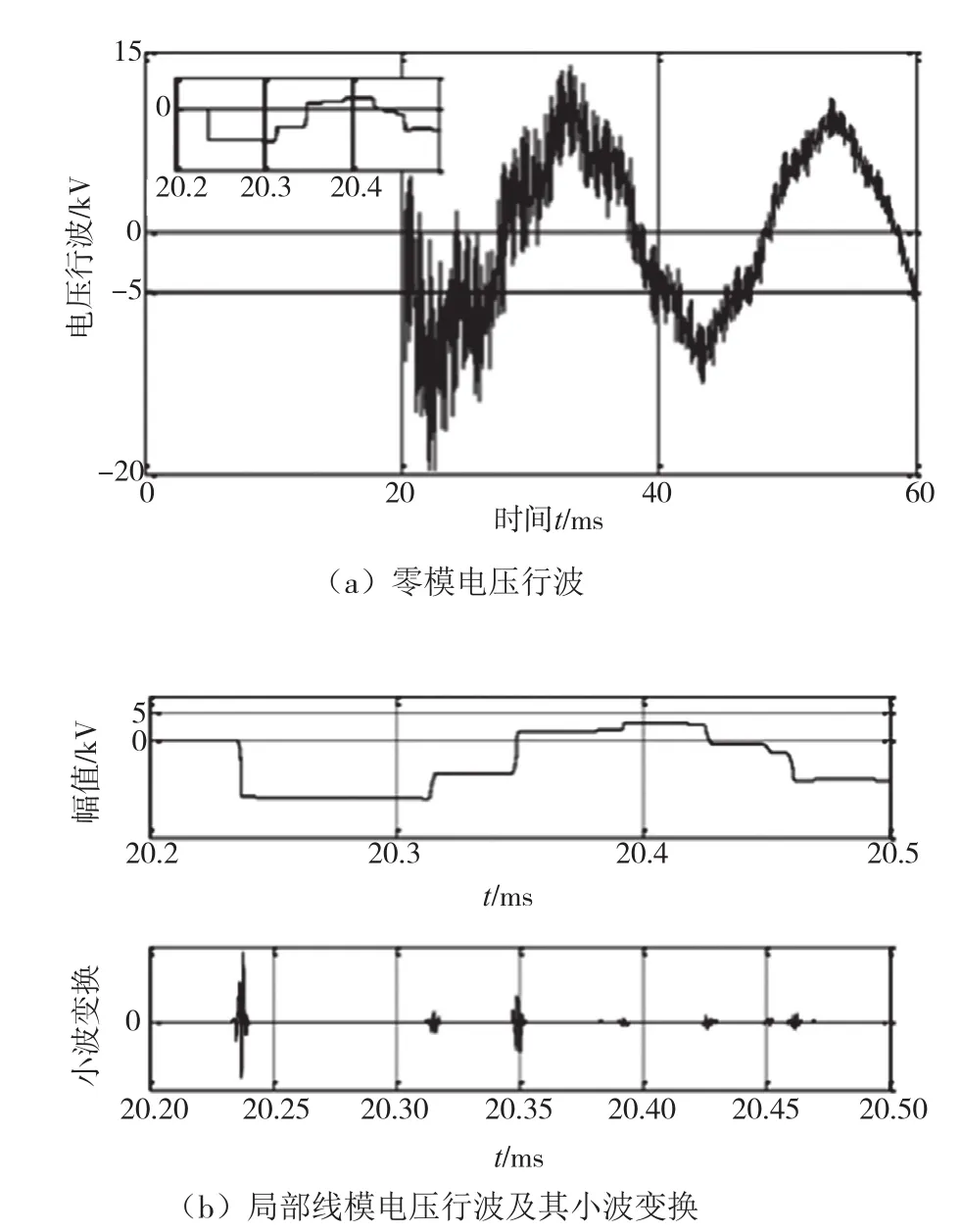
圖6 零模故障電壓行波

則由上述可以計算出故障距離為

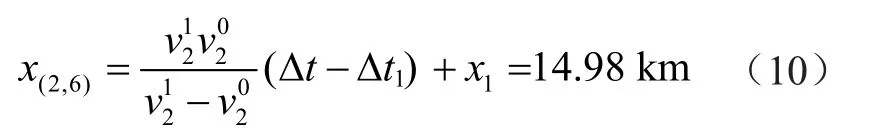
在線路其他的故障位置獲得的情況如表1所示。

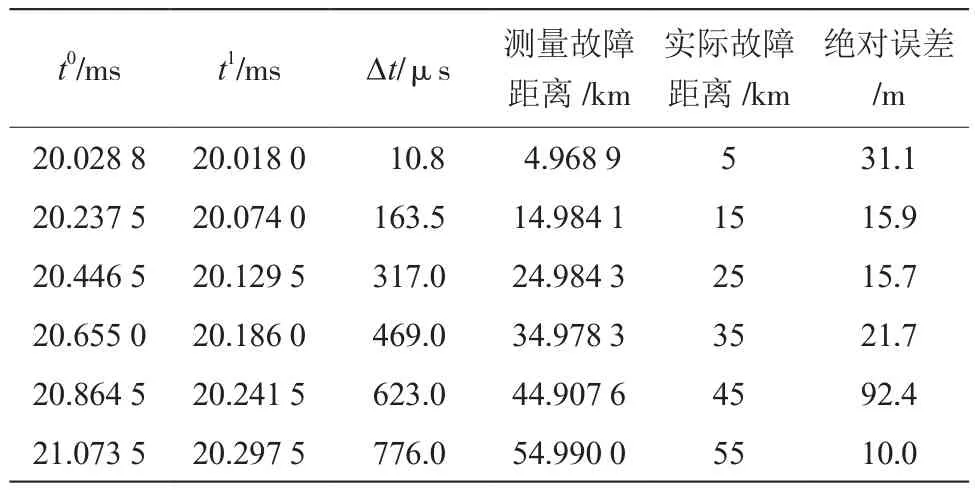
表1 模量行波時間差值法故障測距結(jié)果

上述的結(jié)果表明，本文提及的算法具有較高的魯棒性和精度。

4 結(jié) 論

針對傳統(tǒng)行波算法不適用于多段的混合線路這一現(xiàn)狀，提出一種彌補該缺陷的改進算法。首先，利用2種模量不同的波速來彌補傳統(tǒng)算法中需要精確的時鐘同步的這一缺點。其次，在不同的故障點進行比較，確定算法的魯棒性。最后，利用MATLAB的仿真模塊進行對上述方法的驗證，結(jié)果表明了本文提出的方法的有效性。