機(jī)器人單足系統(tǒng)沙土跳躍剛-散耦合動力學(xué)分析1)

孫昊 劉鑄永 劉錦陽

(上海交通大學(xué)船舶海洋與建筑工程學(xué)院,水動力學(xué)教育部重點實驗室,上海 200240)

引言

機(jī)械系統(tǒng)與散體間的接觸在近年來受到越來越多的關(guān)注,如探索太空時探測器在外星體表面的著陸、仿生機(jī)械在顆粒場上的運(yùn)動等等.以“探月計劃”為例,隨著人類的腳步逐漸踏入太空,未來的太空科學(xué)任務(wù)將大量地涉及在太空飛行或行星探索的過程中收集、存儲和返回某些樣本材料.為了這些樣品的采樣和返回任務(wù)可以順利開展,需要設(shè)計可靠的在沙土上順利完成運(yùn)動并與沙土碰撞的車輛[1-3].有別于傳統(tǒng)履帶式探測車,近年來跳躍式探測車逐漸受到研發(fā)人員的重視[4-7],跳躍式探測車在設(shè)計上有小而輕的優(yōu)點,可以進(jìn)一步控制設(shè)計尺寸,而如何提高其跳躍性能和避障減震能力是其進(jìn)一步發(fā)展的重點之一.這就需要進(jìn)一步研究探測車在跳躍行為中受到來自沙土的耦合阻力,對這種沙土撞擊耦合的動力學(xué)響應(yīng)的理解將為車輛設(shè)計提供更多的魯棒性,并提高整個系統(tǒng)的可靠性.在諸多研究中,機(jī)器人單足系統(tǒng)的簡化模型被應(yīng)用于顆粒介質(zhì)和機(jī)器人的動力學(xué)耦合特性研究實驗中[8].

為了更好地理解散體與機(jī)械的耦合效應(yīng),對散體顆粒物質(zhì)的研究不僅需要實驗的觀測記錄,又需要細(xì)觀機(jī)理的準(zhǔn)確分析.顆粒材料,也稱為散體介質(zhì),是由數(shù)目龐大且相互作用的離散宏觀固體顆粒組成的多相體系,它在自然界中以人們一般認(rèn)識的沙土為主,是除了流體以外最廣泛存在的一種物質(zhì)形式.目前對散體研究取得的進(jìn)展包括耗散顆粒氣體、離散元理論、顆粒團(tuán)混合與分級、振動機(jī)理等方面[9-10].與傳統(tǒng)連續(xù)介質(zhì)的模型不同,散體顆粒雖排列緊密,但顆粒呈現(xiàn)的卻是以接觸力鏈彼此連接形成的空間網(wǎng)絡(luò).散體動力學(xué)具有如下特殊性質(zhì)[11-12]:(1)只有剪應(yīng)力達(dá)到一定閾值,顆粒才會產(chǎn)生流動,這區(qū)別于流體剪應(yīng)力與流速梯度相關(guān)的情況,表明了散體與流體的一定差異[13-14];(2)散體材料的屈服應(yīng)力常常與流動變形的時間歷程相關(guān),并且當(dāng)散體應(yīng)變率發(fā)生改變時,屈服應(yīng)力也會相應(yīng)改變;(3)散體間的摩擦力會令散體顆粒產(chǎn)生顯著的剪漲效應(yīng);(4)顆粒在流動時,它的黏性系數(shù)不是保持恒定,而是與邊界層剪切率緊密相關(guān)的函數(shù).如何表征顆粒材料的力學(xué)性能不但是力學(xué)學(xué)科重要的前沿基礎(chǔ)科學(xué)問題,而且有著重要的工程應(yīng)用前景.

為了將復(fù)雜的散體理論與快速發(fā)展的計算技術(shù)適配,誕生了將傳統(tǒng)的連續(xù)型土壤化為一定形狀的顆粒集群進(jìn)行計算的離散元(discrete element method,DEM)仿真技術(shù).目前在對大規(guī)模的顆粒場進(jìn)行快速接觸檢測、將復(fù)雜的散體理論等效為利于計算的接觸模型、引入顆粒間范德華力、高溫場、非球狀顆粒、柔性顆粒等更多樣的微觀模型[15-20]等方面,都不斷取得突破.采用DEM 進(jìn)行仿真,首先需要對顆粒場物性參數(shù)進(jìn)行標(biāo)定,這就需要對工況進(jìn)行一定的預(yù)判斷,選擇合適的散體顆粒接觸模型.完成了顆粒場的建模后,在對剛散耦合的動力學(xué)研究中,需要基于實物實驗和仿真分析進(jìn)一步得到適合快速計算的簡化力學(xué)模型,來表征物體在侵入顆粒場時的阻力效應(yīng),對此國內(nèi)外有非常多的研究,包括顆粒場的阻力形式研究[21]、基于準(zhǔn)靜態(tài)侵入沙土研究阻力的類流體靜壓效果[22-25]、基于傳統(tǒng)土力學(xué)連續(xù)土體破壞分層受力分析[26-28].其中基于Poncelet 公式的拓展研究猶為豐富[29-33],這依賴于Poncelet 公式簡潔的形式和較好地反映真實動力學(xué)效應(yīng).

本文采用離散元法模擬顆粒場,以及采用多體動力學(xué)方法對機(jī)械系統(tǒng)進(jìn)行建模,對機(jī)器人單足系統(tǒng)在顆粒場跳躍問題進(jìn)行耦合動力學(xué)仿真,分析了接觸面積、機(jī)器人足底形狀等不同足部設(shè)計對于機(jī)構(gòu)受到顆粒場侵入阻力的影響.研究發(fā)現(xiàn)Poncelet定理在描述動態(tài)的足部下壓顆粒場的過程中能大致地符合阻力變化,但仍存在一定的誤差,尤其是在下壓深度較大處存在收斂性較差的問題.因此基于經(jīng)典土力學(xué)Prandtl-Reissne 理論,從顆粒場受壓分層的形式和動量傳遞出發(fā),對動阻力項進(jìn)行修正,提出了修正的Poncelet 公式.通過與剛-散耦合動力學(xué)仿真結(jié)果比較,說明所提出的修正公式能更準(zhǔn)確地計算機(jī)械系統(tǒng)在顆粒場上的動力學(xué)響應(yīng),尤其在達(dá)到一定侵入深度后,相較于原始Poncelet 公式,修正公式計算的侵入阻力體現(xiàn)出和仿真結(jié)果一致的收斂性.本研究將為新型探測器在行星土壤上運(yùn)動的系統(tǒng)設(shè)計提供動力學(xué)建模理論和技術(shù)支撐.

1 跳躍模型與剛散耦合理論

1.1 單足系統(tǒng)的跳躍建模

為了探索離散元仿真技術(shù)在定量研究機(jī)械系統(tǒng)與散體的動力學(xué)耦合效應(yīng)中如何發(fā)揮作用,設(shè)計了一個彈簧單足機(jī)構(gòu)研究其顆粒場上的一維跳躍運(yùn)動[34].在過往的研究中往往基于傳統(tǒng)土力學(xué)轉(zhuǎn)靜態(tài)侵入沙土[26]、或是純粹的實物實驗設(shè)計分析[34].而從離散元仿真角度對于這種機(jī)器人單足系統(tǒng)與沙土環(huán)境的耦合效應(yīng)進(jìn)行動力學(xué)仿真值得進(jìn)一步探索.

由于機(jī)械足與顆粒場的動力學(xué)耦合效應(yīng)體現(xiàn)在機(jī)械腿足部對顆粒場的侵入阻力,所以在仿真上忽略除足部外其余結(jié)構(gòu)的設(shè)計,選擇將模型簡化為“機(jī)械腿桿身-驅(qū)動電機(jī)-彈簧阻尼器-機(jī)械腿足部”的單足系統(tǒng),如圖1(a)所示.為了使單足系統(tǒng)能在顆粒場上較好地完成跳躍動作,經(jīng)過測試后設(shè)計了驅(qū)動電機(jī)在機(jī)械腿桿身上進(jìn)行位移驅(qū)動,當(dāng)單足系統(tǒng)在顆粒場上靜止穩(wěn)定后,令電機(jī)快速沿桿身向上運(yùn)動,從而令桿身向下壓縮彈簧阻尼器,積蓄跳躍所需的彈性勢能,這時機(jī)械腿足部受到彈簧的向下壓力,對在靜止穩(wěn)定的狀態(tài)下進(jìn)一步侵入顆粒場,受到來自顆粒場的侵入阻力.當(dāng)彈簧基本達(dá)到最大壓縮量、且由于自身剛度效應(yīng)開始反彈時,電機(jī)開始沿機(jī)械腿桿身向下運(yùn)動,使得桿身在大地基上向上運(yùn)動,并使得彈簧阻尼器充分釋放,從而令單足系統(tǒng)高高跳起,從而完成整個跳躍動作.為了提升電機(jī)的驅(qū)動效果,設(shè)計電機(jī)為鐵質(zhì),而機(jī)械腿足部和桿身設(shè)計為鋁制.單次跳躍中機(jī)械腿桿身、電機(jī)、機(jī)械腿足部在豎直方向的位移如圖1(b)所示.

圖1 單足機(jī)器人系統(tǒng)建模[34]Fig.1 Single-leg robot system modeling[34]

1.2 散體接觸模型

離散元方法的出現(xiàn)使得可以在更小的尺度應(yīng)用顆粒間接觸的力學(xué)理論.顆粒的接觸理論可以大致根據(jù)干濕性分為有黏與無黏兩種[35].無黏顆粒的計算理論相對簡單,適合快速計算.而在實際表征沙土顆粒的性質(zhì)時,為了更好地還原顆粒場受到劇烈沖擊后的破壞情況,也往往需要考慮顆粒間由于表面材質(zhì)或者小分子范德華力帶來的黏性作用.

如圖2 所示,本文采用Hertz-Mindlin(no slip)接觸模型和Hertz-Mindlin with JKR Cohesion 接觸模型來分別針對無黏接觸和有黏接觸,后者在前者的基礎(chǔ)上加入表面凝聚力來反映顆粒間的范德華力[35].

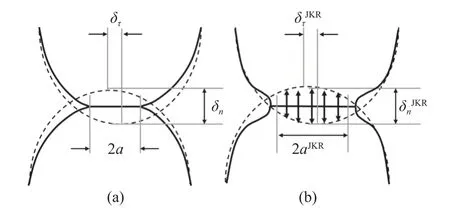
圖2 顆粒間接觸形式:(a)無黏接觸,顆粒接觸區(qū)域受擠壓變形;(b)有黏接觸,顆粒接觸區(qū)域受擠壓表面粘連Fig.2 The contact forms between particles.(a) Non viscous contact:the particle contact area is extruded;(b) viscous contact:the particle contact area is adhered by the extruded surface

Hertz-Mindlin(no slip)接觸模型用于高效計算干沙類顆粒材料.顆粒間的接觸力分為法向彈性力、切向彈性力、法向阻尼力、切向阻尼力,表達(dá)式如下[35]

Hertz-Mindlin with JKR Cohesion 接觸模型在Hertz-Mindlin(no slip)理論上引入了帶表面能量密度的修正,適用于有濕度的泥土顆粒.由于接觸面在黏性效應(yīng)下發(fā)生變化(見圖2(b)),法向相應(yīng)的修改如下[35].

顆粒間引入黏能Δγ,有

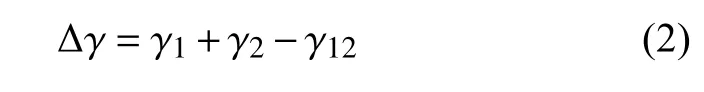
其中,γ1和γ2分別為兩顆粒的表面自由能,γ12為界面能.

顆粒受到的外部載荷為Fn,則由于黏性接觸導(dǎo)致的接觸面半徑a的修改形式為

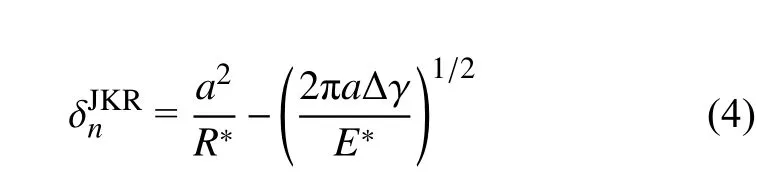
基于新的法向重疊量更新了法向外載荷Fn后,表面黏性力導(dǎo)致的等效法向載荷Fn,JKR為

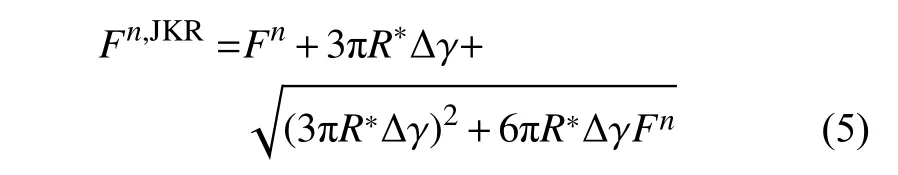
由于黏性效應(yīng),兩顆粒在分開時,促使顆粒表面分開的最大分離力的計算公式為

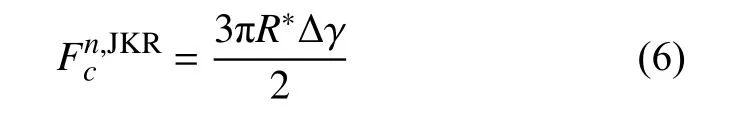
有黏接觸的兩顆粒間切向力的修正同樣類比于法向力修正,在此不再贅述.

1.3 剛-散耦合動力學(xué)方程

對于散體與剛體組成的耦合系統(tǒng),除了剛體系統(tǒng)自身可能存在的彈簧力、阻尼力外,還有散體系統(tǒng)帶來的外力和外力矩,以及其他外載荷.在離散元計算中,通過接觸理論計算得到散體和剛體之間的作用力,加入各自所受的合力與合力矩中,再同時更新剛體和散體的速度和加速度信息,而后更新位置并進(jìn)行下一步迭代.在DEM 計算大尺度物體與大數(shù)量級散體顆粒間的接觸作用力時,為了提高計算效率,會將復(fù)雜的顆粒間接觸模型簡化為彈簧阻尼系統(tǒng),將顆粒間法向和切向的重疊量作為表征彈簧力的壓縮量,將接觸理論歸并到切向與法向的剛度系數(shù)和阻尼系數(shù)的計算中去.

根據(jù)牛頓-歐拉方程,對于單個顆粒,有

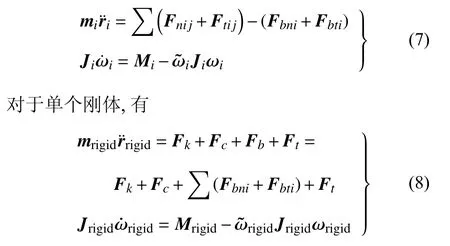
其中,下標(biāo)i和j為發(fā)生接觸的顆粒編號,下標(biāo)rigid 表示與顆粒接觸的剛體.Fnij和Ftij為顆粒間接觸的法向和切向作用力.Fbni和Fbti為顆粒對剛體的法向和切向作用力,Fk為剛體所受彈性力,Fc為剛體所受阻尼力,Ft為剛體所受其余外界約束力和載荷,m和J為質(zhì)量陣和轉(zhuǎn)動慣量陣,r和ω為位置坐標(biāo)陣和角速度陣,Mi和Mrigid分別為單個顆粒和剛體所受的包含接觸力在內(nèi)的所有外力產(chǎn)生的力矩矩陣.

對于本文所研究的機(jī)器人單足系統(tǒng)一維跳動剛-散耦合系統(tǒng),基于速度變分原理,單足系統(tǒng)動力學(xué)方程為

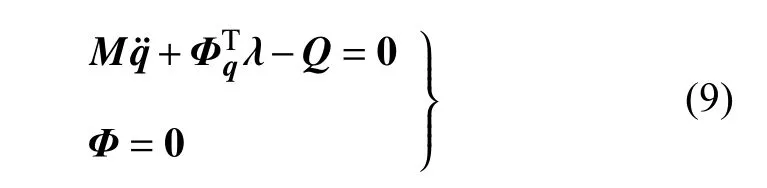
其中,q和為單足系統(tǒng)在一維豎直方向上的位移和加速度陣; Φ為約束力陣,主要項為單足系統(tǒng)桿身和電機(jī)之間的位移驅(qū)動約束; λ為拉格朗日乘子陣;質(zhì)量陣M和外力陣Q具體如下

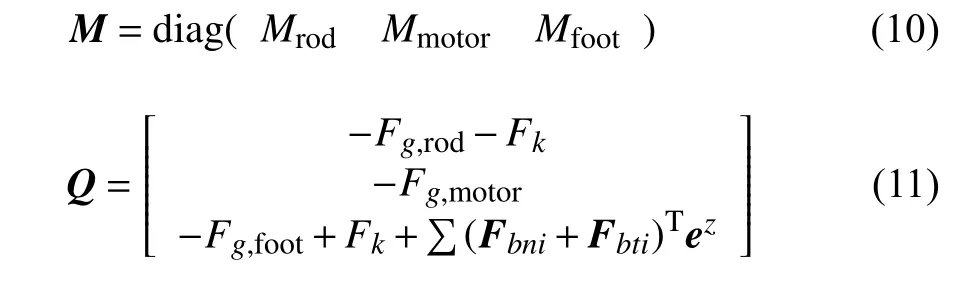
其中,下標(biāo) r od,m otor,f oot 分別代表桿身、電機(jī)、足部;Fg為重力項;Fk為桿身和足部之間的彈簧力元項;為了簡化為豎直方向一維運(yùn)動,僅考慮顆粒對足部的侵入阻力Fbni和Fbti的豎直方向分量.

2 Poncelet 公式修正

1.3 節(jié)完整的剛-散動力學(xué)模型往往運(yùn)用于有限元或離散元的仿真過程中,而在一些追求更高效快捷的情況下,往往需要一個簡潔而統(tǒng)一的定律來反映物體侵入沙土介質(zhì)中所受的阻力,為此,Poncelet等給出了如下表達(dá)式[23]

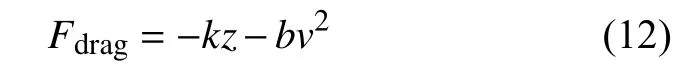
其中,z是物體相對于顆粒場表面的侵入深度,v是物體的速度,k和b被認(rèn)為是僅僅取決于產(chǎn)生接觸的顆粒介質(zhì)和侵入物體的物性參數(shù)的常數(shù).由此,便可以將物體所受的顆粒場阻力Fdrag分解為一個侵入深度相關(guān)的類庫侖摩擦項(Fdrag,st=-kz)和一個侵入速度相關(guān)的類慣性力項(Fdrag,dy=-bv2),這同樣可以類比于流體受力分析[15],有著較好的物理解釋.

本文選擇橫截面直徑20mm、高6 mm 的足底作為測試工況進(jìn)行分析,根據(jù)Poncelet 公式可以得到顆粒場阻力與侵入深度、足部速度的關(guān)系系數(shù).可以看出,在起跳下壓顆粒場時,足部受到彈簧阻尼器的脈沖力和顆粒場逐漸增大的侵入阻力產(chǎn)生了一個先加速后減速的變化.若采用Poncelet 公式進(jìn)行計算,對侵入過程能基本吻合,但在初始加速階段和減速結(jié)束階段,存在較大偏差.

結(jié)合離散元仿真顆粒場受壓分層的演化,并根據(jù)經(jīng)典土力學(xué)Prandtl-Reissne 理論,受壓土體可分層為足底固結(jié)區(qū)域、過渡區(qū)域、被動區(qū)域(見圖3),其中足底固結(jié)區(qū)域與足底保持相同的速度向下共同運(yùn)動.可以認(rèn)為用Poncelet 公式產(chǎn)生的偏差是由于以足部底端的固結(jié)區(qū)域顆粒為主的顆粒場分層演化導(dǎo)致的,這部分顆粒的體積隨著足部下壓而逐漸生長直到成型,從而對顆粒阻力的動阻力項Fdrag,dy=-bv2帶來了影響.

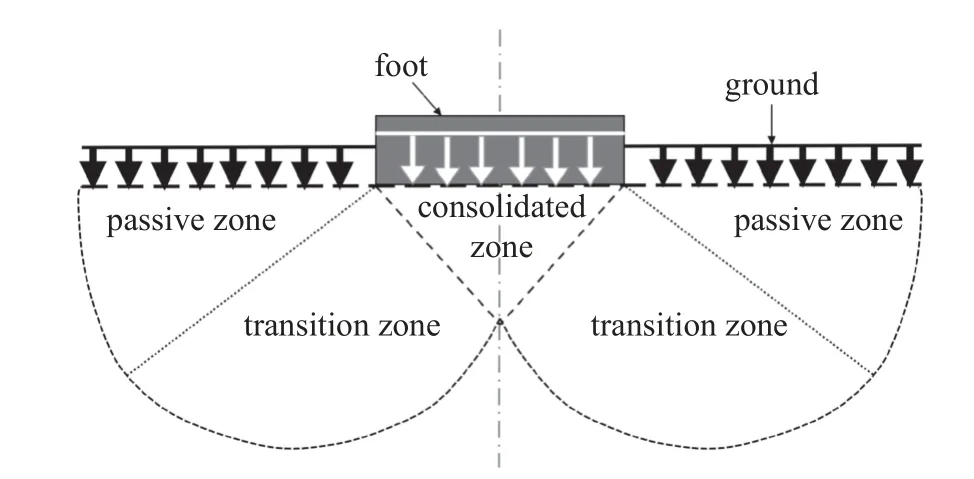
圖3 Prandtl-Reissner 理論足底下壓顆粒場時顆粒場分層示意圖Fig.3 Schematic diagram of soil stratification under pressure of downforce process based on Prandtl-Reissner theory

為了更精準(zhǔn)地描述動阻力項的變化,需要對動阻力項進(jìn)行進(jìn)一步修正:由于顆粒場受擠壓而發(fā)生運(yùn)動,對足部產(chǎn)生了上述動阻力,即(下標(biāo)gra表示沙土顆粒,mgra表示單個顆粒質(zhì)量);而顆粒運(yùn)動產(chǎn)生分層后,動量集中在足底固結(jié)區(qū)域以及周圍過渡區(qū)域的顆粒上,其中足底固結(jié)區(qū)域與機(jī)械腿足部速度基本一致,可直接用足部的運(yùn)動信息去近似描述.故而顆粒場的動量可以用足底固結(jié)區(qū)域顆粒場動量乘以一個近似系數(shù)去描述,即

式中,Mgra,CZ表示足底固結(jié)區(qū)域的顆粒質(zhì)量之和;k1為產(chǎn)生運(yùn)動的整體顆粒場動量與足底固結(jié)區(qū)域顆粒場動量的比例系數(shù),afoot為機(jī)械腿足部的加速度.

下壓過程中足底固結(jié)區(qū)域逐漸生長,假設(shè)固結(jié)區(qū)域的體積與下壓深度在跳躍這一行為下呈正比,則有Mgra,CZ=k2z,因此進(jìn)一步可得

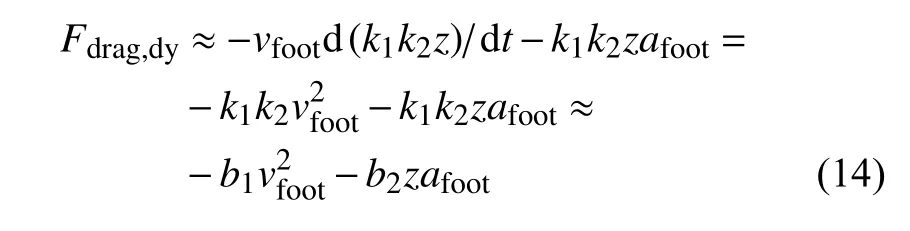
從而將顆粒場的運(yùn)動與足底的運(yùn)動建立近似的線性關(guān)系,用足底運(yùn)動的相關(guān)物理量來表征顆粒場動量損失.這里區(qū)分b1和b2的目的是考慮到顆粒場質(zhì)量等效帶來的偏差,需要增加一個系數(shù)自由度去更好地貼合真實侵入阻力,可以大致認(rèn)為b1=b2.式中的項就是Poncelet 公式中的動阻力項,而b2hafoot項就是增加的動阻力修正項.因此修正后的Poncelet公式完整表達(dá)式為

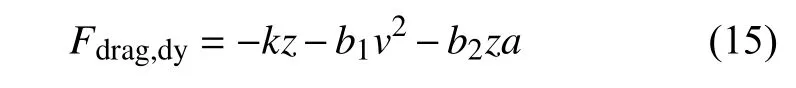
利用修正的Poncelet 公式對測試工況的動力學(xué)響應(yīng)進(jìn)行計算(見圖4 紅線所示修正PonceletFdrag),可以發(fā)現(xiàn)修正后的侵入阻力與各力學(xué)指標(biāo)的關(guān)系都與離散元仿真結(jié)果幾乎完全吻合,從而驗證了所提出Poncelet 修正公式的有效性.且系數(shù)b1=9.07 kg/m,b2=9.49 kg/m,有b1≈b2.直接測試b1和b2相等下的動力學(xué)響應(yīng)效果(見圖5(a)),基本與修正Poncelet 公式及離散元仿真結(jié)果一致,有b1=b2=9.35 kg/m,驗證了修正公式推導(dǎo)的可靠性.通過對多個工況仿真計算結(jié)果,說明今后可近似使用b1=b2來簡化模型.

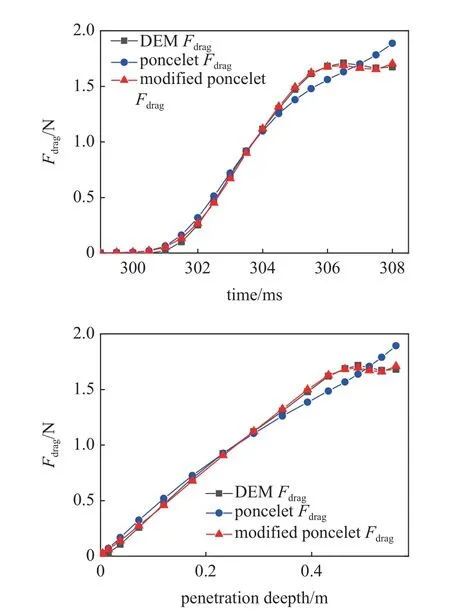
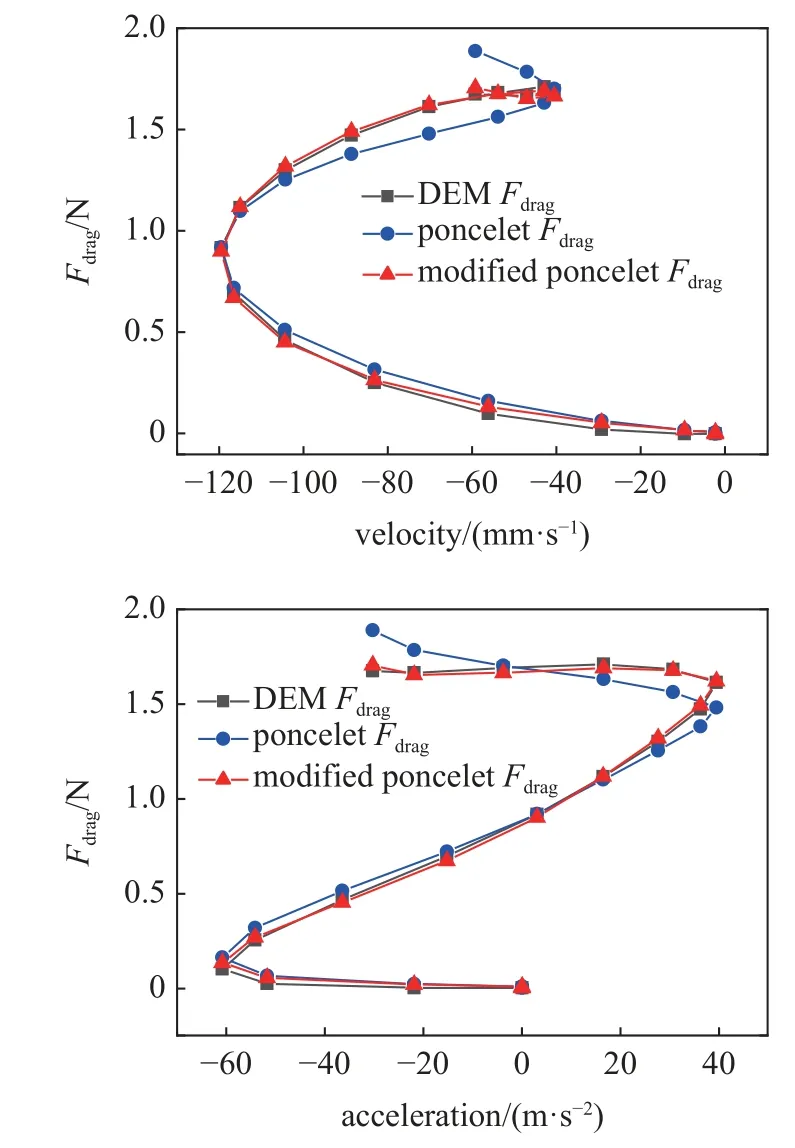
圖4 Poncelet 公式修正前后沙土阻力對比Fig.4 Comparison of dynamic response using modified Poncelet formula or not

對比不同工況下修正后Poncelet 公式計算侵入阻力的結(jié)果,對系數(shù)k,b1,b2進(jìn)行初步分析,發(fā)現(xiàn)不同工況下的b1和b2會在同一個數(shù)量級下產(chǎn)生一定浮動,對足部尺寸和質(zhì)量具有依賴性;而k在不同體積的足部工況下則基本不變,而在不同足底橫截面積下大致呈線性關(guān)系(見圖5(b)).這表明對于相同形狀的機(jī)械腿足部和相同顆粒場,具有近似相同侵入阻力的靜阻力項系數(shù)k.對于不同橫截面積的足部,存在關(guān)系

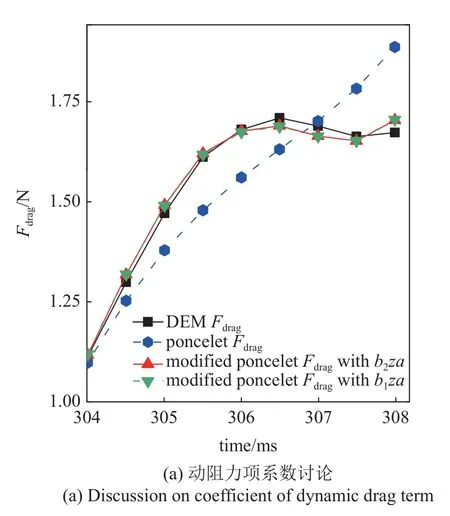
圖5 修正Poncelet 公式參數(shù)分析Fig.5 Parameter analysis of modified Poncelet

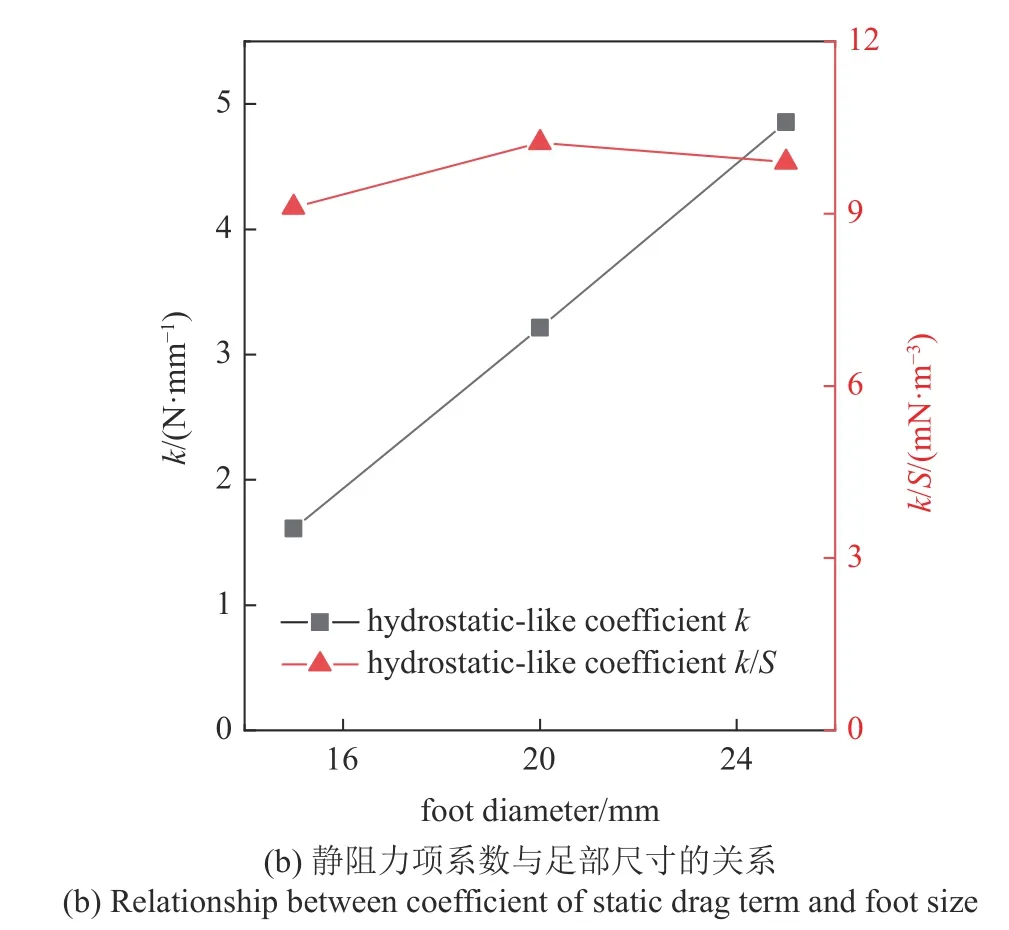
圖5 修正Poncelet 公式參數(shù)分析(續(xù))Fig.5 Parameter analysis of modified Poncelet(continued)

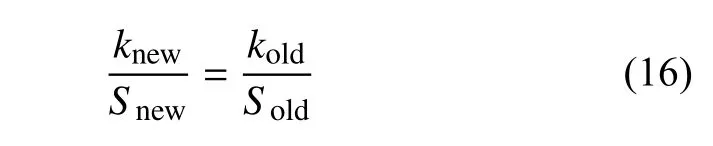
若在低速運(yùn)動下忽略動阻力項而直接使用靜阻力項進(jìn)行計算時,這一系數(shù)轉(zhuǎn)換關(guān)系將帶來很大的方便.

3 足部設(shè)計的動力學(xué)分析

機(jī)械腿足部在彈簧壓縮階段,會同時受到彈簧阻尼器的壓力和顆粒場侵入阻力,由于彈簧阻尼器的力更多依賴于機(jī)械系統(tǒng)激勵力(即電機(jī)驅(qū)動機(jī)械腿桿身運(yùn)動后對彈簧的壓縮)、且足部在顆粒場上的位移變化為小量.故在壓縮階段,彈簧壓力呈現(xiàn)出一種較為均勻的單波峰簡諧力形式.而機(jī)械腿足部在壓縮階段侵入沙土?xí)r,由于自身相當(dāng)于受到可變性顆粒場不完整約束的彈簧振子,故而速度特性呈現(xiàn)出一種振動效應(yīng),這種振動效應(yīng)也對應(yīng)地使得顆粒場的侵入阻力出現(xiàn)波動.而顆粒場隨著足部運(yùn)動的受壓縮變形,可以分為四個階段:(1)足部剛開始壓縮沙土,固結(jié)區(qū)開始出現(xiàn)(固結(jié)區(qū)即經(jīng)典土力學(xué)分析中沙土受到破壞后,固連在足部底端、與足部具有相同速度的顆粒場區(qū)域);(2)足部壓縮速度最大處,固結(jié)區(qū)基本生長成型,固結(jié)區(qū)附近的過渡區(qū)(即顆粒運(yùn)動速度介于足底固結(jié)區(qū)和周圍靜止區(qū)域間的顆粒場區(qū)域)可以明顯地看到;(3)彈簧提前開始釋放,沙土逐漸密實,足部下壓速度開始下降;(4)電機(jī)結(jié)束下壓驅(qū)動,沙土不再進(jìn)一步變形,單足系統(tǒng)機(jī)械腿足部開始起跳,與顆粒場分開.

下面進(jìn)一步分析顆粒場對單足系統(tǒng)的侵入阻力對于足部設(shè)計的依賴性,以及由此帶來的跳躍效果的差異.首先,分析足部與顆粒場的接觸面積的影響,為此設(shè)計了相同質(zhì)量、不同橫截面積的一系列圓柱形機(jī)械腿足部,直徑分布從10mm 至25 mm,接觸面積變化幅度約為600%.若是在硬地面上,由于彈簧阻尼器兩端的桿身和足部質(zhì)量均無變化,在相同驅(qū)動下,跳躍高度基本不受足部形狀的影響.而在可變性顆粒場上,跳躍高度與足部尺寸呈現(xiàn)出對數(shù)型依賴關(guān)系(見圖6(a)),當(dāng)足部直徑為30mm 時,跳躍高度為30.9 mm,足部直徑為25 mm 時,跳躍高度為45.4 mm,變化幅度約為50%,跳躍效果受到了極大的影響.從顆粒場變形的角度來分析機(jī)理,當(dāng)足部的橫截面積增大時,足底沙土固結(jié)區(qū)域的體積也隨之增大,需要足部施加更多的動量來進(jìn)一步壓縮沙土,從而使沙土呈現(xiàn)出一種更緊實、更“剛性”的動力學(xué)效果,表現(xiàn)為沙土達(dá)到最大壓縮效果的用時更短(見圖6(b)),且沙土下壓深度減小(見圖6(c)),并且可以注意到足部下壓顆粒場的深度與接觸面積呈現(xiàn)出良好的反比例關(guān)系,即下壓深度與橫截面積成反比h∝1/S.

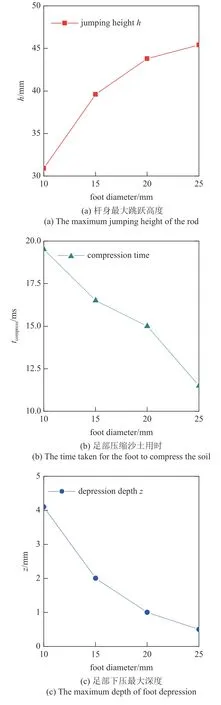
圖6 足部直徑與各動力學(xué)響應(yīng)指標(biāo)的關(guān)系Fig.6 The relationship between the foot diameter and each dynamic response

為了分析足部的質(zhì)量效應(yīng)在跳躍過程中的影響,設(shè)計一系列相同橫截面積不同高度的同材質(zhì)圓柱形足部(直徑20mm,高度為5～ 10mm 分布).在壓縮沙土階段,選擇足部速度最大的時刻展示,此時足部下壓速度約為0.1 m/s,觀察此時顆粒場的縱向速度分布(圖7(a)),可以明顯看出,足底與機(jī)械腿足部速度基本相同的紅色固結(jié)區(qū)域大致呈現(xiàn)圓錐形,且錐角約為45°,在不同質(zhì)量的足部下基本保持一致,且綠色過渡區(qū)域的變化梯度基本一致,由此可以認(rèn)為在相同橫截面積的平面足部壓縮下,沙土的受力分層更多與本身物理性質(zhì)有關(guān).同時觀察機(jī)械腿足部在這一階段的速度變化(見圖7(a)),足部速度的波形和最大速度基本一致,但振動頻率隨著足部質(zhì)量增大而逐漸減小,呈現(xiàn)出類似彈簧振子系統(tǒng)的動力學(xué)特性.

單足機(jī)器人在顆粒場上的跳躍行為會引發(fā)足底和顆粒場間的振動效應(yīng),進(jìn)行動力學(xué)建模分析具有較高復(fù)雜性,采用ADAMS和EDEM 聯(lián)合仿真多體系統(tǒng)和離散元的剛-散耦合效應(yīng)在目前具有更高的準(zhǔn)確性.為了分析足部的形狀設(shè)計在跳躍過程中的影響,設(shè)計一系列相同橫截面積不同錐角的同材質(zhì)圓錐底足部(直徑20mm,上半部高度為5 mm,下半部圓錐與水平面夾角在0°～ 50°分布).在壓縮沙土階段,選擇足部速度最大的時刻展示,此時足部下壓速度同樣約為0.1 m/s(見圖7(b)).觀察發(fā)現(xiàn),雖然錐形足底更利于破開沙土,但足底紅色顆粒場固結(jié)區(qū)的形狀并沒有太多變化,只是一部分被錐形足部所替代,這也與經(jīng)典土力學(xué)計算中連續(xù)體沙土受剪力分層的情況一致,進(jìn)一步論證這種分層更依賴于沙土本身物理性質(zhì);而當(dāng)足底與水平面錐角過大(圖7中45°和50°傾角所示),達(dá)到甚至超過了顆粒場固結(jié)區(qū)域本身的體積時,觀察到足底表層只會附加一層速度大致相近的顆粒層,更多的顆粒區(qū)域是直接被錐形足底所破開,此時可以認(rèn)為足底固結(jié)區(qū)完全被錐形足部取代.沙土破壞分層的改變,反應(yīng)在足底受力后的速度波動上(見圖7(b)),則是足底速度的波動頻率并沒有和圓柱形足部一樣,隨著足底的質(zhì)量增加而減小,當(dāng)圓錐水平傾角超過35°時,速度的振動頻率反而隨著質(zhì)量增大產(chǎn)生一定增大,振動特性出現(xiàn)異常.

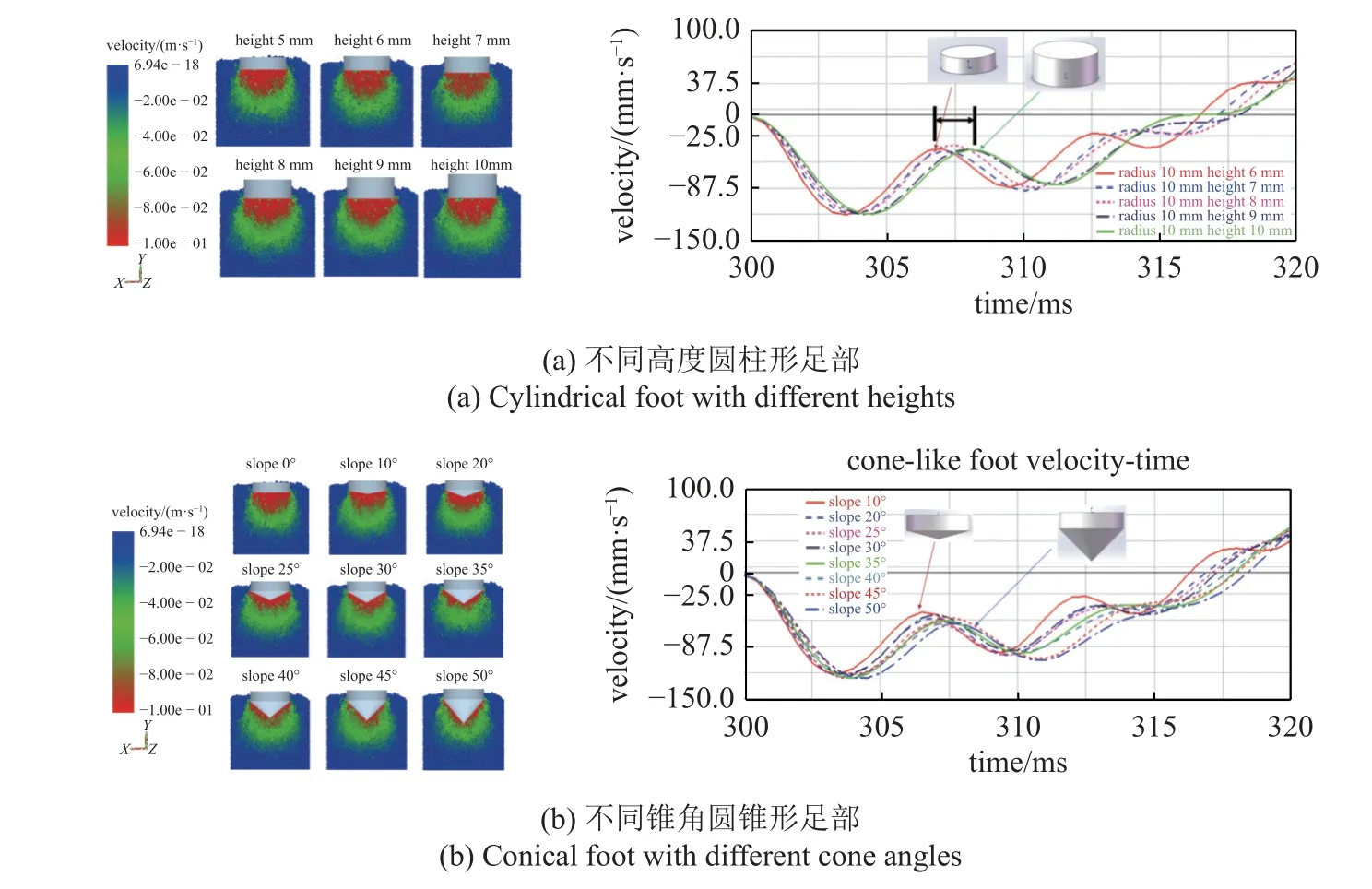
圖7 顆粒場分層和足部在壓縮顆粒場階段速度變化Fig.7 Stratification diagram of the particle field,and foot velocity variation in the stage of compressing particle field

結(jié)合足底的質(zhì)量效應(yīng)和形狀設(shè)計來分析足底設(shè)計對跳躍效果的影響(見圖8),可以觀察到,當(dāng)足底在整個系統(tǒng)中的質(zhì)量占比較小時,桿身跳躍高度與足底質(zhì)量呈良好的線性關(guān)系,跳躍高度與圓柱形足底體積的比例系數(shù)約為kclin=-6×103m-2,而與圓錐形足底體積的比例系數(shù)約為kcone=-7×103m-2.在相同質(zhì)量的情況下,圓錐形足部的跳躍高度略低于圓柱形足部,這與錐形足部破開沙土取代足底固結(jié)區(qū)顆粒場有關(guān),可以認(rèn)為固結(jié)區(qū)顆粒質(zhì)量可以進(jìn)行折算后作為附加質(zhì)量添加在足部本身的質(zhì)量上,從而使得圓柱形足部和錐形足部可以有一個進(jìn)行參照的計算質(zhì)量對比.當(dāng)跳躍相同高度時,二者間的體積具有以下關(guān)系

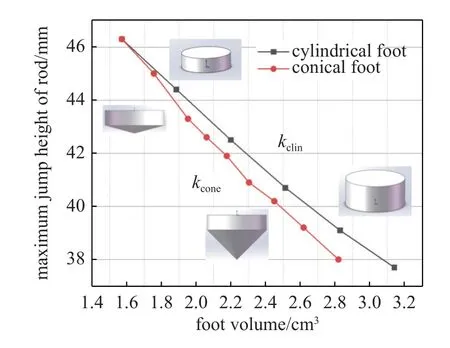
圖8 桿身最大跳躍高度與錐形、柱形足部體積關(guān)系Fig.8 The relationship between the maximum jumping height of the rod and the conical or cylindrical foot volume in the particle field

對于機(jī)器人單足系統(tǒng)設(shè)計而言,這意味著足底簡單的形狀改變可以使得機(jī)器人在可變形沙土環(huán)境中的運(yùn)動效果發(fā)生改變,從而滿足不同實際工況的需要.

4 總結(jié)

本文以探測器在行星登陸、機(jī)器人在沙土上的運(yùn)動為工程背景,研究了機(jī)械系統(tǒng)在顆粒場中的接觸動力學(xué)問題.采用離散元法和多體動力學(xué)方法對機(jī)器人單足系統(tǒng)在沙土上的跳躍問題進(jìn)行耦合動力學(xué)仿真.仿真結(jié)果表明,若采用Poncelet 公式進(jìn)行計算,對機(jī)械足侵入過程基本吻合,但在初始加速階段和減速結(jié)束階段存在較大偏差.因此基于經(jīng)典土力學(xué)Prandtl-Reissne 理論,考慮離散元仿真分析足部下壓顆粒場的過程中顆粒場的分層和演化,對描述顆粒侵入阻力的慣性力動阻力項進(jìn)行了修正,提出了一種修正的Poncelet 公式.通過與離散元仿真結(jié)果對比,說明所提出修正公式更準(zhǔn)確地計算了機(jī)械足受到的沙土侵入阻力,尤其是在機(jī)械腿足部跳躍壓縮沙土的初始階段和臨近最大深度階段.最后分析了機(jī)械腿足部的不同尺寸和形狀對沙土中跳躍效果的影響.發(fā)現(xiàn)機(jī)械腿足部與顆粒場的接觸面積會對顆粒場下壓深度、顆粒場壓縮持續(xù)時間、機(jī)械腿跳躍高度產(chǎn)生直接的單調(diào)的影響.此外,機(jī)械腿足部的體積與跳躍高度呈現(xiàn)出良好的線性關(guān)系;而同樣體積下錐形足部的跳躍高度會低于圓柱形足部.考慮足部形狀帶來的不同與足底伴隨運(yùn)動的固結(jié)區(qū)域顆粒場空間有關(guān),給出了錐形足部和柱形足部的體積對跳躍效果近似計算公式.然而,機(jī)器人單足系統(tǒng)在顆粒場上的跳躍涉及復(fù)雜的振動效應(yīng),其振動頻率、振幅衰減等動力學(xué)響應(yīng)和單足系統(tǒng)設(shè)計、顆粒場物性參數(shù)之間的深層聯(lián)系還需要進(jìn)一步挖掘.本研究將拓展剛-散耦合動力學(xué)理論,并且為新型探測器在行星土壤上運(yùn)動的系統(tǒng)設(shè)計提供技術(shù)支撐.