泊松白噪聲激勵下強非線性系統(tǒng)的半解析瞬態(tài)解1)

葉文偉 陳林聰,2) 孫建橋

*(華僑大學土木工程學院,福建廈門 361021)

?(福建省智慧基礎設施與監(jiān)測重點實驗室,福建廈門 361021)

**(加州大學Merced 分校工程學院,美國默塞德 95343)

引言

自然界和工程中普遍存在的隨機激勵,根據(jù)其概率密度分布規(guī)律,可以劃分為高斯激勵與非高斯激勵兩大類.截至目前,針對高斯激勵的相關研究已經(jīng)較為深入[1-5].然而,現(xiàn)實中大多數(shù)隨機激勵都呈現(xiàn)出固有的非高斯性質(zhì),如公路橋梁上的車輛荷載、地震和火山震導致的地面運動等,僅用高斯激勵進行建模往往是不夠的.例如,在對系統(tǒng)進行可靠性評估時,若將原本的非高斯激勵直接替換為高斯激勵,往往可能導致巨大的誤差,甚至與客觀事實相悖.因此,分析非高斯激勵下的非線性隨機振動具有重要的意義.

泊松白噪聲是一種脈沖幅值與到達時刻均為隨機的離散隨機脈沖序列.作為一種典型且重要的非高斯激勵模型,泊松白噪聲常被用于描述在科學和工程中樣本函數(shù)不連續(xù)的隨機現(xiàn)象,其動態(tài)特性已引起了廣泛的關注.當前,針對泊松白噪聲激勵下系統(tǒng)的動力學分析主要集中于穩(wěn)態(tài)響應的研究[6-10],而對于瞬態(tài)響應研究仍較為有限.然而,瞬態(tài)響應預測是非線性隨機振動研究的重要內(nèi)容之一,對于結(jié)構(gòu)的可靠性評估也具有重要價值.

當前,預測泊松白噪聲激勵下非線性系統(tǒng)的瞬態(tài)響應的方法主要是蒙特卡羅模擬法[11-12]、路徑積分法[13-15]與廣義胞映射法[16-17].這些方法均存在一些不足,例如,蒙特卡羅模擬法計算代價較為高昂,尤其模擬尾部概率密度需要大量的樣本使其平滑.路徑積分法通過對全局轉(zhuǎn)移概率密度的積分式離散化,以路徑和替代,這種近似使得計算量較大.廣義胞映射法以離散胞之間的映射關系來表征系統(tǒng)中的狀態(tài)轉(zhuǎn)移,但算法較為復雜,且易因胞流擴張降低方法的準確性.此外,上述方法所獲得的解均為數(shù)值解,在結(jié)構(gòu)優(yōu)化設計的應用方面也存在著一些局限性.因此,還需發(fā)展新的瞬態(tài)響應理論分析方法,以滿足工程實際的需要.

作為一種基于函數(shù)插值的非迭代算法,徑向基神經(jīng)網(wǎng)絡不僅可避免不必要的、冗長的計算,而且具有唯一最佳逼近,收斂速度快等優(yōu)點.近幾十年來,徑向基神經(jīng)網(wǎng)絡由于其優(yōu)越的擬合能力備受學者關注[18-19],并在諸多領域內(nèi)被廣泛應用[20-23].值得注意的是,徑向基神經(jīng)網(wǎng)絡在求解各類偏微分方程或復雜非線性方程問題[24-26]上亦展現(xiàn)出極大的優(yōu)勢.最近,有學者創(chuàng)新性地將徑向基神經(jīng)網(wǎng)絡運用于求解高斯白噪聲激勵下非線性系統(tǒng)的半解析瞬態(tài)解[27]與首次穿越問題[28],這對推動徑向基神經(jīng)網(wǎng)絡應用于非線性隨機振動的研究具有重要價值.

本文將徑向基神經(jīng)網(wǎng)絡方法進一步用于求解泊松白噪聲激勵下單自由度強非線性系統(tǒng)的非平穩(wěn)廣義Fokker-Plank-Kolmogorov(FPK)方程.首先,采用含時變待定參數(shù)的徑向基神經(jīng)網(wǎng)絡構(gòu)造廣義FPK方程的瞬態(tài)解;然后,應用有限差分法離散近似時間導數(shù)項,再結(jié)合隨機取樣技術(shù)構(gòu)造一個具有時間遞推形式的損失函數(shù).最后,時變最優(yōu)權(quán)值系數(shù)可通過拉格朗日乘子法使損失函數(shù)最小化獲得.通過兩個經(jīng)典強非線性系統(tǒng)的瞬態(tài)響應分析證實了該方法的可靠性與準確性,并分別給出了相應系統(tǒng)響應隨時間演化的規(guī)律.

1 理論概述

1.1 廣義FPK 方程

考慮一個在泊松白噪聲激勵下的單自由度強非線性系統(tǒng),其運動方程可表述為

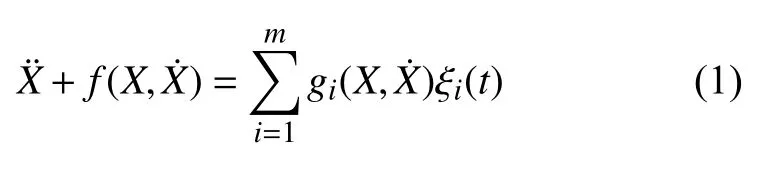
其中,f(X,) 表示阻尼和恢復力項,gi(X,) 表示隨機激勵特性,ξi(t) 表示一系列相互獨立的泊松白噪聲,其形式導數(shù)可由復合泊松過程Ci(t) 定義為

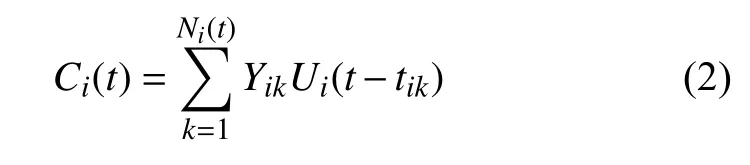
式中,Ni(t)為泊松計數(shù)過程,其平均到達率為λi;Yik表示第k個脈沖到達時刻tik的隨機振幅,且每個隨機振幅Yik與到達時刻tik相互獨立;Ui為單位階躍函數(shù).假設Yik具有相同的對稱分布,且均值為零,復合泊松過程增量的j階矩函數(shù)存在下列關系

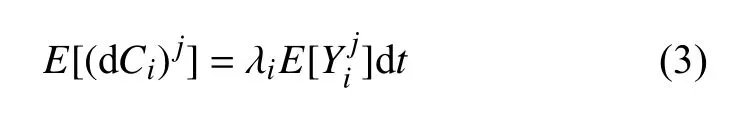
特別地,當λi為常數(shù)且Yi獨立同分布時,{C(t),t≥0}為齊次復合泊松過程.此外,當λi趨于無窮時,泊松白噪聲近似為高斯白噪聲.

令X1=X,X2=,則運動方程(1) 可轉(zhuǎn)化為如下形式隨機微分方程

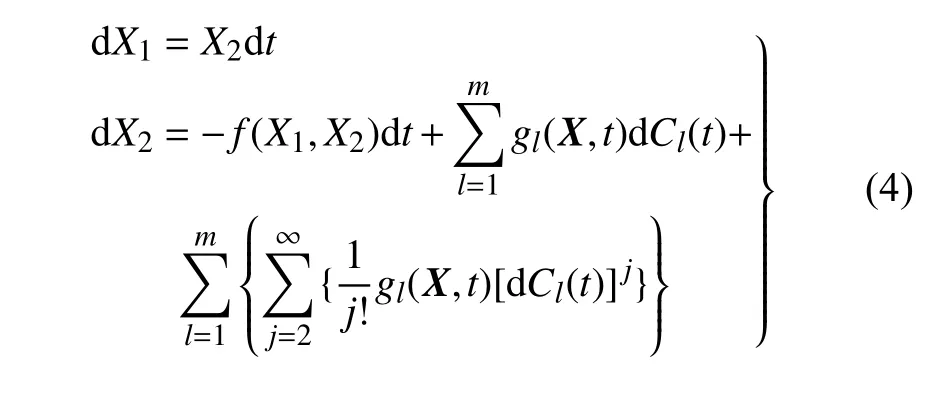
系統(tǒng)(1) 的響應向量X={X1,X2}T的轉(zhuǎn)移概率密度函數(shù)p(x,t|x0,t0) 由下列廣義FPK 方程支配

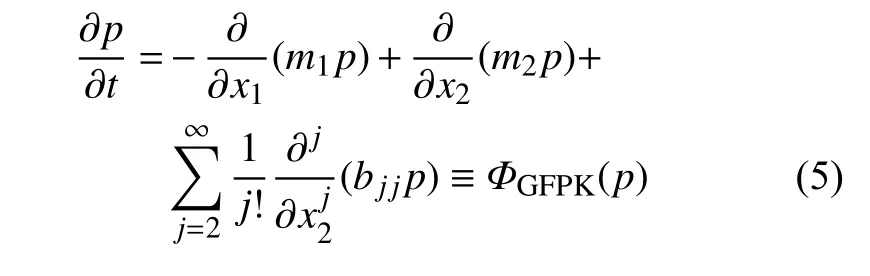
其中,ΦGFPK(·) 表示廣義FPK 方程微分算子,相應的系數(shù)m1,m2與bjj為

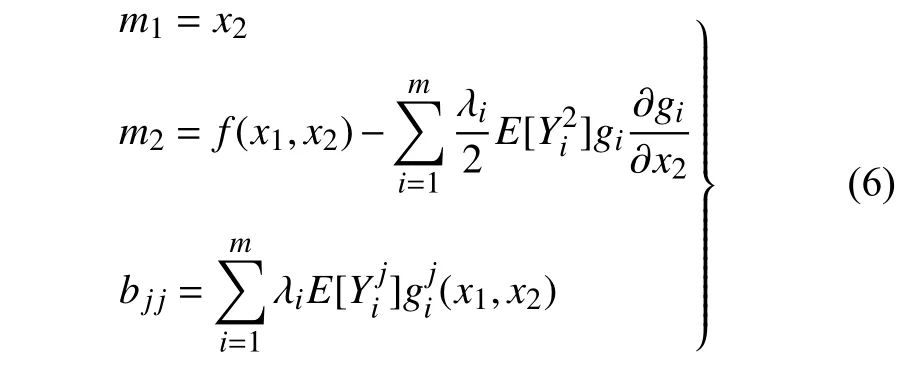
廣義FPK 方程(5) 的初始條件與邊界條件為

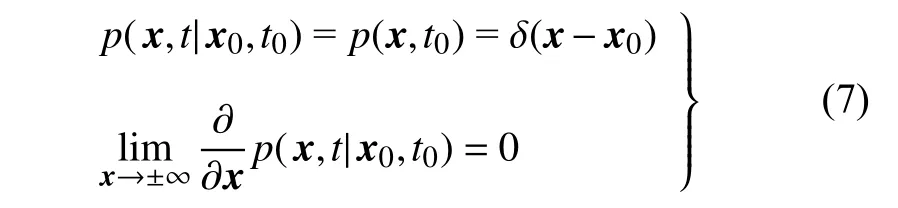
值得注意的是,廣義FPK 方程(5) 含有無窮偏微導項,即使是對于簡單的線性系統(tǒng)也無法求解,通常需要根據(jù)精度要求進行適當截斷.在下一節(jié)中,將簡要介紹徑向基神經(jīng)網(wǎng)絡方法求解廣義FPK 方程(5)的過程.

1.2 徑向基神經(jīng)網(wǎng)絡方法

假設廣義FPK 方程(5) 的瞬時解為高斯徑向基神經(jīng)網(wǎng)絡形式,即

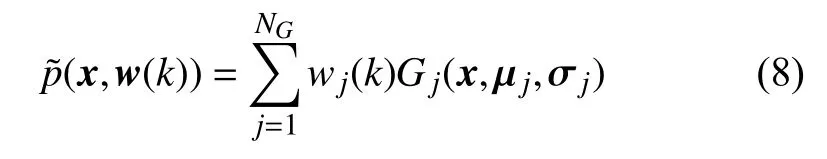
其中,x=(x1,x2),NG為激活函數(shù)的個數(shù),w(k)=(w1(k),w2(k),···,wNG(k)) 是一組時變的待定權(quán)值系數(shù),k記為時間步數(shù),時刻t=kΔτ,k=1,2,···n,Δτ為時間步長,Gj(x,μj,σj)為二元高斯函數(shù)形式的激活函數(shù),即

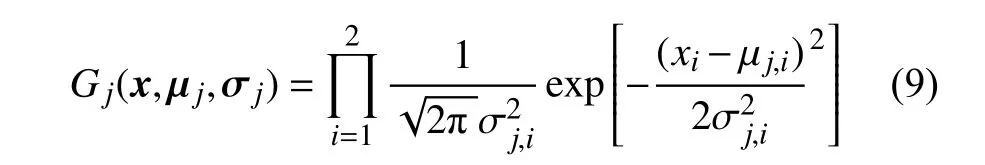
式中,σj=(σj,1,σj,2) 與μj=(μj,1,μj,2) 分別表示第j個二元高斯基函數(shù)的標準差與中心.

注意到概率密度函數(shù)(8) 與二元高斯函數(shù)(9)均滿足歸一化條件,即

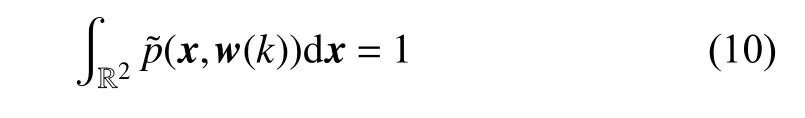
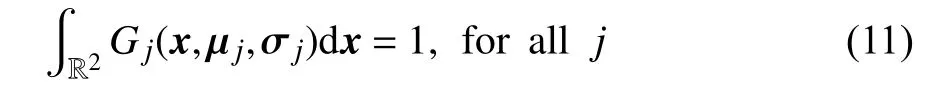
故由式(10)和式(11) 可推導出wj(k) 的約束條件為

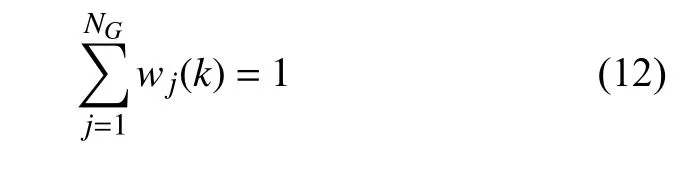
令時間步長Δτ是非常小的量,廣義FPK 方程(5) 的時間導數(shù)項可采用有限差分法近似,即

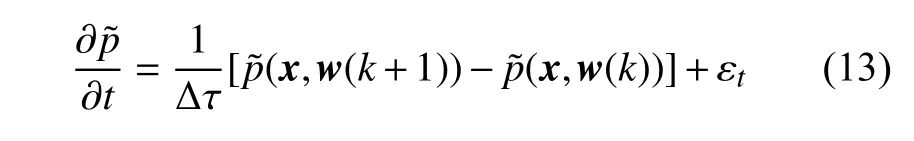
其中,εt為一階有限差分近似的截斷誤差.將試解(8)和時間導數(shù)項近似關系(13) 共同代入到廣義FPK方程(5) 中,可得到如下形式的一個局部誤差

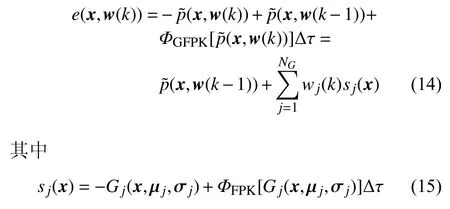
隨后,在有限域ΩS∈ R2內(nèi)采用取樣技術(shù),構(gòu)造一個損失函數(shù)Loss(w(k))

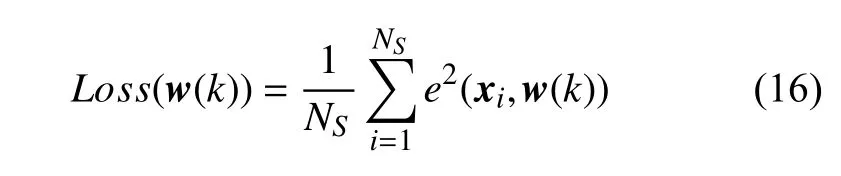
其中,NS為樣本點個數(shù).結(jié)合約束條件(12),建立一個拉格朗日函數(shù)為

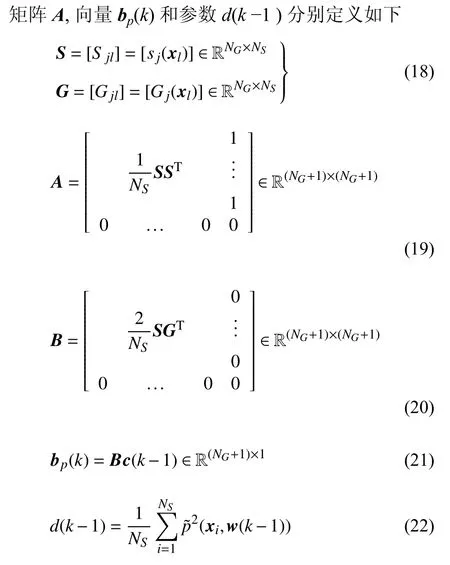
根據(jù)拉格朗日乘子法,可知式(17) 最小化的必要性條件為

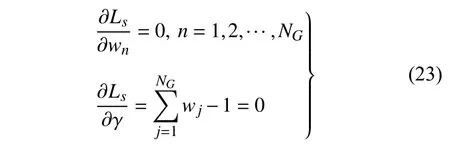
式(23) 可進一步改寫為矩陣形式如下

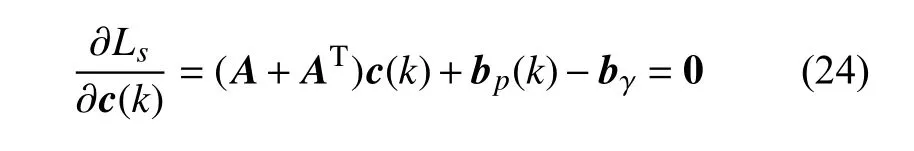
當逆矩陣(A+AT)-1存在,時變的最優(yōu)權(quán)值向量可通過式(24) 獲得,即

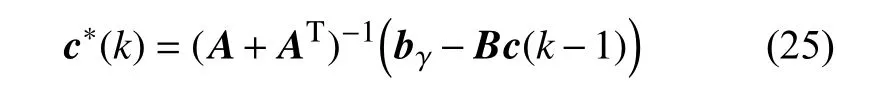
需要指出的是,該逆矩陣(A+AT)-1的存在與否在很大程度上取決于數(shù)據(jù)矩陣S[29].實踐證明當NS?NG可避免逆矩陣(A+AT)-1的奇異性[28,30].

此外,當限制所有輸出的權(quán)值系數(shù)wj(k) ≥0時,概率密度函數(shù)(8) 能夠嚴格保證非負性,這是一個充分條件.在大多數(shù)情況下,所獲得的wj(k) 是非負的,因而施加約束wj(k) ≥0對概率密度函數(shù)解的影響很小.圖1 中給出了上述算法的簡要流程圖.

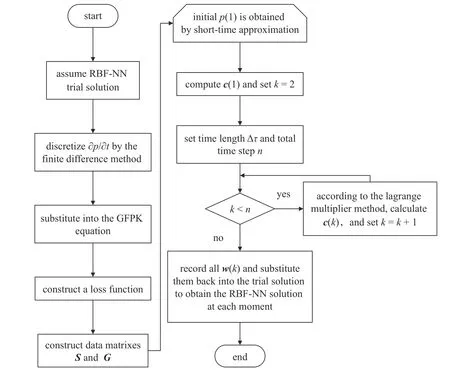
圖1 徑向基神經(jīng)網(wǎng)絡算法流程圖Fig.1 The flowchart of the RBF-NN scheme

2 算例驗證

本節(jié)將研究兩個經(jīng)典的強非線性系統(tǒng),來驗證上述方法的有效性,其中所采用的蒙特卡羅模擬樣本數(shù)均為3.0×107.

2.1 雙穩(wěn)態(tài)Duffing 系統(tǒng)

考察一個在隨機激勵下的雙穩(wěn)態(tài)Duffing 振動系統(tǒng)[31],其運動方程在狀態(tài)空間中可表示為

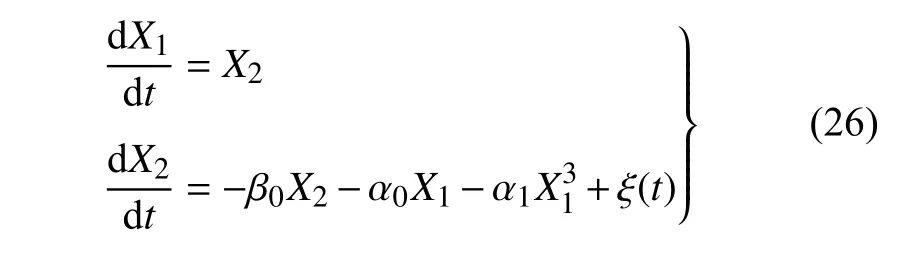
其中,系統(tǒng)參數(shù)β0=0.2,α0=-1.5,α1=4.0,ξ(t) 表示均值為零、脈沖幅值為高斯分布的泊松白噪聲,且脈沖平均達到率λ=5,方差E[Y2]=0.1.

首先,在狀態(tài)空間中選擇一個中心域ΩG=[-2,2]×[-4,4],將其均勻劃分為50×50的網(wǎng)格,取網(wǎng)格節(jié)點作為二元高斯基函數(shù)的中心(均值),則激活函數(shù)個數(shù)NG=nc×nc=50×50,并選取中心域網(wǎng)格尺寸作為二元高斯基函數(shù)的標準差,即σj=(0.08,0.16).相應地,選取比中心域稍大的樣本域為ΩS=[-3,3]×[-6,6],樣本點個數(shù)NS=ns×ns=100×100,具體參數(shù)選取可參見文獻[27-28,30],時間步長為Δτ=0.01 s.考慮到高階偏導數(shù)項對廣義FPK 方程的貢獻很小,此處僅保留前6 階偏導數(shù)項.

系統(tǒng)(26) 的初始條件為當t=0時,在(x1,x2)=(0,0) 處的概率為1 的Delta 函數(shù).可通過對動力學方程(1) 短時近似,獲得轉(zhuǎn)移概率密度函數(shù),結(jié)合路徑積分法,得到時刻t=Δτ的概率密度函數(shù)p(1),再由徑向基神經(jīng)網(wǎng)絡擬合p(1),相應的權(quán)值系數(shù)向量設為c(1).在此基礎上,可利用遞推公式(25) 得到后續(xù)任意時刻的概率密度函數(shù).

圖2 給出了t=2,2.5,3,6 s 時刻分別由徑向基神經(jīng)網(wǎng)絡方法和蒙特卡羅模擬得到的邊緣概率密度函數(shù)結(jié)果.從圖2 可以看出,系統(tǒng)(26) 響應在2～6 s這一過程中,位移概率密度函數(shù)呈雙峰,而速度概率密度函數(shù)為單峰.并且,位移概率密度函數(shù)的雙峰現(xiàn)象逐漸有所抑制,但仍維持雙峰狀態(tài),意味著在泊松白噪聲激勵下系統(tǒng)(26) 易發(fā)生小偏移.徑向基神經(jīng)網(wǎng)絡解的均方根誤差分別為3.895×10-3,2.714×10-3,1.815×10-3與1.246×10-3.由圖2 也可知徑向基神經(jīng)網(wǎng)絡結(jié)果與蒙特卡羅模擬結(jié)果高度吻合.此外,徑向基神經(jīng)網(wǎng)絡算法所運行的總時間僅為54.65 s,遠遠小于蒙特卡羅模擬所需時間2.5 h.

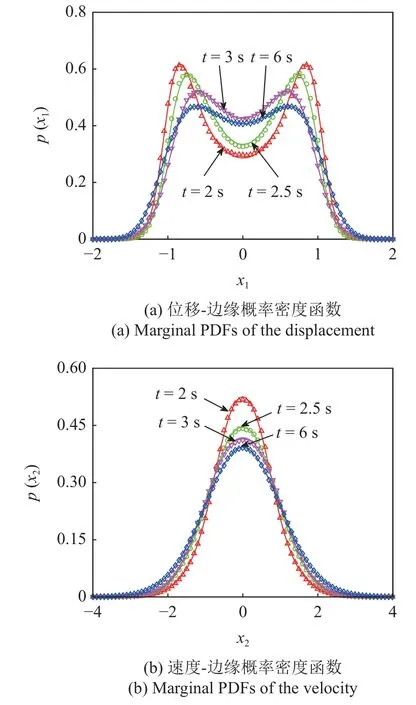
圖2 不同時刻系統(tǒng)(26) 的邊緣概率密度函數(shù)(實線:徑向基神經(jīng)網(wǎng)絡解,符號:蒙特卡羅模擬結(jié)果)Fig.2 Marginal PDFs of system(26) at different time(lines:RBF-NN solutions,symbols:MCS results)

圖3(a)和圖3(b)分別給出了本文算法所獲得的位移概率密度函數(shù)演化曲面與等值曲線圖,從中可以看出該系統(tǒng)響應的演化規(guī)律.另外,從圖3 也可以看出,當t=6 s 時,系統(tǒng)(26) 的響應接近于穩(wěn)態(tài),此時系統(tǒng)的聯(lián)合概率密度函數(shù)如圖4(a)和圖4(b)所示,概率密度函數(shù)呈現(xiàn)較為陡峭的雙峰現(xiàn)象,但即便如此,徑向基神經(jīng)網(wǎng)絡仍能近乎完美地捕捉其響應的強非線性特征.

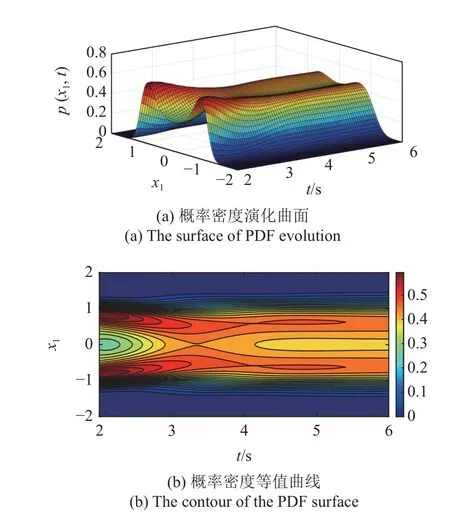
圖3 系統(tǒng)(26) 的位移概率密度函數(shù)演化Fig.3 The displacement PDF evolution of system(26)

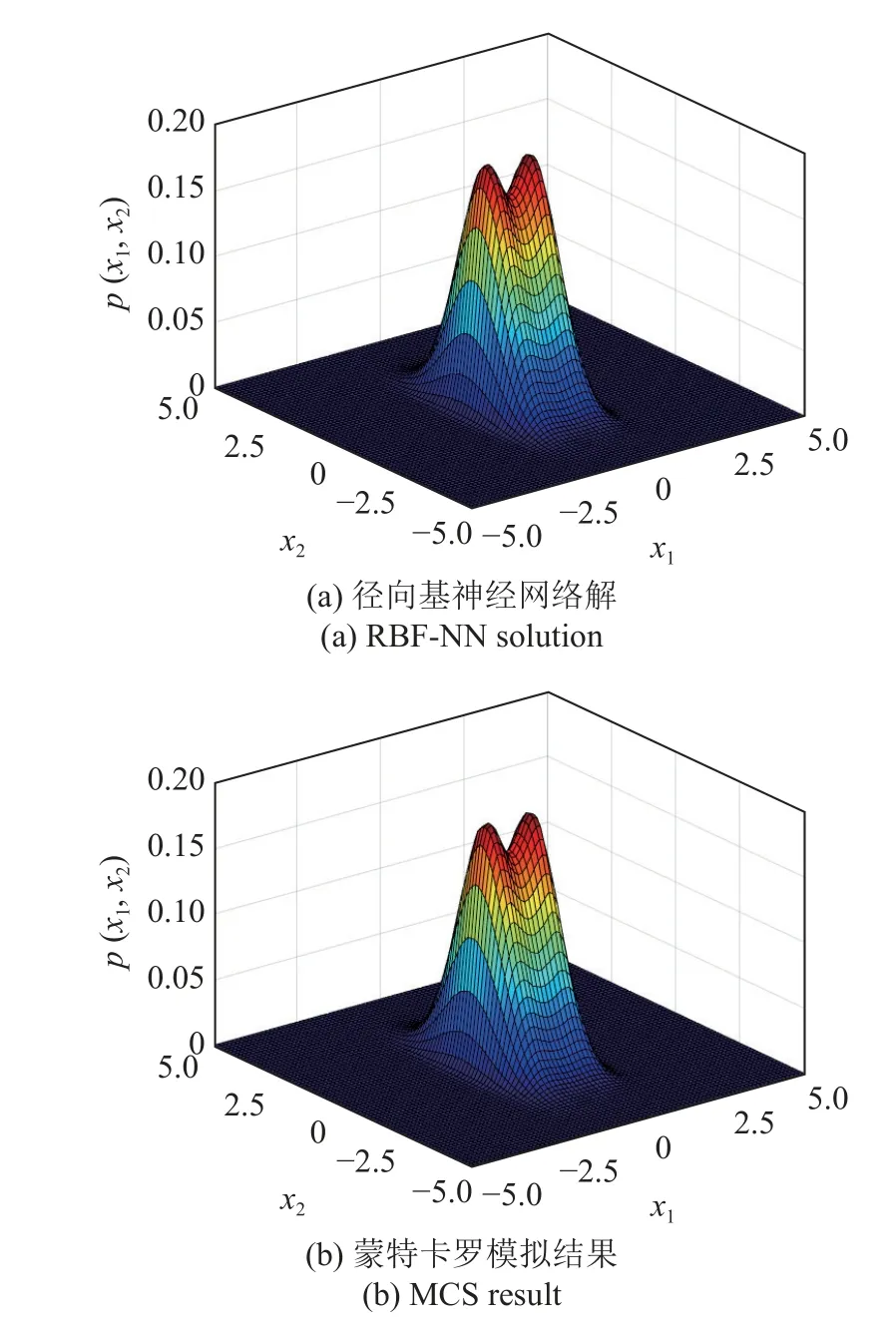
圖4 當t=6 s 時系統(tǒng)(26) 的聯(lián)合概率密度函數(shù)Fig.4 The joint PDF of system(26) at t=6 s

為了進一步了解所提出的算法,在此探究不同中心域網(wǎng)格數(shù)的劃分對計算結(jié)果的影響.保持興趣域大小不變,選取中心域網(wǎng)格尺寸作為二元高斯函數(shù)的標準差,且NG=nc×nc.根據(jù)算法,所獲得的各時刻概率密度函數(shù)相對于蒙特卡羅模擬結(jié)果的均方根誤差及計算時間如圖5 所示,在一定的范圍內(nèi)提高網(wǎng)格點數(shù),精度會有一定的提高,但是增加到一定程度后,精度提高并不明顯.然而,過多的網(wǎng)格點數(shù)會導致計算量大大增加.

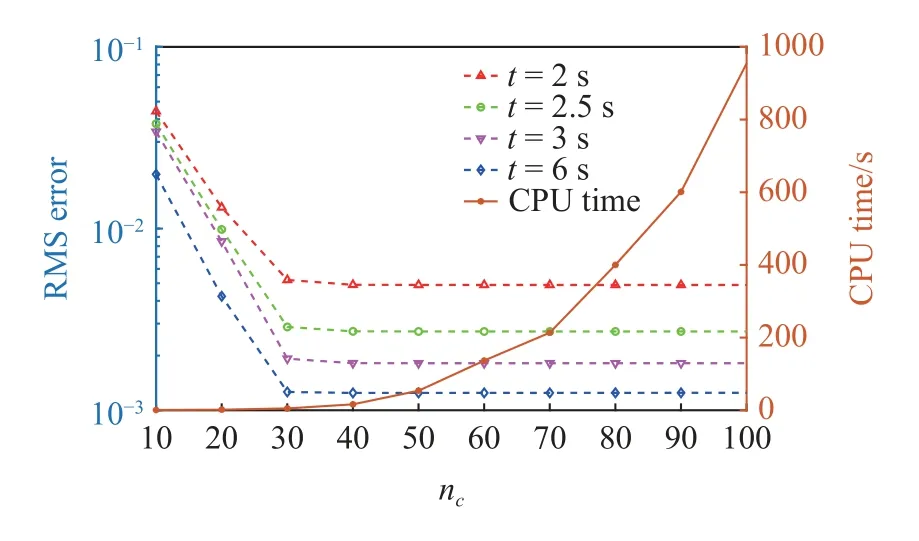
圖5 不同中心域網(wǎng)格數(shù)對算法的均方根誤差與計算時間的影響Fig.5 The effect of different number of meshes in the central domain on the root mean square(RMS) error and CPU time of the algorithm

2.2 三穩(wěn)態(tài)Van der Pol-Duffing 系統(tǒng)

考察一個在泊松白噪聲激勵下的三穩(wěn)態(tài)Van der Pol-Duffing 系統(tǒng)[32],其在狀態(tài)空間中的運動方程形式如下

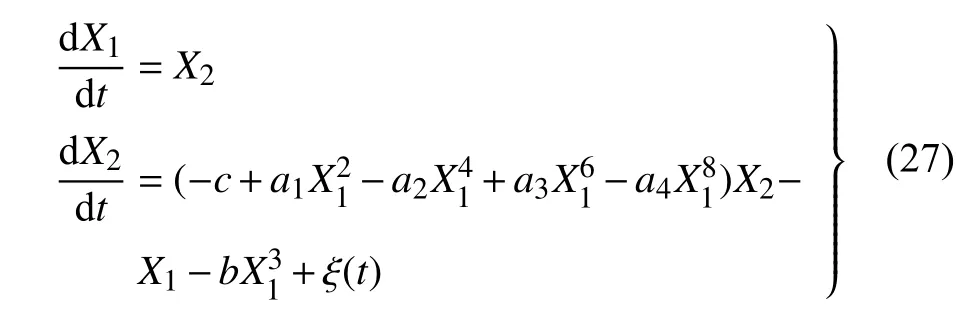
其中,系統(tǒng)參數(shù)設置為:c=0.116,a1=1.51,a2=2.85,a3=1.693,a4=0.312,b=2.0.ξ(t)為零均值泊松白噪聲,其脈沖幅值呈高斯分布,且脈沖平均達到率λ=5,方差E[Y2]=0.02.

類似地,在狀態(tài)空間中選擇中心域ΩG=[-2.5,2.5]×[-5,5],將其均勻劃分為80×80的網(wǎng)格,取網(wǎng)格節(jié)點作為二元高斯函數(shù)的中心(均值),即NG=80×80,并采取中心域網(wǎng)格尺寸作為二元高斯基函數(shù)的標準差,即σj=(0.062 5,0.125).相應地,樣本域ΩS=[-3.75,3.75]×[-7.5,7.5],樣本點個數(shù)NS=160×160.時間步長為Δτ=0.01 s.同樣,廣義FPK 方程也截斷至第6 階偏導數(shù)項.

利用本文算法,分別計算了系統(tǒng)(27)在t=0.01～80s 時刻的瞬時概率密度函數(shù).部分時刻下的瞬時概率密度函數(shù)如圖6 所示.當t=10,20,40和80s 時,相應的徑向基神經(jīng)網(wǎng)絡解的均方根誤差分別為8.730×10-4,3.157×10-4,6.752×10-4和6.816×10-4.由圖6 可知,徑向基神經(jīng)網(wǎng)絡解與蒙特卡羅模擬數(shù)據(jù)同樣非常吻合,展現(xiàn)了其較強的擬合能力;系統(tǒng)響應概率密度函數(shù)隨著時間演化,由最先的單峰向逐漸演化為三峰.此外,本算例的蒙特卡羅模擬所需時間遠超過6.0h,而徑向基神經(jīng)網(wǎng)絡算法計算總時間僅需1900.65 s,具有非常高的計算效率.

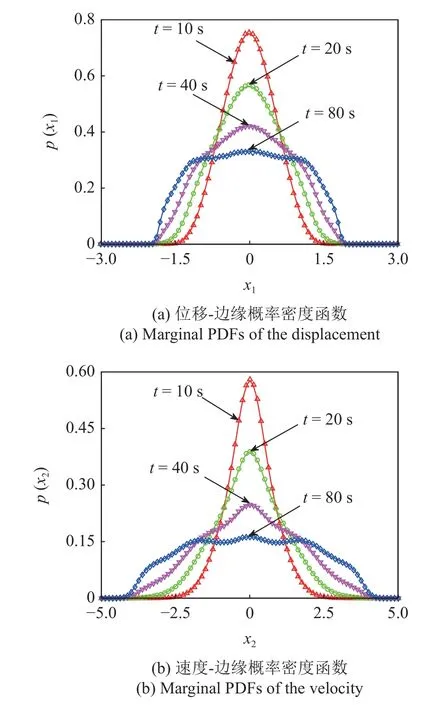
圖6 不同時刻系統(tǒng)(27) 的邊緣概率密度函數(shù)(實線:徑向基神經(jīng)網(wǎng)絡解,符號:蒙特卡羅模擬結(jié)果)Fig.6 Marginal PDFs of system(27) at different time(lines:RBF-NN solutions,symbols:MCS results)

圖7(a)和圖7(b) 給出了本文方法所獲得的位移概率密度函數(shù)演化曲面與等值曲線.從圖7 可以看出該系統(tǒng)響應的演化規(guī)律,位移的概率密度函數(shù)由單峰向多峰演化,并呈向兩邊擴散的趨勢,且當t=80s 時,系統(tǒng)(27) 的響應接近于穩(wěn)態(tài),此時系統(tǒng)響應的聯(lián)合概率密度函數(shù)如圖8 所示,呈復雜的“外筒內(nèi)錐”形,響應的非線性特征明顯且較為復雜.對比可知,徑向基神經(jīng)網(wǎng)絡解與蒙特卡羅模擬結(jié)果相當一致,所提方法在處理此類復雜非線性問題時也能達到較好的擬合效果.

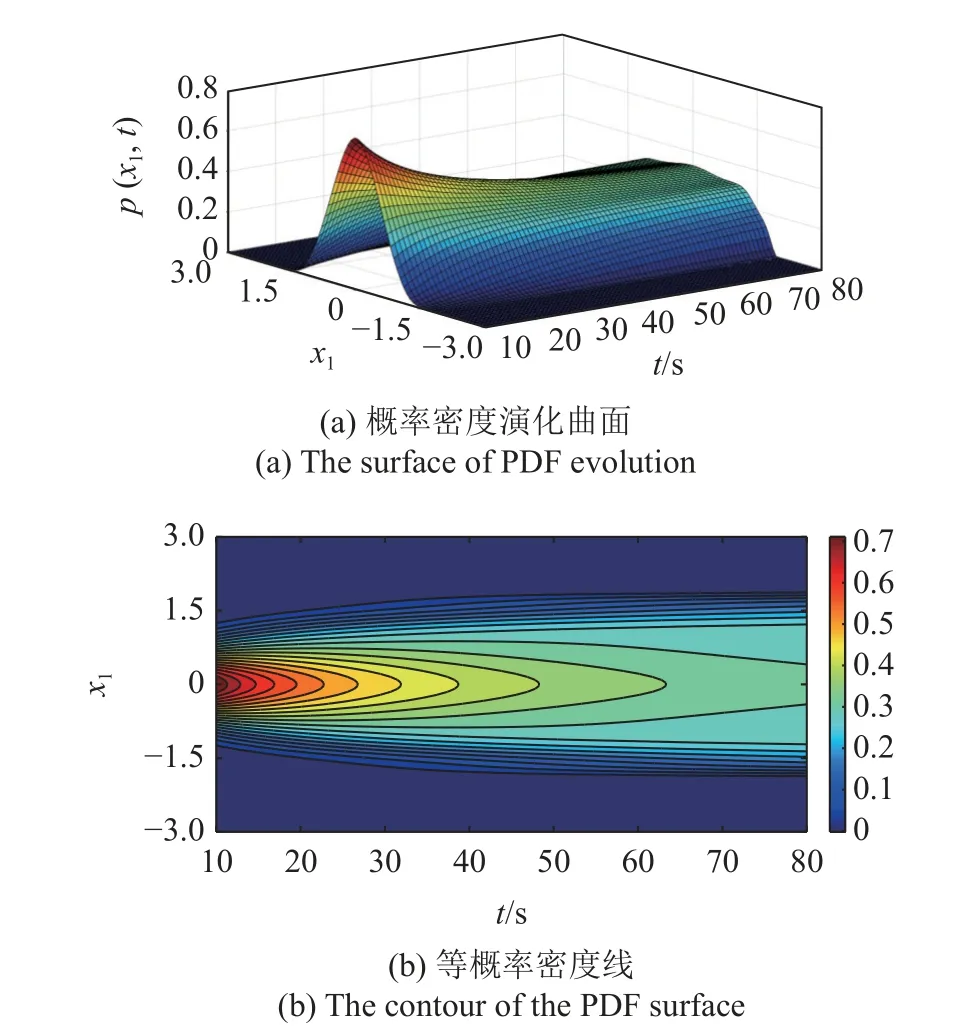
圖7 系統(tǒng)(27) 的位移概率密度函數(shù)演化Fig.7 The displacement PDF evolution of system(27)

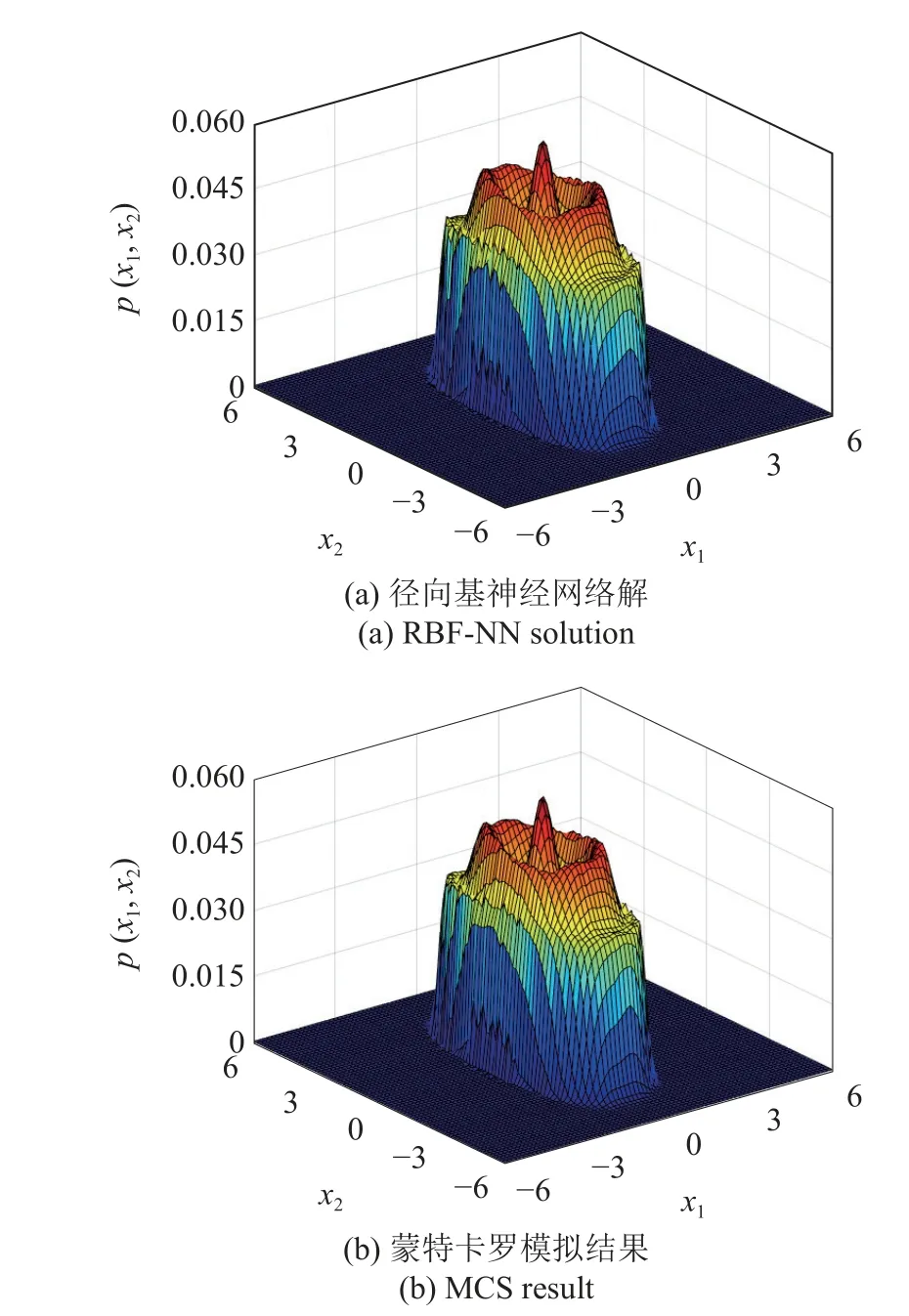
圖8 當t=80s 時系統(tǒng)(27) 的聯(lián)合概率密度函數(shù)Fig.8 The joint PDF of system(27) at t=80s

3 結(jié)論

綜上所述,本文所提出的徑向基神經(jīng)網(wǎng)絡半解析方法應用于單自由度強非線性系統(tǒng)在泊松白噪聲激勵下的瞬態(tài)響應分析是切之有效且具有廣闊前景的.兩個不同的強非線性系統(tǒng)實例證明了該方法的適用性.該方法獲得的半解析瞬態(tài)解與相應的蒙特卡羅模擬數(shù)據(jù)相比展現(xiàn)了相當高的精度,兼具較高的計算效率.系統(tǒng)瞬態(tài)響應的復雜非線性特征能夠被很好地捕捉,從而準確預測泊松白噪聲激勵下非線性系統(tǒng)響應的時間演化規(guī)律,為結(jié)構(gòu)動力反應分析與可靠度設計提供重要依據(jù).更重要的是,不同以往分析方法所獲得的數(shù)值解,本文方法所獲得的高精度瞬態(tài)解為半解析形式,不僅可作為基準解檢驗其他非線性隨機振動理論方法的精度,而且對結(jié)構(gòu)的優(yōu)化設計同樣存在重要的應用價值.當然,所提方法仍存在一定的局限性,在推廣高維解法時難免受“維數(shù)災”的影響,使得數(shù)據(jù)矩陣高度密集.為此,進一步結(jié)合降維方法,或相關數(shù)據(jù)點的優(yōu)化算法諸如稀疏矩陣、遺傳算法等是十分必要的.