半群 的格林（星）關系及富足性

陳浩林，羅永貴，高榮海

（貴州師范大學 數學科學學院，貴州 貴陽 550025）

設S是一個半群，對任意a,b∈S，如果a,b所生成的主左理想相等，即S1a=S1b，則稱a,b有L關系，記為aLb；如果a,b所生成的主右理想相等，即aS1=bS1，則稱a,b有R關系，記為aRb；如果a,b所生成的主理想相等，即S1aS1=S1bS1，則稱a,b有J關系，記為aJb；如果aLb且aRb，則稱a,b有H關系，即H=L∩R；記D為L與R的上確界，即D=L∨R。易見，L,R,H,D,J都是半群S上的等價關系，統稱為格林等價關系。在半群S上定義等價關系L*,R*,H*,D*,J*。aL*(R*)b當且僅當在包含半群S的一個半群M上aL(R)b；D*=L*∨R*，H*=L*∩R*；aJ*b當且僅當在包含半群S的一個半群M上aJb。將上述五個等價關系統稱為半群S上的格林（星）等價關系。對任意a,e∈S，若存在b∈S使得aba=a，則稱a為半群S的正則元，半群S中的所有正則元之集記為Reg，若 Reg(S)=S，則稱半群S為正則半群。若e2=e，則稱e為半群S的冪等元，半群S的所有冪等元之集記為 E(S)。顯然，冪等元一定是正則元，但正則元不一定是冪等元。若半群S的每個L-類，R-類都至少包含一個冪等元，則稱半群S為富足半群。

關于格林（星）關系及半群富足性的研究是變換半群的研究熱點之一。文獻［1］將格林關系進行推廣，獲得了廣義格林關系，并且闡述了格林關系的來龍去脈；文獻［2］驗證了變換半群的完全正則性及超富足性；文獻［3］刻劃了半群CPOn(A) 的格林關系；文獻［4-6］討論了幾類半群的格林等價關系及正則性；文獻［7］得到了半群的格林（星）等價關系及富足性；文獻［8］給出了半群的格林星關系及富足半群的定義。在文獻［1-8］的基礎上研究半群的格林（星）關系及非正則富足性。

1 預備知識

定義1 設A，B是Xn的兩個非空子集，若max A＜minB，則稱集合A小于集合B，記為A＜B。

設Xn={1,2,…,n}，對任意的x∈Xn，記Ix={y∈Xn:1≤y≤x}。Tn,Pn,Sn分別是Xn上的全變換半群，部分變換半群，對稱群。設α∈Tn，對任意x,y∈Xn,xα≤yα，則稱α是保序變換。分別用On,POn表示TnSn,PnSn上的所有保序變換之集。令SPOn=POnOn。對 1≤k≤n，記={α∈SPOn:?x∈dom(α),x≤k?xα≤k}。

其中，A1＜A2＜…＜Ar,A1∪A2∪…∪Ar≠Xn，a1＜a2＜…＜ar(1≤r≤n-1)

Ap∩Ik≠?(1≤p≤i)，Aq∩Ik=?(i+1≤q≤r)，as∈Ik(1≤s≤j)，at?Ik(j+1≤t≤r)。

設α∈，dom (α)和im(α)分別表示α的原像集和像集。記Ker(α)={(x,y)∈dom(α)×dom(α):xα=yα}。則Ker(α)為Xn上的等價關系，稱為α的核。

定義2 設 1≤k≤n，在半群上定義等價關系～*：α～*β當且僅當|im(α)|=|im(β)|。

文中未定義的術語及符號參見文獻［9-10］。

引理1［9］在有限半群S 上有D=J

反之，假設Ker(α)=Ker(β)，Ψα(k)=Ψβ(k)。不妨設

推論2設 1≤k≤n，α，β∈，且α，β是正則元，則：

（i）αLβ當且僅當im(α)=im(β)

（ii）αRβ當且僅當Ker(α)=Ker(β)

（iii）α Dβ當且僅當|im(α)|=|im(β)|且|ψα(k)|=|ψβ(k)|

證明：必要性顯然成立。下證充分性

引理 2 設S 是半群，a,b∈S，則

（1）aL*b當且僅當對任意x,y∈S，

ax=ay?bx=by；

（2）aR*b當且僅當對任意x,y∈S，

xa=ya?xb=yb；

定理 5 設 1≤k≤n，α，β∈，則

（1）α L*β 當且僅當im(α)=im(β)；

（2）α R*β 當且僅當Ker(α)=Ker(β)；

證明：（1）α L*β，不妨設

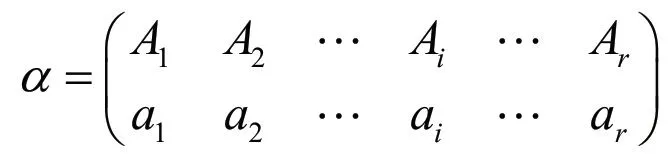
其中，

ap∈Ik,aq?Ik,1≤p≤i,i+1≤q≤r。

取1 為Xn上的恒等變換，令

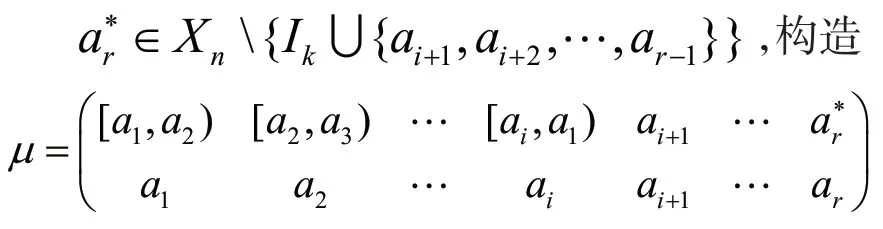
顯然，μ∈，im (α)=im(μ)且α1=αμ，由引理2 可得β1=βμ，從而im(β)=im(β)μ?im(μ)=im(α)。同理，im(α)?im(β)。因此im(α)=im(β)。

反之，若im(α)=im(β)，因為在部分變換半群Pn中有αLβ，從而αL*β。

（2）若αR*β，設

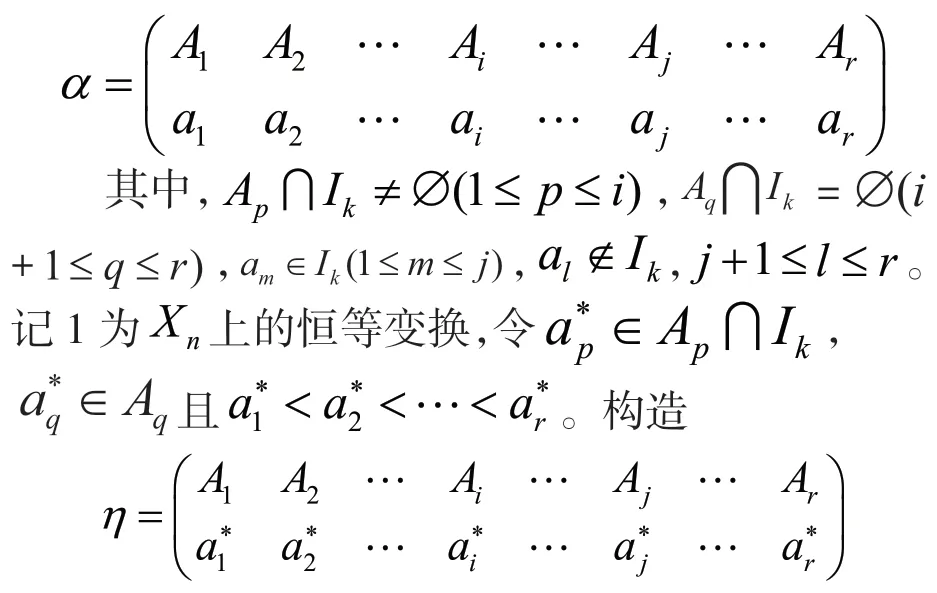
顯然，η∈，Ker(α)=Ker(η)且1α=ηα，由引理2 可得 1β=ηβ。對任意的(x,y)∈Ker(α)，有xα=yα，則xη=yη，從而xβ=(xη)β=(yη)β=yβ，因此Ker(α)?Ker(β)。同理可得Ker(β)?Ker(α)。因此Ker(α)=Ker(β)。

反之，若Ker(α)=Ker(β)，因為在部分變換半群Pn中有αRβ，從而αR*β。

定理 6～*=L*?R*?L*=R*?L*?R*=D*

證明：設α,β∈，若α～*β，不妨設|im(α)|=|im(β)|=r，分為以下兩種情形

情形1：|ψα(k)|=|ψβ(k)|=s，設

其中，ap，bp∈Ik，aq，bq?Ik，·1≤p≤s，s+1≤q≤r，令

其中，ap，bq∈Ik，1≤p≤s，·1≤q≤m，al，bh?Ik，s+1≤l≤r，m+1≤h≤r。

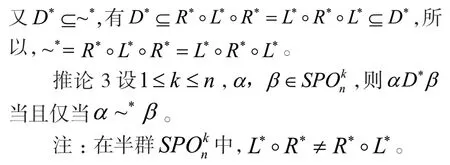
例 1 設n=6,k=3,r=3,令