A NOTE ON MEASURE-THEORETICEQUICONTINUITY AND RIGIDITY*
Chiyi LUO(羅熾逸)Yun ZHAO (趙云)*
School of Mathematical Sciences and Center for Dynamical Systems and Differential Equations Soochow University,Suzhou 215006,China E-mail: 20194207005@stu.suda.edu.cn; zhaoyun@suda.edu.cn

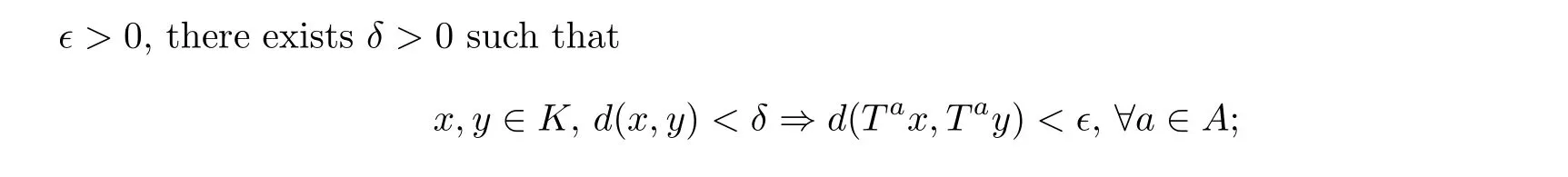
(ii) a function f ∈L2(μ) is called μ-A-equicontinuous if, for any τ > 0, there exists a compact subset K ?X with μ(K)>1-τ such that {f ?Ta:a ∈A} is equicontinuous on K,that is, for any ?>0, there exists δ >0 such that
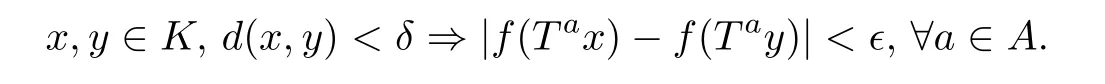
Given a TDS (X,T), a T-invariant measure μ and f ∈L2(μ), Cai [1] proved the following results which gave the relations between measure-theoretic equicontinuity and rigidity of a TDS(see[4,6-8]and references therein for more descriptions of the relations between the topological equicontinuity and rigidity of a TDS):
Theorem 1.2 ([1, Corollary 3.9]) Let (X,T) be a TDS and μ be a T-invariant measure.Then (X,B,μ,T) is rigid if and only if there exists a subsequence A = {ai: i ∈N} of N such that (X,T) is μ-A-equicontinuous.
Theorem 1.3 ([1, Corollary 3.11]) Let (X,T) be a TDS, μ be a T-invariant measure,and f ∈L2(μ). Then f is rigid if and only if there exists a subsequence A={ai: i ∈N} of N such that f is μ-A-equicontinuous.
The notion of μ-mean equicontinuity was introduced in [3], where it was proved that if an MPS (X,B,μ,T) is ergodic, then it has discrete spectrum if and only if it is μ-mean equicontinuous. Later, Huang et al. [5] introduced a similar notion called μ-equicontinuity in the mean and proved that these two notions are equivalent; moreover, they proved that a general MPS (X,B,μ,T) has discrete spectrum if and only if it is μ-mean equicontinuous (see [10] for another proof). Following this idea, Cai [1] introduced the notion of measure-theoretic mean equicontinuity along some subsequence A of N.
Definition 1.4 Given a TDS (X,T) and a subsequence A={ai:i ∈N}?N, let μ be a T-invariant measure. Then,
(i) (X,T)is calledμ-A-equicontinuous in the mean if,for each τ >0,there exists a compact subset K ?X with μ(K)>1-τ such that for any ?>0, there exists δ >0 such that
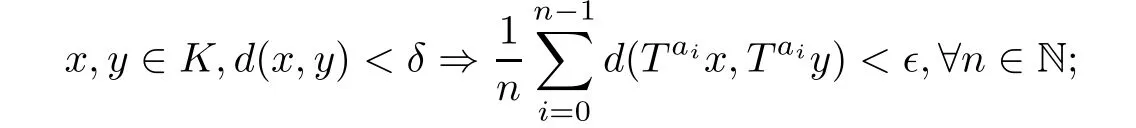
(ii) a function f ∈L2(μ) is calledμ-A-equicontinuous in the mean if, for each τ >0, there exists a compact subset K ?X with μ(K)>1-τ such that for any ?>0, there exists δ >0 such that

In a similar fashion, we say that a TDS (X,T) is μ-A-mean equicontinuous if, for each τ >0, there exists a compact subset K ?X with μ(K)>1-τ such that
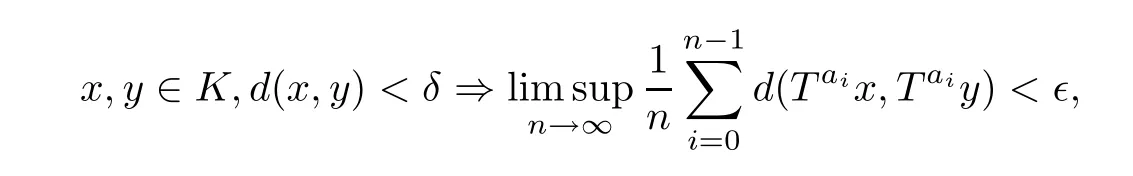
and that a function f ∈L2(μ) is μ-A-mean equicontinuous if, for each τ > 0, there exists a compact subset K ?X with μ(K)>1-τ such that
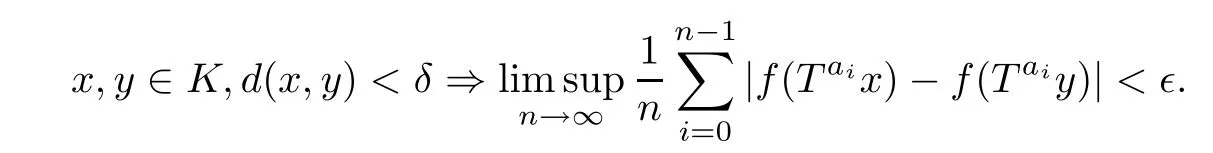
In fact,the notions ofμ-A-mean equicontinuous andμ-A-equicontinuous in the mean are equivalent with respect to a TDS or a function f;see Theorem 4.2 and Theorem 4.8 in[1]for detailed proofs.
In [1], Cai obtained the following relations between measure-theoretic mean equicontinuity and rigidity:
Theorem 1.5 ([1, Theorem 4.5]) Let (X,T) be a TDS and μ be a T-invariant measure.If there exists a subsequence A = {ai: i ∈N} of N with D(A) > 0 such that (X,T) isμ-A-equicontinuous in the mean, then (X,B,μ,T) is rigid.
Theorem 1.6 ([1, Theorem 4.9]) Let (X,T) be a TDS, μ be a T-invariant measure and f ∈L2(μ). If there exists a subsequence A = {ai: i ∈N} of N with D(A) > 0 such that f isμ-A-equicontinuous in the mean, then f is rigid.
In [1], Cai asked the question of whether or not the condition D(A) > 0 in the above two theorems is necessary. In fact, this is the main obstacle to giving the equivalence between measure-theoretic mean equicontinuity and rigidity. In this paper, we show that the condition D(A)>0 is redundant. Furthermore, we obtain the following results:
Theorem 1.7 Let (X,T) be a TDS and let μ be a T-invariant measure. Then the following statements are equivalent:
1. (X,B,μ,T) is rigid, where B is the σ-algebra on X;
2. there exists a subsequence A={ai:i ∈N} of N such that (X,T)is μ-A-equicontinuous in the mean.
Theorem 1.8 Let (X,T) be a TDS, let μ be a T-invariant measure and let f ∈L2(μ).Then the following statements are equivalent:
1. f is rigid;
2. there exists a subsequence A = {ai: i ∈N} of N such that f is μ-A-equicontinuous in the mean.
In the next section, we will give detailed proofs of these two theorems.
2 Proofs of the Main Theorems

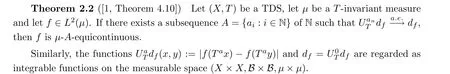
Proof of Theorem 1.7 If (X,B,μ,T) is rigid, by Theorem 1.2, there exists a subsequence A of N such that (X,T) is μ-A-equicontinuous, that is, for any τ > 0, there exists a compact subset K ?X with μ(K) > 1-τ such that {Ta: a ∈A} is equicontinuous on K,that is, for any ?>0, there exists δ >0 such that
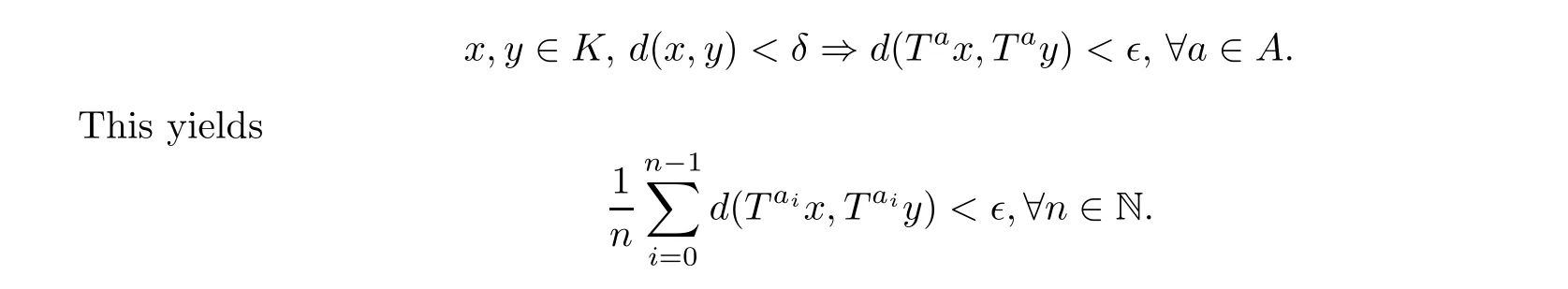
Therefore, the TDS (X,T) is μ-A-equicontinuous in the mean.
To prove the other direction, we assume, without loss of generality, that d(x,y)≤1 for all x,y ∈X. It suffices to prove that there exists a subsequence B ={bi:i ∈N} of N such that

Consequently, for every (x,y)∈Xi×Xj, we have that
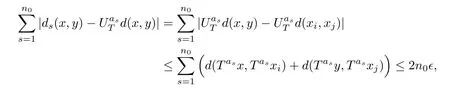

 Acta Mathematica Scientia(English Series)2022年2期
Acta Mathematica Scientia(English Series)2022年2期
- Acta Mathematica Scientia(English Series)的其它文章
- IMPULSIVE EXPONENTIAL SYNCHRONIZATIONOF FRACTIONAL-ORDER COMPLEX DYNAMICALNETWORKS WITH DERIVATIVE COUPLINGS VIAFEEDBACK CONTROL BASED ON DISCRETE TIME STATE OBSERVATIONS*
- GLOBAL SOLUTIONS TO A 3D AXISYMMETRIC COMPRESSIBLE NAVIER-STOKES SYSTEMWITH DENSITY-DEPENDENT VISCOSITY*
- COMPLETE MONOTONICITY FOR A NEW RATIO OF FINITELY MANY GAMMA FUNCTIONS*
- A NONSMOOTH THEORY FOR A LOGARITHMIC ELLIPTIC EQUATION WITH SINGULAR NONLINEARITY*
- UNDERSTANDING SCHUBERT'S BOOK (III)*
- a-LIMIT SETS AND LYAPUNOV FUNCTION FORMAPS WITH ONE TOPOLOGICAL ATTRACTOR *
