基于改進蟻群優化算法的自動駕駛多車協同運動規劃

宋佳艷，蘇圣超

（上海工程技術大學電子電氣工程學院，上海 201620）

0 概述

智能交通系統（Intelligent Transportation System，ITS）是利用數據通信傳輸、電子傳感等技術對傳統運輸系統進行改進而形成的一種信息化、智能化、社會化的新型運輸系統，對于緩解當前大中城市的交通壓力起到了關鍵作用。自動駕駛技術的不斷發展，能夠有效減少交通事故，提高通行效率［1］。多車協同規劃是自動駕駛中的重要部分，在很大程度上決定了整個交通系統的智能程度［2］。協同規劃不同于單車運動軌跡的疊加［3］，主要是要求多車在行駛過程中考慮與其他車輛及環境之間的信息，通過規避障礙物且與其他車輛保持安全距離，最終到達各自的目的地［4-5］。自動駕駛的協同規劃能夠在提高安全性的同時，減少交通擁堵［6］。由于計算復雜度隨著車輛數量增加，且需要確保車輛間的協同，因此如何在復雜交通環境中規劃多車實時運動軌跡是亟需解決的問題［7-8］。

目前，國內外學者已對自動駕駛車輛協同運動規劃展開研究。CHEN 等［9］根據優先級順序對多車輛進行規劃，將高優先級車輛視為低優先級車輛的時變障礙物，計算復雜度隨著車輛數量線性縮放，由于該方法中的優先級算法一次只規劃一輛車，因此當面對高度沖突的大規模規劃情況時，整個系統的協同能力不足。LI等［10］提出基于順序計算框架的增量約束動態優化方法，通過引入更多的避碰約束使每一個子問題比前一個子問題更難，將每一個子問題的最優解作為下一個子問題的初始解，直到得到最終解。由于該方法將原問題分散為多個部分逐步解決，因此無法確保在實際情況下能夠進行在線規劃。TAHIROVIC 等［11］提出一種基于雙層區域覆蓋的多車運動規劃算法，上層為每輛車粗略規劃行駛軌跡，下層對多車之間進行協調，為每輛車生成無碰撞軌跡。該算法由于協調過程不同時執行，因此導致了解決方案質量較差。HUANG 等［12］針對協同駕駛問題，提出一種基于人工勢場（Artificial Potential Field，APF）和模型預測的協同駕駛方法，設置成本函數，從多目標多約束優化角度出發，很好地解決了自動駕駛運動規劃問題，但該方法未考慮軌跡的實時優化。由上述研究可知，目前協同規劃能有效保證運行車輛與障礙物及其他車輛之間避免發生碰撞并保持安全距離，但車輛之間的協同能力以及在線規劃能力仍需進一步提升。

本文提出一種基于改進蟻群優化（Ant Colony Optimization，ACO）算法的自動駕駛多車協同運動規劃方法。將蟻群優化算法應用于自動駕駛車輛運動規劃中，并將多目標優化函數引入蟻群優化算法的信息素更新過程中，通過空間協同和軌跡優化的目標函數對信息素進行實時更新，同時對蟻群優化算法中的揮發因子進行自適應調整，以實現多車自動駕駛的在線協同運動規劃。

1 自動駕駛車輛運動學模型

為保證自動駕駛車輛實際行駛軌跡平滑，在進行自動駕駛運動規劃時需要滿足車輛運動學約束條件，對車輛運動學模型進行分析。自動駕駛車輛運動學模型如圖1 所示。

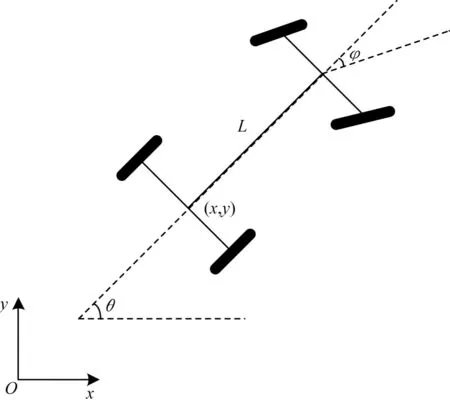
圖1 自動駕駛車輛運動學模型Fig.1 Kinematics model of autonomous driving vehicle

自動駕駛車輛運動學約束方程［13］如式（1）所示：

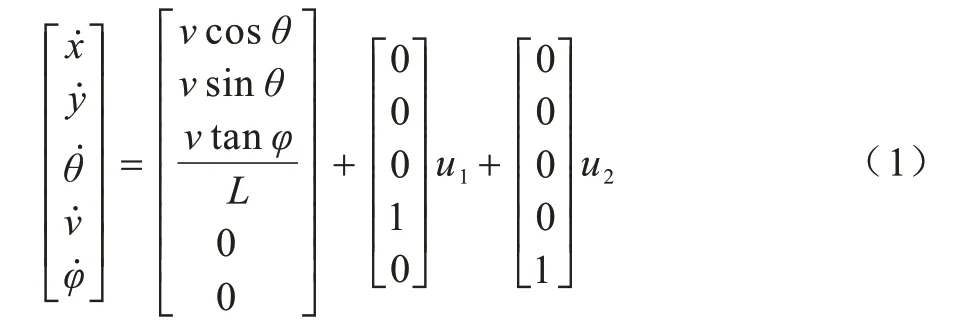
其中：(x，y)表示自動駕駛車輛后輪中點位置；φ表示轉角速度；θ表示前進方向；v表示車輛運行速度；L表示車輛前后輪軸距；u1、u2分別表示自動駕駛車輛加速度與前輪偏轉角速度。

2 改進的蟻群優化算法

蟻群優化算法［14］是指自然界中螞蟻可以在沒有任何提示的情況下找到一條最優路徑，這主要是由于螞蟻在覓食路線上會分泌信息素［15］，隨著迭代次數的增多，螞蟻會在較短的路徑上積累更多的信息素，這種信息素會在其他螞蟻面臨覓食路線選擇時發出強烈信號進行準確的路線引導，從而大幅提高后續螞蟻選擇這條路線的概率，隨著該過程不斷重復，該算法構成一個正反饋回路［16-17］。蟻群優化算法主要包括概率選擇和信息素更新2 個步驟。

2.1 概率選擇

螞蟻通過輪盤賭選擇規則［18］進行下一個方向的選擇，螞蟻k從g走向下一個位置h的概率計算如下：

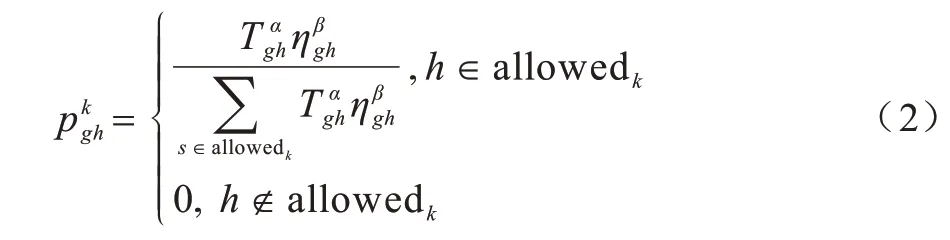
其中：Tgh為路徑(g，h)上的信息素量；allowedk為禁忌表之外螞蟻可以走的點；α為信息素因子；β為啟發因子，表示下一個節點對當前節點的影響程度。

ηgh為啟發函數［19］，計算公式如下：

其中：dgh為下一個可行節點到目標點的歐式距離。

兩個節點之間的歐氏距離定義如下：

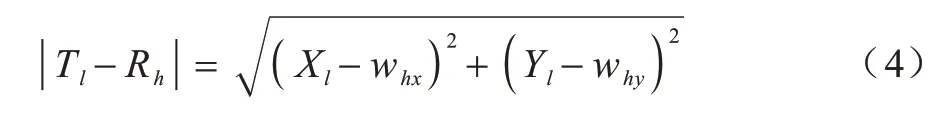
其中：Tl=(Xl，Yl)表示目標點的坐標；Rh=(whx，why)表示下一個可行節點的坐標。

2.2 信息素更新

在所有螞蟻完成一次迭代后，路徑上的信息素進行全局更新，信息素更新公式如下［20］：

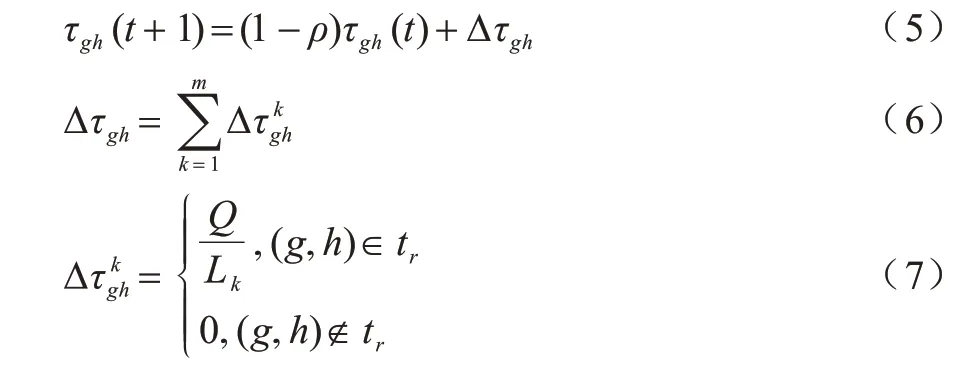
其中：ρ為信息素揮發因子，ρ∈(0，1)，(1-ρ)為信息素殘留因子；τgh(t)為當前時刻信息素濃度；Δτgh為信息素增量；為當前迭代周期螞蟻k的信息素增量；Q為常數，表示信息素強度；Lk表示循環結束時螞蟻k所走的路徑長度；tr表示螞蟻r已完成的任務集合。

將每一次迭代產生的最優解與歷史最優解進行對比，產生新的最優解，在迭代次數達到所設定值時，輸出最優路線［21］。

3 基于改進ACO 的自動駕駛多車協同規劃

采用蟻群優化算法進行自動駕駛車輛的運動規劃，根據自動駕駛車輛數量產生多個螞蟻種群，各種群相互獨立并規劃相應的路線，在規劃過程中通過多目標優化模型確保多輛汽車的協同性，對軌跡代價和空間協同約束進行數學建模，設立目標優化函數，并將目標函數應用于信息素更新規則，確保多輛自動駕駛汽車的協同安全性與軌跡平滑性。

3.1 多目標優化模型設計

3.1.1 空間協同代價與軌跡代價模型

車輛在進行運動規劃時，為保證安全性，首先應考慮車輛與障礙物之間無碰撞。假設整個協同環境中存在Nn輛車和Nobs個障礙物，設置車輛與障礙物之間的安全距離dsafe1。理想的最優軌跡應適當與障礙物保持一定的距離，當車輛與障礙物之間的距離大于安全距離時，車輛與障礙物互不影響；當車輛與障礙物之間的距離小于安全距離時，應保持距離盡可能遠。車輛與障礙物空間協同函數的計算公式如下：

其中：dik表示車輛i與障礙物k之間的距離；κ1為距離系數，表示期望車輛i遠離障礙物k的程度。

車輛與障礙物之間的空間協同代價模型建立如下：

同樣地，在考慮車輛與障礙物之間無碰撞的前提下，多車協同運動規劃要求各車輛在行駛過程中應盡量保持距離。車輛與障礙物之間的安全距離為dsafe2，車輛間空間協同函數的計算公式如下：

其 中：dij為車輛i與車輛j之間的距離；κ2為距離系數，表示期望車輛i與車輛j之間互相遠離的程度。

車輛間的空間協同代價模型建立如下：

軌跡平滑性與前輪偏轉角的變化幅度有關，通過設置軌跡平滑程度的代價模型，表示車輛i在運動時域內因車輪轉角變化而消耗的能量。軌跡代價函數的計算公式如下：

其中：φi(t)表示t時刻車輛i的前輪偏轉角；tf表示車輛到達終點的時刻。

3.1.2 目標函數優化

基于上文描述，構建自動駕駛協同控制的軌跡優化數學模型，將空間協同代價模型與軌跡代價模型進行加權匯總，如式（13）所示，建立以空間協同代價模型與軌跡代價模型為目標函數的數學模型。

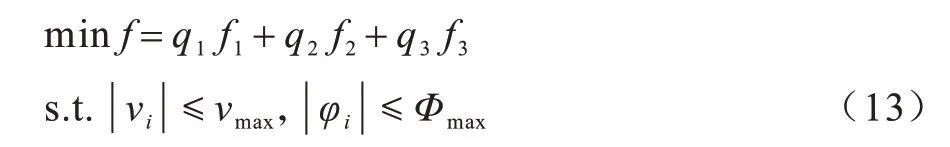
其中：f為綜 合代價；vi表 示車輛i的運行速度；vmax表示安全情況下車輛的最大運行速度；Φmax表示最大轉角速度；q1、q2、q3為各性能指標對應的權重系數，權重越大表示該部分在代價函數中越受重視，q1、q2、q3滿足非負性和歸一性

3.2 信息素更新規則改進

蟻群優化算法作為一種啟發式智能算法，通過模擬自然界中螞蟻尋找食物的過程來尋找問題的最優解［22］。螞蟻在覓食過程中會在經過的道路上釋放信息素，后續經過的螞蟻會根據所留下的信息素濃度對下一個位置進行選擇，因此信息素的分布對全局的規劃起著至關重要的作用［23］。采用蟻群優化算法進行協同規劃，信息素對各車輛起著引導作用，決定汽車的運動方向與路線，直接影響車輛間的協同能力，因此本文對信息素進行改進。

上文通過構造多目標優化函數，考慮了空間協同代價與軌跡代價，能夠確保多車自動駕駛的自適應協同能力與安全性，同時又保證了乘車人的舒適度。因此，考慮將目標函數加入蟻群優化算法的信息素更新規則中，改進的信息素更新規則如式（14）所示：

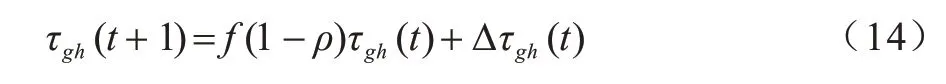
將多目標優化所涉及空間協同代價和軌跡代價模型引入信息素更新過程中，通過多目標優化函數所得的實時數據對信息素進行相應的懲罰和獎勵：若加入目標函數后的蟻群優化算法出現更優軌跡，則表示其對信息素具有正反饋，因此對信息素進行獎勵，增加信息素的導向性，即可加快算法收斂速度；若加入目標函數后得到軌跡較差，則表示對信息素具有負反饋，在信息素更新時進行懲罰，弱化最優軌跡上所積累的信息素，給予次優或較優軌跡更大的被選擇概率，提高軌跡選擇的多樣性，避免陷入局部最優。

3.3 揮發因子調整

蟻群優化算法中固定的揮發因子ρ實際上是按一種固定不變的模式確定每次的路徑選擇概率以及更新的信息量，不能很好地保證自動駕駛車輛方向選擇的靈敏度以及軌跡的最優。面對復雜多變的環境，需要提高各種群對路徑的全局搜索能力，提升算法實時性。

在蟻群優化算法中揮發因子ρ始終保持不變，表示信息素的蒸發程度，反映了螞蟻個體之間的互相影響程度。若ρ設置不合理，螞蟻可能會喪失全局搜索能力，也會影響收斂速度。當ρ過小時，信息素揮發慢，若螞蟻一開始找到的是次優路徑而非最優路徑，受信息素揮發度的影響，次優路徑的信息素逐漸積累，很難再找到最優路徑，易陷入局部最優解，影響算法的隨機性能；當ρ過大時，信息素揮發快，過多的無用搜索不利于螞蟻選擇下一個方向的路徑，搜索能力降低，收斂速度減慢。為提高自動駕駛車輛在實際運動規劃中的全局搜索能力以及收斂速度，對揮發因子的自適應更新調整如下：

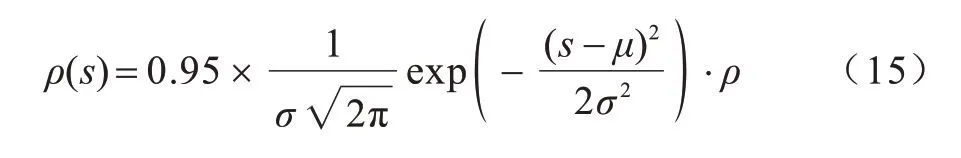
其中：ρ∈(0，1)；s為當前迭代次數，表示s服從參數σ和μ的高斯函數，σ和μ為常數。

構造的新的信息素揮發因子遵循高斯分布，可以提高螞蟻搜索的目的性以及搜索速度。高斯函數分布曲線如圖2 所示，當搜索開始時，揮發因子較小，路徑上信息素濃度對螞蟻影響較大，使得蟻群向信息素多的路徑靠攏。隨著信息素不斷更新，為避免陷入局部最優，揮發因子取得較大值，螞蟻能夠自由搜索更多路徑。在搜索后期，為加快收斂速度，揮發因子取得一個較小值。經過多次的迭代，螞蟻快速地集中于信息素濃度較高的路徑。

圖2 高斯函數分布曲線Fig.2 Gaussian function distribution curve

4 實驗與結果分析

為驗證本文方法的有效性，采用Matlab2019a 軟件進行仿真實驗，基于非結構化道路以及結構化道路場景進行運動規劃，非結構化道路是指邊緣比較規則，沒有明顯車道線的行車道路，例如園區、學校等場所內的道路，結構化道路是指具有清晰道路標志線的行車道路，例如高速公路、城市干道等道路。實驗相關參數設置如表1 所示。

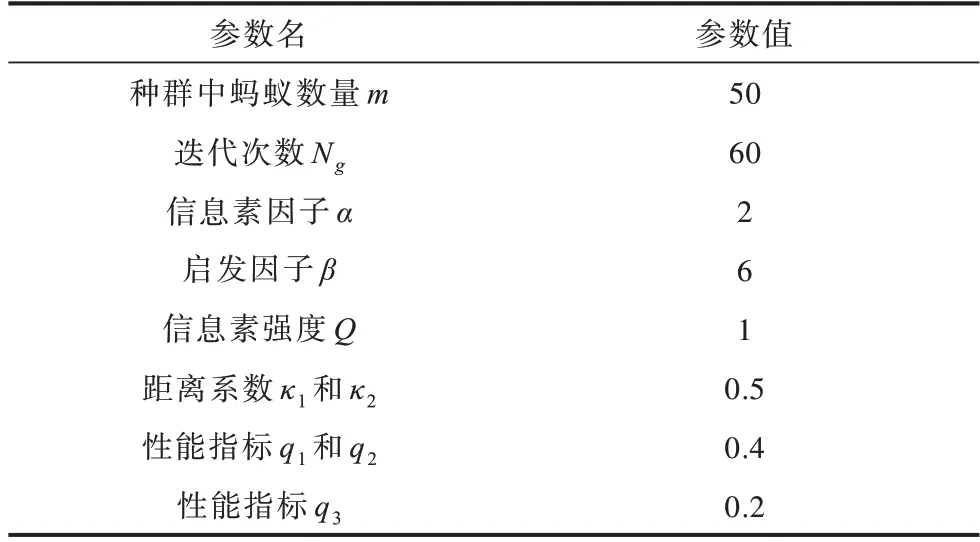
表1 實驗相關參數設置Table 1 Setting of experiment correlation parameters

4.1 非結構化道路場景下的實驗結果與分析

在非結構化道路場景下，為更好地描述動態障礙物在平面地圖中的運動，將時間軸視為運動狀態，使運動狀態沿著各個方向維度離散化，從而將整個場景的變化統一記錄在X-Y-T三維狀態空間中。在規格為20 m×20 m 的地圖中，靜態障礙物所在的位置不隨時間變化而移動，動態障礙物隨著時間序列進行移動。設置自動駕駛車輛數量為Nn，障礙物數量為Nobs，為驗證本文方法的有效性，在兩種不同道路場景（Nn=2 和Nobs=3、Nn=4 和Nobs=4）下進行仿真實驗。

設置自動駕駛車輛的起始點為A1，A2，…，An，終點為B1，B2，…，Bn。使用改進的蟻群優化算法進行自動駕駛運動規劃，在兩種場景下所規劃的軌跡分別如圖3、圖4 所示。由圖3、圖4 可知，基于改進蟻群優化算法的自動駕駛協同運動規劃能夠有效規避障礙物，并為各自動駕駛車輛規劃出無碰撞的平滑路線。各種群所代表的自動駕駛車輛在迭代過程中的綜合代價變化曲線如圖5、圖6 所示。由圖5、圖6 可知，隨著迭代次數的增加，綜合代價快速下降，表明改進的蟻群優化算法在迭代初期能夠快速收斂，在經過一定的迭代次數后，綜合代價逐漸趨于穩定，最終收斂于特定值。

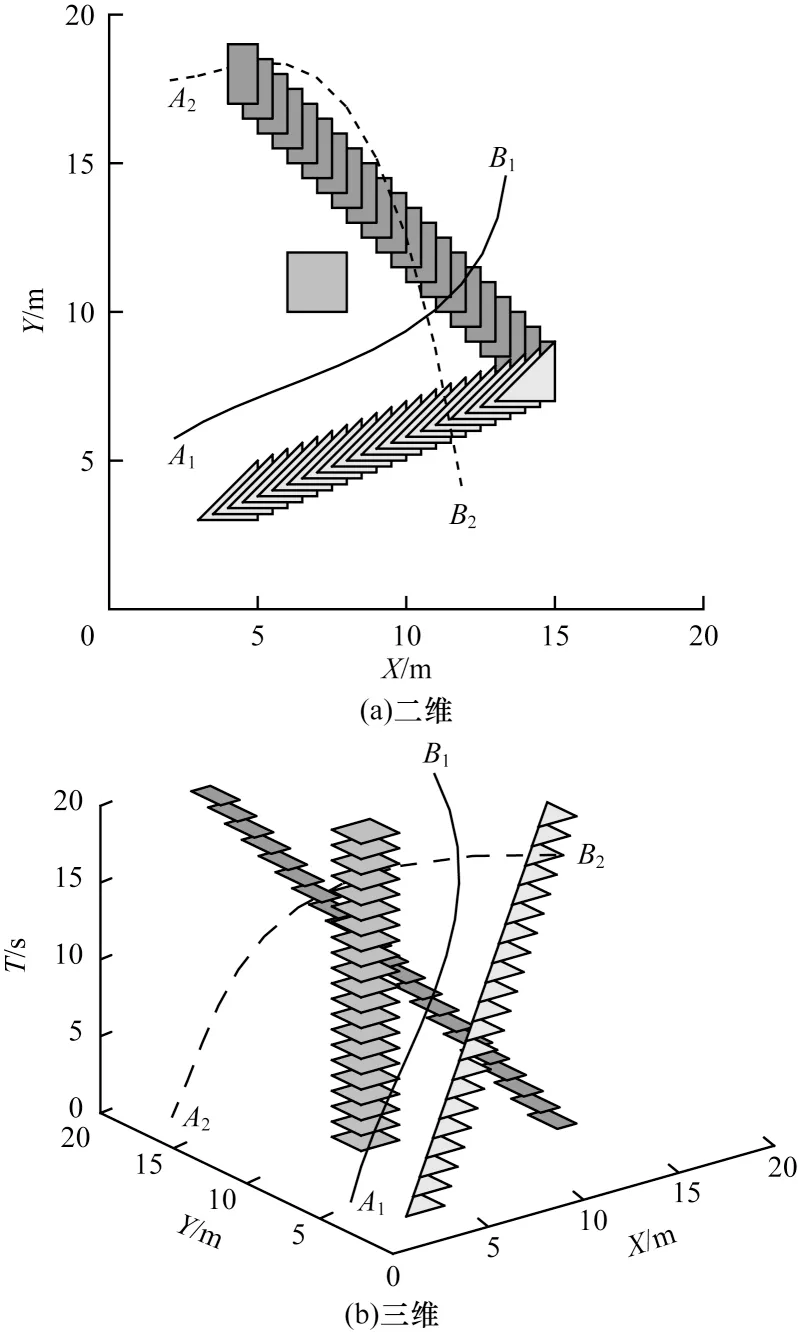
圖3 Nn=2 和Nobs=3 條件下協同運動規劃結果Fig.3 Results of collaborative motion planning under the conditions of Nn=2 and Nobs=3

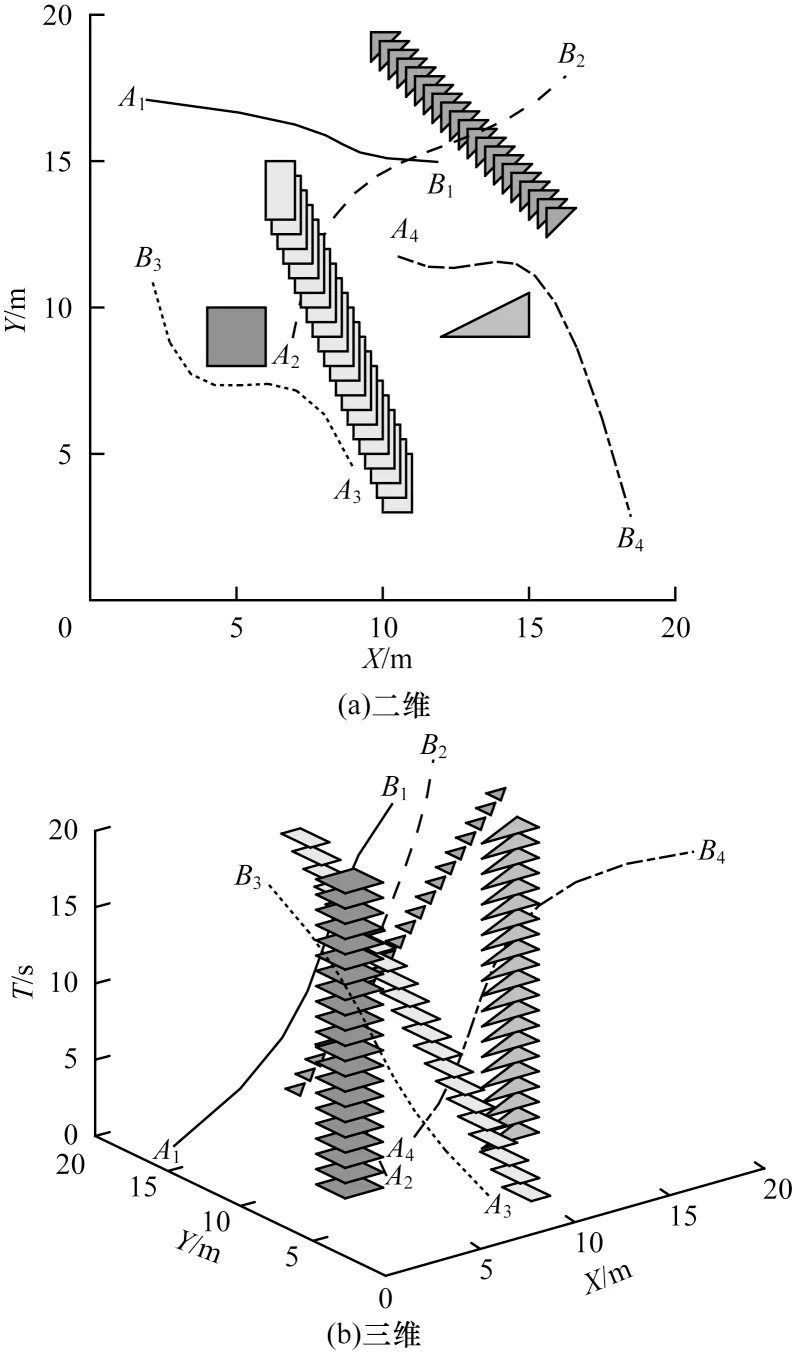
圖4 Nn=4 和Nobs=4 條件下協同運動規劃結果Fig.4 Results of collaborative motion planning under the conditions of Nn=4 and Nobs=4

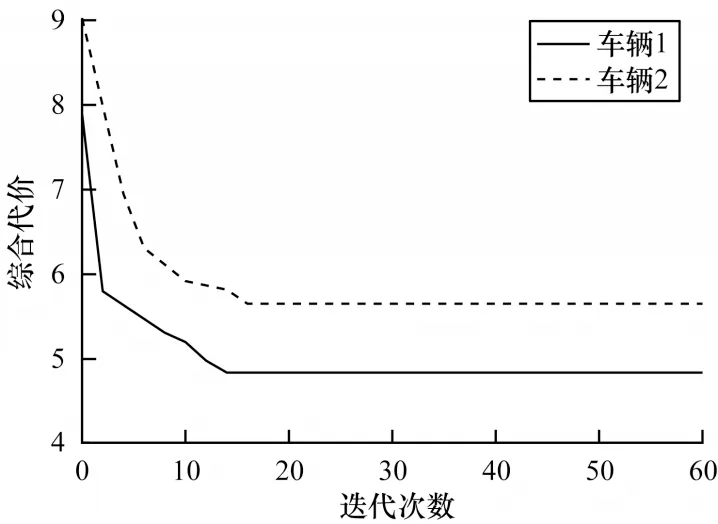
圖5 Nn=2 和Nobs=3 條件下綜合代價變化曲線Fig.5 Change curves of comprehensive cost under the condition of Nn=2 and Nobs=3

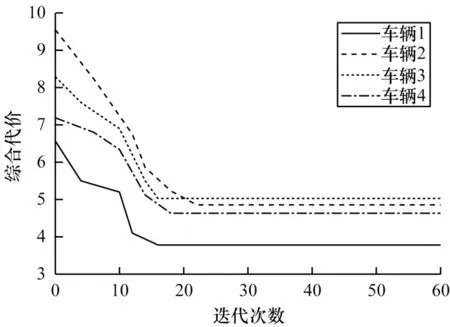
圖6 Nn=4 和Nobs=4 條件下綜合代價變化曲線Fig.6 Change curves of comprehensive cost under the condition of Nn=4 and Nobs=4

4.2 結構化道路場景下的實驗結果與分析

構建簡單結構化道路場景進行仿真實驗，如圖7（a）～圖7（g）所示，3 輛自動駕駛車輛行駛在一條雙車道的直線道路上，設置初始速度v1=v2=v3=20 m/s，各自動駕駛車輛速度可變并根據環境做出適當的控制，以響應動態環境的變化。采用本文方法進行自動駕駛協同運動規劃，仿真結果如圖7（h）所示。在圖7 中，實線、虛線以及點劃線分別表示車輛1、車輛2、車輛3 的規劃路線，所生成的軌跡平滑，且各車輛之間保持協同控制并滿足約束條件。

圖7 結構化道路場景下的協同運動規劃結果Fig.7 Result of collaborative motion planning under the scene of structured road

在模擬過程中，當T=0 s 時，各自動駕駛車輛分別位于0 m、40 m 以及80 m 處；當T=4 s 時，車輛2 繼續保持v2=20 m/s 的速度向前行駛，此時車輛1 由于速度的增加，距離車輛2 越來越近，為避免發生事故，車輛1 采取變道措施；當T=8 s 時，車輛1 完成變道，避免了與車輛2 發生碰撞；當T=16 s 時，由于車輛3 以低于車輛1 的速度前進，阻礙了車輛1 的行駛，車輛1 在保持安全的前提下繼續變道；當T=20 s時，由于車輛1 的變道，車輛2 若繼續保持勻速行駛，距離車輛1 過近，存在安全隱患，為確保行車安全，采取減速措施；當T=24 s 時，車輛1 完成變道。

結構化道路場景中各自動駕駛車輛的綜合代價曲線如圖8 所示，在迭代初期，代價曲線的值快速下降，表明經過迭代次數的增加，各種群已能規劃出較優軌跡。在后續迭代過程中，綜合代價逐漸達到穩定值。在仿真過程中，各車輛速度及加速度的變化如圖9（a）和圖9（b）所示，各自動駕駛車輛的速度根據動態環境做出自適應調整。

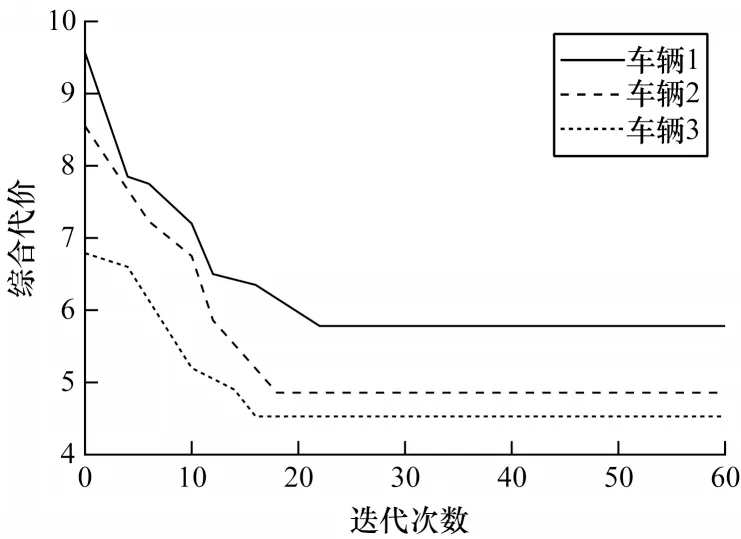
圖8 結構化道路場景下的綜合代價變化曲線Fig.8 Change curves of comprehensive cost under the scene of structured road

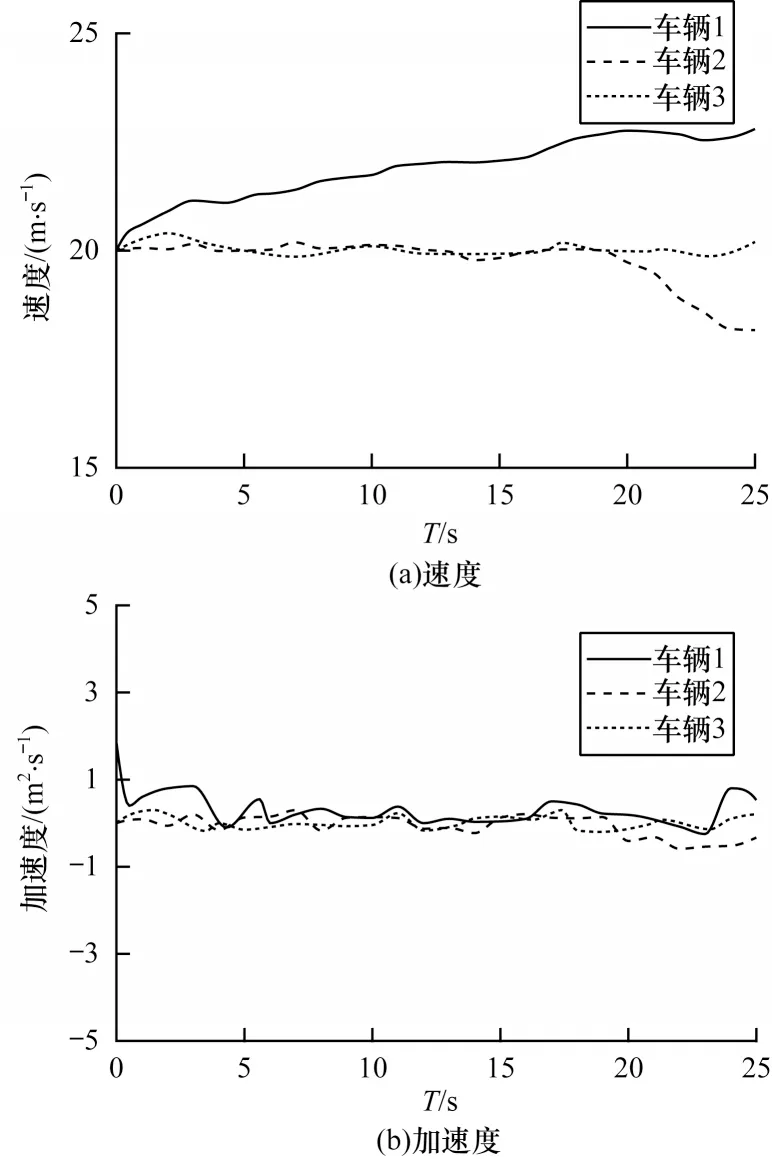
圖9 車輛參數變化Fig.9 Changes of vehicle parameters

4.3 性能對比

為驗證本文方法性能，將其與APF 方法［12］進行對比。在相同參數設置條件下，通過代價函數對比協同收斂性能，分別記錄第i次迭代得到的代價函數均值Ji與初次迭代得到的代價函數均值Jo，并用Ji/Jo表示算法收斂速度。兩種方法在不同車輛數量情況下的收斂曲線如圖10 和圖11 所示，可以看出本文方法收斂速度明顯優于APF 方法，且所得解的適應性更強，在復雜道路場景下，隨著自動駕駛車輛數量增多，代價函數均值比減小，且收斂于更小的值，表明車輛間協同效果更好。

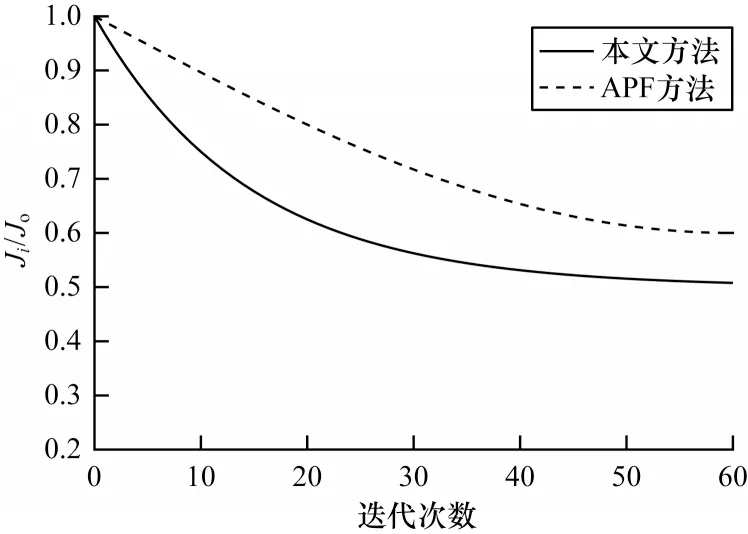
圖10 Nn=3 時2 種方法的收斂曲線Fig.10 Convergence curves for two methods when Nn=3

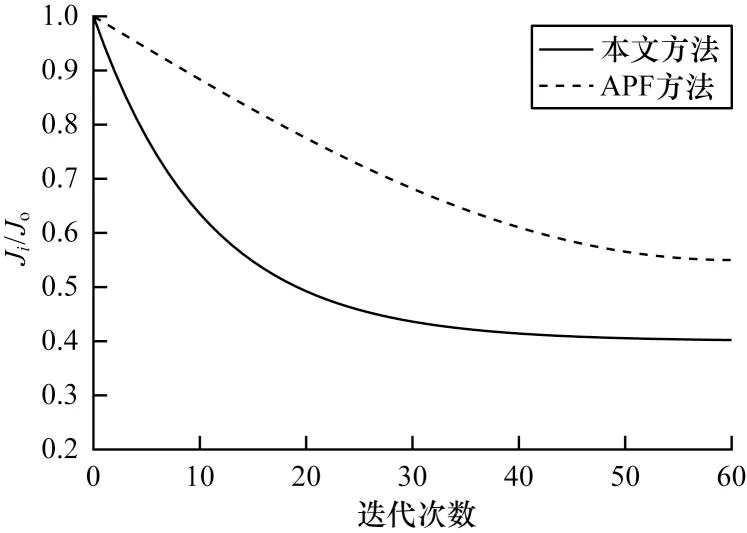
圖11 Nn=6 時2 種方法的收斂曲線Fig.11 Convergence curves for two methods when Nn=6

5 結束語

本文針對復雜道路場景下的自動駕駛多車運動規劃問題，提出一種基于改進蟻群優化算法的協同控制方法。在蟻群優化算法的信息素更新過程中，引入以空間協同和軌跡代價為目標函數的多目標優化模型，使各自動駕駛車輛保持協同控制，同時對蟻群優化算法的揮發因子進行自適應調整，加快算法收斂速度。實驗結果表明，該方法為多輛自動駕駛汽車的協同運動規劃提供了一種有效的解決方案。后續將設計協同控制器，對多輛自動駕駛汽車的規劃路線進行跟蹤控制，并將本文方法應用于實際自動駕駛系統，進一步提升其穩定性。