變參數(shù)線性跟蹤微分器及其在地平式大視場望遠(yuǎn)鏡中的應(yīng)用

楊曉霞，鄧永停，趙金宇，張 斌

（中國科學(xué)院 長春光學(xué)精密機(jī)械與物理研究所，吉林 長春 130033）

1 引 言

自抗擾控制方法（Active Disturbance Rejection Control，ADRC［1-2］）是一種基于過程誤差來抑制或消除誤差的控制方法，在工業(yè)和工程領(lǐng)域得到了廣泛的應(yīng)用［3-8］。跟蹤微分器（Tracking Differentiator，TD［9］）是自抗擾控制方法的一個(gè)主要組成部分，主要用于對不連續(xù)或帶隨機(jī)噪聲的信號提取連續(xù)信號及微分信號。大量的理論研究工作針對TD 的收斂性［10-11］、微分信號的提取能力以及濾波能力［12-14］展開，很多TD 的改進(jìn)形式［15-16］被提出并應(yīng)用在不同領(lǐng)域中［17-18］。事實(shí)上，TD 的一個(gè)主要作用是用于對控制系統(tǒng)中的參考信號進(jìn)行過渡過程安排，過渡過程信號作為參考信號和反饋信號之間的一個(gè)橋梁，當(dāng)參考信號發(fā)生大的跳變時(shí)，仍然能夠保證反饋信號跟蹤一個(gè)連續(xù)漸變的過渡過程信號，從而使得控制誤差不會(huì)出現(xiàn)大的跳變，進(jìn)而保證控制系統(tǒng)的穩(wěn)定性和魯棒性。

TD 又分為線性TD（Linear TD，LTD）和非線性TD（Nonlinear TD，NLTD）。在安排過渡過程時(shí)，LTD 的優(yōu)點(diǎn)在于算法復(fù)雜度低，簡單易實(shí)現(xiàn)，缺點(diǎn)在于跟蹤不同幅值的階躍信號時(shí)，需要調(diào)節(jié)快速因子參數(shù)，否則容易造成LTD 輸出信號的速度和加速度過大或者過小，起不到過渡作用。NLTD 的優(yōu)點(diǎn)在于通過使用最速控制綜合函數(shù)，使得在一定加速度的限制下能夠最快地跟蹤參考輸入，但是其算法復(fù)雜度高、計(jì)算量大，并且在跟蹤不同幅值的階躍信號時(shí)也存在輸出速度過大或過小的問題。

在使用跟蹤微分器安排過渡過程時(shí)，應(yīng)該使得輸出的過渡過程信號的速度、加速度與物理系統(tǒng)的反饋能力相匹配，否則，過渡過程信號變化太快起不到過渡作用，變化太慢會(huì)影響系統(tǒng)的最大跟蹤能力。本文研究了一種帶速度和加速度飽和限制的變參數(shù)線性跟蹤微分器，它既能夠在參考信號和反饋信號之間起過渡橋梁的作用，又能夠充分發(fā)揮受控物理對象的最大速度和最大加速度能力。

2 TD 性能分析

經(jīng)典的安排過渡過程的工具是LTD 和NLTD。

2.1 線性跟蹤微分器

LTD 的離散形式如下：

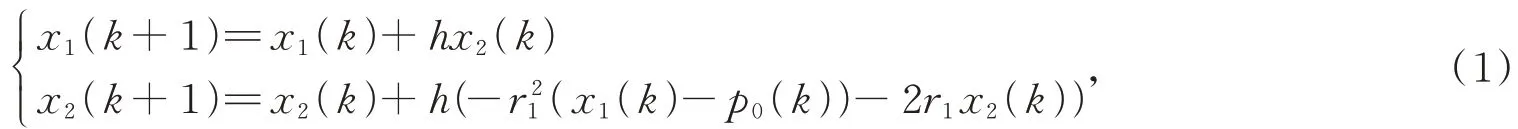
其中：p0為設(shè)定值，h是離散化的采樣步長參數(shù)，r1為快速因子，是系統(tǒng)唯一的可調(diào)參數(shù)，它決定系統(tǒng)的收斂速度。當(dāng)設(shè)定值p0(k)≡p0為常值時(shí)，定義x1第一次到達(dá)0.99p0的時(shí)間為過渡時(shí)間T0，定義VmaxLTD和amaxLTD分別是LTD 輸出的最大速度和最大加速度，也就是VmaxLTD=max(|x2|)，amaxLTD=max(|x?2|)，表1給出了LTD 的最大速度和最大加速度與參數(shù)和設(shè)定值之間的關(guān)系。

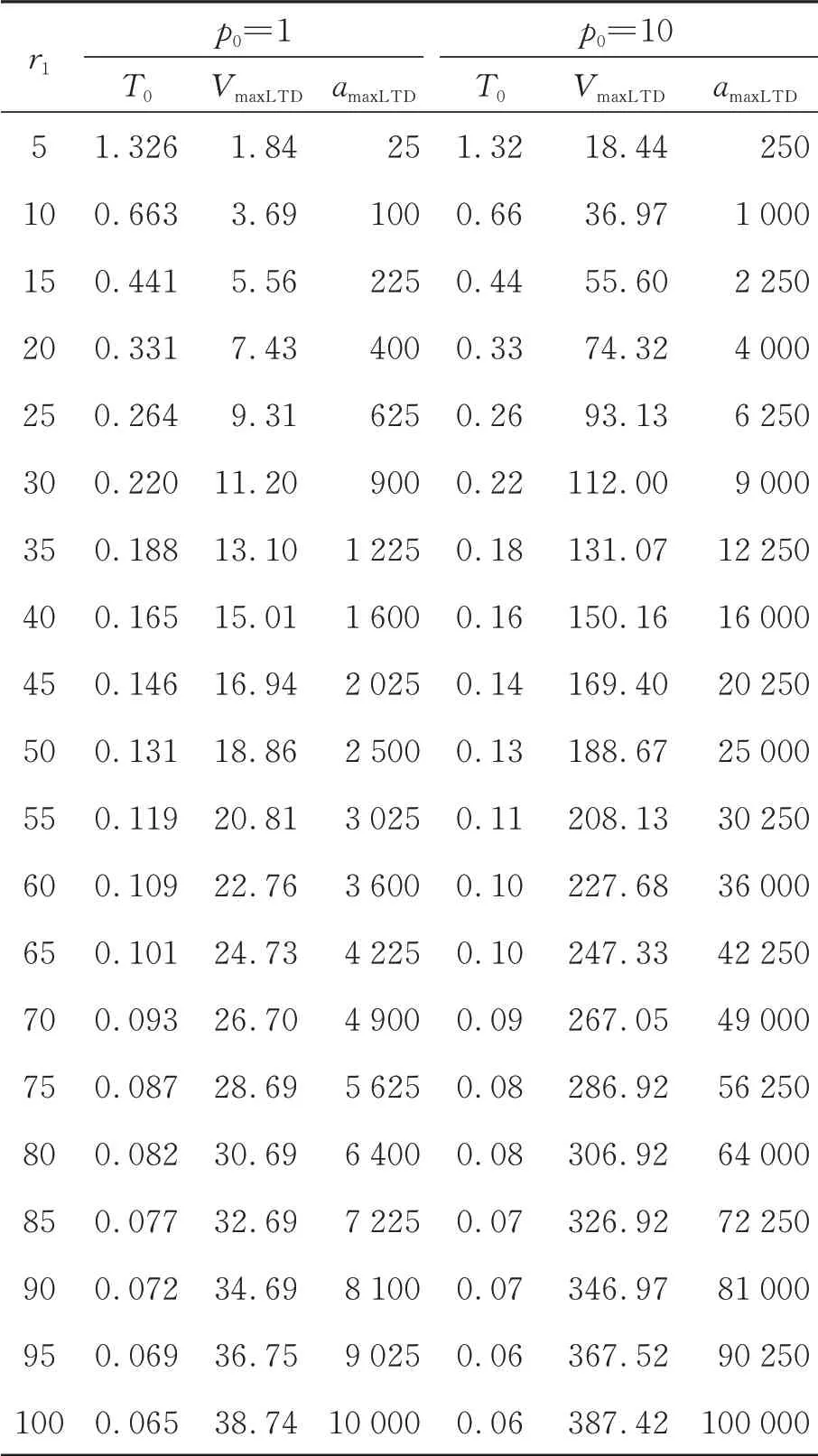
表1 LTD 的最大速度和最大加速度與參數(shù)的對應(yīng)關(guān)系Tab.1 Relationship among VmaxLTD，amaxLTD and parameters

使用MATLAB 的數(shù)據(jù)擬合工具，可以得到擬合表達(dá)式：

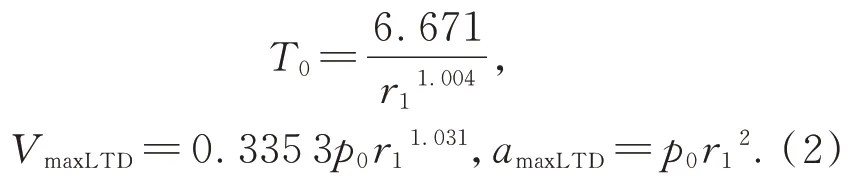
圖1 給出了當(dāng)p0=1 時(shí)離散計(jì)算結(jié)果與擬合函數(shù)曲線之間的關(guān)系。可以看出，過渡過程時(shí)間T0與參數(shù)r1成反比，并且與最終的穩(wěn)態(tài)響應(yīng)值沒有關(guān)系，這說明使用LTD 安排過渡過程時(shí)，只要參數(shù)r1確定，跟蹤穩(wěn)態(tài)值1 和跟蹤穩(wěn)態(tài)值100 或者10 000 的時(shí)間是相同的，這就導(dǎo)致LTD 給出的VmaxLTD和amaxLTD均與穩(wěn)態(tài)值p0相關(guān)，p0越大，VmaxLTD和amaxLTD越大，而如果VmaxLTD和amaxLTD遠(yuǎn)遠(yuǎn)超過物理系統(tǒng)的反饋速度和加速度能力，那么物理系統(tǒng)的反饋信號就無法跟蹤LTD 所給出的過渡過程信號，此時(shí)LTD 所給出的信號就起不到過渡作用。

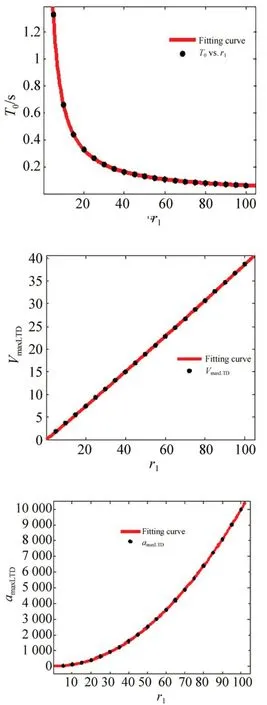
圖1 T0，VmaxLTD，amaxLTD 與LTD 參數(shù)r1的關(guān)系Fig.1 Relationship between T0，VmaxLTD，amaxLTD and r1

另一方面，通過簡單地在LTD 的輸出信號上加入速度和加速度飽和環(huán)節(jié)，是不能夠解決這個(gè)問題的，因?yàn)橥ㄟ^仿真計(jì)算可以看出，此時(shí)LTD 的輸出會(huì)發(fā)生振蕩。設(shè)p0=100，r1=15，h=0.001，根據(jù)式（2）可以推算出LTD 給出的最大速度和最大加速度如下：

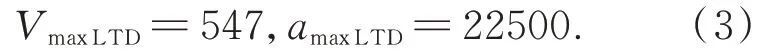
設(shè)物理系統(tǒng)反饋的最大速度Vmax和最大加速度amax如下：

圖2 給出了加入式（4）的速度和加速度上界后LTD 的輸出曲線。

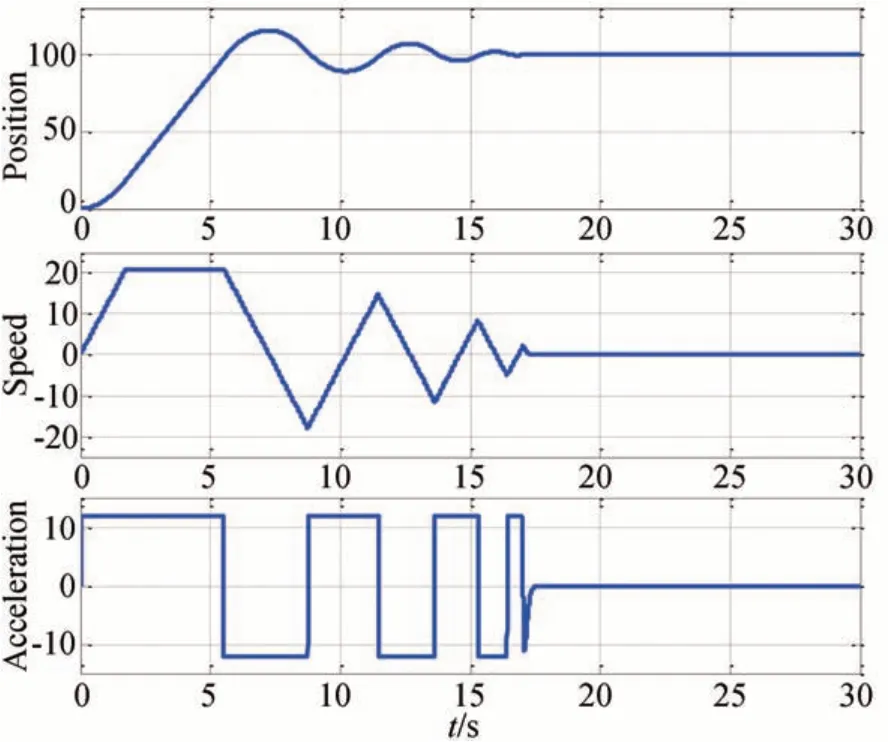
圖2 帶速度和加速度飽和限制的LTD 輸出Fig.2 Output of LTD with speed and acceleration saturation

2.2 非線性跟蹤微分器

離散最速跟蹤微分器利用fhan 函數(shù)實(shí)現(xiàn)，它的加速度通過參數(shù)r限定，具體形式如下：

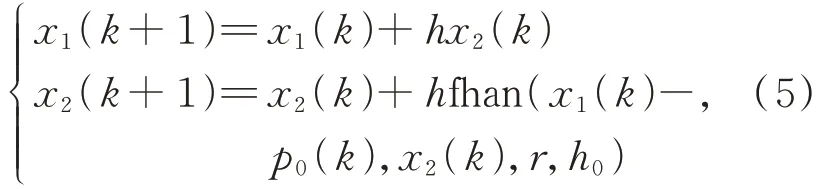
其中：h是采樣周期，r是快速因子，h0是濾波因子，可以大于采樣周期h，fhan 是非線性函數(shù)，具體形式如下：

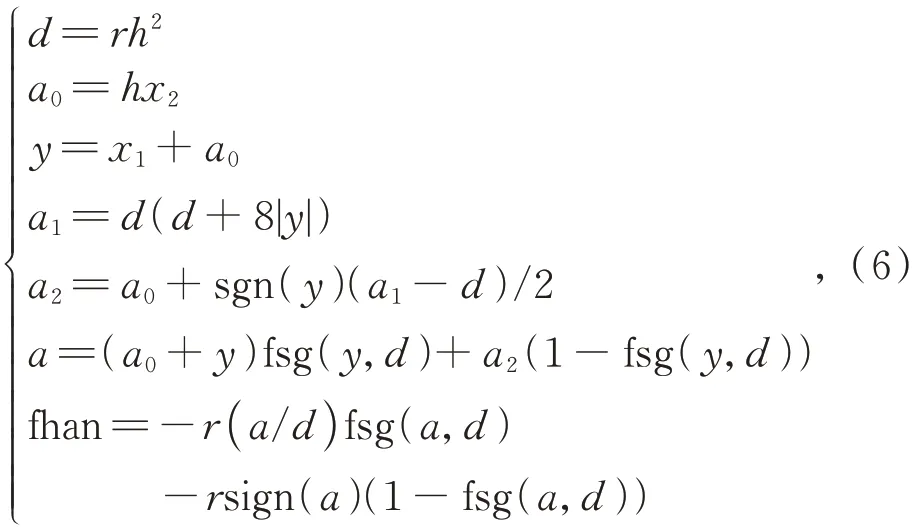
其中：fsg(a，d)=(sgn(x+d)-sgn(x-d))/2，sgn(·)是符號函數(shù)。經(jīng)過計(jì)算可以得到T0，VmaxN-LTD以及amaxNLTD與參數(shù)r和p0的關(guān)系如下：

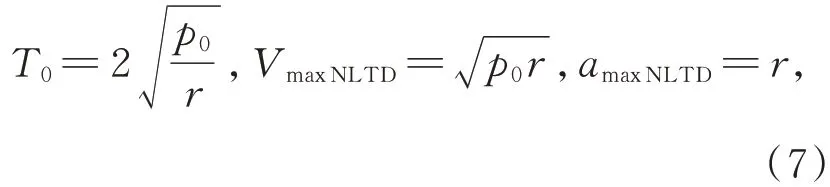
其中VmaxNLTD和amaxNLTD分別是NLTD 的最大速度和最大加速度。可以看出，NLTD 的加速度是具有上限的，但是最大速度跟穩(wěn)態(tài)值p0有關(guān)，沒有上限，因此帶有速度飽和Vmax的NLTD 設(shè)計(jì)如下：

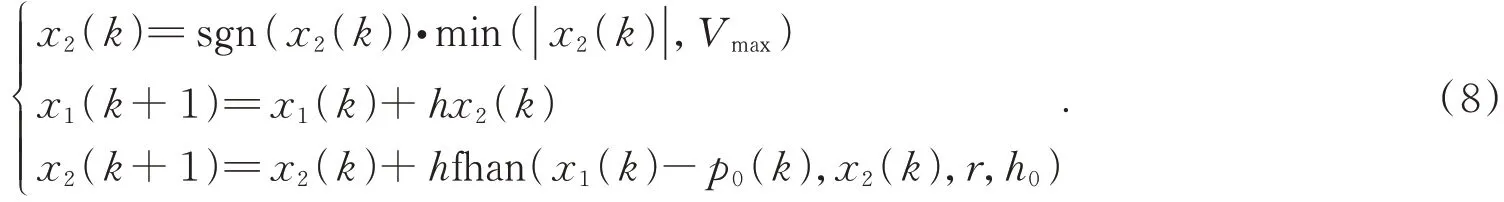
與LTD 不同，給NLTD 加入速度飽和限制之后不會(huì)引起信號的波動(dòng)。圖3 給出了帶有速度飽和的NLTD 輸出曲線，其中p0=100，Vmax=21，r=12，h=0.001，h0=0.01。

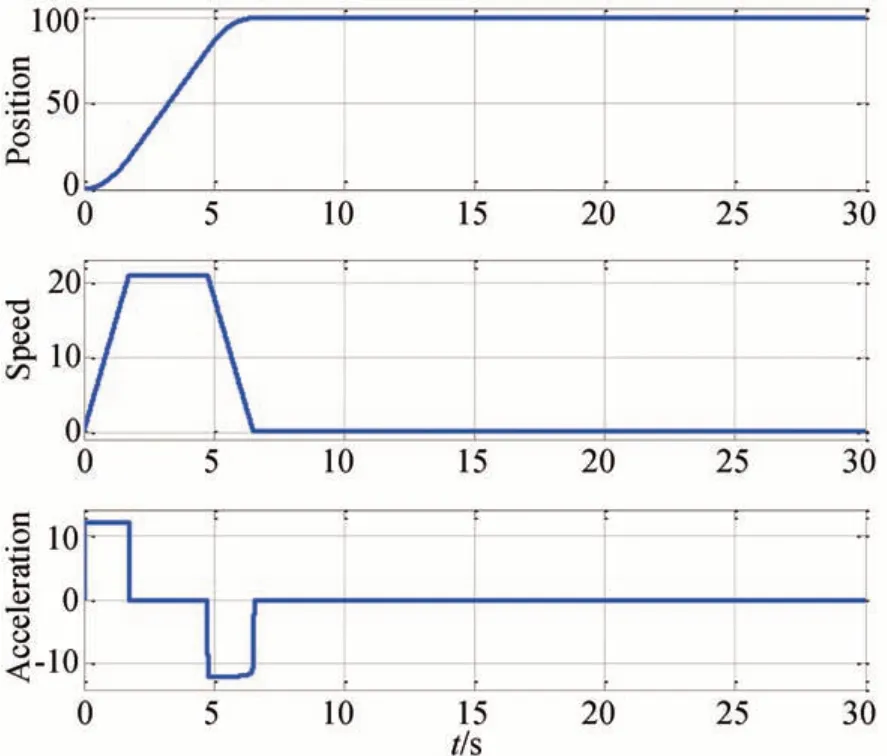
圖3 帶速度飽和的NLTD 輸出Fig.3 Output of NLTD with speed saturation

帶有速度飽和的NLTD 可以給出與物理系統(tǒng)反饋能力相匹配的過渡過程信號，在實(shí)現(xiàn)過渡作用的同時(shí)能夠充分發(fā)揮系統(tǒng)的最大反饋能力。但是，由于非線性函數(shù)fhan 的計(jì)算比較復(fù)雜，不利于在工程中的實(shí)時(shí)實(shí)現(xiàn)。本文給出一種變參數(shù)LTD，合理地將參數(shù)r設(shè)計(jì)為跟蹤誤差的函數(shù)，克服了LTD 的不足，并且比帶有速度飽和的NLTD 更簡單易實(shí)現(xiàn)。

3 變參數(shù)線性跟蹤微分器設(shè)計(jì)

連續(xù)的VLTD 設(shè)計(jì)如下：

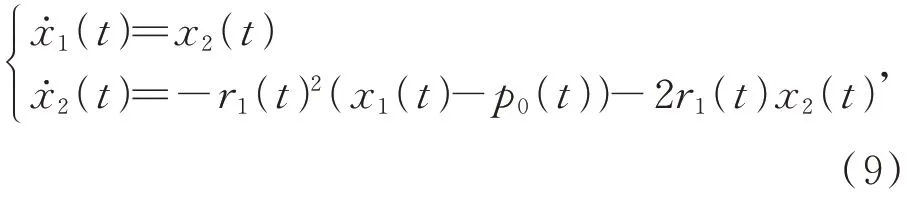
其中時(shí)變參數(shù)r1（t）設(shè)計(jì)如下：

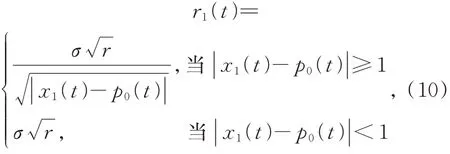
其中：r可以設(shè)計(jì)為反饋物理信號的最大加速度，σ≥1 是唯一的可調(diào)參數(shù)。將式（10）代入式（9）可以得到VLTD 的一般形式如下：

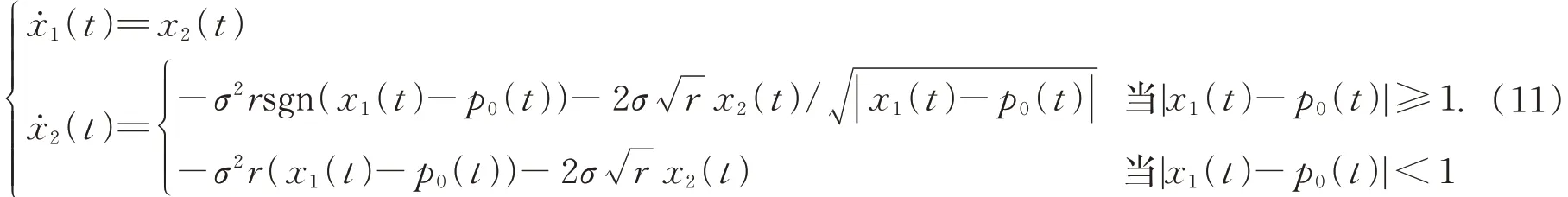
可以看出，VLTD 與LTD 的區(qū)別在于將快速因子設(shè)置為一個(gè)時(shí)變函數(shù)，它設(shè)計(jì)為跟蹤誤差的減函數(shù)，以此保證初期跟蹤誤差非常大時(shí)，過渡過程的加速度也不會(huì)非常大。當(dāng)跟蹤誤差小于1 時(shí)，VLTD 就變?yōu)長TD。

3.1 VLTD 的收斂性分析

對VLTD 的收斂性進(jìn)行分析，得到如下定理。

定理1，設(shè)p0是常值，對于任意的初值x1（0）和x2（0）=0，VLTD 都能在有限時(shí)間內(nèi)收斂至線性區(qū)間內(nèi)，其中線性區(qū)間定義為跟蹤誤差的絕對值小于1 的區(qū)間。

證 明：設(shè)z1(t)=x1(t)-p0，z2(t)=x2(t)，σr=σ，那么VLTD 可以簡化為：

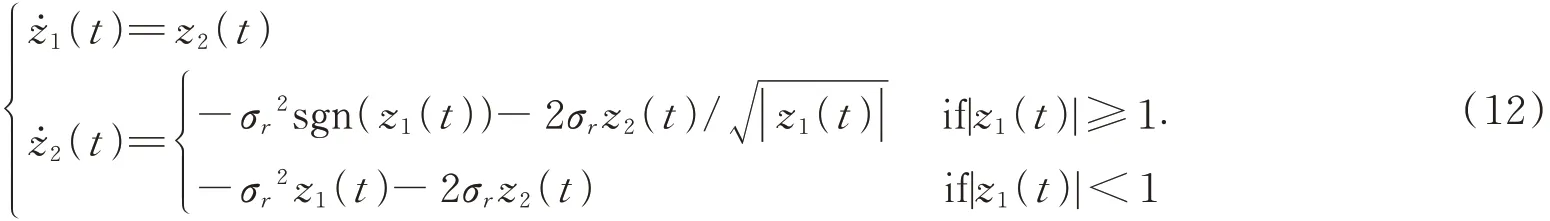
因此只需證明對于任意的z1(0) 和z2(0)=0，存在時(shí)間點(diǎn)tc＞0 使得|z1(tc)|＜1。

情形1：如果|z1(0)|＜1，那么當(dāng)t＞0 時(shí)系統(tǒng)的變化規(guī)律如下：

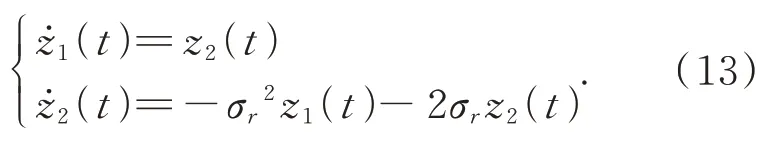
上述微分方程的解如下：

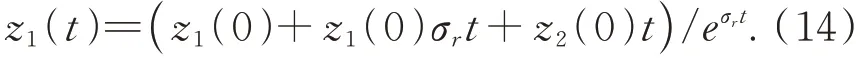
由于z2(0)=0，所以有：

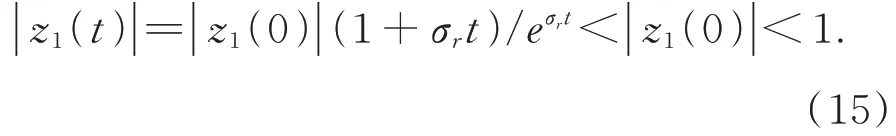
對于情形1，當(dāng)系統(tǒng)的初值處于線性區(qū)間時(shí)，系統(tǒng)始終處于線性區(qū)間內(nèi)。

情形2：如果z1(0)≥1，那么系統(tǒng)的變化規(guī)律如下：

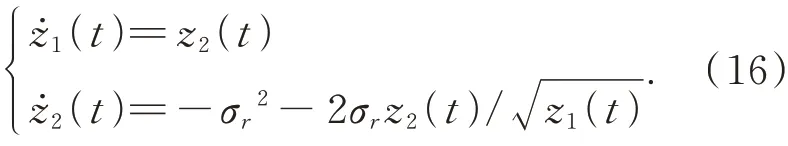
整理第二個(gè)方程得到：

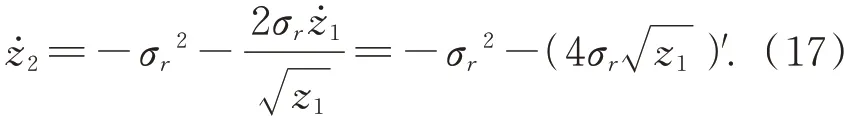
在時(shí)間區(qū)間[0，τ]上對等式兩邊進(jìn)行積分，得到：

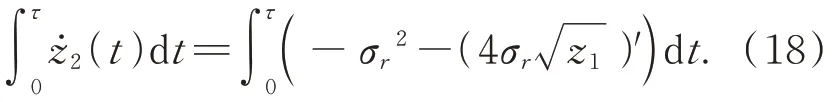
進(jìn)一步整理得：

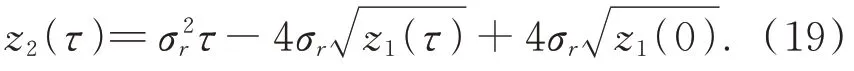
將式（19）在時(shí)間區(qū)間[0，t]上進(jìn)行積分，得到：

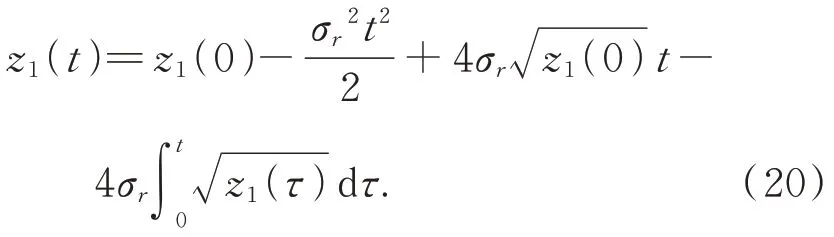
如果存在時(shí)間點(diǎn)tc∈[0，t]，使得z1(tc)＜1，那么結(jié)論成立。而如果對于任意的τ∈[0，t]都有z1(τ)≥1，那么：

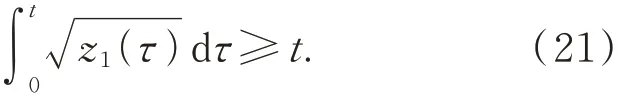
整理式（21）得：

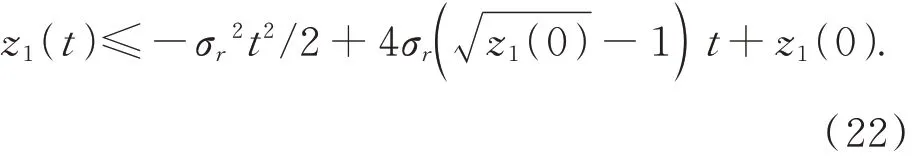
顯然，不等式的右邊是關(guān)于t的二次函數(shù)，當(dāng)t＞4(-1)/σr時(shí)，式（22）的右邊相對于t是一個(gè)單調(diào)遞減函數(shù)，并且：

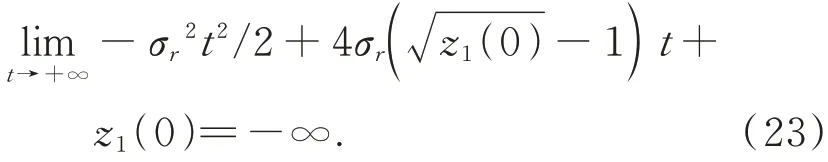
因此，一定存在tc＞0，使得：

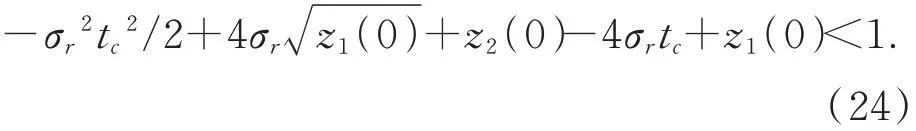
從而有：

結(jié)論成立。

情形3：如果z1(0)≤-1，那么系統(tǒng)的變化規(guī)律如下：

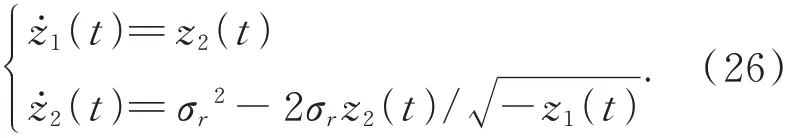
整理第二個(gè)方程可得：

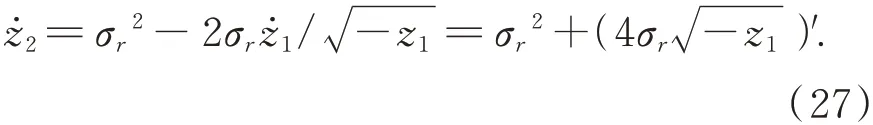
將 式（27）的 兩 端 在 時(shí) 間 區(qū) 間[0，τ] 上 積分得：

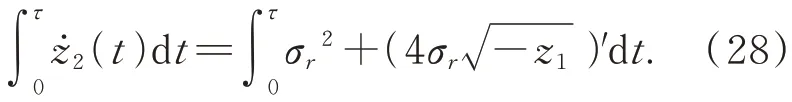
進(jìn)一步整理得：

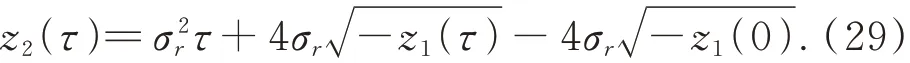
將上述方程的兩邊在時(shí)間區(qū)間[0，t]上積分得：

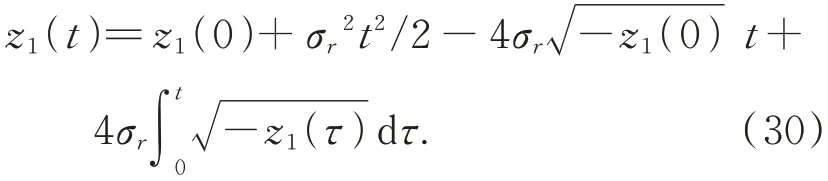
如果存在tc∈[0，t]，使得z1(tc)＞-1，那么結(jié) 論 成 立。如 果 對 于 任 意 的?τ∈[0，t]都 有z1(τ)≤-1，那么有：

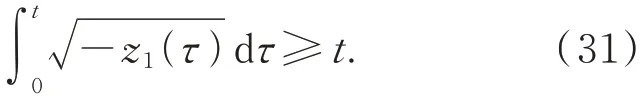
因此有：

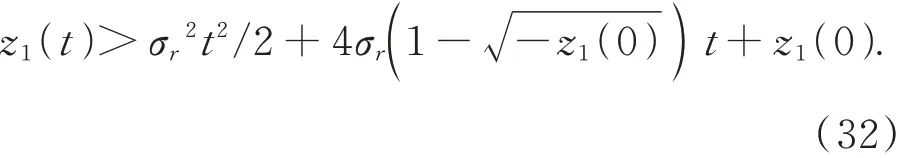
顯然，不等式右邊是一個(gè)關(guān)于t的二次函數(shù)，當(dāng)t＞時(shí)，不 等 式 右 邊 是 一個(gè)關(guān)于t的單調(diào)遞增函數(shù)，并且有：

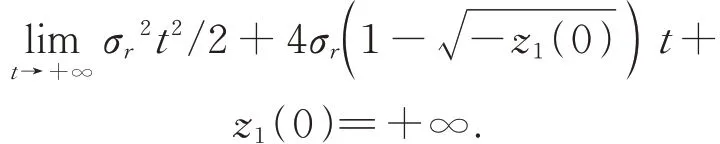
所以存在tc＞0，使得：

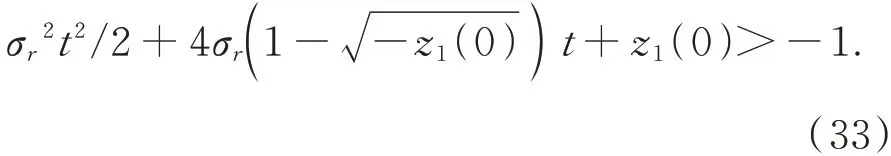
因此有：

定理結(jié)論成立。

上述結(jié)論說明，對于任意的初值x1（0），VLTD 必定能在有限時(shí)間內(nèi)收斂至線性區(qū)間內(nèi)。

3.2 VLTD 的速度和加速度上限分析

設(shè)tvmax為VLTD 到達(dá)速度上限的時(shí)間點(diǎn)，那么有x?2(tvmax)=0，也就是：

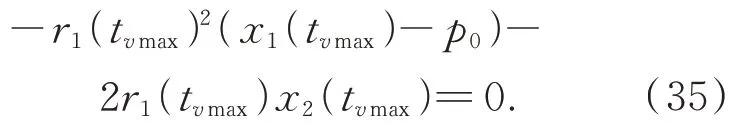
進(jìn)一步整理得：

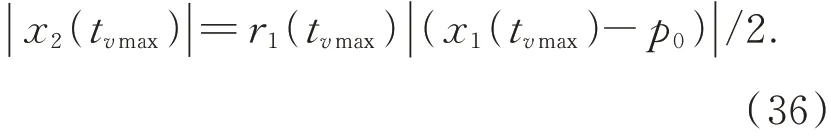
如果|x1(tvmax)-p0|＜1，那么有：

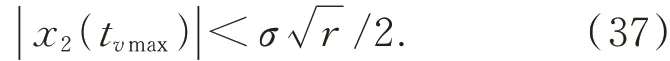
如果|x1(tvmax)-p0|≥1，那么有：

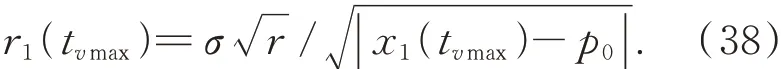
也就是：

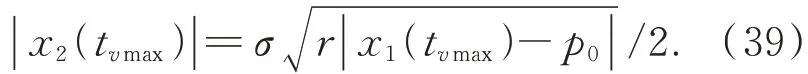
根據(jù)VLTD 的特點(diǎn)，|x1(tvmax)-p0|≥p0/2，因此VLTD 的最大速度滿足：

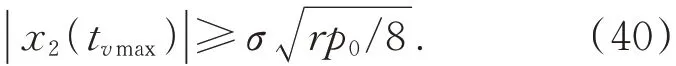
不等式（40）說明當(dāng)|x1(tvmax)-p0|≥1 時(shí)，VLTD 的速度輸出最大值不存在上限。

另一方面，可以推導(dǎo)出VLTD 在初始時(shí)刻達(dá)到最大加速度σ2r，并且減速階段的加速度明顯比加速階段的加速度小。為了避免VLTD 減速階段的加速度過小，一般選取參數(shù)σ＞1，這樣就會(huì)導(dǎo)致加速階段的加速度會(huì)超過物理系統(tǒng)的最大反饋加速度，因此，在VLTD 的加速度輸出上加入加速度飽和上限即可。

通過上面的分析可知，有必要對VLTD 的速度和加速度輸出加入飽和限制，記x3為VLTD 的加速度輸出，VmaxVLTD為VLTD 的速度上限，那么帶有速度和加速度飽和限制的離散VLTD 形式設(shè)計(jì)如下：

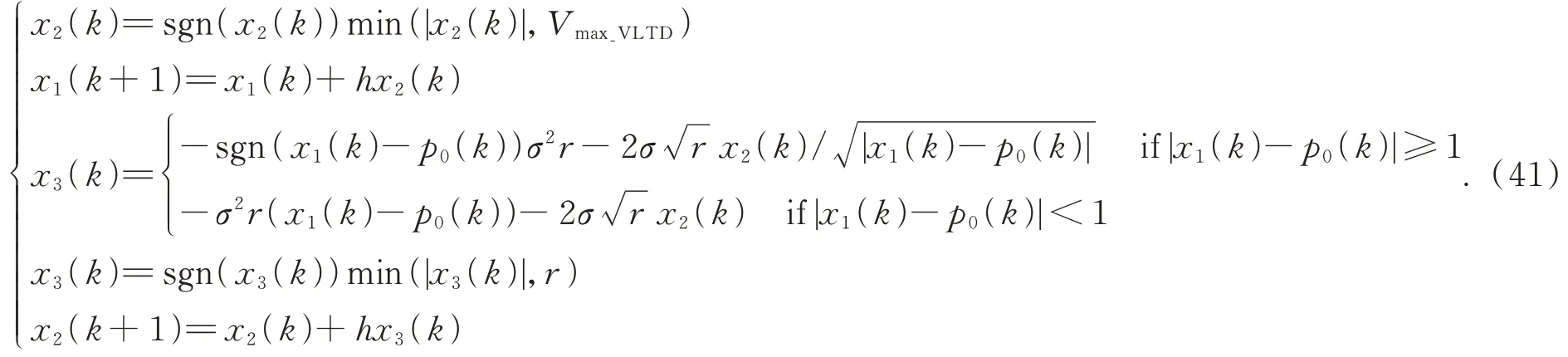
3.3 仿真設(shè)計(jì)

設(shè)物理系統(tǒng)的最大速度和最大加速度分別為Vmax=20 和amax=12，VLTD 的參數(shù)取值如下：采 樣 步 長h=0.001，σ=2.3，r=12，速 度 上 限VmaxVLTD=20，加速度上限為r，穩(wěn)態(tài)響應(yīng)值p0=100，50，10，1，圖4 分別給出了加入速度和加速度限制前后的VLTD 輸出對比曲線。可以看出，加入速度和加速度飽和限制之后，VLTD 的收斂性沒有受到影響，而且在p0較大，也就是VLTD 本身輸出的最大速度超過VmaxVLTD時(shí)，速度飽和才起作用；而在p0較小時(shí)，也就是VLTD 本身輸出的最大速度不超過VmaxVLTD時(shí)，速度飽和不起作用。一旦σ確定之后，無論p0取值如何，加速度飽和都會(huì)起作用，因?yàn)橹灰遥?，那么初始段的加速度一定會(huì)大于r。

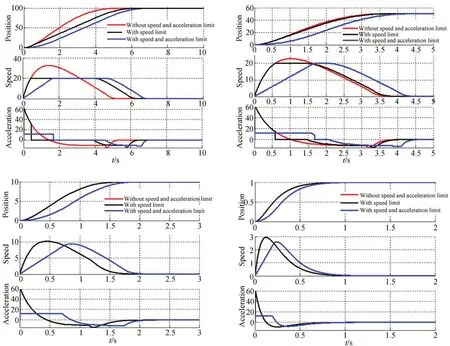
圖4 速度及加速度飽和對VLTD 輸出的影響Fig.4 Impact of speed and acceleration saturation on output of VLTD

將帶速度和加速度飽和的VLTD（41）與帶速度飽和的NLTD（7）進(jìn)行比較，其中VLTD 的參數(shù)取值與上面仿真相同，NLTD 的參數(shù)取值為r=12，h0=0.01，穩(wěn)態(tài)值p0取為100，圖5 給出了兩者的對比曲線。可以看出，VLTD 可以達(dá)到與NLTD 幾乎相同的效果，并且從加速度曲線上可以看出，在接近穩(wěn)態(tài)值時(shí)，VLTD 的加速度曲線更平滑，這有利于反饋信號的平穩(wěn)快速地跟蹤。另外，VLTD 的計(jì)算復(fù)雜度遠(yuǎn)遠(yuǎn)小于NLTD，在使用時(shí)能夠節(jié)省計(jì)算內(nèi)存空間，有利于算法的實(shí)時(shí)性。

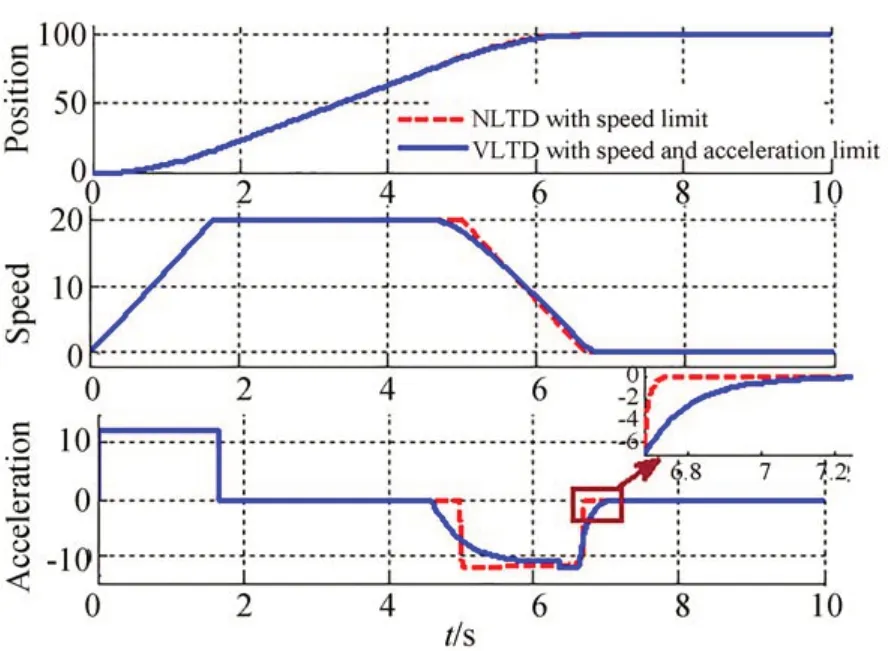
圖5 VLTD 和NLTD 輸出曲線的對比Fig.5 Comparison of output between VLTD and NLTD

4 VLTD 在地平式大視場望遠(yuǎn)鏡中的應(yīng)用

4.1 地平式大視場望遠(yuǎn)鏡搜索路徑分析

大視場望遠(yuǎn)鏡主要針對地球同步軌道（GEO）、同步轉(zhuǎn)移軌道（GTO）及中高軌（MEO）的目標(biāo)進(jìn)行搜索、捕獲、跟蹤和測量。不同軌道的目標(biāo)特性不同，相應(yīng)的工作模式有所不同。由于極軸式望遠(yuǎn)鏡受結(jié)構(gòu)設(shè)計(jì)的限制，望遠(yuǎn)鏡口徑不宜過大，因此將米級大視場望遠(yuǎn)鏡設(shè)計(jì)為地平式結(jié)構(gòu)。由于地平式望遠(yuǎn)鏡方位軸和俯仰軸的耦合作用，無論何種工作模式都會(huì)牽扯到方位軸的頻繁變步長調(diào)轉(zhuǎn)，即使是對固定赤緯的目標(biāo)進(jìn)行搜索。

本文以GEO 目標(biāo)為例進(jìn)行說明，GEO 目標(biāo)的星下點(diǎn)赤緯范圍為±15°，設(shè)觀測站址的經(jīng)緯度為(?s，σs)，A是地平式望遠(yuǎn)鏡的方位角，E是地平式望遠(yuǎn)鏡的俯仰角。以望遠(yuǎn)鏡俯仰角大于10°作為目標(biāo)可觀測的判別條件，可以計(jì)算出觀測站能有效觀測±15°赤緯帶的GEO 目標(biāo)的星下點(diǎn)經(jīng)度為σs±σ0的目標(biāo)，其中σ0由站址緯度?s決定。以兩個(gè)不同緯度的站址為例，設(shè)?s1=24°N，?s2=46°N，望遠(yuǎn)鏡視場為2.5°×2.5°，搜索路徑采取“Z”字型模式，以星下點(diǎn)緯度不變，經(jīng)度以2.5°作為階躍步長，計(jì)算在不同緯度觀測站觀測±15°赤緯帶目標(biāo)時(shí)方位角和俯仰角的變化情況，并且分別計(jì)算了每次調(diào)轉(zhuǎn)時(shí)方位角和俯仰角分別調(diào)轉(zhuǎn)的步長，得到的曲線如圖6 和圖7所示。

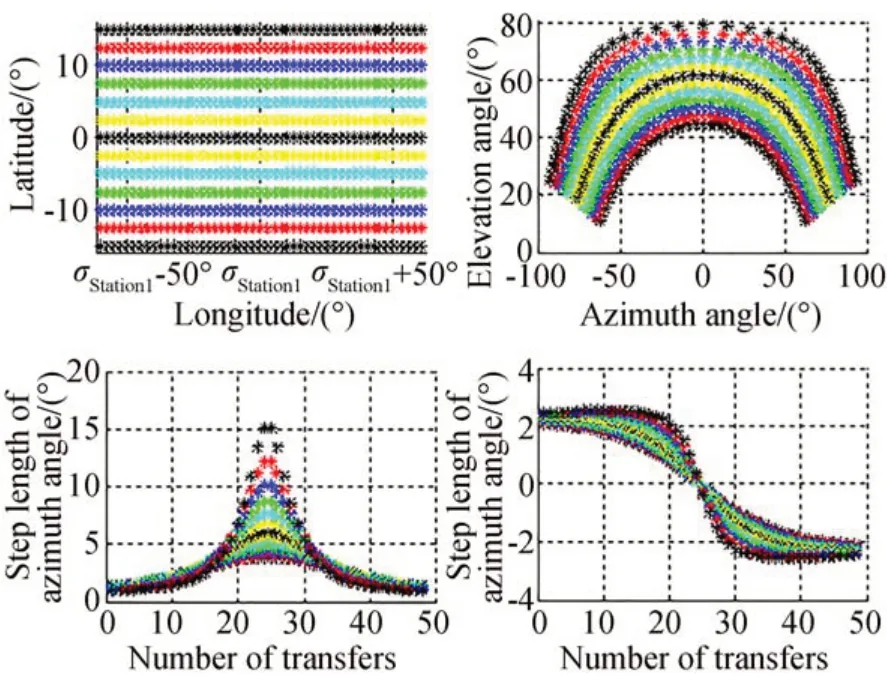
圖6 ?s1=24°N 時(shí)方位角和俯仰角的變化規(guī)律Fig.6 Variation of azimuth and elevation angles with ?s1 of 24°N

對比圖6 和圖7 可以看出，觀測站點(diǎn)緯度越低，觀測GEO 目標(biāo)帶的俯仰角越大，能有效觀測的目標(biāo)帶經(jīng)度范圍就越大，調(diào)轉(zhuǎn)單個(gè)視場時(shí)，方位角需要調(diào)轉(zhuǎn)的步長就越大。對于地平式望遠(yuǎn)鏡來說，即使固定步長掃描同一赤緯的空間目標(biāo)，方位軸仍是進(jìn)行變步長的位置調(diào)轉(zhuǎn)。另外，由于地平式望遠(yuǎn)鏡兩個(gè)軸的耦合運(yùn)動(dòng)，即使掃描同一赤緯的空間目標(biāo)，望遠(yuǎn)鏡的俯仰角并不是固定不變的，而是需要進(jìn)行變步長的位置調(diào)轉(zhuǎn)，上述兩種情況中俯仰軸分別進(jìn)行了0～2°不等的位置調(diào)轉(zhuǎn)。在跟蹤模式下，當(dāng)切換被跟蹤目標(biāo)時(shí)，也需要調(diào)轉(zhuǎn)方位軸和俯仰軸位置，而且調(diào)轉(zhuǎn)的步長與所切換的兩個(gè)目標(biāo)的相對位置有關(guān)。

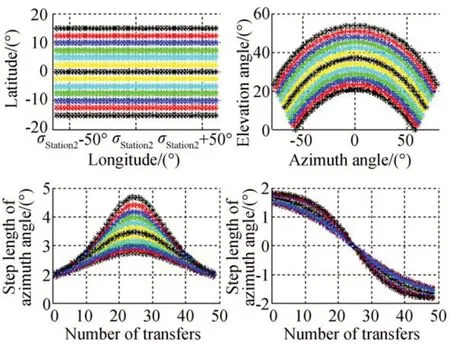
圖7 ?s2=46°N 時(shí)方位角和俯仰角的變化規(guī)律Fig.7 Variation of azimuth and elevation angles with ?s2 of 46°N

4.2 傳統(tǒng)的位置環(huán)分段控制模式

對于地平式大視場望遠(yuǎn)鏡來說，無論是進(jìn)行搜索模式還是跟蹤模式，都會(huì)頻繁涉及到望遠(yuǎn)鏡兩個(gè)軸的變步長位置階躍，而且階躍步長大小不一。傳統(tǒng)的望遠(yuǎn)鏡主軸控制，一般對位置控制環(huán)采用分段控制的方式，當(dāng)位置誤差較大時(shí)，位置環(huán)輸出常值；當(dāng)位置誤差較小時(shí)，則進(jìn)行閉環(huán)解算。位置環(huán)輸出的具體形式如下：

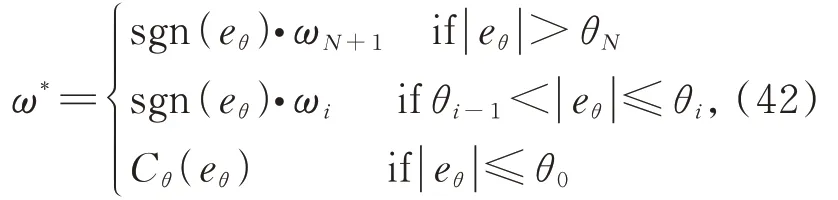
其中：i=1，2，...，N，ω*是位置控制環(huán)的輸出，eθ=θref-θ是位置誤差，θref是位置參考值，θ是位置反饋值，θ0＜θ1＜…＜θN是預(yù)設(shè)的閾值，ω1＜ω2＜…＜ωN+1是位置控制環(huán)輸出的常值，Cθ是位置閉環(huán)控制器。該方法的缺點(diǎn)在于分段的過程比較依賴經(jīng)驗(yàn)值，例如θi，ωi以及分段數(shù)N的選擇都需要通過多次試驗(yàn)，才能使所設(shè)計(jì)的分段參數(shù)與物理系統(tǒng)的實(shí)際響應(yīng)相匹配，否則如果切入閉環(huán)的速度過大或者過小，都會(huì)影響系統(tǒng)的響應(yīng)品質(zhì)。另外，一旦物理系統(tǒng)的最大速度或者最大加速度發(fā)生改變（例如系統(tǒng)的轉(zhuǎn)動(dòng)慣量發(fā)生改變、或者驅(qū)動(dòng)器的驅(qū)動(dòng)電流、驅(qū)動(dòng)電壓發(fā)生改變等），均需要對分段進(jìn)行重新設(shè)計(jì)，否則會(huì)出現(xiàn)因分段與系統(tǒng)響應(yīng)能力不匹配所造成的響應(yīng)過慢或者超調(diào)等現(xiàn)象。

4.3 VLTD 在地平式大視場望遠(yuǎn)鏡快速定位中的應(yīng)用

將帶有速度和加速度飽和限制的VLTD 應(yīng)用于望遠(yuǎn)鏡軸系的快速調(diào)轉(zhuǎn)定位中，并且與傳統(tǒng)的位置分段控制方式進(jìn)行對比實(shí)驗(yàn)。實(shí)驗(yàn)對象是某1 m 級地平式大視場望遠(yuǎn)鏡的方位軸，軸系采用交流永磁同步電機(jī)驅(qū)動(dòng)，驅(qū)動(dòng)器和控制器硬件平臺采用DSP+FPGA，驅(qū)動(dòng)電源采用48 V 的開關(guān)電源，驅(qū)動(dòng)電流的最大值為10 A，位置反饋信號采用29 位絕對式編碼器測量，速度反饋信號通過位置反饋信號差分并濾波后得到，控制方式采用電流+速度+位置的三閉環(huán)方式，控制框圖如圖8 和圖9 所示。其中，圖8 的位置環(huán)采用傳統(tǒng)的位置分段控制方式，圖9 的位置環(huán)采用VLTD進(jìn)行位置參考信號的過渡。除了位置誤差的處理方式不同，兩者的三環(huán)控制器設(shè)計(jì)完全相同，電流控制器的設(shè)計(jì)采用傳統(tǒng)的PI 控制器，速度環(huán)控制器采用ADRC 控制方式，具體設(shè)計(jì)方法見文獻(xiàn)［19］，此處不再贅述，位置環(huán)控制器采用最簡單的比例控制器。

圖8 采用位置分段的控制框圖Fig. 8 Control diagram of position section method

圖9 采用VLTD 的控制框圖Fig. 9 Control diagram of VLTD method

在進(jìn)行位置環(huán)分段以及VLTD 的設(shè)計(jì)之前，均需要對系統(tǒng)的最大反饋能力進(jìn)行摸底測試，得到系統(tǒng)的最大反饋速度為20.5（°）/s，最大加速度約為19.6（°）/s2。在不存在機(jī)械限位的前提下，根據(jù)就近調(diào)轉(zhuǎn)原則，方位軸的最大調(diào)轉(zhuǎn)步長為180°。為了驗(yàn)證系統(tǒng)對不同步長的位置響應(yīng)能力，用兩種實(shí)驗(yàn)方法分別進(jìn)行2°～180°之間不同階躍步長的位置階躍實(shí)驗(yàn)，其中位置環(huán)分段參數(shù) 取 值 為：N=8，θ0=0.01°，θ1=0.017°，θ3=0.28°，θ4=1.1°，θ5=2.2°，θ6=11°，θ7=22°，θ8=33°；ω1=0.1(°)/s，ω2=0.2(°)/s，ω3=0.5(°)/s，ω4=1.9(°)/s，ω5=3.8(°)/s，ω6=5.3(°)/s，ω7=11.8(°)/s，ω8=16.7(°)/s，ω9=20(°)/s。

圖10～圖13 分別給出了幾個(gè)典型的實(shí)驗(yàn)結(jié)果，其中p0=2°，10°，30°和180°。可以看出，使用位置分段的方式均能夠達(dá)到無超調(diào)的響應(yīng)效果，但是由于分段的設(shè)置，在減速的過程中不能夠充分發(fā)揮系統(tǒng)的最大減速能力，所以減速段的時(shí)間明顯變長。

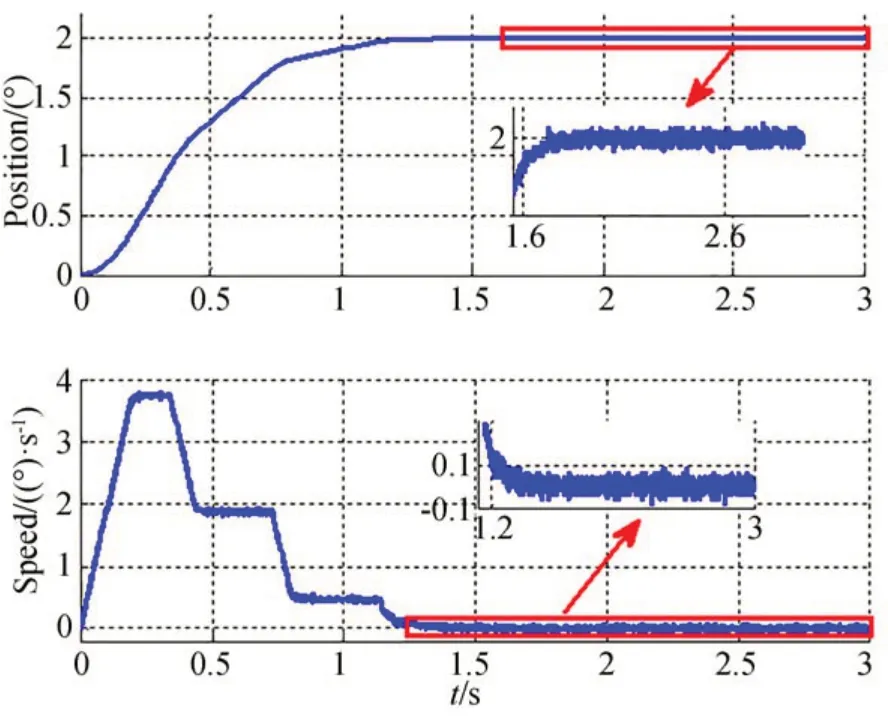
圖10 當(dāng)p0=2 時(shí)的位置階躍響應(yīng)Fig.10 Position step response with p0=2

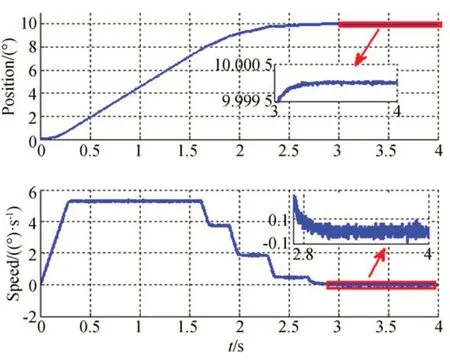
圖11 當(dāng)p0=10 時(shí)的位置階躍響應(yīng)Fig.11 Position step response with p0=10

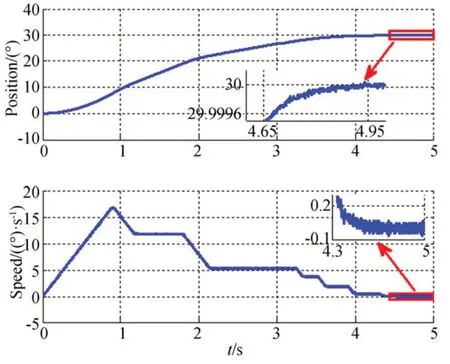
圖12 當(dāng)p0=30 時(shí)的位置階躍響應(yīng)Fig.12 Position step response with p0=30

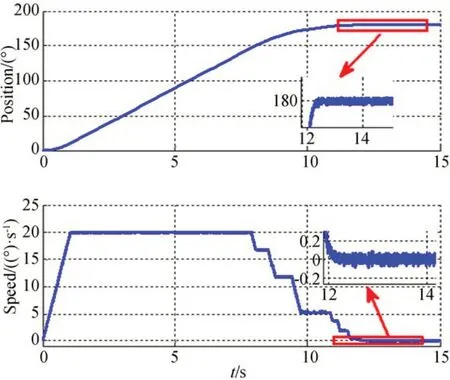
圖13 當(dāng)p0=180 時(shí)的位置階躍響應(yīng)Fig.13 Position step response with p0=180

使用VLTD 過渡的實(shí)驗(yàn)中，參數(shù)取值為h=0.001，σ=2.3，r=19，Vmax_VLTD=20。為了驗(yàn)證VLTD 的輸出速度作為速度前饋的作用，分別完成了帶有速度前饋和不帶有速度前饋的實(shí)驗(yàn)，幾組典型的實(shí)驗(yàn)結(jié)果如圖14～圖17 所示。從實(shí)驗(yàn)結(jié)果可以看出，使用帶速度和加速度限制的VLTD 安排的過渡過程能夠按照預(yù)設(shè)的速度和加速度引導(dǎo)望遠(yuǎn)鏡軸系運(yùn)動(dòng)，在加速和減速段都能夠充分發(fā)揮出系統(tǒng)的反饋能力。

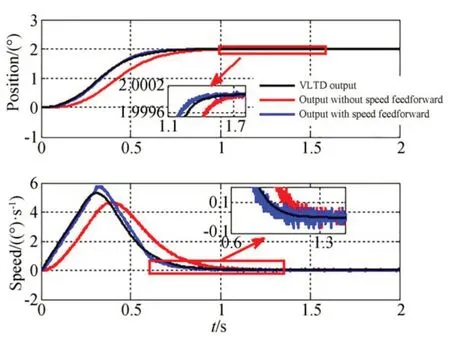
圖14 當(dāng)p0=2 時(shí)的位置階躍響應(yīng)Fig.14 Position step response with p0=2

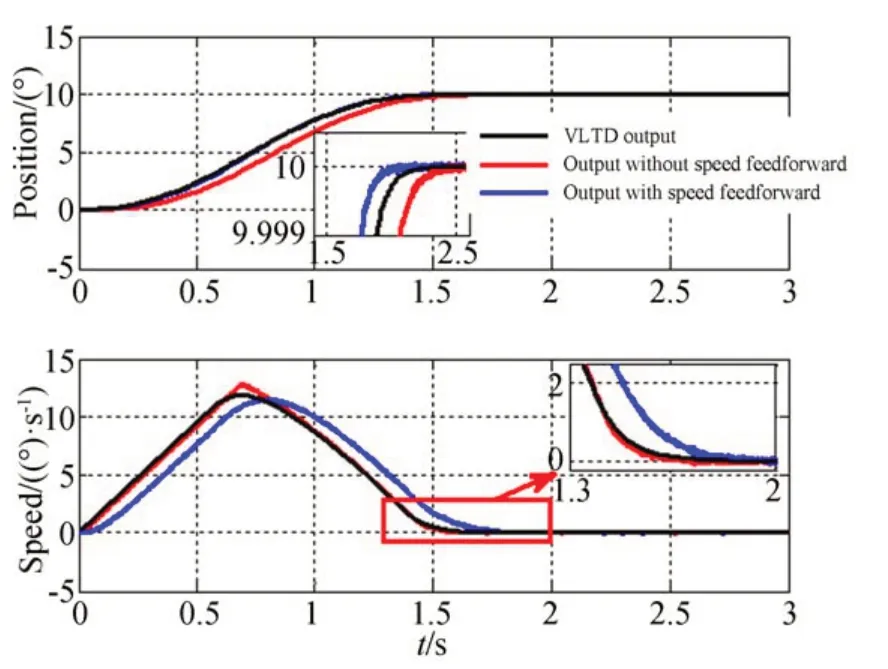
圖15 當(dāng)p0=10 時(shí)的位置階躍響應(yīng)Fig.15 Position step response with p0=10

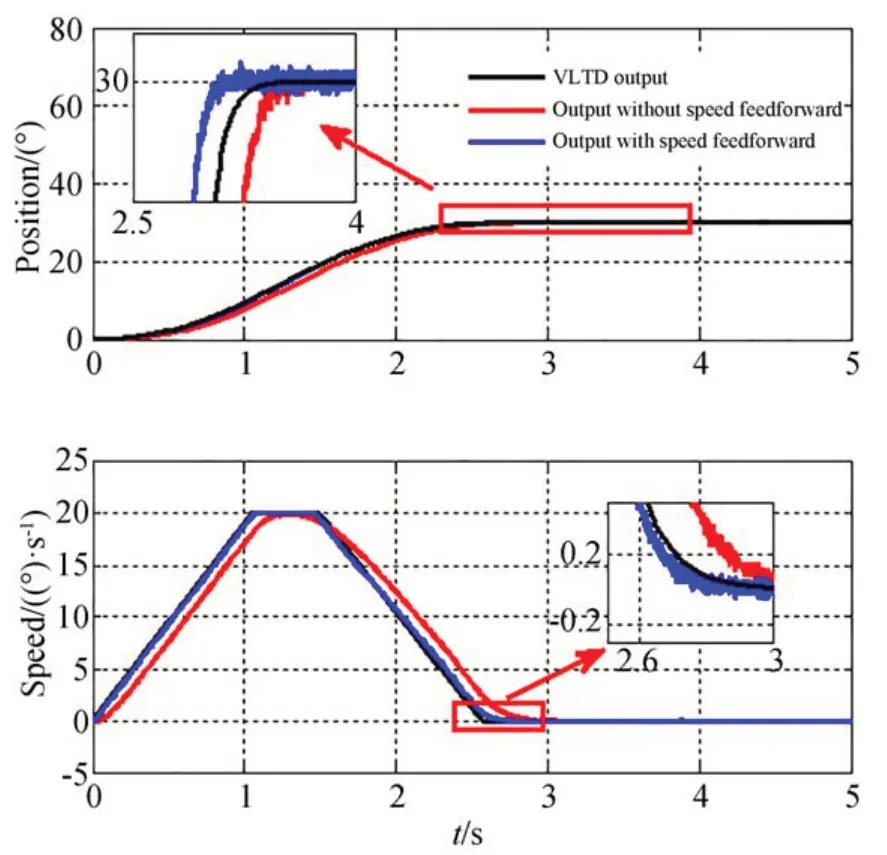
圖16 當(dāng)p0=30 時(shí)的位置階躍響應(yīng)Fig.16 Position step response with p0=30

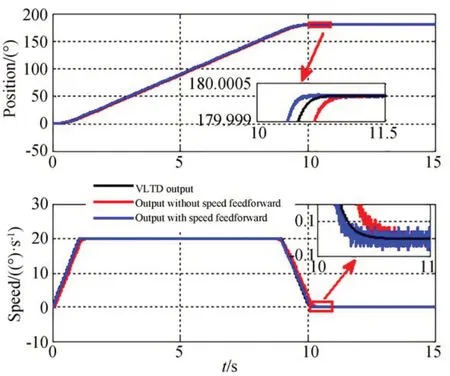
圖17 當(dāng)p0=180 時(shí)的位置階躍響應(yīng)Fig.17 Position step response with p0=180

表2 列出了實(shí)驗(yàn)中位置響應(yīng)進(jìn)入5″誤差帶的時(shí)間t1和1″誤差帶的時(shí)間t2，它定量地描述了不同實(shí)驗(yàn)方法的效果。可以看出，使用VLTD 安排過渡過程的方式可以使得動(dòng)態(tài)響應(yīng)時(shí)間明顯變短，并且利用VLTD 的第二個(gè)輸出作為速度前饋能夠進(jìn)一步縮短響應(yīng)時(shí)間，與位置分段方法相比，響應(yīng)時(shí)間縮短了大約15%～37%，有效地提高了望遠(yuǎn)鏡的搜索效率，對于大視場望遠(yuǎn)鏡具有重要的意義。

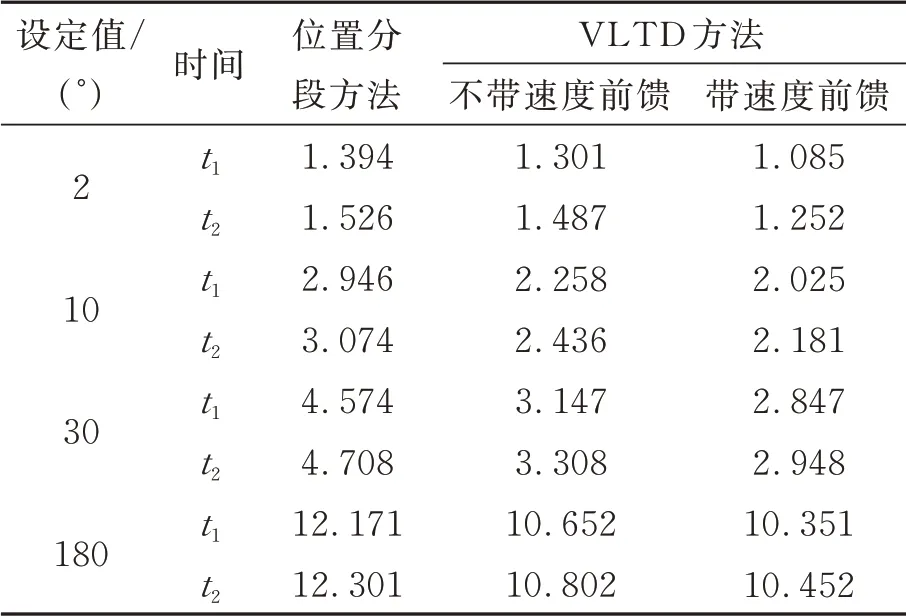
表2 位置響應(yīng)進(jìn)入5″和1″誤差帶的時(shí)間Tab.2 Time points for position response in 5″and 1″position error bands （s）

對比實(shí)驗(yàn)中只給出了一種分段取法，雖然通過增加分段數(shù)N以及優(yōu)化分段策略可以進(jìn)一步提高該方法的響應(yīng)速度，但是優(yōu)化過程需要進(jìn)行大量的實(shí)驗(yàn)，而且分段數(shù)N越多，程序的計(jì)算復(fù)雜度越高，也不利于程序的二次移植。而本文給出的VLTD 設(shè)計(jì)方法，參數(shù)設(shè)定方法簡單，只需測量物理系統(tǒng)的最大反饋速度和加速度，就可以進(jìn)行參數(shù)的設(shè)定，且程序可以進(jìn)行快速移植。

5 結(jié) 論

本文給出了一種為物理信號安排過渡過程的工具——變參數(shù)線性跟蹤微分器，它是在分析已有線性跟蹤微分器安排過渡過程的不足基礎(chǔ)上提出的，所給出的過渡過程能夠很好地與物理系統(tǒng)的反饋能力相匹配，在起到過渡作用的同時(shí)，又能夠充分發(fā)揮系統(tǒng)的最大反饋能力。從理論上對VLTD 的收斂性進(jìn)行了證明，并且給出了仿真計(jì)算。將VLTD 應(yīng)用于地平式大視場望遠(yuǎn)鏡的快速調(diào)轉(zhuǎn)控制中，替代傳統(tǒng)的位置環(huán)基于位置誤差的分段控制方式，實(shí)驗(yàn)結(jié)果表明，在各種不同大小步長的位置階躍響應(yīng)中，響應(yīng)時(shí)間可以縮短大約15%～37%，大大提高了望遠(yuǎn)鏡的搜索效率。所設(shè)計(jì)的安排過渡過程方法的參數(shù)簡單易設(shè)置，利于在工程中的調(diào)試和實(shí)現(xiàn)。

本文中的分析以及實(shí)驗(yàn)均是針對常值信號進(jìn)行的，VLTD 也可應(yīng)用于對時(shí)變信號的過渡過程安排，在后續(xù)工作中會(huì)對VLTD 跟蹤時(shí)變信號的性質(zhì)進(jìn)行分析。