地基大口徑望遠鏡重力彎曲引起的指向變化檢測與修正

王洪浩，王建立，陳 濤，曹玉巖，陳寶剛

（1. 中國科學院 長春光學精密機械與物理研究所，吉林 長春 130033；2. 中國科學院大學，北京 100049）

1 引 言

隨著口徑的不斷增大，望遠鏡的尺寸相應增加且結構越來越復雜，重力場變化引起的望遠鏡光軸指向變化影響也愈發明顯，進而影響望遠鏡的跟蹤精度，望遠鏡的指向變化檢測與修正已成為研究的熱點和難點［1］。

以中國科學院長春光機所4 m 望遠鏡為例，在跟蹤過程中采用獨立結構的捕獲跟蹤器進行閉環跟蹤，裝調過程中確認跟蹤器的光軸與主次鏡光學系統光軸的平行度是至關重要的。但是由于跟蹤過程中望遠鏡俯仰角的變化和受到站址的限制，兩者光軸并沒有嚴格保持平行，引入跟蹤誤差，重力彎曲會導致圖像運動，這是大型地基望遠鏡的普遍問題。在望遠鏡跟蹤與指向誤差修正方面，歐洲南方天文臺ESO 在NTT 望遠鏡上提出了一種基于主動光學的校正技術［2］，使用圖像傳感元件來觀察望遠鏡跟蹤與指向信息的變化，以此作為反饋來調節副鏡的位置以校正跟蹤與指向信息誤差。該系統隨后被應用于8～10 m 量級的巨型地基望遠鏡［3-7］。其中，VLT望遠鏡使用3 個單獨的調節機制來逐一調節跟蹤與指向信息的誤差，TNG［4］和VST［8］使用副鏡調節平臺來彌補光軸的變化。Gemini 近紅外光譜儀（GNIRS）使用單個敏感光學器件的可調節懸臂式鉸鏈，在設計過程中對比重力影響，并通過驅動連接到準直器上的傾斜偏擺鏡進行調整［9］。對于正在建設的NOAO 極寬視場紅外馬賽克相機（NEWFIRM），整個光學系統的支撐結構相對于望遠鏡焦平面的偏轉和精確旋轉可以進行機械調整，光學系統保持在焦平面的一個固定位置上，使科學探測器上的圖像運動最小化［9］。

國內天文望遠鏡一般利用統計的方法建立望遠鏡的指向誤差模型，從而修正望遠鏡機械制造安裝和光軸變化引起的指向誤差［10-11］。常用的望遠鏡指向誤差修正軟件有STRAC 和TPOINT 等［12-14］，它們基于物理參數及經驗修正望遠鏡指向，但僅利用指向模型進行大型地基望遠鏡誤差修正具有局限性。云南天文臺針對1 m 紅外太陽望遠鏡，提出了檢測光電導行系統光軸與主光學系統光軸之間相對變化的方法［15］。

從原理上，指向誤差可以通過改變主光學系統光軸來補償，而主鏡相對于跟蹤架來說位置是固定的，因此，需要改變次鏡相對于主鏡的空間位置，那么次鏡需要在空間5 個自由度上可調。以4 m 望遠鏡為例，其次鏡調整平臺為Hexapod平臺，具有剛度大、調整自由度多、位置誤差不累計等優點［4-5，7-9］。在實際應用中，采用Hexapod 平臺調整次鏡來校正主次鏡光軸變化通常有兩種工作模式：一種是閉環模式，如VST［8］，以圖像傳感器反饋的指向誤差作為反饋，實時調整次鏡的位置；另一種是開環模式，通過望遠鏡在不同俯仰角度狀態下觀測恒星，標定出次鏡位置，工作時采用查表方式來實現指向誤差補償。4 m 望遠鏡的跟蹤精度要求是0.1（″）/min。盡管設計考慮到了光軸的變化和主次鏡光學系統的機械安裝彎沉，但當望遠鏡投入運行時，捕獲跟蹤器的光軸和主次鏡光學系統光軸的相對位置變化并不可知。本文根據4 m 望遠鏡的結構，分析了閉環跟蹤時主光學系統光軸變化引入的跟蹤誤差的變化規律，提出了望遠鏡光軸變化的檢測方法，并提出基于次鏡支撐結構（Hexapod 平臺）及卡式系統零彗差點理論的修正模型，來提高地基大口徑望遠鏡的跟蹤性能與指向誤差修正能力。

2 望遠鏡系統結構

4 m 級地基望遠鏡系統如圖1（a）所示，總體高度為12.5 m，寬度為5.8 m，質量接近90 t。望遠鏡主要包括地平式跟蹤架、主鏡、次鏡、機上標定系統、庫德系統、機下自適應成像系統及多個成像終端等，這里為了簡化分析流程，僅考慮前六部分。望遠鏡焦面位于機下庫德房平臺平面，該平臺放置4 m 望遠鏡的多個終端系統，包括精跟蹤系統、波前探測系統及高分辨率成像系統。如圖1（b）所示，主鏡M1 是拋物面反射鏡，次鏡M2 為雙曲面凸反射鏡，M3 是橢球平面反射鏡，M4～M6 組成庫德系統且均為平面反射鏡，F1 是主系統焦點，具體的光學參數如表1所示。

圖1 4 米望遠鏡示意圖Fig.1 Schematic diagram of 4 m telescope

表1 4 米望遠鏡的具體參數Tab.1 Specifications of 4 m telescope

望遠鏡主鏡安裝與四通結構內部，四通結構外部裝有口徑為400 mm 的捕獲跟蹤器，如圖1（c）所示，望遠鏡系統通過捕捉目標的圖像，允許主次鏡光學系統在長時間內高精度地追蹤區域目標。這種帶有獨立捕獲跟蹤系統的閉環追逐模式，需要望遠鏡主次鏡光學系統的光軸和捕捉跟蹤器的光軸在整個跟蹤過程中應在同一天區內指向一致，即兩個光學系統光軸保持嚴格平行。望遠鏡通過地平式跟蹤架進行觀測，為了消除望遠鏡的準直誤差及零點誤差，采用對同一恒星的兩種狀態進行多次觀測，兩種狀態的方位指向相差180°、俯仰指向相差2 倍天頂距，由此可以消除準直誤差及零點誤差的影響［16］。

圖像在望遠鏡視場內的旋轉是大型水平式地基望遠鏡在目標跟蹤時最重要的特征之一。這種旋轉除了受望遠鏡自身光學系統的影響外，還受地平目標系內目標變化規律的影響。

根據圖1（b）和圖1（c），4 m 望遠鏡具有庫德折轉系統，主光學系統與捕獲跟蹤系統中的像旋轉是完全不同的。為了消除像旋對地基望遠鏡的影響，在4 m 望遠鏡的成像終端采用道威棱鏡消旋系統，消除目標在地平坐標系及庫德光路中的像旋。

3 望遠鏡光軸變化引入的跟蹤誤差分析

3.1 引起光軸指向變化的因素分析

造成捕獲跟蹤器與主次鏡光學系統光軸改變的原因有許多。首先，支撐主、次鏡的桁架結構系統受重力變形引起主鏡及次鏡之間相對位置變化，從而導致光軸改變［17-19］，4 m 望遠鏡主鏡采用主動光學技術實現位置閉環，次鏡支撐結構及桁架質量達到2 t，重力引起的形變量是引起光軸變化的主要原因。然后，捕獲跟蹤器成像終端探測器支撐結構在不同俯仰角條件下受重力影響也會導致光軸變化，4 m 望遠鏡主系統的成像探測器位于機下平臺內，不受重力場變化的影響。最后，400 mm 口徑捕獲跟蹤的質量達到500 kg，捕獲跟蹤器與望遠鏡四通接口的安裝基座在不同俯仰角下受重力的影響會導致光軸變化［20］。因此，望遠鏡觀測時所有影響因素疊加造成的光軸變化及其規律相當復雜。光軸變化最終會導致捕獲跟蹤器對目標成像點閉環跟蹤后的殘余跟蹤誤差。

現有的光軸變化測量方法有很多［21-24］，均是對光學系統特點進行詳細分析后得出測量結果。而4 m 望遠鏡系統的高度達到了12.5 m，采用附加機構對系統光軸變化進行檢測是復雜且很難實現的，附加機構不僅存在損壞設備的風險，而且會影響望遠鏡的正常觀測。國外有些學者采用高精度的偏離誤差仿真模型來處理大型地基天文望遠鏡在機械安裝與調試過程中引入的跟蹤與指向誤差，如望遠鏡主次鏡之間的光軸變化引入的相對位置變化偏差。常用的望遠鏡指向誤差修正軟件有STARCA 和TPOINT，它們采用的是經驗修正及參數修正，精度相對較低。光軸變化引起的誤差與望遠鏡方位軸和俯仰軸不是垂直正交的實際情況有很大關聯，并且指向精確度模型只針對望遠鏡主次鏡光學系統的光軸變化進行補償。4 m 望遠鏡還要考慮捕獲跟蹤系統偏差和其他因素導致的光軸變化，即主光學系統的光軸與捕獲跟蹤器光軸之間的相對變化。

3.2 重力變形引入光軸偏差分析

本文采用有限元法建立望遠鏡不同俯仰角條件下的結構模型，如圖2 所示。該狀態下視為準靜態模型［25］，結構力學方程可以表達為：

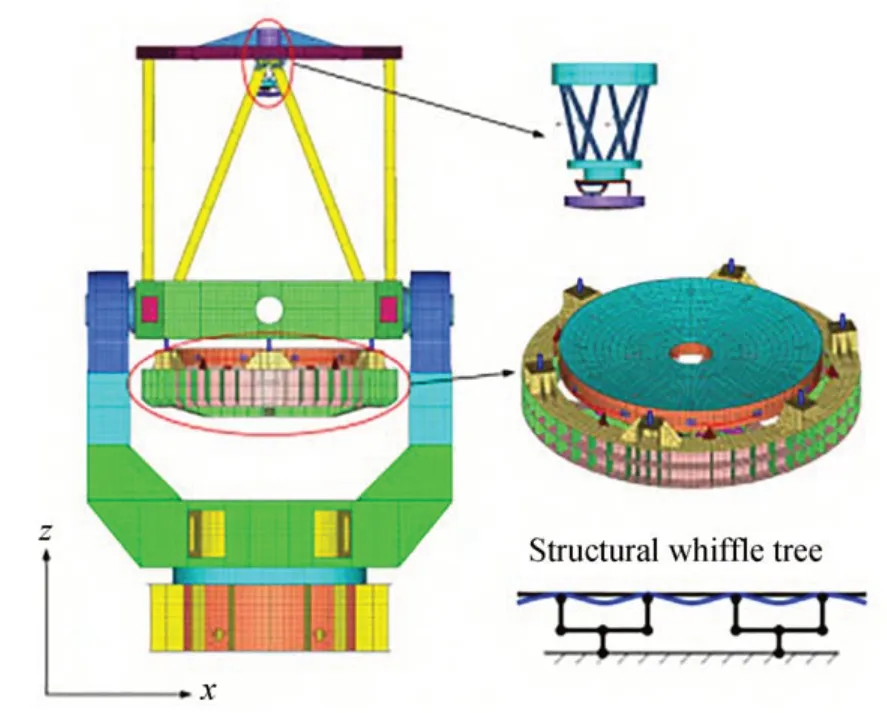
圖2 望遠鏡結構的有限元模型Fig. 2 Finite element model of four-meter telescope

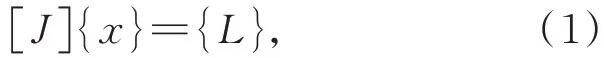
式中：[J]為望遠鏡剛度矩陣，{x}為位移向量，{L}為載荷向量。

在望遠鏡觀測過程中，引起光軸變化的主要原因是主次鏡相對位置的改變，因此在對望遠鏡進行結構建模仿真時更關注次鏡相對于主鏡鏡面節點的位置變化。以主鏡為基準，次鏡相對于主鏡選取節點位移可表達為：

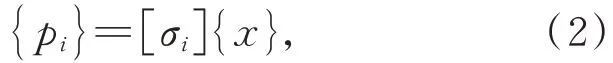
式中：{pi}為次鏡鏡面節點位移向量，[σi]為次鏡相關的旋轉矩陣。

由式（1）和式（2）可知，次鏡相對于主鏡的位置表達為：

式（3）給出了相對于主鏡次鏡鏡面上各個節點的位置信息，根據次鏡的二次曲面公式進行最小二乘法擬合可得到次鏡相對于主鏡的空間位置，得出主次鏡在不同俯仰角度情況下的角度偏差仿真結果，如圖3 所示，位置偏差仿真結果如圖4 所示。

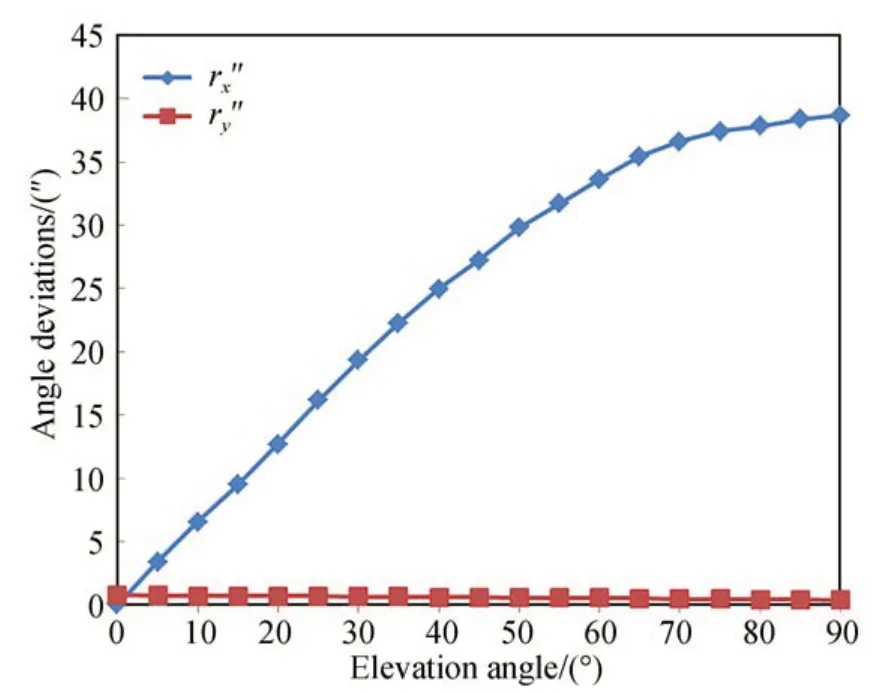
圖3 主次鏡角度偏差隨俯望遠鏡仰角度的變化Fig.3 Angle deviations between primary and secondary mirror vs. elevation angle of telescope

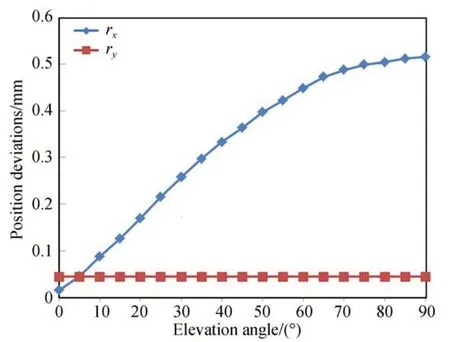
圖4 主次鏡位置偏差隨望遠鏡俯仰角度的變化Fig.4 Position deviations between primary and secondary mirror vs. elevation angle of telescope

將仿真分析結果中的位置偏差及角度偏差作為輸入，分析望遠鏡光學模型中主系統的光軸偏差，光軸偏差隨俯仰角的變化如圖5 所示。

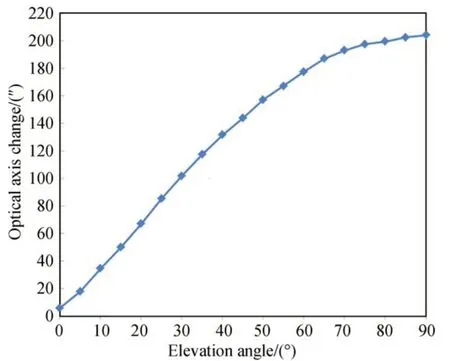
圖5 主系統光軸偏差隨望遠鏡俯仰角的變化Fig.5 Optical axis change of primary optical system vs.elevation angle of telescope

3.3 光軸指向變化測量原理

根據上述分析，引起光軸指向變化的主要因素為次鏡相對于主鏡的傾斜及平移、跟蹤探測器與主系統光軸傾斜，如圖6 所示。次鏡相對于主鏡產生的位移為h1，次鏡相對于主鏡產生的傾斜為θ1，捕獲跟蹤器相對于主系統光軸傾斜為θ2，它們對目標在成像CCD 上的影響為［25］：

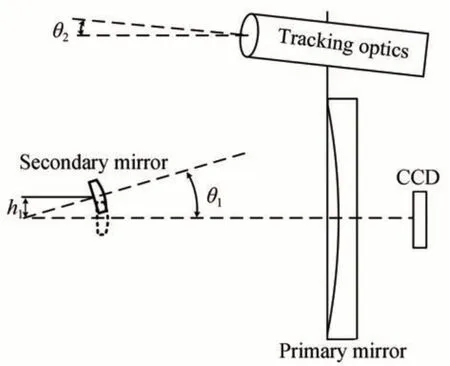
圖6 主系統與跟蹤器傾斜和平移示意圖Fig.6 Relative rotation and displacement between primary optical system and tracking optics

其中：S為次鏡到成像CCD 的距離，R為次鏡曲率半徑，F1為捕獲跟蹤器的焦距。

為了簡化，將捕獲跟蹤器光軸與主系統光軸傾斜偏差統一考慮為重力場變化帶來的指向誤差，在觀測過程中這部分指向誤差可以通過移動次鏡來補償。考慮到4 m 望遠鏡高度達到12.5 m，在次鏡位置放置標定光源是簡單且可行的方案。標定光源位于次鏡中心位置，在主光學系統裝調過程中，通過基準轉移的方式使標定光源與主光學系統光軸重合。光源發出的光隨著次鏡及桁架移動，經過三鏡及庫德系統將光束折轉至機下成像探測器。光軸指向變化測量光路如圖7所示。

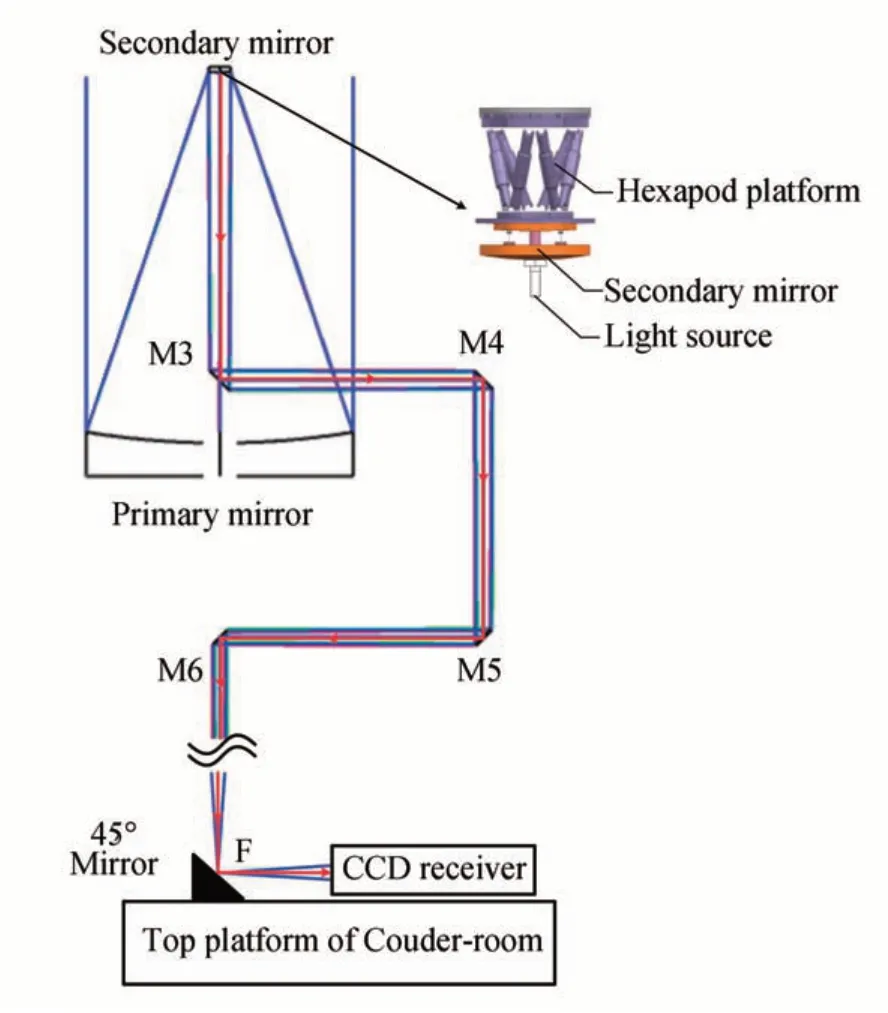
圖7 測定光軸指向變化示意圖Fig.7 Schematic diagram of determining telescope optical axis change

模擬光源與目標成像所經過的路徑唯一的區別為目標成像經過主次鏡進行成像，而模擬光源沒有經過主次鏡。在模擬光源光軸與主光學系統光軸重合的前提下，標定光源和目標成像的影響基本相同，均可通過標定光源的相對測量進行修正。圖像采集步驟為：標定光源隨俯仰角變化（間隔5°俯仰角）采集10 幅圖像，針對恒星隨俯仰角變化（間隔5°俯仰角）采集50 幅圖像。在此過程中，望遠鏡系統狀態是固定不變的，俯仰角變化前后采集圖像平均坐標值的差值即為望遠鏡主系統的光軸指向變化。

4 實驗與結果

對4 m 望遠鏡光軸指向變化進行實測與分析，圖8 和圖9 分別為標定光源與恒星圖像脫靶量隨望遠鏡俯仰角的變化值。由圖可知，兩者基本呈二次曲線變化，與分析結果相符合。在對恒星標校過程中，低于20°俯仰角時4 m 口徑望遠鏡色散現象明顯［21］，成像系統脫靶量提取精度下降，因此在恒星俯仰角為20～85°時對望遠鏡進行標定。

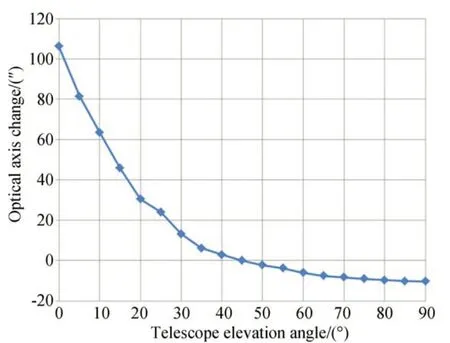
圖8 標定光源測定光軸指向隨望遠鏡俯仰角的變化Fig.8 Optical axis change of primary optical system by light source vs. angle of telescope elevation

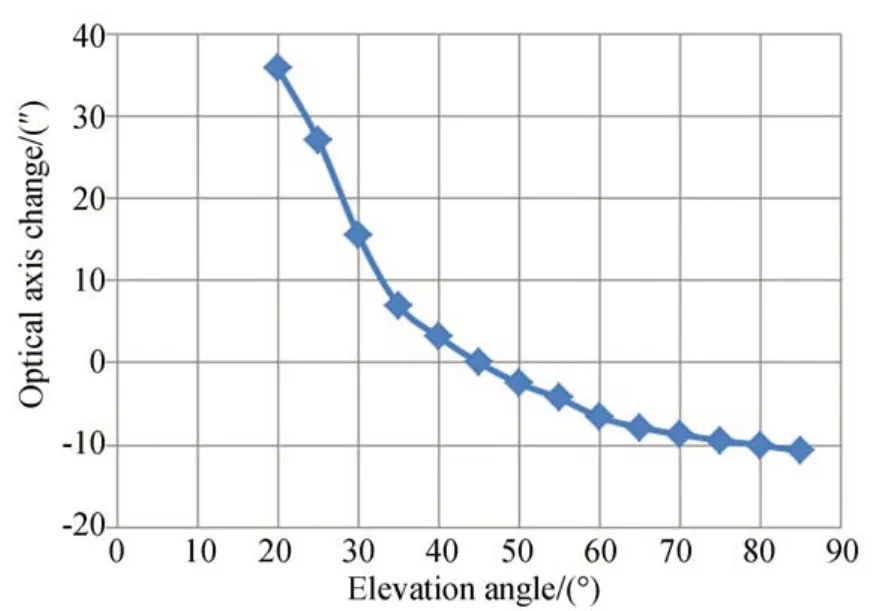
圖9 恒星像測定光軸指向隨望遠鏡俯仰角的變化Fig.9 Optical axis change of primary optical system by star vs. elevation angle of telescope

望遠鏡裝配過程中，在俯仰角為45°時對捕獲跟蹤器與主光學系統進行標校，并以此時的光軸為基準零點。俯仰角較高時望遠鏡指向變化不明顯，而在低仰角工作時望遠鏡的指向變化幅值較大，這是因為望遠鏡桁架結構受重力的影響，低仰角時整體力矩變大從而對望遠鏡指向影響較大。

實驗結果表明，望遠鏡低仰角時，光軸最大相對變化為126″，望遠鏡桁架結構在重力場的變化是引起俯仰角相關指向變化的主要因素。由于4 m 望遠鏡整體尺寸較大，光學系統光路總長達到50 m 以上，偏離擬合趨勢的采樣點對應望遠鏡主系統及庫德光路中大氣異常折射及望遠鏡低頻擾動的影響，真實地反映了望遠鏡光學指向不隨俯仰角變化的系統誤差。對比標定光源與恒星像取得的數據，在相同俯仰角下恒星像的光軸指向變化比標定光源要小。考慮到采集數據時標定光源安裝在次鏡桁架結構上，隨著望遠鏡桁架結構在重力作用下運動，因此采樣數據存在一定的偏差，在數據處理過程中要以實際測量的恒星像為主。

5 望遠鏡光軸補償與分析

5.1 基于卡式系統零彗差點理論的修正模型

卡式結構的望遠鏡系統在光軸上發生位移，像差體現為離焦和球差，它們可以通過在軸向移動副鏡來校正。垂直光軸發生位移和傾斜，像差是視場內的恒定彗差，可以通過在垂直光軸上移動或傾斜副鏡來校正。如果不考慮鏡面面形的修正，望遠鏡系統誤差為主、次鏡的相對位置誤差。對于在軸上的視場，如果校正了像差，主、次鏡的中心軸相交于零彗星點［22］，如圖10 所示。

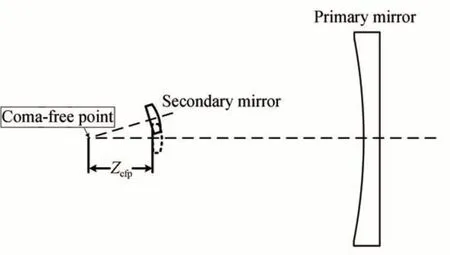
圖10 零彗差點示意圖Fig.10 Schematic diagram of coma-free point

零彗差點與理想情況下次鏡中心頂點距離Zcfp滿足：

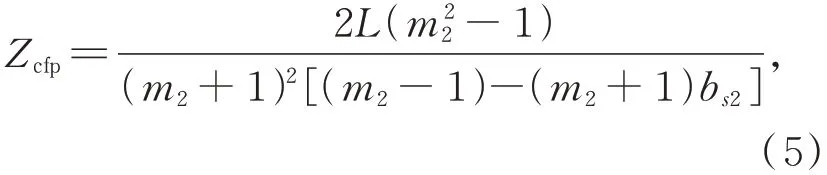
式中：L為理想情況下次鏡中心頂點與焦面中心的距離，m2為次鏡放大率，即系統焦距與主鏡焦距之比，滿足m2=f'/f1'，f'為望遠鏡系統的焦距，f1'為主鏡的焦距，bs2為次鏡的非球面系數。若繞該點旋轉，次鏡的平移D和旋轉T產生的彗差在軸上視場始終可以相互抵消，但此時次鏡相對于主鏡的相對位置發生變化，改變了望遠鏡主光學系統的光軸。因此，在軸上視場得到校正前提下，通過次鏡繞零彗差點旋轉可以改變主光學系統的指向。以望遠鏡機下平臺成像探測器脫靶量為反饋，作為確定光軸的校正依據，最終實現望遠鏡指向的修正。

5.2 望遠鏡光軸補償結果與討論

根據次鏡當前位置，利用無彗差點理論計算主次鏡的無彗差旋轉點位置。以無彗差旋轉點為基準，以機下成像相機脫靶量為反饋，計算Hexapod 平臺各個維度的輸入量，對地基大口徑望遠鏡主次鏡引起的光軸偏差進行補償。補償后，望遠鏡次鏡相對于主鏡光軸角度偏差隨俯仰角度的變化如圖11 所示，位置偏差隨俯仰角度變化如圖12 所示，望遠鏡主系統光軸偏差隨俯仰角的變化如圖13 所示。

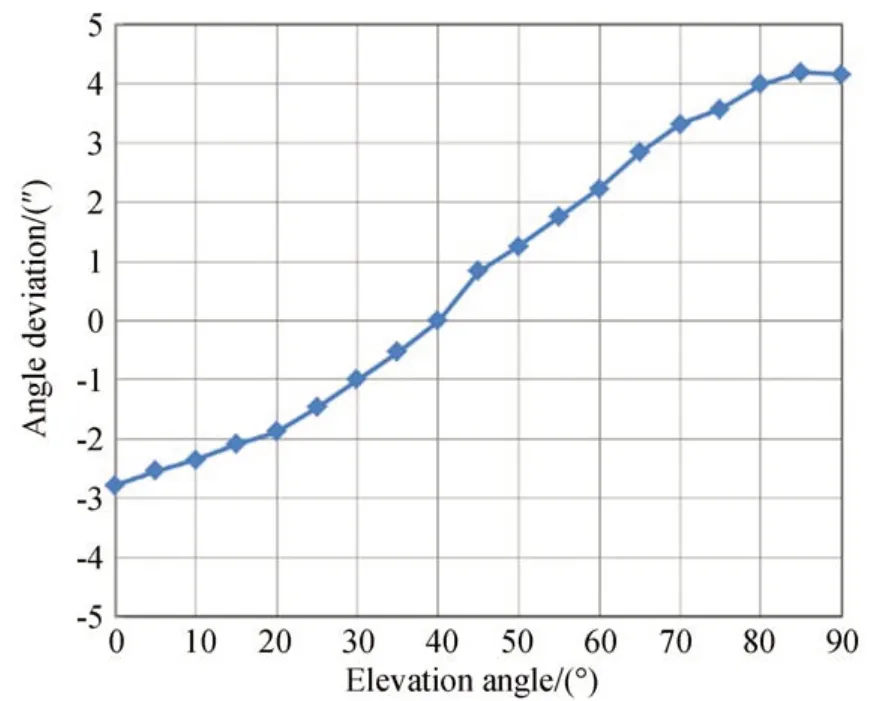
圖11 補償后次鏡相對于主鏡光軸角度偏差隨俯仰角度的變化Fig.11 Angle deviations between primary and secondary mirror after calibration vs. elevation angle of telescope

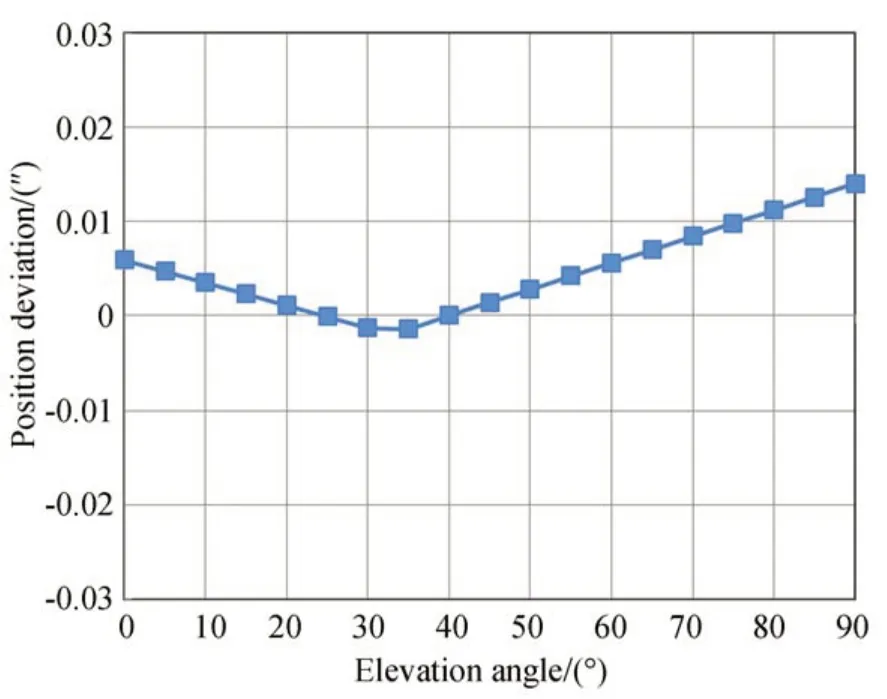
圖12 補償后次鏡相對于主鏡位置偏差隨俯仰角度的變化Fig.12 Position deviations between primary and secondary mirror after calibration vs. elevation angle of telescope

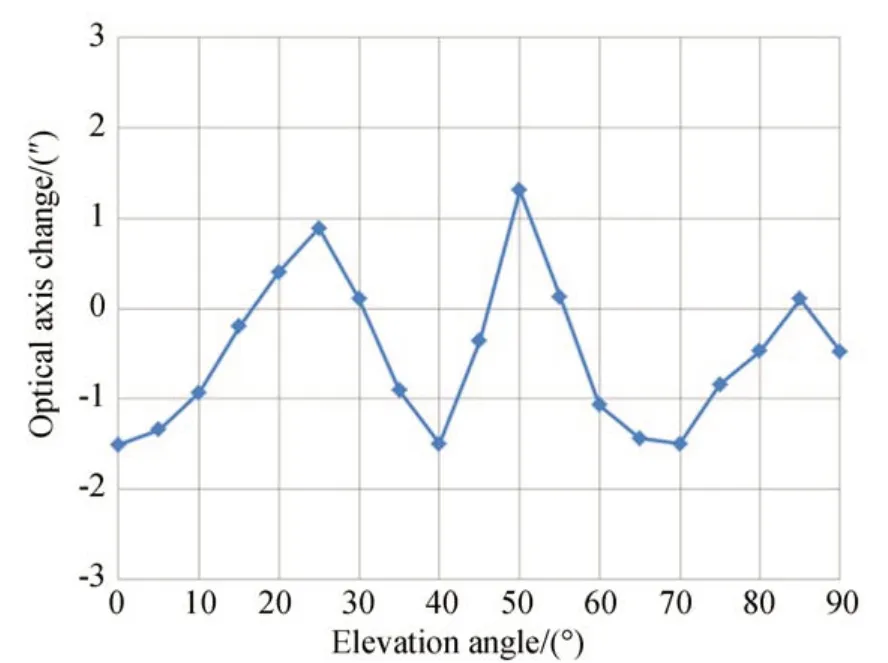
圖13 補償后主系統光軸偏差隨俯仰角的變化Fig. 13 Optical axis change of primary optical system after calibration vs. angle of telescope elevation

補償前，在光軸水平位置次鏡相對于主鏡為最大位置偏差和最大角度偏差，最大角度偏差接近39″，最大位置偏差接近0.5 mm；經過Hexapod 平臺的補償，最大角度偏差下降到7.1″，最大位置偏差下降到0.017 5 mm；與角度偏差相比，補償后位置偏差下降較少，僅由0.5 mm 下降到0.017 5 mm。這是由于在非線性最小二乘擬合過程中忽略次鏡二次曲面擬合誤差的原因，非線性球面擬合來表達次鏡表面節點位置信息，以擬合曲面中心位置與實際次鏡表面二次曲面中心節點的幾何連線作為光軸，此模擬光軸與實際光軸存在一定的擬合偏差，因此主、次鏡的相對位置在初始時便存在一定的偏差。

基于卡式系統主次鏡零彗差點理論將次鏡繞無彗差點旋轉進行光軸補償，不會改變主系統像質，只改變主系統光軸，其實質為次鏡光軸與主鏡光軸的對準。補償前光軸最大偏差為123″，補償后光軸最大偏差下降至2.8″。

6 結 論

本文針對地基大型光學望遠鏡中重力變形導致的光軸偏移，研究了捕獲跟蹤系統與主光學系統光軸偏移的估計、光軸偏差的檢測方法及基于次鏡支撐結構（Hexapod 平臺）調整平臺的主動補償過程。基于有限元方法建立了地基望遠鏡的結構模型，研究了系統光軸指向變化的產生原因、標定及補償，提出了基于卡式系統主次鏡零彗差點理論將次鏡繞無彗差點旋轉進行光軸補償的方法。實驗結果表明：重力變形是導致主光學系統光軸偏移的主要原因，光軸偏移量達到了123″，經過次鏡位置補償及無彗差點旋轉補償，光軸偏移問題得到明顯改善，光軸偏移量下降至2.8″。本文提出的地基大口徑望遠鏡指向變化檢測與修正方法可應用于實際望遠鏡的標定和裝調中。