基于粒子群優(yōu)化的宏觀傅里葉疊層成像位置失配校準

何承剛，朱友強，王 斌*

（1. 中國科學院 長春光學精密機械與物理研究所，吉林 長春 130033；2. 中國科學院大學，北京 100049）

1 引 言

在光學領(lǐng)域中，常用空間帶寬積（Space Bandwidth Product，SBP）［1］描述成像系統(tǒng)的信息傳遞能力，更大的SBP 意味著可以獲取成像目標更多的細節(jié)信息。然而，傳統(tǒng)的光學成像系統(tǒng)受衍射和像差影響，其空間帶寬積被限制在百萬量級，難以滿足現(xiàn)代生物醫(yī)學成像［2］和遠距離成像等領(lǐng)域的需求。為了提高成像分辨率，傳統(tǒng)方法是機械地增加成像系統(tǒng)的口徑，不僅會增加光學像差，還會增加整個系統(tǒng)的體積和質(zhì)量。Zheng等提出了傅里葉疊層成像技術(shù)（Fourier Ptychography，F(xiàn)P）［3］，該技術(shù)能夠?qū)崿F(xiàn)大視場高分辨率成像，且成像效果優(yōu)異，因此一經(jīng)問世便備受關(guān)注。

FP 主要應用于顯微和宏觀成像領(lǐng)域，對于不同的應用場景，成像系統(tǒng)的低分辨率圖像采集方式存在明顯的差異。在傅里葉疊層顯微成像（Fourier Ptychography Microscope，F(xiàn)PM）［4］中，可編程控制的LED 陣列替換傳統(tǒng)顯微成像系統(tǒng)中的照明源，通過點亮不同的LED 改變照明波矢使樣品頻譜產(chǎn)生頻移，然后通過相機捕獲一系列低分辨率圖像。在宏觀FP［5-7］中，則是通過移動相機來采集目標的不同頻譜信息，獲取低分辨率圖像。采集好數(shù)據(jù)后，F(xiàn)P 將捕獲的一系列低分辨率圖像傅里葉變換至頻域，然后將這些圖像融合至頻域中對應的子孔徑位置，最終重建出高分辨率的復圖像。FP 作為一種整合相位恢復［8-12］和合成孔徑［13-16］技術(shù)優(yōu)勢的計算成像技術(shù)，突破了透鏡孔徑帶來的物理限制，能實現(xiàn)大視場的高分辨率成像。

在高分辨率圖像重建過程中，位置失配誤差會導致重建圖像質(zhì)量降低。2012 年，Maiden等［17］提出基于模擬退火的pcPIE 算法，該算法逐個校準失配位置進而提高重建圖像質(zhì)量，但算法耗時較長且容易陷入局部最優(yōu)解。2015 年，Yeh等［18］將整個優(yōu)化問題分解為多個子優(yōu)化問題，在運用高斯-牛頓法更新頻譜子孔徑過程中使用模擬退火算法搜尋光瞳函數(shù)的偏移位置，能夠一定程度上降低失配誤差帶來的影響。但由于大角度照明時獲取圖像的信噪比較低，該算法對位于高頻區(qū)域的頻譜子孔徑的位置校準精度較差。2016 年，Sun 等［19］提出基于模擬退火的pcFPM 算法，該方法引入全局收斂模型，算法初期對明場圖像校準并通過非線性回歸獲取空域失配參數(shù)，然后對全部圖像進行類似操作，從而提高重建圖像質(zhì)量，但由于其性能受到模擬退火算法的限制，LED 陣列失配嚴重時算法可能陷入局部最優(yōu)。2017 年，Liu 等［20］提出了基于牛頓法的sc-FP方法，該方法在頻域?qū)︻l譜子孔徑位置校準，能夠兼顧穩(wěn)定性和校準精度，重建圖像質(zhì)量得以提升，但該方法是局部搜索算法，當誤差范圍較大時可能校準失敗。2018 年，Eckert 等［21］提出了角度自校準方法，先準確識別出明場圖像并進行精確搜索，然后通過模擬退火算法搜尋與暗場圖像對應的頻譜子孔徑位置，該方法能適用于大多數(shù)系統(tǒng)且對像差有良好的魯棒性，但易受噪聲干擾。2021 年，Mao 等［22］提出一種基于遺傳退火算法的位置校正方法，解決了單一使用模擬退火算法易使結(jié)果陷入局部最優(yōu)的問題，有效提高了圖像重建質(zhì)量。隨著深度學習技術(shù)的快速發(fā)展，神經(jīng)網(wǎng)絡算法也應用于超分辨率成像領(lǐng)域［23-26］。2021 年，Zhao 等［27］提出了基于深度學習的位置校準算法，該方法通過構(gòu)建神經(jīng)網(wǎng)絡，將物體的實部、虛部以及頻譜子孔徑位置偏差作為卷積層的權(quán)重，然后對網(wǎng)絡進行訓練獲取頻譜子孔徑的準確位置，提高了重建圖像質(zhì)量，但算法耗時較長。上述位置校準算法主要應用于顯微成像領(lǐng)域，且大多數(shù)算法默認LED 陣列間距相同，因此會引入全局收斂模型校準波矢位置。然而，宏觀成像中相機間距存在不確定性，因此，基于全局收斂模型的校準算法無法應用于遠距離成像場景。

2 原 理

2.1 遠場FP 技術(shù)前向成像模型

如圖1 所示，宏觀FP 成像模型由激光器、空間濾波器、聚焦透鏡、樣品和帶鏡頭的圖像傳感器（Charge Coupled Device，CCD）5 部分組成。激光器發(fā)出的光束經(jīng)空間濾波器濾波后，通過聚焦透鏡對物體進行照明。當光束從物體經(jīng)過距離z傳輸至相機孔徑所在平面時，相機孔徑平面的光場可以通過夫朗和費衍射公式進行計算，因此相機孔徑平面的光場可以表示為：

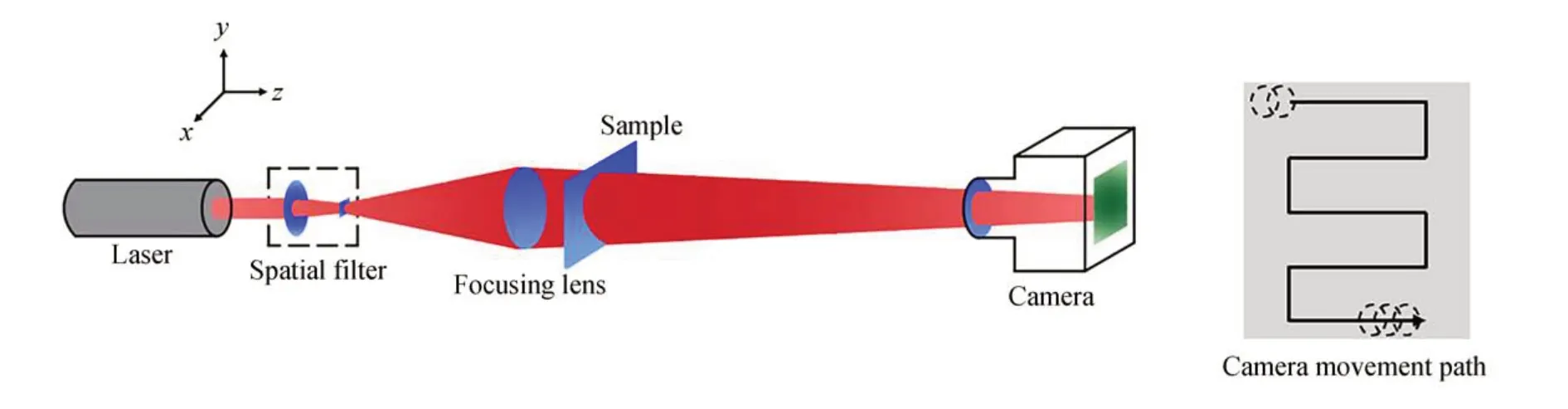
圖1 傅里葉層疊成像模塊示意圖Fig.1 Schematic diagram of Fourier ptychography module

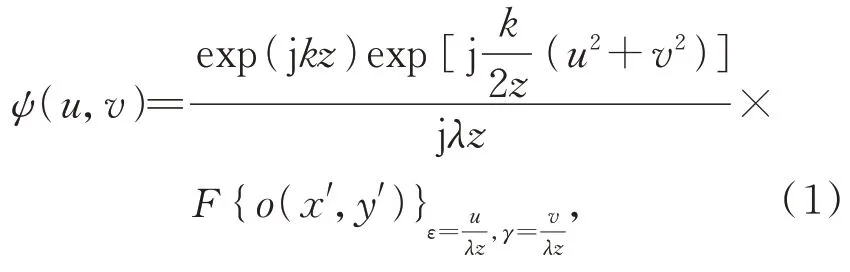
式中：λ表示照明光波長，k=2π/λ表示波數(shù)，o(x'，y')表示物面光場，z表示光束從物面?zhèn)鬏斨料鄼C孔徑平面的距離，ε和λ代表空間頻率，(x'，y')代表物面空間坐標，(u，v)代表相機孔徑平面上的空間坐標。

當光場ψ(u，v)繼續(xù)傳播時，受限于相機鏡頭孔徑大小，只有一部分光場能夠進入相機內(nèi)部并最終成像。相機孔徑等效于一個圓形低通濾波器，能夠進入相機內(nèi)部的光場范圍通常用光瞳函數(shù)P(u，v)來表示，其可以定義為：

式中R為相機孔徑的半徑。部分光場進入相機后從相機鏡頭位置傳播至傳感器所在平面，最終抵達傳感器并成像的光場可表示為：

式中：l是成像距離，f是相機孔徑透鏡焦距，O(u，v)=F{o(x'，y')}，表示物體的頻譜信息。為了方便表示，使用矢量u和x分別表示相機孔徑平面的空間坐標(u，v)和圖像傳感器所在平面的空間坐標(x，y)。由于圖像傳感器只能記錄光強信息，無法捕獲相位信息，所以最終被捕獲的圖像可以表示為：

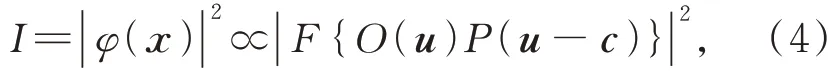
式中c表示相機孔徑的中心位置。

2.2 圖像重建算法

在捕獲一系列低分辨率圖像后，需要通過相位恢復算法重建出高分辨率圖像。首先，需要獲取初始化頻譜O(u，v)以及光瞳函數(shù)P(u，v)。初始頻譜中挑選與第m個位置相機對應的頻譜信息，可以表示為：

煙臺市果樹站于1991年由長富2號中選出的紅富士優(yōu)質(zhì)系列，1997年通過了山東省農(nóng)作物良種評審委員會的審定。果實圓形或長圓形，果形端正，果形指數(shù)0.86～0.89，果個大型，平均單果重245～314克。易著色，樹冠上下、內(nèi)外著色均好，全紅果比例78%～80%，著色指數(shù)95.6%，色澤濃紅艷麗，硬度8.7～9.7公斤/平方厘米，可溶性固形物含量14.8%～15.4%。果實生育期190天，貯藏性跟長富2號相同，綜合性狀優(yōu)于長富2號品種。

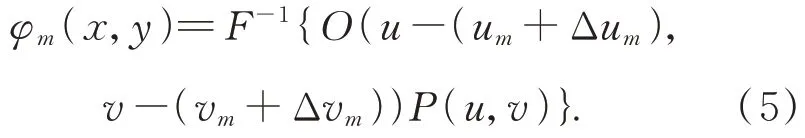
保持從頻譜中截取的復振幅分布φm(x，y)不變，由于相機只能捕獲強度信息，對實際捕獲的低分辨率圖像Im進行處理獲取振幅信息，然后替換φm(x，y)中的振幅信息，可得：

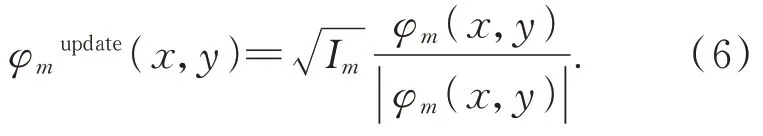
對更新后的復振幅分布進行傅里葉變換獲取頻域信息，然后對樣品頻譜進行更新。重復上述過程，更新樣品頻譜中每一個子頻譜區(qū)域，直至所有相機截取的信息更新完成實現(xiàn)一次迭代，達到預設(shè)迭代次數(shù)后重建出高分辨率圖像。

式（5）中，Δum和Δvm表示頻譜子孔徑的位置偏移，在理想情況下，它們?nèi)≈稻鶠?，即相機的實際位置與理想位置重合，此時不存在相機位置失配問題。理想頻譜子孔徑位置如圖2（c）中藍色圓點所示，此時捕獲的中心低分辨率圖像如圖2（a1）所示，通過相位恢復算法重建出的振幅和相位信息如圖2（a2）和（a3）所示；然而，在宏觀傅里葉疊層成像過程中，需要通過移動相機捕獲低分辨率圖像，移動過程中并不能保證相機處于理想位置，且不同位置的間距并不相同，此時實際頻譜子孔徑位置如圖2（c）中紅色雪花所示（彩圖見期刊電子版）。由于相機位于實際位置時捕獲樣品的一系列低分辨率圖像，若在圖像重建過程中仍按理想位置進行重建，這會導致頻譜信息的失真，進而影響重建圖像的振幅和相位信息。圖2（b1）～（b3）分別為相機位置失配時捕獲的中心低分辨率圖像，以及重建后的振幅和相位信息，可以看出，圖2（b2）和（b3）存在明顯的偽影和褶皺。從圖2 可以看出，相機位置失配會嚴重降低重建圖像質(zhì)量。因此，進行相機位置失配校準是有必要的。

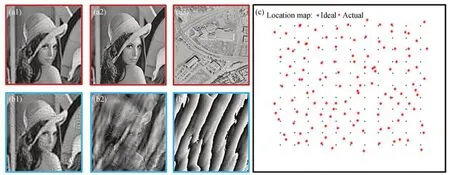
圖2 存在位置失配和不存在位置失配時傳統(tǒng)FP 的恢復結(jié)果：（a1）～（a3）相機位置未失配時捕獲的低分辨率圖像、重建圖片和相位分布；（b1）～（b3）是相機位置失配時捕獲的低分辨率圖像、重建圖片和相位分布；（c）頻譜子孔徑的位置Fig.2 Recovery results using traditional FP with positional error and without positional error.（a1）-（a3）are the captured low-resolution image，the recovered high-resolution amplitude image ，and the recovered high-resolution phase distribution without positional misalignment；（b1）-（b3）are the captured low-resolution image，the recovered high-resolution amplitude image，and the recovered high-resolution phase distribution with positional misalignment；（c）the frequency apertures’positions in the Fourier domain.

2.3 位置失配校準算法

針對遠距離成像中相機位置失配問題，本文提出了一種基于粒子群的位置失配校準算法（Correction Method Based on Particle Swarm Optimization，CPSO），實現(xiàn)相機位置失配校準功能。該算法主要對頻譜子孔徑位置進行校準，并不涉及光瞳函數(shù)的恢復，其操作流程如圖3 所示。

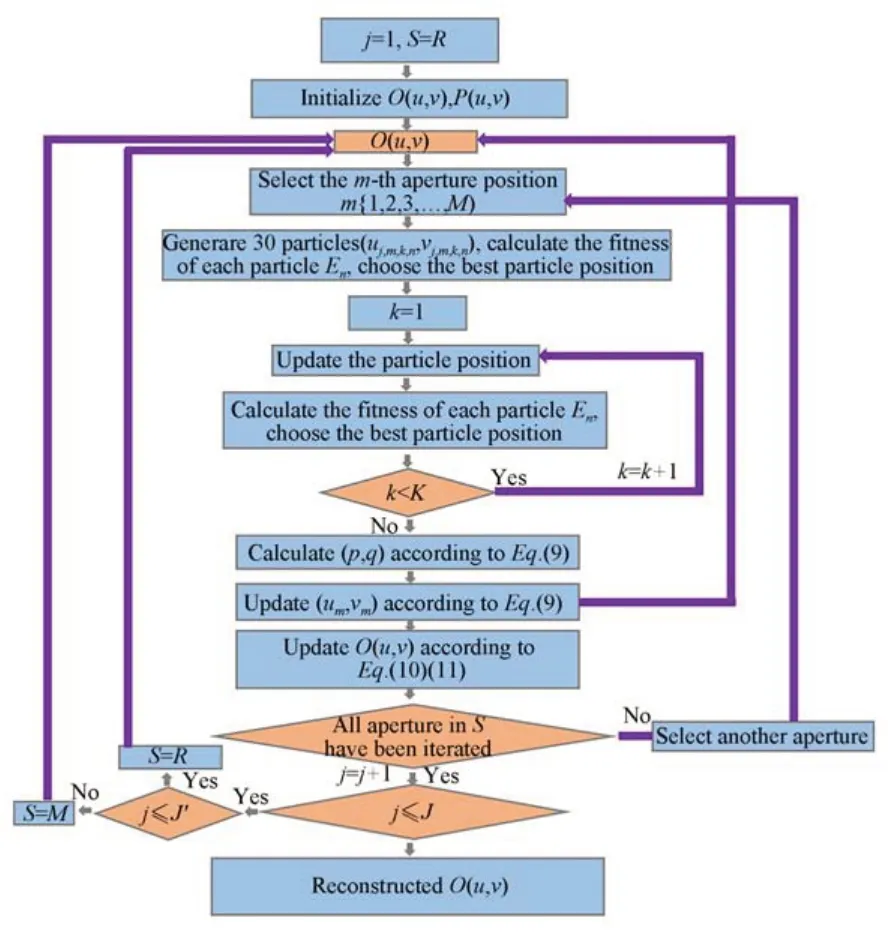
圖3 CPSO 算法流程Fig.3 Flow chart of CPSO

算法初始，通常將相機在中心位置采集的圖像插值放大后傅里葉變換至頻域，來獲取初始化頻譜估計O(u，v)，光瞳函數(shù)P(u，v)的初始化估計可視為一個圓形低通濾波器，在濾波器內(nèi)部允許頻譜信息通過，濾波器外部頻譜信息無法通過，濾波器的帶通寬度為d/(2λD)，d為相機鏡頭的等效孔徑直徑，λ為相干照明光的波長，D為樣品到相機截取平面的距離，捕獲的M張低分辨率圖像Im按設(shè)定的順序依次進行尋址，其中m∈{1，2，3，…，M}。然后，定義每輪迭代過程中需要校準的頻譜子孔徑范圍，通常情況下，根據(jù)尋址的順序逐個更新所有頻譜子區(qū)域后完成一次算法迭代，CPSO 算法共需進行J輪迭代，其中J=3。低頻信息在算法重建中起重要作用，由于對頻譜子孔徑位置采用逐個校準并更新的策略，前面頻譜子孔徑位置不夠準確，使得后續(xù)頻譜子孔徑的校準情況變差。為了提高算法的校準精度，算法初期需要對低頻信息進行校準。設(shè)定每輪圖像校準范圍為S，然后選取其中R張富含低頻信息的圖像在前J'輪進行迭代校準，校準完成后能獲取較為精確的頻譜子孔徑位置，其中R=9，J'=2。在對這R張含有物體不同頻譜信息的低分辨率圖像進行校準后，M張低分辨率圖像全部輸入算法進行1 輪迭代校準，獲取精確的頻譜子孔徑位置，其中M=121。

確定每輪迭代校準范圍后，通過粒子群算法按設(shè)定的順序逐個對頻譜子孔徑位置進行尋優(yōu)，設(shè)定單點校準時粒子的最大迭代更新次數(shù)為K，在頻譜子孔徑的理想位置(um，vm)周圍撒下N個粒子 ，每個粒子代表不同的頻移(Δuj，m，k，n，Δvj，m，k，n)，其中j∈{1，2，3}，k∈{1，2，3，…，K}，n∈{1，2，3，…，N}，(Δuj，m，k，n，Δvj，m，k，n) 表示相機失配時搜索范圍中的隨機數(shù)值。使用第n個粒子攜帶的失配參數(shù)獲取的頻域子孔徑信息為：

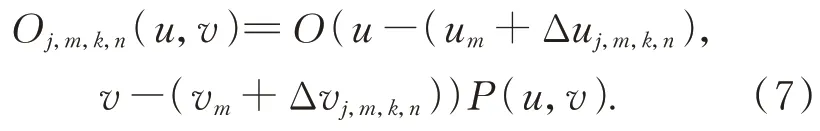
然后，將獲取的頻譜子孔徑信息逆傅里葉變換至空域，獲取低分辨率圖像估計：Oj，m，k，n(x，y)=F-1{Oj，m，k，n(u，v)}。計算低分辨率圖像估計的振幅信息|Oj，m，k，n(x，y)|與實際捕獲圖像的振幅信息之間的差值：

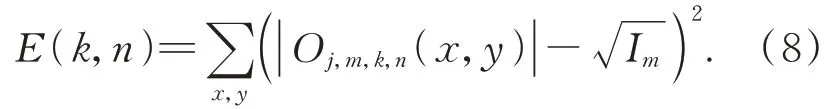
E(k，n)越小則校準后頻譜子孔徑位置越接近于實際位置。將N個粒子對應的E(k，n)值進行比較，選出最佳粒子位置，然后更新這N個粒子的位置，重復上述步驟，直至粒子位置更新次數(shù)達到預設(shè)值K。記使E(k，n)取值最小的粒子索引為(p，q)，對頻譜子孔徑位置的更新可以表示為：

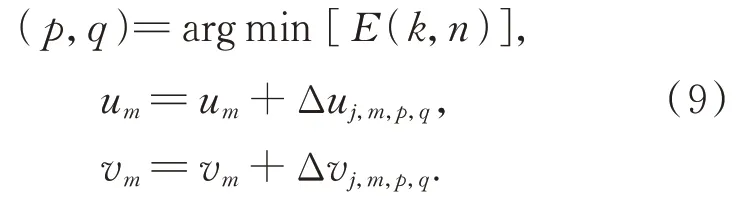
更新頻譜子孔徑位置后，獲取對應位置的頻譜信息并逆傅里葉變換至空域可得Oj，m，p，q(x，y)，用代替其振幅后再次傅里葉變換至頻域可得：

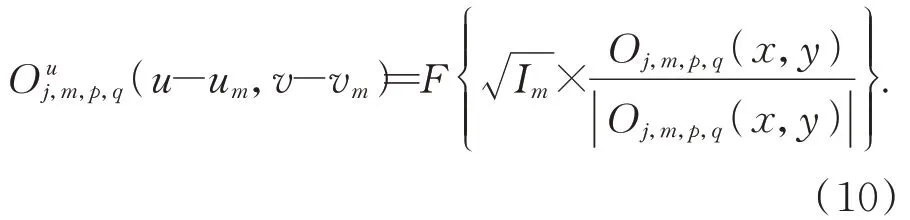
然后對頻譜進行更新，更新公式如下：

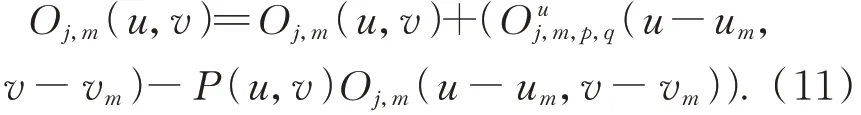
當前頻譜子孔徑位置校準并完成頻譜更新后，重復上述步驟（m=1，2，3…M），直至需要校準的頻譜子孔徑位置全部校準完畢，完成一次迭代更新。當算法完成全部J輪迭代后，頻譜子孔徑位置全部校準完畢，最后通過相位恢復算法進行迭代重建出高分辨率圖像。

3 實 驗

3.1 仿真與分析

為了證明提出的算法是有效的，首先進行仿真實驗對算法性能進行評估。由于所提算法采用逐個校準頻譜子孔徑位置的策略，且在校準完畢后更新頻譜，所以較高的孔徑重疊率［28］更有利于算法的運行。在仿真實驗中，將隨機位置偏差(Δum，Δvm)的取值設(shè)置為（-10，10），相干光波長λ是532.8 nm，成像透鏡的孔徑直徑為2.5 mm，焦距為75 mm，相機孔徑平面到樣品的距離z=1.5 m，相機傳感器的像元尺寸為3.8 μm。一個11×11 的網(wǎng)格狀位置分布代表采集低分辨率圖像時相機所在的位置，每一次相機平移0.7 mm，直至遍歷所有預設(shè)位置獲取121 幅低分辨率圖像（300×300 pixel），此時孔徑重疊率為72%，合成孔徑尺寸為9.5 mm。在本文中，根據(jù)經(jīng)驗將初始化種群大小設(shè)為30，粒子迭代更新次數(shù)設(shè)為10。

為了比較不同算法的性能，在模擬數(shù)據(jù)集上對傳 統(tǒng)FP［3］，pcPIE［17］，BF+SC［21］和CPSO 算 法進行了測試。測試集由圖4（a1）～4（a2）所示的理想高分辨率振幅圖和相位圖，經(jīng)過正向成像模型后生成的121 張低分辨率圖像組成，以此來模擬實際過程中相機捕獲的低分辨率圖像。圖4 展示了不同校準算法的仿真結(jié)果，傳統(tǒng)FP 算法的重建結(jié)果如圖4（b1）～4（b3）所示，分別為迭代重建后的高分辨率振幅圖、相位圖和頻譜圖。圖4（b1）中存在十分明顯的偽影，而圖4（b2）中存在明顯的相位起伏，重建圖像質(zhì)量相對較差。圖4（c1）～4（c3）分別為pcPIE 校準方法重建的高分辨率振幅圖、相位圖和頻譜圖，重建圖像質(zhì)量顯著提高。圖4（d1）～4（d3）為BF+SC 方法重建的高分辨率振幅圖、相位圖和頻譜圖，與傳統(tǒng)FP方法相比，重建圖像質(zhì)量同樣顯著提升。圖4（e1）～4（e3）為CPSO 方法重建的高分辨率振幅圖、相位圖和頻譜圖，重建結(jié)果與理想振幅圖和相位圖基本相同。

圖4 不同校正方法的仿真結(jié)果。（a1）理想高分辨率振幅圖；（a2）理想高分辨率相位圖；（b1）～（b3）傳統(tǒng)FP 方法；（c1）～（c3）pcPIE 方法；（d1）～（d3）BF+SC 方法；（e1）～（e3）CPSO 方法Fig.4 Simulation results of different correction methods.（a1）Ideal high-resolution amplitude image；（a2）Ideal high-resolution phase image；（b1）-（b3）Traditional FP method；（c1）-（c3）pcPIE method；（d1）-（d3）BF+SC method；（e1）-（e3）CPSO method

圖5（a）為pcPIE 算法校準后實際位置與校準位置示意圖，可以看出，大多數(shù)頻譜子孔徑位置都得到了有效校準，但由于pcPIE 算法容易陷入到局部最優(yōu)值，一些頻譜子孔徑校準后的位置與實際位置并不能完全重合，仍存在一定偏移。圖5（b）為BF+SC 算法校準后頻譜子孔徑的實際位置與理想位置示意圖，由于該算法更適用于明場圖像較多的情景中，在該模擬數(shù)據(jù)集中僅識別出9 張明場圖像，失配位置校準情況沒有獲得明顯的改善。圖5（c）為CPSO 算法校準后頻譜子孔徑的實際位置與理想位置示意圖，圓圈代表校準后的位置，可以看出實際位置與理想位置在大多數(shù)地方完全重合。值得注意的是，這3 幅圖中理想位置和實際位置分布完全相同。

圖5 相同失配條件下不同方法的校準結(jié)果Fig.5 Recover apertures’positions of different methods in same misalignment condition

為了客觀地評價不同算法的性能，引入峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）和結(jié)構(gòu)相似性（Structural Similarity Measure，SSIM）這兩個圖像質(zhì)量評價指標對不同算法的重建結(jié)果進行客觀評價，并記錄不同算法的運行時間。

不同算法重建結(jié)果的客觀評價如表1 所示。可以看出，未校準時頻譜子孔徑位置與實際頻譜子孔徑位置的像素差之和Δp為1 160，pcPIE 算法校準后的位置與實際位置像素差值之和為167，BF+SC 算法和CPSO 算法校準后的位置與實際位置像素差之和分別為159 和69。這表明相比傳統(tǒng)FP 算法，對相機失配位置進行校準能有效提高重建圖像質(zhì)量，CPSO 算法的校準效果最 佳。同 時，CPSO 算 法 的PSNR 和SSIM 值 均較高，算法運行耗時最短，這進一步表明CPSO算法能有效提升重建圖像質(zhì)量以及校準精度，并提高相機位置的校準效率。

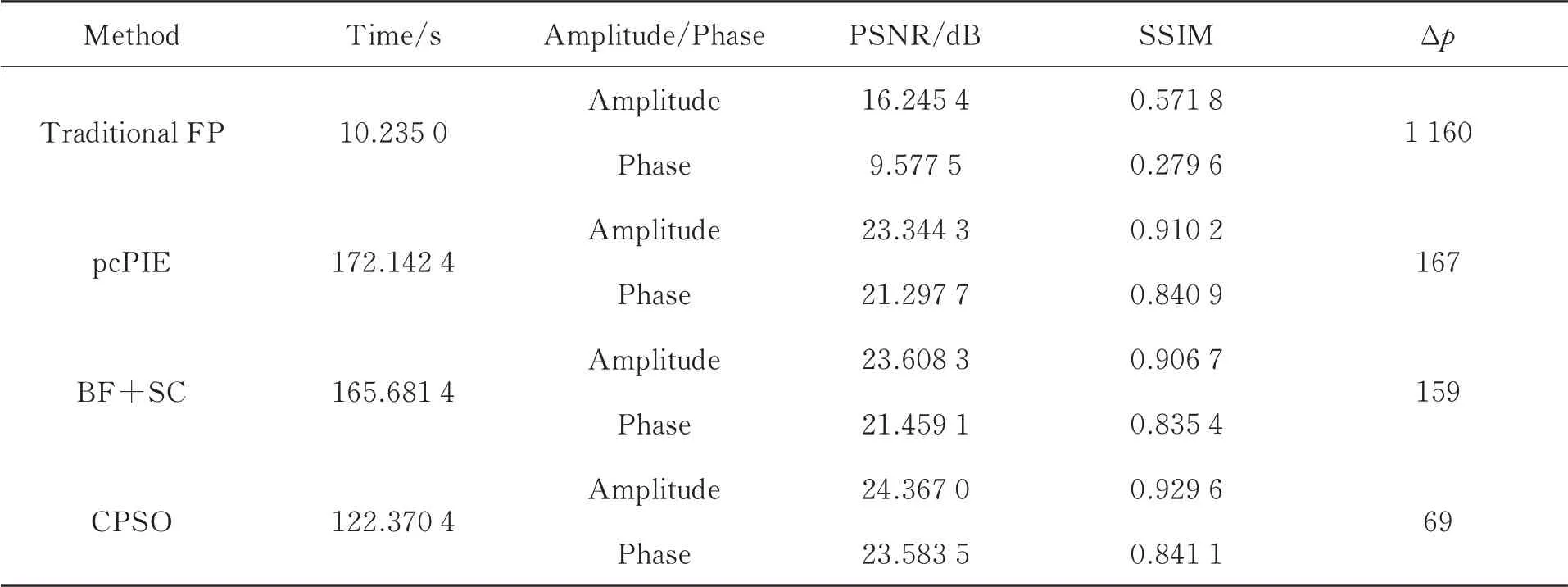
表1 不同校準算法下重建振幅圖與相位圖的客觀評價結(jié)果Tab.1 Objective evaluation results of reconstructed amplitude and phase images with different methods

為了體現(xiàn)算法的魯棒性，將分辨率板作為原始圖像再次進行仿真。除了相機位置偏移量不同，其他設(shè)置均和上文相同。不同算法的重建結(jié)果如圖6 所示，可以看出，對相機位置進行失配校準能有效減少重建圖像偽影，提升重建圖像質(zhì)量。不同方法校準后的實際位置與理想位置分布如圖7 所示。為了客觀評價不同方法重建圖像的質(zhì)量，仍然采用PSNR 和SSIM 作為重建圖像質(zhì)量指標，從表2 中可以看出，所提算法在各方面 具有一定優(yōu)勢。

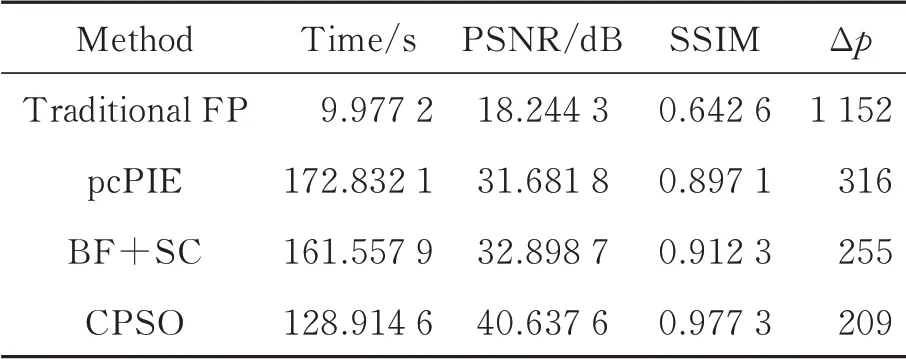
表2 不同校準算法下重建振幅圖像的客觀評價結(jié)果Tab.2 Objective evaluation results of reconstructed amplitude images with different methods

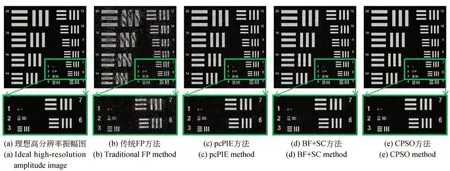
圖6 分辨率板仿真結(jié)果Fig.6 Simulation results for resolution chart

圖7 相同失配條件下不同方法的校準結(jié)果Fig.7 Recover apertures’positions of different methods in same misalignment condition

3.2 實驗與分析

為了評估算法在實際場景數(shù)據(jù)中的性能，采用Wu 團隊［29］的開源實驗數(shù)據(jù)集對算法進行驗證。該數(shù)據(jù)集由49 張含有物品不同空間頻率信息的低分辨率圖像組成。光學成像系統(tǒng)的主動照明光源為532 nm 的相干光，USAF 分辨率板到成像系統(tǒng)的距離為1.5 m，鏡頭為75 mm 焦距透鏡，像素尺寸為3.8 μm，光學系統(tǒng)的等效透鏡直徑為2 mm，相機孔徑間距為1 mm，最終合成孔徑尺寸為8 mm。圖8 為不同算法對USAF 分辨率板的重建結(jié)果。圖8（a）是相機位于中心位置時捕獲的低分辨率圖像，從圖中可以看出，第2 組元素無法識別。圖8（b）是傳統(tǒng)FP 重建的高分辨率圖像，圖像質(zhì)量較差，只能清晰分辨出第2 組元素1 的線對（4 lp/mm），第2 組元素3（方框部分，5.04 lp/mm）的水平線對和豎直線對均不易辨別。圖8（c）是pcPIE 方法的重建結(jié)果，可以看出，pcPIE 方法校準后第2 組元素2 的豎直線對難以分辨，僅能分辨出第2 組元素3 的豎直線對，水平線對無法分辨。圖8（d）和8（e）分別是BF+SC 和CPSO 算法重建的高分辨率圖像，與pcPIE方法相比，第2 組元素2 的豎直線對均能清楚分辨，但只有CPSO方法能分辨第2組元素3的水平線對，從而進一步表明所提算法性能優(yōu)于已有算法。

圖8 實驗數(shù)據(jù)集上不同算法的重建結(jié)果Fig.8 Reconstruction results of different algorithms using experiment data sets

為了對不同校準方法重建后的結(jié)果進行客觀的評估，在重建圖像上選取一條垂直于線對的紅線，獲取對應的像素分布曲線，如圖9 所示，橫軸表示紅線部分垂直向下的軌跡，縱軸表示線軌跡上的像素值。從圖中可以看出，CPSO 方法對應曲線存在3 個峰值，強度一致，且分布均勻，明顯優(yōu)于傳統(tǒng)FP，pcPIE 和BF+SC 方法。這表明獲取高分辨率圖像時無需事先對相機位置進行精密的機械校正，CPSO 算法可以解決遠距離FP對相機掃描位置精度嚴苛的需求。最后，針對不同算法的耗時進行了對比，結(jié)果如表3 所示。傳統(tǒng)FP 算法的重建速度最快，但頻譜收斂錯誤；CPSO 算法重建圖像質(zhì)量最佳，算法消耗時間相比同類校準算法減少10.9%以上。

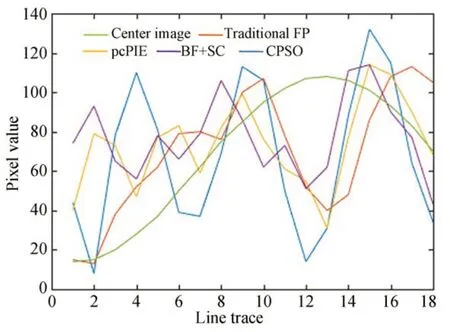
圖9 重建圖像中紅線的像素分布曲線Fig.9 Pixel distribution curve of red lines in reconstructed images

表3 不同算法的運行時間Tab.3 Running time of different methods

4 結(jié) 論

本文針對宏觀疊層成像中相機位置失配問題，提出了CPSO 算法。首先對部分低分辨率圖像進行多輪迭代校準，獲取較為精確的頻譜子孔徑位置，然后對所有低分辨率圖像進行迭代校準即可獲取每個頻譜子孔徑的精確位置，最終通過相位恢復算法重建出高分辨率圖像。實驗和仿真結(jié)果表明，與已有算法相比，CPSO 算法的重建圖像質(zhì)量和運行效率更高。盡管所提方法能有效解決相機位置失配問題，放松裝調(diào)精度要求，但當需要校準的低分辨率圖像較多時，該算法的時間成本依然較高，因此降低時間成本是今后的研究重點。